Mécanique 2 (PCSI)/Loi du moment cinétique : Pendule pesant

Début de la boite de navigation du chapitre

fin de la boite de navigation du chapitre

Nous nous plaçons, dans ce chapitre, dans le cadre de la dynamique newtonienne,
l'espace physique considéré étant $\;{\big (}$sauf avis contraire${\big )}\;$ « orienté à droite ».

Présentation du pendule pesant (non amorti) « P.P.(N.A.) »

Liaison sphérique

     On appelle « pendule pesant » tout solide placé dans un « champ de pesanteur uniforme $\;{\vec {g}}\;$» et pouvant tourner autour d’un « point fixe $\;O\;$ autre que son C.D.I. $\;G\;$», le solide étant

• en « liaison sphérique » « idéale » $\;{\big (}$voir ci-contre un schéma de principe en perspective${\big )}$, $\;{\big [}$ci-dessous la représentation symbolique d'une liaison sphérique avec précision des degrés de translation «$\;T_{i}\;$» bloqués et de ceux de rotation «$\;R_{i}\;$» libres, les forces réactives que la rotule exerce sur le pendule pesant pouvant être modélisées, dans le cas d'une liaison idéale, par une force $\;{\vec {R}}$, appliquée en $\;O\;$ et appelée « réaction de la rotule », de direction a priori quelconque dépendant des autres forces extérieures exercées sur le pendule${\big ]}$

Rotule de centre O		Liaisons : $\;\left\lbrace {\begin{array}{c}T_{x}=0\\T_{y}=0\\T_{z}=0\end{array}}\right\rbrace \;$	Libertés : $\;\left\lbrace {\begin{array}{c}R_{x}\neq 0\\R_{y}\neq 0\\R_{z}\neq 0\end{array}}\right\rbrace \;$

ou

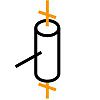
• en « liaison pivot avec le point $\;O\;$», « idéale » $\;{\big [}$ci-dessous les représentations symboliques de face, de profil et en perspective d'une liaison pivot avec précision des $\;5\;$ degrés bloqués, les $\;3\;$ degrés de translation «$\;T_{i}\;$» et $\;2\;$ des $\;3\;$ degrés de rotation «$\;R_{k}\;$», le 3^ème étant libre, les forces réactives que le pivot exerce sur le pendule pesant pouvant être modélisées, dans le cas d'une liaison idéale, par la composition d'une force $\;{\vec {R}}$, appliquée en $\;O$, appelée « réaction du pivot », de direction a priori quelconque et d'un couple de moment vectoriel $\;{\vec {\Gamma }}\;$ de direction $\;\perp \;$ à l'axe du pivot, appelé « couple de réaction du pivot », tous deux dépendant de la disposition des autres forces extérieures exercées sur le pendule${\big ]}$.

Pivot d'axe (O,x)				Liaisons : $\;\left\lbrace {\begin{array}{c}T_{x}=0\\T_{y}=0\\T_{Z}=0\\R_{y}=0\\R_{z}=0\end{array}}\right\rbrace \;$	Libertés : $\;R_{x}\neq 0\;$

     Le pendule pesant est dit « non amorti » si on néglige toute force de frottement fluide ;

     on note «$\;m\;$» la masse du pendule, «$\;{\mathfrak {a}}\;$» la distance séparant le C.D.I. $\;G\;$ du pendule de son point $\;O\;$ fixe dans le référentiel d'étude $\;{\mathcal {R}}$, référentiel dans lequel on repère le pendule par l’intermédiaire des coordonnées de son C.D.I. «$\;G\;$» $\;{\big [}$le meilleur repérage dans le cas d'une liaison sphérique serait le repérage sphérique de pôle $\;O\;$ et d'axe $\;{\overrightarrow {Oz}}\;$ vertical descendant mais, avec ce choix, la difficulté apparaîtrait dès lors que l'on aurait besoin de former des dérivées temporelles secondes des vecteurs de base d'où le rejet de ce choix au profit du repérage le plus proche c'est-à-dire le repérage cylindro-polaire d'axe $\;{\overrightarrow {Oz}}\;$ vertical descendant$\;\ldots {\big ]}$ ;

     avec le repérage cylindro-polaire d'axe $\;{\overrightarrow {Oz}}\;$ vertical descendant de l'espace physique « orienté à droite » $\;{\big [}$il conviendrait bien sûr d’ajouter un schéma de situation${\big ]}$,

• tout point $\;M\;$ du pendule pesant a pour coordonnées cylindro-polaires «$\;\left(\rho \,,\,\varphi \,,\,z\right)\;$» dans la base locale associée $\;{\big (}$orthonormée directe${\big )}\;$ «$\;\left({\vec {u}}_{\rho }\,,\,{\vec {u}}_{\varphi }\,,\,{\vec {u}}_{z}\right)\;$» et
• le C.D.I. $\;G\;$ du pendule pesant, pour coordonnées cylindro-polaires «$\;\left(\rho _{G}\,,\,\varphi _{G}\,,\,z_{G}\right)\;$» dans la base locale associée $\;{\big (}$orthonormée directe${\big )}\;$ «$\;\left({\vec {u}}_{\rho _{G}}\,,\,{\vec {u}}_{\varphi _{G}}\,,\,{\vec {u}}_{z}\right)\;$».

Conditions initiales (C.I.) de lancement pour que le mouvement du pendule pesant (non amorti) (P.P.(N.A.)) soit à un degré de liberté, établissement de la nature « rotatoire » de son mouvement

C.I. de lancement pour que le mouvement du P.P.(N.A.) soit à un degré de liberté

     Les C.I. de lancement du P.P.(N.A.) dépendent du type de liaison existant entre le solide et le point fixe $\;O$ ;

• s’il s’agit d’une liaison sphérique pour laquelle existent trois degrés de liberté de rotation, les C.I. de lancement sont les suivantes :
  $\;\succ \;$« on écarte le P.P.(N.A.) de sa position d’équilibre stable $\;{\big (}$correspondant à $\;G\;$ sur la verticale de $\;O\;$ et au-dessous${\big )}\;$ et on le lâche sans vitesse initiale $\;\left(C.I.\;{\mathfrak {a}}\right)\;$» ou
  $\;\succ \;$« on écarte le P.P.(N.A.) de sa position d’équilibre stable $\;{\big (}$correspondant à $\;G\;$ sur la verticale de $\;O\;$ et au-dessous${\big )}\;$ et on le lâche avec une vitesse initiale de son C.D.I. située dans le plan vertical contenant $\;O\;\left(C.I.\;{\mathfrak {b}}\right)\;$» ;

• s’il s’agit d’une liaison pivot, celle-ci imposant un seul degré de liberté de rotation, les C.I. de lancement peuvent être quelconques $\;{\big [}$toutefois la liaison n'autorise qu'une vitesse initiale de lancement $\;\perp \;$ à l'axe de la liaison${\big ]}$.

Dans le cas d’une liaison sphérique et avec les C.I. de lancement (C.I. a) ou (C.I. b), établissement de la nature plane du mouvement du C.D.I. G du P.P.(N.A.)

Schéma d'un P.P.(N.A.) à liaison sphérique avec ajout des actions extérieures, repérage cylindro-polaire d'axe $\;{\overrightarrow {Oz}}\;$ vertical descendant du C.D.I. $\;G\;$ du pendule

     La démonstration est analogue à celle exposée pour établir la nature plane du mouvement du P.P.S.(N.A.) lancé dans les C.I. «$\;1a\;$» ou «$\;1b\;$» dans le paragraphe « démonstration de la nature plane du mouvement de M dans les C.I. de lancement 1a (ou 1b) » du chap.$12$ de la leçon « Mécanique 1 (PCSI) », toutefois, nécessitant de légères modifications, elle est exposée ci-dessous :

     les seules actions extérieures exercées sur le pendule sont $\;{\big (}$voir schéma ci-contre${\big )}$

• son poids «$\;m\;{\vec {g}}=m\;g\;{\vec {u}}_{z}\;$» de moment vectoriel par rapport à $\;O\;$ «$\;{\overrightarrow {\mathcal {M}}}_{\!O}\!\left[m\;{\vec {g}}\right](t)={\overrightarrow {OG}}(t)\wedge m\;{\vec {g}}={\mathfrak {a}}\;{\vec {u}}_{r_{G}}(t)\wedge m\;{\vec {g}}\;$» dans lequel $\;{\vec {u}}_{r_{G}}(t)=$ $\sin \!\left[\theta _{G}(t)\right]\,{\vec {u}}_{\rho _{G}}(t)+\cos \!\left[\theta _{G}(t)\right]\,{\vec {u}}_{z}\;$ $\Rightarrow$ $\;{\overrightarrow {\mathcal {M}}}_{\!O}\!\left[m\;{\vec {g}}\right](t)={\mathfrak {a}}\,\left\lbrace \sin \!\left[\theta _{G}(t)\right]\,{\vec {u}}_{\rho _{G}}(t)+\cos \!\left[\theta _{G}(t)\right]\,{\vec {u}}_{z}\right\rbrace \wedge m\;g\;{\vec {u}}_{z}\;$ ou, en utilisant la distributivité de la multiplication par un scalaire d'une part ainsi que la distributivité de la multiplication vectorielle relativement à l'addition vectorielle d'autre part $\;{\overrightarrow {\mathcal {M}}}_{\!O}\!\left[m\;{\vec {g}}\right](t)=$ ${\mathfrak {a}}\;\sin \!\left[\theta _{G}(t)\right]\,{\vec {u}}_{\rho _{G}}(t)\wedge m\;g\;{\vec {u}}_{z}\;{\cancel {+\;{\mathfrak {a}}\;\cos \!\left[\theta _{G}(t)\right]\,{\vec {u}}_{z}\wedge m\;g\;{\vec {u}}_{z}}}\;$ soit «$\;{\overrightarrow {\mathcal {M}}}_{\!O}\!\left[m\;{\vec {g}}\right](t)=$ $-m\;g\;{\mathfrak {a}}\;\sin \!\left[\theta _{G}(t)\right]\;{\vec {u}}_{\varphi _{G}}(t)\;$» et
• les actions de la liaison sphérique en $\;O\;$ se réduisant à « la réaction $\;{\vec {R}}(t)=R_{\rho _{G}}(t)\;{\vec {u}}_{\rho _{G}}(t)+R_{\varphi _{G}}(t)\;{\vec {u}}_{\varphi _{G}}(t)+R_{z}(t)\;{\vec {u}}_{z}\;$ appliquée en $\;O\;$» de vecteur moment par rapport à $\;O\;$ «$\;{\overrightarrow {\mathcal {M}}}_{\!O}\!\left[{\vec {R}}(t)\right]={\vec {0}}\;$».

     Démonstration de la nature plane du mouvement de $\;G\;$ dans les $\;\left(C.I.\;{\mathfrak {a}}\right)\;$ de lancement : le théorème du mouvement du C.D.I. appliqué au pendule pesant dans le référentiel terrestre galiléen $\;m\;{\vec {g}}+{\vec {R}}(t)=m\;{\vec {a}}_{G}(t)\;$ projeté sur $\;{\vec {u}}_{\varphi _{G}}\;$ nous conduit à «$\;m\;g_{\varphi _{G}}+R_{\varphi _{G}}(t)=$ $m\;a_{\varphi _{G},\,G}(t)\;$» ou, les composantes de $\;{\vec {g}}\;$ et de $\;{\vec {R}}(t)\;$ sur $\;{\vec {u}}_{\varphi _{G}}(t)\;$ étant nulles $\;{\big [}$car $\;{\vec {u}}_{\varphi _{G}}(t)\;$ est $\;\perp \;$ au plan vertical contenant $\;{\overrightarrow {OG}}(t)\;$ donc $\;\perp \;$ à $\;{\vec {g}}\;$ et à $\;{\vec {R}}(t){\big ]}\;$ on obtient, après simplification par $\;m$,

«$\;a_{\varphi _{G},\,G}(t)=0,\;\;\forall \;t\in \mathbb {R} ^{+}\;$» ou,

     Démonstration de la nature plane du mouvement de $\;\color {transparent}{G}\;$ dans les $\;\color {transparent}{\left(C.I.\;{\mathfrak {a}}\right)}\;$ de lancement : pour les valeurs de $\;t\;$ telles que $\;\rho _{G}(t)\neq 0$ $\;{\big [}$c'est-à-dire $\;t\neq t_{\text{éq stable}}\;$ instants de passage par la position verticale d'équilibre stable du P.P. pour lesquels $\;\theta (t_{\text{éq stable}})=0\;$ et donc $\;\rho _{G}(t_{\text{éq stable}})=0{\big ]}$, en utilisant la forme « semi intégrée » de l'accélération orthoradiale «$\;a_{\varphi _{G},\,G}(t)={\dfrac {1}{\rho _{G}(t)}}\;{\dfrac {d\!\left[\rho _{G}^{2}\,{\dot {\varphi _{G}}}\right]}{dt}}(t)\;$» et après simplification par $\;{\dfrac {1}{\rho _{G}(t)}}\neq 0,\;\;\forall \;t$, l'équation différentielle suivante

«$\;{\dfrac {d\!\left[\rho _{G}^{2}\,{\dot {\varphi _{G}}}\right]}{dt}}(t)=0\;$ pour $\;t\in \mathbb {R} ^{+}\setminus \left\lbrace t_{\text{éq stable}}\right\rbrace \;$»,

     Démonstration de la nature plane du mouvement de $\;\color {transparent}{G}\;$ dans les $\;\color {transparent}{\left(C.I.\;{\mathfrak {a}}\right)}\;$ de lancement : qui s'intègre, sur chaque intervalle continu de temps ne contenant pas de valeurs $\;t_{\text{éq stable}}$, en

$\;\rho _{G}^{2}(t)\,{\dot {\varphi _{G}}}(t)=cste\;$ et

     Démonstration de la nature plane du mouvement de $\;\color {transparent}{G}\;$ dans les $\;\color {transparent}{\left(C.I.\;{\mathfrak {a}}\right)}\;$ de lancement : dont on peut prolonger le résultat aux valeurs discrètes $\;t_{\text{éq stable}}\;$ compte-tenu de la continuité des grandeurs $\;\rho _{G}(t)\;$ et $\;{\dot {\varphi _{G}}}(t)\;$ pour tout $\;t\in \mathbb {R}$, ce qui entraîne la continuité de $\;\rho _{G}^{2}(t)\,{\dot {\varphi _{G}}}(t)\;$ soit finalement

«$\;\rho _{G}^{2}(t)\,{\dot {\varphi _{G}}}(t)=cste,\;\;\forall \;t\in \mathbb {R} ^{+}\;$» ;

     Démonstration de la nature plane du mouvement de $\;\color {transparent}{G}\;$ dans les $\;\color {transparent}{\left(C.I.\;{\mathfrak {a}}\right)}\;$ de lancement : on détermine la constante $\;cste\;$ par utilisation partielle des C.I. $\;\left\lbrace {\begin{array}{l}\theta _{G}(0)=\theta _{0}\;&{\text{et }}&\varphi _{G}(0)=0\\{\dot {\theta _{G}}}(0)=0\;&{\text{et }}&{\dot {\varphi _{G}}}(0)=0\end{array}}\right\rbrace \;$ soit, avec «$\;\rho _{G}(t)={\mathfrak {a}}\;\sin \!\left[\theta _{G}(t)\right]\;$», la réécriture partielle des C.I. sous la forme «$\;{\mathfrak {a}}^{2}\;\sin ^{2}(\theta _{0})\;{\dot {\varphi _{G}}}(0)=cste\;$» ou «$\;0=cste\;$» et par suite

«$\;\rho _{G}^{2}(t)\,{\dot {\varphi _{G}}}(t)=0,\;\;\forall \;t\in \mathbb {R} ^{+}\;$» ou,

     Démonstration de la nature plane du mouvement de $\;\color {transparent}{G}\;$ dans les $\;\color {transparent}{\left(C.I.\;{\mathfrak {a}}\right)}\;$ de lancement : en simplifiant par $\;\rho _{G}^{2}(t)\;$ non identiquement nul,

«$\;{\dot {\varphi _{G}}}(t)=0,\;\;\forall \;t\in \mathbb {R} ^{+}\;$» ou enfin,

     Démonstration de la nature plane du mouvement de $\;\color {transparent}{G}\;$ dans les $\;\color {transparent}{\left(C.I.\;{\mathfrak {a}}\right)}\;$ de lancement : après intégration «$\;\varphi _{G}(t)=cste',\;\;\forall \;t\in \mathbb {R} ^{+}\;$», valeur de $\;cste'\;$ déterminée par C.I. $\;\varphi _{G}(0)=0$, soit

«$\;\varphi _{G}(t)=0,\;\;\forall \;t\in \mathbb {R} ^{+}\;$»,
c'est-à-dire la nature plane du mouvement de $\;G\;$ dans le plan de lancement.

     Démonstration de la nature plane du mouvement de $\;G\;$ dans les $\;\left(C.I.\;{\mathfrak {b}}\right)\;$ de lancement : aucune modification avant l'intervention des C.I. c'est-à-dire qu'on établit «$\;\rho ^{2}(t)\,{\dot {\varphi }}(t)=cste,\;\;\forall \;t\in \mathbb {R} ^{+}\;$» comme précédemment, la constante $\;cste\;$ se déterminant par utilisation partielle des C.I. $\;\left\lbrace {\begin{array}{l}\theta _{G}(0)=\theta _{0}\;&{\text{et }}&\varphi _{G}(0)=0\\{\dot {\theta _{G}}}(0)={\dfrac {V_{0}}{\mathfrak {a}}}\;&{\text{et }}&{\dot {\varphi _{G}}}(0)=0\end{array}}\right\rbrace \;$ soit, avec «$\;\rho _{G}(t)={\mathfrak {a}}\;\sin \!\left[\theta _{G}(t)\right]\;$», la réécriture partielle des C.I. sous la forme «$\;{\mathfrak {a}}^{2}\;\sin ^{2}(\theta _{0})\;{\dot {\varphi _{G}}}(0)=cste\;$» ou «$\;0=cste\;$» et par suite

«$\;\rho _{G}^{2}(t)\,{\dot {\varphi _{G}}}(t)=0,\;\;\forall \;t\in \mathbb {R} ^{+}\;$» ou,

     Démonstration de la nature plane du mouvement de $\;\color {transparent}{G}\;$ dans les $\;\color {transparent}{\left(C.I.\;{\mathfrak {b}}\right)}\;$ de lancement : en simplifiant par $\;\rho _{G}^{2}(t)\;$ non identiquement nul,

«$\;{\dot {\varphi _{G}}}(t)=0,\;\;\forall \;t\in \mathbb {R} ^{+}\;$» ou enfin,

     Démonstration de la nature plane du mouvement de $\;\color {transparent}{G}\;$ dans les $\;\color {transparent}{\left(C.I.\;{\mathfrak {b}}\right)}\;$ de lancement : après intégration «$\;\varphi _{G}(t)=cste',\;\;\forall \;t\in \mathbb {R} ^{+}\;$», valeur de $\;cste'\;$ déterminée par C.I. $\;\varphi _{G}(0)=0$, soit

«$\;\varphi _{G}(t)=0,\;\;\forall \;t\in \mathbb {R} ^{+}\;$»,
c'est-à-dire la nature plane du mouvement de $\;G\;$ dans le plan de lancement.

Dans le cas d’une « liaison pivot » ou d’une « liaison sphérique avec C.I. de lancement (C.I. a) ou (C.I. b) », nouveau repérage adapté à la nature rotatoire du mouvement du P.P.(N.A.) à un degré de liberté

Schéma d'un pendule pesant non amorti à un degré de liberté, repérage polaire de son C.D.I. $\;G\;$ et représentation des forces extérieures

     Avec les deux types de liaison, « liaison pivot » ou « liaison sphérique avec C.I. de lancement $\;\left(C.I.\;{\mathfrak {a}}\right)\;$ ou $\;\left(C.I.\;{\mathfrak {b}}\right)\;$», le P.P.(N.A.) ayant un mouvement de rotation autour d’un axe horizontal fixe noté $\;\Delta _{O}\;$ et orienté par «$\;{\vec {u}}_{\Delta _{O}}\;$»,
     on repère le C.D.I. $\;G\;$ du P.P.(N.A.) dans le plan vertical du mouvement $\;zOx$ $\;{\big \{}$avec $\;{\vec {u}}_{z}\;$ unitaire vertical descendant, $\;{\vec {u}}_{x}\;$ unitaire horizontal $\;\perp \;$ au 3^ème vecteur unitaire horizontal $\;{\vec {u}}_{y}={\vec {u}}_{\Delta _{O}}\;$ tels que la base cartésienne «$\;\left({\vec {u}}_{z}\,,\,{\vec {u}}_{x}\,,\,{\vec {u}}_{\Delta _{O}}\right)\;$ soit directe »${\big \}}$, l'espace physique étant orienté à droite,
              on repère le C.D.I. $\;\color {transparent}{G}\;$ du P.P.(N.A.) par ses coordonnées polaires de pôle $\;O\;$ et d’axe $\;\Delta _{O}\;$ orienté par $\;{\vec {u}}_{\Delta _{O}}\;$ soit, avec la base polaire liée au C.D.I. $\;G\;$ du P.P.(N.A.) dans ce plan $\;zOx$, «$\;\left({\vec {u}}_{r}\,,\,{\vec {u}}_{\theta }\right)\;$», «$\;\left\lbrace r_{G}={\mathfrak {a}}\,,\,\theta _{G}={\widehat {\left({\vec {u}}_{z}\,,\,{\overrightarrow {OG}}\right)}}={\widehat {\left({\vec {u}}_{z}\,,\,{\vec {u}}_{r}\right)}}\right\rbrace \;$», «$\;\theta _{G}\;$» $\;{\big [}$abscisse angulaire du C.D.I. $\;G\;$ du P.P.(N.A.) noté «$\;\theta \;$» par la suite en absence d'ambiguïté${\big ]}\;$ est aussi le paramètre de position angulaire utilisé pour repérer le mouvement du P.P.(N.A.).

     Les actions extérieures agissant sur le P.P.N.A. représentées sur le schéma ci-contre sont les seules dans l'hypothèse d'une « liaison sphérique avec C.I. de lancement $\;\left(C.I.\;{\mathfrak {a}}\right)\;$ ou $\;\left(C.I.\;{\mathfrak {b}}\right)\;$», mais $\;\ldots$
           Les actions extérieures agissant sur le P.P.N.A. représentées sur le schéma ci-contre sont les seules dans celle d'une « liaison pivot » il faudrait ajouter le couple de réaction du pivot de moment vectoriel $\;{\vec {\Gamma }}_{{\text{pendule}}\,\leftarrow \,{\text{pivot}}}\;\perp \;$ à $\;\Delta _{O}$ $\;{\big [}$on rappelle qu'un couple n'est pas représenté par son moment mais par le sens de rotation qu'il engendrerait s'il agissait seul en mettant, à côté de la flèche incurvée précisant le sens, le nom du vecteur moment du couple, ici ce n'est pas fait car ce couple n'interviendra pas dans l'application du théorème de la dynamique permettant d'obtenir l'équation différentielle en $\;\theta (t)\;$ du P.P.N.A.${\big ]}$.

Établissement de l’équation différentielle du mouvement du pendule pesant non amorti (à un degré de liberté) par application du théorème du moment cinétique scalaire

     $\;\Delta _{O}\;$ étant un axe fixe dans le référentiel d’étude $\;{\mathcal {R}}\;$ galiléen, on peut appliquer au P.P.N.A. à un degré de liberté le théorème du moment cinétique scalaire par rapport à l’axe $\;\Delta _{O}$, les actions extérieures s'exerçant sur le pendule étant :

• son poids «$\;m\;{\vec {g}}=m\;g\;{\vec {u}}_{z}\;$» de moment scalaire par rapport à $\;\Delta _{O}\;$ «$\;{\mathcal {M}}_{\!\Delta _{O}}\!\left[m\;{\vec {g}}\right](t)=\left[{\overrightarrow {OG}}(t)\wedge m\;{\vec {g}}\right]\cdot {\vec {u}}_{\Delta _{O}}=-m\;g\;{\mathfrak {a}}\;\sin \!\left[\theta (t)\right]\;$»,
• la réaction du point $\;O\;$ de la liaison sphérique sur le pendule lancé dans les C.I. $\;\left(C.I.\;{\mathfrak {a}}\right)\;$ ou $\;\left(C.I.\;{\mathfrak {b}}\right)$, «$\;{\vec {R}}(t)=R_{r}(t)\;{\vec {u}}_{r}(t)+R_{\theta }(t)\;{\vec {u}}_{\theta }(t)\;$» de moment scalaire «$\;{\mathcal {M}}_{\!\Delta _{O}}\!\left[{\vec {R}}(t)\right]=0\;$» ou
  la réaction de l'axe $\;\Delta _{O}\;$ de la liaison pivot sur le pendule lancé avec n'importe quelles C.I. compatibles avec la liaison, «$\;{\vec {R}}(t)=R_{r}(t)\;{\vec {u}}_{r}(t)+R_{\theta }(t)\;{\vec {u}}_{\theta }(t)\;$» de moment scalaire «$\;{\mathcal {M}}_{\!\Delta _{O}}\!\left[{\vec {R}}(t)\right]$ $=0\;$» auquel s'ajoute le couple de réaction du pivot de moment vectoriel $\;{\vec {\Gamma }}_{{\text{pendule}}\,\leftarrow \,{\text{pivot}}}={\overline {\Gamma _{{\text{pendule}}\,\leftarrow \,{\text{pivot}},\,r}}}\;{\vec {u}}_{r}+{\overline {\Gamma _{{\text{pendule}}\,\leftarrow \,{\text{pivot}},\,\theta }}}\;{\vec {u}}_{\theta }\;$ et par suite de moment scalaire relativement à $\;\Delta _{O}\;$ «$\;{\overline {\Gamma _{{\text{pendule}}\,\leftarrow \,{\text{pivot}},}}}_{\Delta _{O}}=0\;$» ;

     l'application du théorème du moment cinétique scalaire au P.P.N.A. en rotation autour de l'axe $\;\Delta _{O}$, fixe dans le référentiel d'étude $\;{\mathcal {R}}\;$ galiléen, avec la vitesse angulaire $\;{\dot {\theta }}(t)\;$ à l'instant $\;t$, s'écrit

«$\;{\mathcal {M}}_{\!\Delta _{O}}\!\left[m\;{\vec {g}}\right](t)+{\mathcal {M}}_{\!\Delta _{O}}\!\left[{\vec {R}}(t)\right]=J_{\Delta _{O}}\;{\ddot {\theta }}(t)\;$» dans le cas d'un P.P.N.A. à un degré de liberté, lié à $\;O\;$ par « liaison sphérique » ou
«$\;{\mathcal {M}}_{\!\Delta _{O}}\!\left[m\;{\vec {g}}\right](t)+{\mathcal {M}}_{\!\Delta _{O}}\!\left[{\vec {R}}(t)\right]+{\overline {\Gamma _{{\text{pendule}}\,\leftarrow \,{\text{pivot}},}}}_{\Delta _{O}}=J_{\Delta _{O}}\;{\ddot {\theta }}(t)\;$» dans le cas d'un P.P.N.A. lié à $\;\Delta _{O}\;$ par « liaison pivot »,
«$\;J_{\Delta _{O}}\;$ étant le moment d'inertie du P.P.(N.A.) relativement à $\;\Delta _{O}\;$» et
«$\;{\ddot {\theta }}(t)\;$ l'accélération angulaire du P.P.(N.A.) à l'instant $\;t\;$» soit

     en remplaçant les moments scalaires par leur expression précédemment déterminée,

«$\;-m\;g\;{\mathfrak {a}}\;\sin \!\left[\theta (t)\right]+0=J_{\Delta _{O}}\;{\ddot {\theta }}(t)\;$» dans le cas d'un P.P.N.A. à un degré de liberté, lié à $\;O\;$ par « liaison sphérique » ou
«$\;-m\;g\;{\mathfrak {a}}\;\sin \!\left[\theta (t)\right]+0+0=J_{\Delta _{O}}\;{\ddot {\theta }}(t)\;$» dans le cas d'un P.P.N.A. lié à $\;\Delta _{O}\;$ par « liaison pivot » ou encore,

     en normalisant l'équation différentielle en $\;\theta (t)\;$ du mouvement du P.P.N.A.

«$\;{\ddot {\theta }}(t)+{\dfrac {m\;g\;{\mathfrak {a}}}{J_{\Delta _{O}}}}\;\sin \!\left[\theta (t)\right]=0\;$» soit
une équation différentielle non linéaire du 2^ème ordre en $\;\theta (t)\;$ sans terme du 1^er ordre,
caractérisant un oscillateur non linéaire dans la mesure où le mouvement reste oscillatoire.

Absence de solution analytique dans le cas général d’élongations angulaires non petites

     Comme l’équation différentielle en $\;\theta (t)\;$ du P.P.(N.A.) est de même nature que celle du « P.P.S.(N.A.)  », on peut faire les mêmes commentaires, rappelés ci-après :

     l’équation différentielle non linéaire du 2^ème ordre en $\;f(x)$ $\;{\big (}$sans terme du 1^er ordre${\big )}$ $\;{\dfrac {d^{2}f}{dx^{2}}}(x)+k\;\sin \!\left[f(x)\right]=0\;$ n'ayant pas de solution analytique on conclut à

l’absence de résolution analytique exacte de l’équation différentielle du P.P.(N.A.),

     la seule possibilité est une résolution approchée

• analytique dans le cas d’« élongations angulaires petites » $\;{\big [}$voir le paragraphe « cas particulier des petites élongations angulaires, pendule pesant (non amorti à un degré de liberté) = oscillateur harmonique (non amorti) approché de rotation, période des petites oscillations » plus loin dans le chapitre${\big ]}\;$ ou
• numérique dans le cas général d’« élongations angulaires non petites » $\;{\big [}$résolution analogue à celle présentée au paragraphe « en complément, résolution numérique de l'équation différentielle d'un P.P.S. dans les C.I. 1a puis 1b, tracé des diagrammes horaires de position et de vitesse ainsi que celui des portraits de phase correspondant » du chap.$12$ de la leçon « Mécanique 1 (PCSI) »${\big ]}$.

Cas particulier des « petites élongations angulaires », pendule pesant (non amorti à un degré de liberté) = oscillateur harmonique (non amorti) approché de rotation, période des « petites oscillations »

     Le traitement effectué dans ce paragraphe est analogue à celui présenté dans le paragraphe « approximation linéaire, dans le cadre des petites élongations angulaires, du mouvement d'un P.P.S. à un degré de liberté, analogie avec l'oscillateur harmonique, période des petites élongations angulaires » du chap.$12$ de la leçon « Mécanique 1 (PCSI) ».

Cadre des « petites élongations angulaires »

     Le plus simple pour être dans le cadre des « petites élongations angulaires » est de lancer le P.P.N.A. avec les C.I. de lancement particulières $\;{\big (}$que la liaison avec $\;O\;$ ou $\;\Delta _{O}\;$ soit sphérique ou pivot${\big )}$ suivantes :

     « on écarte le P.P.N.A. de sa position d’équilibre stable et on le lâche sans vitesse initiale » en supposant l’abscisse angulaire initiale $\;\theta _{0}\;$ de valeur absolue petite c'est-à-dire $\;\vert \theta _{0}\vert \ll 1\;$,

                « on écarte le P.P.N.A. de sa position d’équilibre stable et l'absence de vitesse angulaire initiale assurant que « la valeur absolue de l'élongation angulaire ne dépassera pas $\;\vert \theta _{0}\vert \;$» et restera petite soit

«$\;\vert \theta (t)\vert \ll 1\;\;\forall \;t\;$».

Approximation linéaire du P.P.(N.A.) dans le cadre des « petites élongations angulaires »

     Dans le cadre des « petites élongations angulaires » on a $\;\vert \theta (t)\vert \ll \;\;\forall \;t\;$ permettant d'effectuer un D.L. à l'ordre un en $\;\theta \;$ de $\;\sin(\theta )\;$ au voisinage de $\;0\;$ selon $\;\sin(\theta )\simeq \theta \;$ à l'ordre un en $\;\theta \;$ et par suite

l'équation différentielle suivie par le P.P.N.A. devient linéaire selon «$\;{\ddot {\theta }}(t)+{\dfrac {m\;g\;{\mathfrak {a}}}{J_{\Delta _{O}}}}\;\theta (t)\simeq 0\;$» c'est-à-dire
une équation différentielle linéaire à cœfficients constants du 2^ème ordre en $\;\theta (t)\;$ sans terme d'amortissement et homogène.

P.P.(N.A.) à un degré de liberté dans le cadre des « petites élongations angulaires » = oscillateur harmonique (non amorti) approché de rotation

     Le P.P.(N.A.) est donc linéarisable dans l'hypothèse des « petites élongations angulaires » et dans cette hypothèse il devient

un « oscillateur harmonique (non amorti) » de « pulsation propre $\;\omega _{0}={\sqrt {\dfrac {m\;g\;{\mathfrak {a}}}{J_{\Delta _{O}}}}}\;$»
appelée « pulsation $\;{\big (}$propre${\big )}\;$ des petites élongations angulaires ».

Période des « petites oscillations »

     On en déduit la « période propre des petites élongations angulaires du P.P.(N.A.) à un degré de liberté » «$\;{\mathcal {T}}_{0}={\dfrac {2\;\pi }{\omega _{0}}}=2\;\pi \;{\sqrt {\dfrac {J_{\Delta _{O}}}{m\;g\;{\mathfrak {a}}}}}\;$» ;

     on constate que le P.P.(N.A.) « bât plus vite », en un lieu fixé, pour «$\;{\dfrac {J_{\Delta _{O}}}{\mathfrak {a}}}\;$ plus petit » réalisé pour une répartition de masse plus proche de l’axe $\;\Delta _{O}\;$ c'est-à-dire «$\;J_{\Delta _{O}}\;$ plus petit » et

                on constate que le P.P.(N.A.) « bât plus vite », à répartition de masse fixée, pour une « intensité de pesanteur $\;g\;$ plus grande » $\;{\big [}$ainsi le P.P.N.A. sur Terre « bât un peu plus vite » aux pôles qu'à l'équateur et le même P.P.N.A. « bât nettement plus rapidement » sur la Terre (♁) que sur la Lune (☽)${\big ]}$.

Intégrale 1^ère du mouvement du pendule pesant (non amorti à un degré de liberté) dans le cas général des élongations angulaires non petites

Introduction

     La meilleure façon d’obtenir cette intégrale 1^ère du mouvement du P.P.N.A. à un degré de liberté est de faire une étude énergétique, mais les notions d’énergies d’un système discret de points matériels ou d’un système continu de matière n’étant vues qu'aux chap.$9$ « énergie cinétique d'un solide en rotation », $10$ « lois scalaires de l'énergie cinétique » et $11$ « lois de l'énergie cinétique pour un système déformable de points matériels » de la leçon « Mécanique 2 (PCSI) », nous allons procéder autrement $\;{\big \{}$la détermination directe de l’intégrale 1^ère $\;{\big [}$selon la meilleure méthode exposée dans les chapitres précités de la leçon « Mécanique 2 (PCSI) »${\big ]}\;$ sera vue dans le paragraphe « énergie mécanique du pendule pesant et sa conservation en absence de frottement » du chap.$10$ de la leçon « Mécanique 2 (PCSI) »${\big \}}$.

Détermination de l’intégrale 1^ère du mouvement du P.P.(N.A.) à partir de l’équation différentielle du mouvement en θ(t) suivi par ce dernier

     L’équation différentielle du mouvement en $\;\theta (t)\;$ du P.P.N.A. étant «$\;{\ddot {\theta }}(t)+{\dfrac {m\;g\;{\mathfrak {a}}}{J_{\Delta _{O}}}}\;\sin \!\left[\theta (t)\right]=0\;$», on multiplie celle-ci par «$\;{\dot {\theta }}(t)\;$» ce qui donne «$\;{\ddot {\theta }}(t)\;{\dot {\theta }}(t)+{\dfrac {m\;g\;{\mathfrak {a}}}{J_{\Delta _{O}}}}\;\sin \!\left[\theta (t)\right]\,{\dot {\theta }}(t)=0\;$» soit, en reconnaissant

• dans le 1^er terme «$\;{\ddot {\theta }}(t)\;{\dot {\theta }}(t)\;$» la dérivée temporelle de «$\;{\dfrac {\left[{\dot {\theta }}(t)\right]^{2}}{2}}\;$» et
• dans le 2^nd terme«$\;{\dfrac {m\;g\;{\mathfrak {a}}}{J_{\Delta _{O}}}}\;\sin \!\left[\theta (t)\right]\,{\dot {\theta }}(t)\;$»     celle de «$\;-{\dfrac {m\;g\;{\mathfrak {a}}}{J_{\Delta _{O}}}}\;\cos \!\left[\theta (t)\right]\;$»

     puis en intégrant entre «$\;t=0\;$» et «$\;t>0\;$» $\;{\big [}$les C.I. étant «$\;\theta (0)=\theta _{0}\;$ quelconque » et «$\;{\dot {\theta }}(0)={\dot {\theta }}_{0}\;$ également quelconque »${\big ]}\;$ «$\;{\dfrac {\left[{\dot {\theta }}(t)\right]^{2}}{2}}-{\dfrac {{\dot {\theta }}_{0}^{2}}{2}}-{\dfrac {m\;g\;{\mathfrak {a}}}{J_{\Delta _{O}}}}\;\cos \!\left[\theta (t)\right]+{\dfrac {m\;g\;{\mathfrak {a}}}{J_{\Delta _{O}}}}\;\cos(\theta _{0})=0\;$» soit finalement, en multipliant par «$\;J_{\Delta _{O}}\;$» et en basculant les termes constants dans le membre de droite l’équation différentielle du 1^er ordre en $\;\theta (t)\;$

«$\;{\dfrac {1}{2}}\;J_{\Delta _{O}}\,\left[{\dot {\theta }}(t)\right]^{2}-m\;g\;{\mathfrak {a}}\;\cos \!\left[\theta (t)\right]={\dfrac {1}{2}}\;J_{\Delta _{O}}\;{\dot {\theta }}_{0}^{2}-m\;g\;{\mathfrak {a}}\;\cos(\theta _{0})\quad \left({\mathfrak {1}}\right)\;$» ;

     nous verrons au paragraphe « énergie cinétique d'un système de points matériels indéformable en rotation autour d'un axe Δ fixe, de vecteur rotation instantanée connu » du chap.$9$ de la leçon « Mécanique 2 (PCSI) » que le 1^er terme «$\;{\dfrac {1}{2}}\;J_{\Delta _{O}}\,\left[{\dot {\theta }}(t)\right]^{2}\;$» du membre de gauche définit l’énergie cinétique du P.P.(N.A.) à l'instant $\;t\;$ et

     nous verrons au paragraphe « énergie potentielle de pesanteur du pendule pesant » du chap.$10$ de la leçon « Mécanique 2 (PCSI) » que le 2^nd terme «$\;-m\;g\;{\mathfrak {a}}\;\cos \!\left[\theta (t)\right]\;$» du membre de gauche définit l’énergie potentielle de pesanteur du P.P.(N.A.) avec « référence en position horizontale » au même instant $\;t\;$ et

     nous verrons au paragraphe « énergie mécanique du pendule pesant et sa conservation en absence de frottement » du chap.$10$ de la leçon « Mécanique 2 (PCSI) » que la somme des deux termes du membre de gauche «$\;{\dfrac {1}{2}}\;J_{\Delta _{O}}\,\left[{\dot {\theta }}(t)\right]^{2}-m\;g\;{\mathfrak {a}}\;\cos \!\left[\theta (t)\right]\;$» définit l'énergie mécanique du P.P.(N.A.) avec « référence en position horizontale », celle des deux termes du membres de droite définissant l'énergie mécanique initiale du P.P.(N.A.) avec « référence en même position horizontale », l'égalité des deux correspondant à la conservation de l'énergie mécanique du P.P.N.A. ;

     pour se ramener au choix usuel de la « référence de l’énergie potentielle de pesanteur en la position d’équilibre stable $\;\theta _{\text{éq. stable}}=0\;$», on ajoute de part et d’autre de l’équation $\;\left({\mathfrak {1}}\right)\;$ la quantité «$\;m\;g\;{\mathfrak {a}}\;$» pour reconnaître respectivement dans «$\;m\;g\;{\mathfrak {a}}\,\left\lbrace 1-\cos \!\left[\theta (t)\right]\right\rbrace \;$» et «$\;m\;g\;{\mathfrak {a}}\,\left[1-\cos \!\left(\theta _{0}\right)\right]\;$» l’énergie potentielle de pesanteur du P.P.(N.A.) à l’instant $\;t\;$ et à l’instant initial avec « référence en la position d’équilibre stable » d’où, en notant «$\;E_{m,\,0}={\dfrac {1}{2}}\;J_{\Delta _{O}}\;{\dot {\theta }}_{0}^{2}+m\;g\;{\mathfrak {a}}\,\left[1-\cos \!\left(\theta _{0}\right)\right]\;$» l'énergie mécanique initiale du P.P.(N.A.), la réécriture de l’intégrale 1^ère du mouvement du P.P.N.A. selon

«$\;E_{m}(t)={\dfrac {1}{2}}\;J_{\Delta _{O}}\,\left[{\dot {\theta }}(t)\right]^{2}+m\;g\;{\mathfrak {a}}\,\left\lbrace 1-\cos \!\left[\theta (t)\right]\right\rbrace =E_{m,\,0}\;$» dans laquelle
«$\;E_{m}(t)\;$ est l'énergie mécanique du P.P.(N.A.) à l'instant $\;t\;$» avec « référence en la position d’équilibre stable ».

Étude du mouvement du P.P.(N.A.) dans le cas général des élongations angulaires non petites par diagramme énergétique

     Étude analogue à celle exposée dans le paragraphe « étude d'un P.P.S. à un degré de liberté lancé dans des C.I. 1b par diagramme d'énergies potentielle et mécanique » du chap.$17$ de la leçon « Mécanique 1 (PCSI) » en remplaçant «$\;{\mathit {l}}\;$ par $\;{\mathfrak {a}}\;$», «$\;{\dfrac {1}{2}}\;m\;{\mathit {l}}^{\,2}\,\left[{\dot {\theta }}(t)\right]^{2}\;$ par $\;{\dfrac {1}{2}}\;J_{\Delta _{O}}\,\left[{\dot {\theta }}(t)\right]^{2}\;$» et «$\;{\dfrac {1}{2}}\;m\;{\mathit {l}}^{\,2}\;{\dot {\theta }}_{0}^{2}\;$ par $\;{\dfrac {1}{2}}\;J_{\Delta _{O}}\;{\dot {\theta }}_{0}^{2}\;$», les conclusions de la discussion étant rappelées ci-dessous :

• si «$\;E_{m,\,0}\;$ est $\;<\;$ à $\;2\;m\;g\;{\mathfrak {a}}\;$», le mouvement du P.P.N.A. est oscillatoire et périodique de période sous forme intégrale «$\;{\mathcal {T}}=4\;{\sqrt {\dfrac {J_{\Delta _{O}}}{m\;g\;{\mathfrak {a}}}}}\;\displaystyle \int _{0}^{\theta _{m}}{\dfrac {d\theta }{\sqrt {2\,\left[\cos(\theta )-\cos(\theta _{m})\right]}}}={\mathcal {T}}_{0}\;{\dfrac {2}{\pi }}\;\displaystyle \int _{0}^{\theta _{m}}{\dfrac {d\theta }{\sqrt {2\,\left[\cos(\theta )-\cos(\theta _{m})\right]}}}\;$» avec
  «$\;{\mathcal {T}}_{0}=2\;\pi \;{\sqrt {\dfrac {J_{\Delta _{O}}}{m\;g\;{\mathfrak {a}}}}}\;$» la période des petites élongations angulaires du P.P.N.A. et,
  «$\;\theta _{m}\;$» l'amplitude des oscillations déterminée par «$\;\theta _{m}=\arccos \!\left[1-{\dfrac {E_{m,\,0}}{m\;g\;{\mathfrak {a}}}}\right]=\arccos \!\left[\cos(\theta _{0})-{\dfrac {J_{\Delta _{O}}}{2\;m\;g\;{\mathfrak {a}}}}\;{\dot {\theta }}_{0}^{2}\right]\;$» ;
• si «$\;E_{m,\,0}\;$ est $\;>\;$ à $\;2\;m\;g\;{\mathfrak {a}}\;$» $\;{\big (}$nous supposons $\;\theta _{0}>0{\big )}$, le mouvement du P.P.N.A. est révolutif et périodique de période sous forme intégrale $\;\succ \;$si $\;{\dot {\theta }}_{0}\;$ est $\;>0$, «$\;{\mathcal {T}}={\dfrac {1}{2}}\;{\sqrt {\dfrac {J_{\Delta _{O}}}{m\;g\;{\mathfrak {a}}}}}\;\displaystyle \int _{\theta _{0}}^{\theta _{0}+2\,\pi }{\dfrac {d\theta }{\sqrt {{\dfrac {E_{m,\,0}}{2\;m\;g\;{\mathfrak {a}}}}-\sin ^{2}\!\left({\dfrac {\theta }{2}}\right)}}}\;$» ou «$\;{\mathcal {T}}={\dfrac {{\mathcal {T}}_{0}}{2\;\pi }}\;\displaystyle \int _{\theta _{0}}^{\theta _{0}+\pi }{\dfrac {d\theta }{\sqrt {{\dfrac {E_{m,\,0}}{2\;m\;g\;{\mathfrak {a}}}}-\sin ^{2}\!\left({\dfrac {\theta }{2}}\right)}}}\;$» avec
  «$\;{\mathcal {T}}_{0}=2\;\pi \;{\sqrt {\dfrac {J_{\Delta _{O}}}{m\;g\;{\mathfrak {a}}}}}\;$» la période des petites élongations angulaires du P.P.N.A. ou enfin,
  «$\;{\mathcal {T}}={\dfrac {{\mathcal {T}}_{0}}{2\;\pi }}\;\displaystyle \int _{0}^{\pi }{\dfrac {d\theta }{\sqrt {{\dfrac {E_{m,\,0}}{2\;m\;g\;{\mathfrak {a}}}}-\sin ^{2}\!\left({\dfrac {\theta }{2}}\right)}}}\;$» ou encore,
  $\;\succ \;$si $\;{\dot {\theta }}_{0}\;$ est $\;<0$, «$\;{\mathcal {T}}={\dfrac {1}{2}}\;{\sqrt {\dfrac {J_{\Delta _{O}}}{m\;g\;{\mathfrak {a}}}}}\;\displaystyle \int _{\theta _{0}}^{\theta _{0}-2\,\pi }{\dfrac {-d\theta }{\sqrt {{\dfrac {E_{m,\,0}}{2\;m\;g\;{\mathfrak {a}}}}-\sin ^{2}\!\left({\dfrac {\theta }{2}}\right)}}}\;$» ou «$\;{\mathcal {T}}={\dfrac {{\mathcal {T}}_{0}}{2\;\pi }}\;\displaystyle \int _{\theta _{0}}^{\theta _{0}-\pi }{\dfrac {-d\theta }{\sqrt {{\dfrac {E_{m,\,0}}{2\;m\;g\;{\mathfrak {a}}}}-\sin ^{2}\!\left({\dfrac {\theta }{2}}\right)}}}\;$» avec
  «$\;{\mathcal {T}}_{0}=2\;\pi \;{\sqrt {\dfrac {J_{\Delta _{O}}}{m\;g\;{\mathfrak {a}}}}}\;$» la période des petites élongations angulaires du P.P.N.A. ou enfin,
  «$\;{\mathcal {T}}={\dfrac {{\mathcal {T}}_{0}}{2\;\pi }}\;\displaystyle \int _{0}^{-\pi }{\dfrac {-d\theta }{\sqrt {{\dfrac {E_{m,\,0}}{2\;m\;g\;{\mathfrak {a}}}}-\sin ^{2}\!\left({\dfrac {\theta }{2}}\right)}}}\;$» $\;{\Bigg \{}$ou «$\;{\mathcal {T}}={\dfrac {{\mathcal {T}}_{0}}{2\;\pi }}\;\displaystyle \int _{\pi }^{0}{\dfrac {-d\theta }{\sqrt {{\dfrac {E_{m,\,0}}{2\;m\;g\;{\mathfrak {a}}}}-\sin ^{2}\!\left({\dfrac {\theta }{2}}\right)}}}\;$»${\Bigg \}}$,      ces dernières expressions de période dans le cas $\;{\dot {\theta }}_{0}>0\;$ ou $\;<0\;$ établissant la « dépendance de la période relativement à l'énergie mécanique initiale » ;
• si «$\;E_{m,\,0}\;$ est $\;=\;$ à $\;2\;m\;g\;{\mathfrak {a}}\;$» $\;{\big (}$nous supposons $\;\theta _{0}\in \left]-\pi \,,\,+\pi \right[{\big )}$, il y a mouvement du P.P.N.A. jusqu'à l'une des positions d'équilibres instables «$\;\theta _{\text{éq. inst.}}=\pm \pi \;$» où le P.P.N.A. s'arrête définitivement en absence de perturbations extérieures.

Différents portraits de phase du pendule pesant (non amorti à un degré de liberté), « bifurcation » entre mouvement « pendulaire » et révolutif

Équation des portraits de phase d’un P.P.(N.A.) dans le cas général d’« oscillations ou de mouvement révolutif »

     L’équation du portrait de phase d'un P.P.N.A. sous forme implicite étant l'intégrale 1^ère du mouvement de ce dernier «$\;{\dfrac {1}{2}}\;J_{\Delta _{O}}\,\left[{\dot {\theta }}(t)\right]^{2}+m\;g\;{\mathfrak {a}}\,\left\lbrace 1-\cos \!\left[\theta (t)\right]\right\rbrace =E_{m,\,0}\;$» déterminée au paragraphe « détermination de l'intégrale 1^ère du mouvement du P.P.(N.A.) à partir de l'équation différentielle du mouvement en θ(t) suivi par ce derneir » plus haut dans ce chapitre dans laquelle la constante «$\;E_{m,\,0}\;$» est égale à «$\;{\dfrac {1}{2}}\;J_{\Delta _{O}}\,{\dot {\theta }}_{0}^{2}+m\;g\;{\mathfrak {a}}\,\left[1-\cos(\theta _{0})\right]\;$» $\;{\big (}$avec $\;\theta _{0}\;$ ainsi que $\;{\dot {\theta }}_{0}\;$ quelconques${\big )}\;$ et l'intégrale 1^ère du mouvement du P.P.N.A. étant identique à celle d'un P.P.S.N.A. après substitution de «$\;{\mathit {l}}\;$ par $\;{\mathfrak {a}}\;$» et de «$\;m\;{\mathit {l}}^{\,2}\;$ par $\;J_{\Delta _{O}}\;$», nous pouvons refaire, aux substitutions près, l’étude exposée au paragraphe « propriétés des portraits de phase dans le cas général d'oscillations ou de mouvement révolutif d'un P.P.S. lancé dans les C.I. “1b U 1a” » du chap.$12$ de la leçon « Mécanique 1 (PCSI) » $\;\ldots$

Tracé des portraits de phase d’un P.P.(N.A.) dans le cas général d’« oscillations ou de mouvement révolutif »

     Revoir le paragraphe « tracé des portraits de phase dans le cas général d'oscillations ou de mouvement révolutif d'un P.P.S. lancé dans les C.I. “1b U 1a” » du chap.$12$ de la leçon « Mécanique 1 (PCSI) » $\;\ldots$

« Bifurcation » entre mouvement « pendulaire » et révolutif

     Nous observons deux types de mouvement « pendulaire ou révolutif » suivant la valeur du paramètre «$\;E_{m,\,0}\;$» ${\big (}$énergie mécanique initiale${\big )}\;$ et une allure du portrait de phase nettement différente suivant le type considéré :

• pour un mouvement pendulaire, le portrait de phase est fermé, décrit dans le « sens horaire », avec le point «$\;{\big (}\theta =0\,,\,{\dot {\theta }}=0{\big )}\;$» comme « centre de symétrie » lequel correspond à la position d’équilibre stable du P.P.(N.A.) ;
• pour un mouvement révolutif, le portrait de phase est ouvert, constitué de la répétition du motif de l'intervalle $\;\left]-\pi \,,\,\pi \right]$, répété
     $\;\succ \;$ « vers les $\;\theta \nearrow \;$ en restant dans le domaine des $\;{\dot {\theta }}>0\;$ si $\;{\dot {\theta }}_{0}>0\;$» ou
     $\;\succ \;$ « vers les $\;\theta \searrow \;$ en restant dans le domaine des $\;{\dot {\theta }}<0\;$ si $\;{\dot {\theta }}_{0}<0\;$»,
  le portrait de phase avec C.I. «$\;\left(\theta _{0}\,,\,{\dot {\theta }}_{0}<0\right)\;$» étant l’antisymétrique de celui avec C.I. «$\;\left(\theta _{0}\,,\,-{\dot {\theta }}_{0}>0\right)\;$»,
  les maxima de valeur absolue de vitesse angulaire «$\;\vert {\dot {\theta }}\vert \;$» étant obtenus pour les positions d’équilibre stable «$\;\theta _{\text{éq. st.}}=p\;2\,\pi ,\;\;p\in \mathbb {Z} \;$» et
  les minima              de valeur absolue de vitesse angulaire étant obtenus pour les positions d’équilibre instable «$\;\theta _{\text{éq. inst.}}=\left(2\;p+1\right)\,\pi ,\;\;p\in \mathbb {Z} \;$».

     Conclusion : La « bifurcation » entre les deux types de mouvement « pendulaire et révolutif » correspond à un portrait de phase particulier où le point générique s’arrête en la position d’équilibre instable accessible «$\;\theta _{\text{éq. inst.}}=+\pi \;$ pour $\;{\dot {\theta }}_{0}>0\;$» ou «$\;\theta _{\text{éq. inst.}}=-\pi \;$ pour $\;{\dot {\theta }}_{0}<0\;$», cet arrêt pouvant n’être que temporaire si une perturbation extérieure intervient $\;{\big [}$le point générique repartant dans le domaine des «$\;{\dot {\theta }}>0\;$» jusqu'à l’arrêt suivant correspondant au « précédent augmenté de $\;2\,\pi \;$» ou dans le domaine des «$\;{\dot {\theta }}<0\;$» jusqu'à l’arrêt suivant correspondant au « précédent diminué de $\;2\,\pi \;$», ceci suivant que le signe de la vitesse angulaire infiniment petite fournie par la perturbation $\;\ldots {\big ]}$.

Approche numérique : présentation du tracé des lois horaires du mouvement du pendule pesant (non amorti à un degré de liberté) suivant les conditions de lancement, non isochronisme des oscillations, formule de de Borda

     Le traitement effectué dans ce paragraphe est analogue à celui présenté dans le paragraphe « complément, résolution numérique de l'équation différentielle d'un P.P.S. dans les C.I. “1a” puis “1b”, tracé des diagrammes horaires de position et de vitesse ainsi que celui des portraits de phase correspondant » du chap.$12$ de la leçon « Mécanique 1 (PCSI) ».

Approche numérique : présentation du tracé des diagrammes horaires de position et de vitesse du mouvement du P.P.(N.A.) suivant les conditions de lancement

     Voir le paragraphe « résolution numérique de l'équation différentielle d'un P.P.S. dans les C.I. “1a” avec tracé des diagrammes horaires de position, de vitesse et du portrait de phase correspondant » du chap.$12$ de la leçon « Mécanique 1 (PCSI) » en remplaçant P.P.S.(N.A.) par P.P.(N.A.), les valeurs initiales d’abscisse angulaire et de vitesse angulaire proposées étant maintenues ainsi que la valeur de l’intensité de la pesanteur, la donnée de la longueur «$\;{\mathit {l}}=1,000\;m\;$» du P.P.S.(N.A.) devant être remplacée par celle du rapport «$\;{\dfrac {J_{\Delta _{O}}}{m\;{\mathfrak {a}}}}=1,000\;m\;$» $\;{\Big [}$on y trouve les lignes du programme « Scilab » utilisé pour tracer les diagrammes horaire de position et de vitesse dans les C.I. $\;\left(\theta _{0}=-120\,{\text{°}}\;,\;{\dot {\theta }}_{0}=0\right)\;$ ainsi que le tracé du portrait de phase correspondant${\Big ]}\;$ puis

     Voir le paragraphe « résolution numérique de l'équation différentielle d'un P.P.S. dans les C.I. “1b” telles que le pendule s'arrête à la position d'équilibre instable avec tracé des diagrammes horaires de position, de vitesse et du portrait de phase correspondant » du chap.$12$ de la leçon « Mécanique 1 (PCSI) » en remplaçant P.P.S.(N.A.) par P.P.(N.A.), les valeurs initiales d’abscisse angulaire et de vitesse angulaire proposées étant maintenues ainsi que la valeur de l’intensité de la pesanteur, la donnée de la longueur «$\;{\mathit {l}}=1,000\;m\;$» du P.P.S.(N.A.) devant être remplacée par celle du rapport «$\;{\dfrac {J_{\Delta _{O}}}{m\;{\mathfrak {a}}}}=1,000\;m\;$» $\;{\Big [}$on y trouve les lignes du programme « Scilab » utilisé pour tracer les diagrammes horaire de position et de vitesse dans les C.I. $\;\left\lbrace \theta _{0}=-120\,{\text{°}}\;,\;{\dot {\theta }}_{0}={\sqrt {2\;{\dfrac {g}{l}}\,\left[1+\cos(\theta _{0})\right]}}\simeq 3,13\,rad\cdot s^{-1}\right\rbrace \;$ ainsi que le tracé du portrait de phase correspondant${\Big ]}\;$ ensuite

     Voir le paragraphe « résolution numérique de l'équation différentielle d'un P.P.S. dans les C.I. “1b” telles que le pendule s'acquiert un mouvement révolutif avec tracé des diagrammes horaires de position, de vitesse et du portrait de phase correspondant » du chap.$12$ de la leçon « Mécanique 1 (PCSI) » en remplaçant P.P.S.(N.A.) par P.P.(N.A.), les valeurs initiales d’abscisse angulaire et de vitesse angulaire proposées étant maintenues ainsi que la valeur de l’intensité de la pesanteur, la donnée de la longueur «$\;{\mathit {l}}=1,000\;m\;$» du P.P.S.(N.A.) devant être remplacée par celle du rapport «$\;{\dfrac {J_{\Delta _{O}}}{m\;{\mathfrak {a}}}}=1,000\;m\;$» $\;{\Big [}$on y trouve les lignes du programme « Scilab » utilisé dans les C.I. $\;\left\lbrace \theta _{0}=-120\,{\text{°}}\;,\;{\dot {\theta }}_{0}=3,5\,rad\cdot s^{-1}>{\sqrt {2\;{\dfrac {g}{l}}\,\left[1+\cos(\theta _{0})\right]}}\simeq 3,13\,rad\cdot s^{-1}\right\rbrace \;$ permettant de tracer les diagrammes horaire de position et de vitesse ainsi que le portrait de phase correspondant${\Big ]}\;$ et enfin

     Voir le paragraphe « superposition des trois portraits de phase précédemment tracés » du chap.$12$ de la leçon « Mécanique 1 (PCSI) » en remplaçant P.P.S.(N.A.) par P.P.(N.A.), les valeurs initiales d’abscisse angulaire et de vitesse angulaire proposées étant maintenues ainsi que la valeur de l’intensité de la pesanteur, la donnée de la longueur «$\;{\mathit {l}}=1,000\;m\;$» du P.P.S.(N.A.) devant être remplacée par celle du rapport «$\;{\dfrac {J_{\Delta _{O}}}{m\;{\mathfrak {a}}}}=1,000\;m\;$».

Non isochronisme des oscillations

     Voir le paragraphe « étude du mouvement du P.P.(N.A.) dans le cas général des élongations angulaires non petites par diagramme énergétique » plus haut dans le chapitre ou

     Voir le paragraphe « absence d'isochronisme des oscillations d'un P.P.S.N.A. » du chap.$17$ de la leçon « Mécanique 1 (PCSI) » dans lequel on remplace « P.P.S.(N.A.) » par « P.P.(N.A.) », «$\;{\mathit {l}}\;$ par $\;{\mathfrak {a}}\;$», «$\;m\;{\mathit {l}}^{\,2}\;$ par $\;J_{\Delta _{O}}\;$» et on adapte les C.I. pour généraliser le résultat obtenu, celles-ci étant $\;\left(\theta _{0}\;,\;{\dot {\theta }}_{0}\neq 0\right)\;$ satisfaisant un mouvement pendulaire d'amplitude $\;\theta _{m}$ $\;{\bigg \{}$c'est-à-dire telles que «$\;E_{m,\,0}=$ ${\dfrac {1}{2}}\;J_{\Delta _{O}}\;{\dot {\theta }}_{0}^{2}+m\;g\;{\mathfrak {a}}\,\left[1-\cos \!\left(\theta _{0}\right)\right]\;$ est $\;<\;$ à $\;2\;m\;g\;{\mathfrak {a}}\;$», l'amplitude des oscillations étant déterminée par «$\;\theta _{m}=\arccos \!\left[1-{\dfrac {E_{m,\,0}}{m\;g\;{\mathfrak {a}}}}\right]=\arccos \!\left[\cos(\theta _{0})-{\dfrac {J_{\Delta _{O}}}{2\;m\;g\;{\mathfrak {a}}}}\;{\dot {\theta }}_{0}^{2}\right]\;$»${\bigg \}}$, «$\;\vert \theta _{0}\vert \;$ devant être substitué par $\;\theta _{m}\;$ dans le résultat de la période sous forme intégrée » du paragraphe précité d'où l'expression de la période d'un P.P.N.A. sous forme intégrale dans laquelle «$\;{\mathcal {T}}_{0}=2\;\pi \;{\sqrt {\dfrac {J_{\Delta _{O}}}{m\;g\;{\mathfrak {a}}}}}\;$» est la période des petites élongations angulaires du P.P.N.A. suivi de sa réécriture $\;{\big (}$sans nouvelle démonstration${\big )}\;$ prouvant le non isochronisme de ce dernier :

«$\;{\mathcal {T}}={\mathcal {T}}_{0}\;{\dfrac {2}{\pi }}\;\displaystyle \int _{0}^{\theta _{m}}{\dfrac {d\theta }{\sqrt {2\,\left[\cos(\theta )-\cos(\theta _{m})\right]}}}\;{\overset {\cdots }{\;=\;}}\;{\mathcal {T}}_{0}\;{\dfrac {2}{\pi }}\;\displaystyle \int _{u=0}^{u={\frac {\pi }{2}}}{\dfrac {du}{\sqrt {1-\sin ^{2}\!\!\left({\dfrac {\theta _{m}}{2}}\right)\,\sin ^{2}(u)}}}\;$».

Formule de de Borda

La formule de de Borda n'étant pas au programme de physique de P.C.S.I. est donnée à titre documentaire.

     Voir le paragraphe « complément, évaluation numérique de la période et comparaison avec l'“expression approchée de de Borda” d'un P.P.S.N.A. en mouvement oscillatoire » du chap.$17$ de la leçon « Mécanique 1 (PCSI) » en l’adaptant au cas d’un P.P.N.A. en mouvement pendulaire, ce qui donne l’« expression approchée de de Borda de la période d’oscillations »

«$\;{\mathcal {T}}\simeq {\mathcal {T}}_{0}\left(1+{\dfrac {\theta _{m}^{2}}{16}}\right)\;$ dans laquelle $\;\theta _{m}\;$ est l'amplitude des oscillations exprimée en $\;rad\;$ et
«$\;{\mathcal {T}}_{0}=2\;\pi \;{\sqrt {\dfrac {J_{\Delta _{O}}}{m\;g\;{\mathfrak {a}}}}}\;$» la période des « petites élongations angulaires ».

     Remarques : L'évaluation de la « période par formule de de Borda » donne un résultat en accord avec celui obtenu en évaluant « l'intégrale selon laquelle la période est explicitée » et ceci, pour des valeurs de $\;\theta _{m}\;$ non petites $\;{\bigg [}$celles-ci devant être $\;\lesssim \;$ à $\;{\dfrac {5\;\pi }{12}}\;rad=75\,{\text{°}}\;$ pour donner un résultat correct à $\;1\,\%\;$ près${\bigg ]}$.

     Remarques : Pour l'évaluation de la « période explicitée sous forme intégrale » voir le paragraphe « complément, évaluation numérique de la période et comparaison avec l'“expression approchée de de Borda” d'un P.P.S.N.A. en mouvement oscillatoire » du chap.$17$ de la leçon « Mécanique 1 (PCSI) » en l’adaptant au cas d’un P.P.N.A. en mouvement pendulaire $\;{\big (}$la C.I. de vitesse angulaire du P.P.S.N.A. dans l'évaluation de sa période sous forme intégrale étant $\;{\dot {\theta }}_{0}=0$, l'amplitude des oscillations est égale à $\;\vert \theta _{0}\vert {\big )}$, la comparaison avec la « période par formule de de Borda » donnant :

• pour $\;\theta _{m}={\dfrac {\pi }{3}}\;rad=60\,{\text{°}}\;$ on trouve un écart relatif de $\;0,43\;\%\;$ entre la « période sous forme intégrale » et « l'expression approchée de de Borda », cette dernière sous-estimant la période ;
• pour $\;\theta _{m}={\dfrac {2\;\pi }{3}}\;rad=120\,{\text{°}}\;$ on trouve un écart relatif de $\;7,19\;\%\;$ entre la « période sous forme intégrale » et « l'expression approchée de de Borda », cette dernière sous-estimant la période ;
• pour $\;\theta _{m}={\dfrac {5\;\pi }{6}}\;rad=150\,{\text{°}}\;$ on trouve un écart relatif de $\;18,94\;\%\;$ entre la « période sous forme intégrale » et « l'expression approchée de de Borda », cette dernière sous-estimant la période.

Réalisation expérimentale du portrait de phase d’un pendule pesant (non amorti à un degré de liberté), mise en évidence d’un amortissement (correspondant à une diminution d’« énergie mécanique »)

Description du dispositif expérimental

Dispositif expérimental de détermination du diagramme horaire de position angulaire d'un pendule pesant dont l'axe de rotation est solidaire d'un potentiomètre 10 tours

     Bien que nous souhaitons étudier un P.P.N.A., les frottements fluide $\;{\big (}$et solide${\big )}\;$ ne peuvent jamais être totalement éliminés, ils ne peuvent qu'être réduits, la réduction sera considérée comme satisfaisante pour un mouvement pendulaire si les oscillations se maintiennent pendant une « durée suffisamment grande devant la période » ;

     nous pouvons utiliser le pendule pesant, schématisé ci-contre, composé des pièces suivantes :

• une tige cylindrique, de C.D.I. $\;G_{t}$, de masse $\;m_{t}$, de longueur $\;{\mathit {l}}_{t}\;$ et de rayon $\;R_{t}$, pouvant être fixée en $\;O\;$ sur un axe horizontal de rotation $\;{\big (}$l’axe du potentiomètre décrit ci-après${\big )}$,
• un cylindre métallique, de C.D.I. $\;G_{c}$, de masse $\;m_{c}$, de longueur $\;{\mathit {l}}_{c}$, de rayon extérieur $\;R_{2}\;$ et de rayon intérieur $\;R_{1}$, dont l'axe est confondu avec l'axe de la tige et que nous pouvons déplacer sur cette dernière pour modifier la position du C.D.I. global et du moment d’inertie du pendule relativement à l’axe de rotation,
• un potentiomètre bobiné $\;10\;$ tours de $\;10\;k\Omega$ $\;{\big (}$voir ci-dessous à droite${\big )}$, d’axe servant d’axe de rotation au pendule ;
     le potentiomètre est alimenté symétriquement à l'aide d'une A.S. entre $\;+12\;V\;$ et $\;-12\;V$, la position angulaire du pendule étant alors $\;\propto \;$ à la tension «$\;u(t)\;$» entre le curseur du potentiomètre et la masse de l’alimentation ;
     lorsque le pendule est au repos, le curseur est placé approximativement à mi-course et le support du potentiomètre est tourné de manière à obtenir une tension «$\;u_{\text{éq}}\;$» à l’équilibre inférieure à $\;10\;mV\;$, l’échelle de tension est alors de «$\;300\;mV\;$ pour $\;45\;{\text{°}}\;$» $\;{\Big \{}$en effet $\;24\;V\;$ aux bornes des $\;10\;$ tours de potentiomètre donne $\;2,4\;V\;$ par tour et $\;0,3\;V\;$ pour $\;{\dfrac {1}{8}}\;$ de tour correspondant à une élongation angulaire de $\;{\dfrac {\pi }{4}}\;rad=45\;{\text{°}}{\Big \}}$ ;

Centrale de conversion Eurosmart SysamSP5 pilotée par interface python

Exemple de potentiomètre $\;10\;$ tours de $\;10\;k\Omega$

     l'acquisition de la tension peut être faite avec la « centrale de conversion Eurosmart SysamSP5 » $\;{\big (}$ci-contre à gauche${\big )}\;$ pilotée par interface « python », voir le paragraphe « utilisation de la centrale de conversion Eurosmart SysamSP5 pilotée par l'interface python » suivant.

     Remarque : on pourrait utiliser une autre interface mais le potentiomètre devrait être adapté, par exemple avec l’interface « Orphy-GTI » avec sa prise $\;F$, utiliser un potentiomètre monotour de $\;10\;k\Omega \;$ en mettant en série avec lui deux autres conducteurs ohmiques additionnels de même résistance de $\;10\;k\Omega$, « la tension appliquée au potentiomètre étant alors de $\;8\;V\;$», l’échelle de tension est de «$\;1\;V\;$ pour $\;45\;{\text{°}}\;$», l’interface « Orphy-GTI » étant reliée à l’ordinateur par la prise « série $\;COM2\;$», voir le paragraphe « utilisation de l'interface “ORPHY-GTI” associée au logiciel “Regressi” » plus loin dans le chapitre
     Remarque : $\;{\big [}$voir un exemple de potentiomètre monotour $\;10\;k\Omega \;$ et l'interface “ORPHY-GTI” associée au logiciel “Regressi” respectivement à droite et à gauche dans le paragraphe en question « utilisation de l'interface “ORPHY-GTI” associée au logiciel “Regressi” » plus loin dans le chapitre${\big ]}$.

Utilisation de la centrale de conversion Eurosmart SysamSP5 pilotée par l’interface python

     On réalise une acquisition de la tension $\;u(t)\;$ avec une période d’échantillonnage de $\;10\;ms\;$ et pendant une durée de $\;70\;s\;$ $\;{\big (}$correspondant donc à $\;7000\;$ valeurs captées $\Rightarrow$ la durée d’acquisition est suffisamment grande pour observer un retour à l’équilibre du pendule${\big )}\;$, le code python permettant de faire l'acquisition est le suivant :

import pycanum.main as pycan
import matplotlib.pyplot as plt

import numpy
import math

sys = pycan.Sysam("SP5")
sys.config_entrees([0],[1])
te=1e-2 # période d'échantillonnage
ne=7000 # nombre d'échantillons
duree=te*ne
sys.config_echantillon(te*10**6,ne)           # période d'échantillonnage en µs
sys.acquerir()
t=sys.temps()
u=sys.entrees()
echelle = 0.6/(math.pi/2)           # conversion tension->angle
angle=u[0]/echelle
temps=t[0]
numpy.savetxt("pendule-6.txt",[temps,angle])
sys.fermer()
plt.figure(figsize=(18,6))           # taille en pouces 18,6 inch = 47,2 cm

plt.plot(temps,angle)
plt.xlabel("t (s)")
plt.ylabel("theta (rad)")
plt.axis([0,duree,-math.pi/2,math.pi/2])
plt.show()

Diagramme horaire de position angulaire d'un P.P.A. écarté de sa position d'équilibre stable et lâché sans vitesse initiale, obtenu par centrale de conversion Eurosmart SysamSP5 pilotée par l’interface python

Diagramme horaire de vitesse angulaire d'un P.P.A. écarté de sa position d'équilibre stable et lâché sans vitesse initiale, obtenu par filtre dérivateur du signal échantillonné bruité acquis par centrale de conversion Eurosmart SysamSP5 pilotée par l’interface python

     puis on trace le diagramme horaire de l’élongation angulaire, le code python pour obtenir le tracé ci-contre est ci-dessous

from matplotlib.pyplot import *           # importe tous les noms du module sauf ceux commençant par "_"
import numpy as np
import math
import scipy.signal

[temps,angle] = np.loadtxt("pendule-6.txt")
figure(figsize=(10,6))           # taille en pouces 10,6 inch = 26,9 cm
plot(temps,angle)
xlabel("t (s)")
ylabel("theta (rad")
axis([0,70,-2,2])
grid()           # ajoute une grille de fond sur la figure

     ensuite l'objectif est d'en déduire le diagramme horaire de vitesse angulaire du P.P.A. par dérivation du signal échantillonné, ce qui se fait par simulation de filtre dérivateur «$\;x\mapsto y\;{\text{:}}\;y_{n}={\dfrac {x_{n}-x_{n-1}}{T_{e}}}\;$» avec «$\;T_{e}\;$ la période d’échantillonnage » mais le signal obtenu étant « très bruité » il faudrait effectuer une simulation de filtre passe-bas avant de dériver, le code python pour dériver puis tracer le diagramme horaire de vitesse angulaire sans élimination préalable du bruit est ci-dessous avec le tracé ci-contre

a=[te]           # dénominateur du quotient définissant le filtre dérivateur
b=[1,-1]           # le 1^er et 2^nd cœfficients de la somme du numérateur du quotient définissant le filtre dérivateur
omega = scipy.signal.lfilter(b,a,angle)
figure(figsize=(10,6))           # taille en pouces 10,6 inch = 26,9 cm
plot(temps,omega)
xlabel("t (s)")
ylabel("omega (rad/s")
axis([0,70,-10,10])
grid()           # ajoute une grille de fond sur la figure

     on y voit nettement la nécessité de filtrer le signal échantillonné avant de dériver, ce qu'on va exposer ci-dessous :

     on réalise donc une simulation de filtre passe-bas en utilisant un « filtre à R.I.F. » qui est basée sur une réponse C.L. d’un nombre fini de valeurs du signal d’entrée selon «$\;y_{n}=\!\!\sum \limits _{k\,\in \,\left[\left[-P\,,\,P\right]\right]}b_{k}\;x_{n-k}\;$», les $\;2\;P+1\;$ cœfficients «$\;b_{k}\;$» étant des constantes réelles « définissant le filtrage », le code python pour réaliser ce filtrage passe-bas étant ci-dessous avec le tracé ci-contre du diagramme horaire de position filtrée en rouge superposé à celui du diagramme horaire de position bruitée en bleu sur l'intervalle $\;\left[50\;s\;;\;60\;s\right]$ :

Superposition des diagrammes horaires de position angulaire bruitée (en bleu) et filtrée (en rouge) d'un P.P.A. écarté de sa position d'équilibre stable et lâché sans vitesse initiale, obtenu par centrale de conversion Eurosmart SysamSP5 pilotée par l’interface python, les tracés étant localisés vers la fin des oscillations

P=20           # un rang de troncature de P = 20 petit devant ne = 7000 mais suffisamment grand pour que le filtre soit sélectif
fc=0.05           # une fréquence de coupure de 0,05 Hz suffisamment petite pour éliminer le maximum de bruit sans altérer le signal

h = scipy.signal.firwin(numtaps=2*P+1,cutoff=[fc],nyq=0.5,window='hamming')           # utilise le module « filtre à R.I.F. »
y = scipy.signal.convolve(angle,h,mode='valid')           # réalise le filtrage par convolution du signal θ par le filtre passe-bas simulé

ny = y.size           # définit le nombre de points de la liste « y » du signal filtré
ty = np.zeros(ny)           # définit une liste « ty » contenant ny zéros
for k in range(ny):                    # remplace chaque zéro de la liste « ty » par l'instant …
     ty[k] = P*te+te*k           # … correspondant à la valeur de même rang dans la liste « y »

figure(figsize=(10,6))           # taille en pouces 10,6 inch = 26,9 cm
plot(temps,angle,"b")           # tracé du diagramme horaire de position bruitée en bleu
plot(ty,y,"r")           # tracé du diagramme horaire de position filtrée en rouge
xlabel("t (s)")
ylabel("theta (rad)")
axis([50,60,-0.3,0.3])
grid()           # ajoute une grille de fond sur la figure

Diagramme horaire de vitesse angulaire d'un P.P.A. écarté de sa position d'équilibre stable et lâché sans vitesse initiale, obtenu par filtre dérivateur du signal échantillonné acquis par centrale de conversion Eurosmart SysamSP5 pilotée par l’interface python puis débarrassé du bruit par filtrage passe-bas

     ensuite on obtient le diagramme horaire de vitesse angulaire du P.P.A. par dérivation du signal échantillonné filtré, ce qui se fait par simulation de filtre dérivateur «$\;x\mapsto y\;{\text{:}}\;y_{n}={\dfrac {x_{n}-x_{n-1}}{T_{e}}}\;$» avec «$\;T_{e}\;$ la période d’échantillonnage », le code python pour dériver le signal échantillonné débarrassé du bruit puis tracer le diagramme horaire de vitesse angulaire correspondant est ci-dessous avec le tracé ci-contre

a=[te]           # dénominateur du quotient définissant le filtre dérivateur
b=[1,-1]           # le 1^er et 2^nd cœfficients de la somme du numérateur du quotient définissant le filtre dérivateur
omega = scipy.signal.lfilter(b,a,y)
figure(figsize=(10,6))           # taille en pouces 10,6 inch = 26,9 cm
plot(ty,omega)
xlabel("t (s)")
ylabel("omega (rad/s)")
axis([0,70,-10,10])
grid()           # ajoute une grille de fond sur la figure

Portrait de phase d'un P.P.A. écarté de sa position d'équilibre stable et lâché sans vitesse initiale, obtenu par centrale de conversion Eurosmart SysamSP5 pilotée par l’interface python, avec élimination du bruit sur l'élongation angulaire par filtrage passe-bas et obtention de la vitesse angulaire par filtrage dérivateur

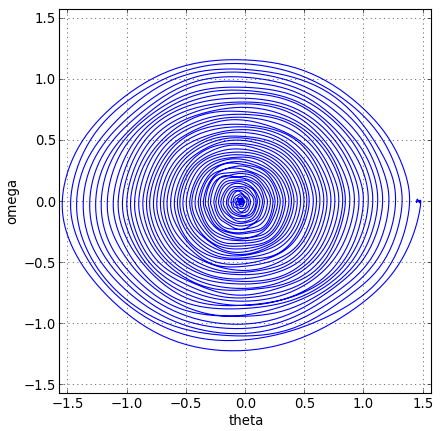
     enfin souhaitant tracer le portrait de phase du P.P.A. à partir de son point de lancement, on élimine les 1^ères valeurs des listes de temps «$\;ty\;$», de positions angulaires «$\;y\;$» et de vitesses angulaires «$\;{\text{omega}}\;$» susceptibles de correspondre à un enregistrement antérieur au lancement $\;{\big (}$celle de vitesses angulaires étant divisée par $\;2\;\pi \;$ de façon à ce que ces dernières soient exprimées en $\;{\text{tour}}\cdot s^{-1}{\big )}$, le code python pour ces transformations et le tracé du portrait de phase est ci-dessous avec le tracé ci-contre

debut = int(1.0/te)           # retourne un entier à partir de 1.0/te
y = np.delete(y,range(debut))           # supprime les éléments de la liste « y » de rang dans l'intervalle [ 0, int(1.0/te) [ des entiers naturels
ty = np.delete(ty,range(debut))           # supprime les éléments de la liste « ty » de rang dans l'intervalle [ 0, int(1.0/te) [ des entiers naturels
omega = np.delete(omega,range(debut))/(2*math.pi)           # supprime les éléments de la liste « omega » de rang dans …
                                                                                              # … l'intervalle [ 0, int(1.0/te) [ des entiers naturels puis divise par 2*π
figure(figsize=(6,6))           # taille en pouces 6,6 inch = 16,7 cm
plot(y,omega)
axis([-math.pi/2,math.pi/2,-math.pi/2,math.pi/2])
xlabel("theta")
ylabel("omega")
grid()           # ajoute une grille de fond sur la figure

     Remarque : On peut aisément imaginer les allures des différents diagrammes et portrait de phase d'un P.P.N.A. à partir de celles du P.P.A. obtenues ci-dessus, l'absence d'amortissement se manifestant par une amplitude de l'élongation angulaire et de la vitesse angulaire constante et par un portrait de phase fermé sur lui-même $\;\ldots$

Utilisation de l’interface « ORPHY-GTI » associée au logiciel « Regressi »

     Le programme de physique de P.C.S.I. impose d’obtenir le diagramme horaire d’élongation angulaire, la variation de la période avec l’amplitude et d’étudier les frottements solide puis fluide d'un pendule pesant « sans aborder le tracé du portrait de phase » en utilisant le logiciel « Regressi » ; ci-après est proposée

Exemple de potentiomètre monotour de $\;10\;k\Omega$

Interface ORPHY-GTI à associer au logiciel Regressi

Photo du dispositif « Pendulor » pour étudier le mouvement d'un P.P.A.

     une 1^ère manipulation avec utilisation de l’interface « ORPHY-GTI » $\;{\big (}$voir ci-contre à gauche${\big )}\;$ associée au logiciel « Regressi » $\;{\big [}$on peut utiliser le dispositif du paragraphe « description du dispositif expérimental (remarque) » présenté plus haut dans ce chapitre, le potentiomètre utilisé devant être monotour $\;{\big (}$comme celui représenté ci-contre à droite${\big )}\;$ et le pendule étant du type « Pendulor » comme sur la photo ci-dessous à gauche $\;{\big (}$dans lequel on remarque un cylindre de plastique situé au-delà de $\;\Delta _{O}\;$ permettant d'y fixer une plaque créant des frottements fluides${\big )}{\big ]}$,
     une 1^ère manipulation peut être visualisée à l'adresse « http://www.sciences.univ-nantes.fr/sites/jacques_charrier/tp/pendulor/index.html », nous n'en dirons rien de plus, les lecteurs intéressés pouvant aisément s'y référer $\;{\big \{}$il y est possible de visualiser les différentes étapes sans que le lancement d'une acquisition ne soit nécessaire mais en cliquant simplement sur les différents liens successifs$\}$ $\;\ldots$

Autre utilisation de la centrale de conversion Eurosmart SysamSP5 associée aux logiciels « Synchronie 2003 » et « Regressi »

     Dans ce paragraphe est proposée une 2^nde manipulation utilisant la centrale de conversion Eurosmart SysamSP5 $\;{\big [}$on peut utiliser le dispositif du paragraphe « description du dispositif expérimental » présenté plus haut dans ce chapitre, le potentiomètre utilisé devant être monotour $\;{\big (}$comme celui représenté ci-dessus à droite${\big )}\;$ et le pendule étant du type « Pendulor » comme sur la photo ci-contre à gauche $\;{\big (}$dans lequel on remarque un cylindre de plastique situé au-delà de $\;\Delta _{O}\;$ permettant d'y fixer une plaque créant des frottements fluides, les éventuels frottements solides se manifestant au niveau de l'axe de rotation$\;\Delta _{O}{\big )}{\big ]}$, la centrale Eurosmart SysamSP5 étant maintenant pilotée par « Synchronie 2003 » et les calculs ainsi que les tracés effectués par le logiciel « Regressi ».

     $\;\succ \;$Paramétrage du logiciel « Synchronie 2003 » et réglage du zéro : l'acquisition de la tension $\;u(t)\;$ sera faite avec une période d’échantillonnage de $\;2,5\;ms\;$ et pendant une durée de $\;2,5\;s$ $\;{\big (}$il y aura donc $\;1000\;$ valeurs captées${\big )}$ $\;{\big [}$pour les acquisitions de la tension avec prise en compte des frottements solide ou fluide, la durée d'enregistrement sera augmentée à $\;12\;s\;$ avec la même période d'échantillonnage, ce qui correspondra à $\;4800\;$ valeurs captées, ceci dans le but de visualiser l'amortissement${\big ]}$ ; le réglage du zéro est celui qui a été exposé dans le paragraphe « description du dispositif expérimental (on tourne le support du potentiomètre de façon à ce que la tension captée quand le pendule est à l'équilibre soit inférieure à 10 mV) » plus haut dans ce chapitre et on vérifie, en lançant une acquisition de tension lorsque que le pendule est maintenu avec une élongation de $\;{\dfrac {\pi }{2}}\;rad=90\,{\text{°}}$ $\;{\big (}$on trouve $\;V1\simeq 6,0\;V{\big )}\;$, l'échelle de correspondance «$\;3,00\;V\;$ pour $\;45\;{\text{°}}\;$» $\;{\Big \{}$en effet $\;24\;V\;$ pour un tour de potentiomètre donne $\;3\;V\;$ pour $\;{\dfrac {1}{8}}\;$ de tour correspondant à une élongation angulaire de $\;{\dfrac {\pi }{4}}\;rad=45\;{\text{°}}{\Big \}}$.

     $\;\succ \;$Enregistrements des oscillations et sauvegarde de ces derniers : on lance successivement $\;2\;$ acquisitions après avoir écarté le pendule pesant de sa position d'équilibre stable et l'avoir lâché sans vitesse initiale

• la 1^ère correspondant à une grande amplitude $\;{\big (}$voisine de $\;60\;{\text{°}}{\big )}\;$ avec frottements négligeables sur la durée de l'expérience $\;2,5\;s\;$ et
• la 2^nde correspondantà une grande amplitude $\;{\big (}$voisine de $\;60\;{\text{°}}{\big )}\;$ avec frottements solide et fluide non négligeables sur la durée de l'expérience $\;12\;s$, puis

            Enregistrements des oscillations et sauvegarde de ces derniers :on sauvegarde chaque enregistrement dans un fichier différent au format « .txt » en précisant les variables «$\;T\;$» et «$\;EAO\;$» $\;{\big (}$c'est-à-dire la tension associée à l'élongation angulaire${\big )}$.

     $\;\succ \;$Tracé des diagrammes horaires des positions angulaires à l'aide de « Regressi » : on peut alors ouvrir chaque fichier à l'aide de « Regressi », on obtient un tableau donnant «$\;T\;$» et «$\;EAO\;$», on modifie alors «$\;T\;$» en «$\;t\;$» et on crée la nouvelle variable «$\;\theta \;$» à partir de «$\;EAO\;$» selon «$\;\theta =EAO\times {\dfrac {90}{V1}}\;$» $\;{\big (}\theta \;$ étant l'élongation angulaire du pendule exprimée en $\;{\text{°}}{\big )}\;$ puis on enregistre chaque fichier modifié au format « .rw3 ».

Diagramme horaire de position angulaire d'un P.P.N.A. écarté de sa position d'équilibre stable et lâché sans vitesse initiale, l'acquisition ayant été faite par centrale de conversion Eurosmart SysamSP5 associée aux logiciels « Synchronie 2003 » et « Regressi »

Portrait de phase d'un P.P.N.A. écarté de sa position d'équilibre stable et lâché sans vitesse initiale, l'acquisition ayant été faite par centrale de conversion Eurosmart SysamSP5 associée aux logiciels « Synchronie 2003 » et « Regressi »

Diagramme horaire de position angulaire d'un P.P.A. écarté de sa position d'équilibre stable et lâché sans vitesse initiale, l'acquisition, sur une durée permettant d'observer le début des pseudo-oscillations, ayant été faite par centrale de conversion Eurosmart SysamSP5 associée aux logiciels « Synchronie 2003 » et « Regressi »

• Diagramme horaire de position angulaire du P.P.N.A. : ayant écarté le P.P.N.A. de $\;\theta _{0}\simeq +{\dfrac {\pi }{3}}\;rad\simeq 60\;{\text{°}}\;$ de sa position d'équilibre stable et l'ayant lâché sans vitesse initiale, nous lançons l'acquisition à l'aide de « Synchronie 2003 » sur une durée de $\;2,5\;s\;$ après avoir déterminé l'échelle de conversion des tensions en angles en mesurant $\;V1=6,06\;V\;$ $\Rightarrow$ «$\;\theta =EAO\times {\dfrac {90}{6,06}}\simeq 14,85\;EAO\;$» $\;{\big (}\theta \;$ étant en $\;{\text{°}}\;$ et $\;EAO\;$ en $\;V{\big )}$, enregistrons l'acquisition dans un fichier nommé « PPNA_t_theta.txt », l'ouvrons dans « Regressi », le transformons comme indiqué ci-dessus et sauvons le résultat dans un fichier nommé « PPNA_t_theta.rw3 », le diagramme horaire de position angulaire du P.P.N.A. obtenu par « Regressi » étant présenté ci-contre :
     on y détermine une période de «$\;{\mathcal {T}}\simeq 1,50\;s\;$» avec une amplitude «$\;\theta _{m}\simeq 69,2\;{\text{°}}\;$» et bien que le tracé semble, à 1^ère vue, sinusoïdal, on pourrait vérifier qu'il ne l'est pas tout en restant périodique.
• Diagramme horaire de vitesse angulaire du P.P.N.A. : ouvrant le fichier « PPNA_t_theta.rw3 » dans « Regressi » correspondant à l'acquisition des positions angulaires du P.P.N.A. écarté de $\;\theta _{0}\simeq +{\dfrac {\pi }{3}}\;rad\simeq 60\;{\text{°}}\;$ de sa position d'équilibre stable et lâché sans vitesse initiale, nous évaluons la vitesse angulaire par « Regressi » selon le mode opératoire décrit ci-après « dans le menu “Grandeurs” du fichier, sélectionner “Tableau”, cliquer sur “ajouter (une colonne)” puis sélectionner “dérivée” en renseignant tout ce qui est demandé, une fois la colonne de vitesse angulaire établie aller dans le menu “Graphe” du fichier, sélectionner le tracé de la vitesse angulaire en fonction du temps, on visualise alors le diagramme horaire de vitesse angulaire $\;{\big (}$sans que les différents points successifs ne soient reliés${\big )}$, terminer en faisant la sauvegarde du fichier sous le nom “PPNA_t_theta_omega.rw3” » $\;{\big [}$tracé non fourni, il est légèrement triangularisé avec une amplitude $\simeq 230\,{\text{°}}\cdot s^{-1}{\big ]}$.
• Portrait de phase du P.P.N.A. : à partir du fichier « PPNA_t_theta_omega.rw3 » ouvert dans « Regressi » correspondant à l'acquisition des positions angulaires du P.P.N.A. écarté de $\;\theta _{0}\simeq +{\dfrac {\pi }{3}}\;rad\simeq 60\;{\text{°}}\;$ de sa position d'équilibre stable et lâché sans vitesse initiale, à laquelle a été ajoutée l'évaluation de la vitesse angulaire correspondant aux différents instants de l'acquisition, on trace le portrait de phase du P.P.N.A. selon le mode opératoire suivant « dans le menu “Graphe” du fichier, sélectionner l'élongation angulaire comme abscisse et la vitesse angulaire comme ordonnée », on obtient alors le portrait de phase ci-contre ; même si le tracé obtenu semble, à 1^ère vue, une ellipse, on pourrait vérifier qu'il n'en est rien, le portrait de phase restant néanmoins fermé, ceci étant caractéristique d'un mouvement périodique $\;\ldots$

• Diagramme horaire de position angulaire du P.P.A. : ayant écarté le P.P.A. de $\;\theta _{0}\simeq 10\;{\text{°}}\simeq +{\dfrac {\pi }{18}}\;rad\;$ de sa position d'équilibre stable et l'ayant lâché sans vitesse initiale, nous lançons l'acquisition à l'aide de « Synchronie 2003 » sur une durée de $\;12\;s$, après avoir vérifié que l'échelle de conversion des tensions en angles reste inchangée en mesurant $\;V1=6,06\;V\;$ $\Rightarrow$ «$\;\theta =EAO\times {\dfrac {90}{6,06}}\simeq 14,85\;EAO\;$» $\;{\big (}\theta \;$ étant en $\;{\text{°}}\;$ et $\;EAO\;$ en $\;V{\big )}$, enregistrons l'acquisition dans un fichier nommé « PPA_t_theta.txt », l'ouvrons dans « Regressi », le transformons comme indiqué ci-dessus et sauvons le résultat dans un fichier nommé « PPA_t_theta.rw3 », le diagramme horaire de position angulaire du P.P.A. obtenu par « Regressi » étant présenté ci-contre :
     on y détermine une pseudo-période de «$\;{\mathcal {T}}\simeq 1,49\;s\;$» avec une amplitude de la 1^ère pseudo-oscillation «$\;\theta _{m,\,1}\simeq 10,1\;{\text{°}}\;$», la $\;\searrow \;$ de la pseudo-amplitude étant exponentielle on peut définir le décrément logarithmique $\;\delta =\ln \!\left[{\dfrac {\theta (t)}{\theta (t+{\mathcal {T}})}}\right]=$ ${\dfrac {1}{n}}\;\ln \!\left[{\dfrac {\theta (t)}{\theta (t+n\;{\mathcal {T}})}}\right]\;$ dont la valeur est «$\;\delta \simeq 0,112\;$» d'où l'évaluation de la constante de temps d'amortissement $\;\tau ={\dfrac {\mathcal {T}}{\delta }}\simeq$ $13,3\;s$ $\;{\bigg [}$la pseudo-amplitude $\;\searrow \;$ selon $\;\exp \!\left(-{\dfrac {t}{\tau }}\right)\;$ $\Rightarrow$ $\;\delta ={\dfrac {\mathcal {T}}{\tau }}{\bigg ]}$.
• Diagramme horaire de vitesse angulaire du P.P.A. : ouvrant le fichier « PPA_t_theta.rw3 » dans « Regressi » correspondant à l'acquisition des positions angulaires du P.P.A. écarté de $\;\theta _{0}\simeq 10\;{\text{°}}\simeq +{\dfrac {\pi }{18}}\;rad\;$ de sa position d'équilibre stable et lâché sans vitesse initiale, nous évaluons la vitesse angulaire par « Regressi » selon le mode opératoire décrit ci-après « dans le menu “Grandeurs” du fichier, sélectionner “Tableau”, cliquer sur “ajouter (une colonne)” puis sélectionner “dérivée” en renseignant tout ce qui est demandé, une fois la colonne de vitesse angulaire établie aller dans le menu “Graphe” du fichier, sélectionner le tracé de la vitesse angulaire en fonction du temps, on visualise alors le diagramme horaire de vitesse angulaire $\;{\big (}$sans que les différents points successifs ne soient reliés${\big )}$, terminer en faisant la sauvegarde du fichier sous le nom “PPA_t_theta_omega.rw3” » $\;{\big [}$tracé non fourni, il est légèrement triangularisé avec une 1^ère pseudo-amplitude $\simeq 40\,{\text{°}}\cdot s^{-1}{\big ]}$.
• Portrait de phase du P.P.A. : à partir du fichier « PPA_t_theta_omega.rw3 » ouvert dans « Regressi » correspondant à l'acquisition des positions angulaires du P.P.A. écarté de $\;\theta _{0}\simeq 10\;{\text{°}}$ $\simeq +{\dfrac {\pi }{18}}\;rad\;$ de sa position d'équilibre stable et lâché sans vitesse initiale, à laquelle a été ajoutée l'évaluation de la vitesse angulaire correspondant aux différents instants de l'acquisition, on peut visualiser le portrait de phase du P.P.A. $\;{\big (}$sans que les différents points successifs ne soient reliés${\big )}\;$ selon le mode opératoire suivant « dans le menu “Graphe” du fichier, sélectionner l'élongation angulaire comme abscisse et la vitesse angulaire comme ordonnée » $\;{\big [}$tracé non fourni à allure de « patatoïde » $\;{\big (}$car les points ne sont pas reliés, la théorie conduisant à un portrait de phase spiralant en direction du point asymptote $\;\left\lbrace 0\,,\,0\right\rbrace {\big )}{\big ]}$.

Mise en évidence de l’amortissement du P.P.

     On observe pratiquement un amortissement exponentiel dans le diagramme horaire de position angulaire du P.P.A. du paragraphe « utilisation de la centrale de conversion Eurosmart SysamSP5 pilotée par l'interface python » plus haut dans ce chapitre bien que l'amplitude initiale d'oscillations ne soit pas petite $\;{\big (}$elle vaut en effet $\;\simeq 1,5\;rad\simeq 86\;{\text{°}}{\big )}$, la pseudo-période valant $\;{\mathcal {T}}\simeq 1,19\;s\;$ et, en supposant que la pseudo-amplitude $\;\searrow \;$ exponentiellement, le décrément logarithmique $\;\delta =\ln \!\left[{\dfrac {\theta (t)}{\theta (t+{\mathcal {T}})}}\right]={\dfrac {1}{n}}\;\ln \!\left[{\dfrac {\theta (t)}{\theta (t+n\;{\mathcal {T}})}}\right]\;$ est estimée à «$\;\delta \simeq 0,15\;$» d'où l'évaluation de la constante de temps d'amortissement $\;\tau ={\dfrac {\mathcal {T}}{\delta }}\simeq 7,9\;s$ $\;{\bigg [}$ceci, dans la mesure où la « pseudo-amplitude $\;\searrow \;$ selon $\;\exp \!\left(-{\dfrac {t}{\tau }}\right)\;$» $\Rightarrow$ $\;\delta ={\dfrac {\mathcal {T}}{\tau }}{\bigg ]}$.

     Dans le diagramme horaire de position angulaire du P.P.A. du paragraphe « autre utilisation de la centrale de conversion Eurosmart SysamSP5 associée aux logiciels “Synchronie 2003” et “Regressi” » plus haut dans ce chapitre, la $\;\searrow \;$ exponentielle de la pseudo-amplitude est établie algébriquement car cette dernière reste petite $\;{\big (}$la 1^ère pseudo-amplitude valant $\;10,1\;{\text{°}}{\big )}$, revoir l'étude dans le paragraphe précité $\;\ldots$

En complément : équation différentielle du mouvement du pendule pesant amorti (à un degré de liberté)

C.I. de lancement pour que le mouvement du P.P.A. soit à un degré de liberté

     Le pendule pesant $\;{\big (}$P.P.${\big )}\;$ devient « amorti $\;{\big (}$A.${\big )}\;$» s’il est soumis $\;{\big (}$en plus de son poids et des actions de la liaison en $\;O{\big )}\;$ à des forces de frottements fluides linéaires, les frottements solides étant toujours considérés comme inexistants :

• si la liaison est une liaison pivot $\;{\big (}$idéale${\big )}$, celle-ci imposant un seul degré de liberté de rotation, les C.I. de lancement peuvent être quelconques $\;{\big [}$toutefois la liaison n'autorise qu'une vitesse initiale de lancement $\;\perp \;$ à l'axe de la liaison${\big ]}$ ;

• si la liaison est une liaison sphérique pour laquelle existent trois degrés de liberté de rotation, les C.I. de lancement sont les mêmes que celles d'un P.P.N.A. permettant à ce dernier d'avoir un mouvement dans un plan fixe à savoir :
  $\;\succ \;$« on écarte le P.P.A. de sa position d’équilibre stable et on le lâche sans vitesse initiale $\;\left(C.I.\;{\mathfrak {a}}\right)\;$» ou
  $\;\succ \;$« on écarte le P.P.A. de sa position d’équilibre stable et on le lâche avec une vitesse initiale de son C.D.I. située dans le plan vertical contenant $\;O\;\left(C.I.\;{\mathfrak {b}}\right)\;$».

     Remarque : dans le cas où la liaison est une liaison pivot $\;{\big (}$idéale${\big )}$, les C.I. de lancement sont aussi les «$\;\left(C.I.\;{\mathfrak {a}}\right)\;$ ou $\;\left(C.I.\;{\mathfrak {b}}\right)\;$», la liaison pivot imposant que le C.D.I. $\;G\;$ ne peut être lancé que dans un plan transversal à la liaison $\;\ldots$

Dans le cas d’une liaison sphérique et avec les C.I. de lancement (C.I. a) ou (C.I. b), établissement de la nature plane du mouvement du C.D.I. G du P.P.A.

Schéma d'un P.P.A. à liaison sphérique avec ajout des actions extérieures, repérage cylindro-polaire d'axe $\;{\overrightarrow {Oz}}\;$ vertical descendant du C.D.I. $\;G\;$ du pendule, $\;I\;$ étant le point où la résultante des forces de frottement fluide peut être appliquée

     La démonstration est analogue à celle exposée pour établir la nature plane du mouvement du P.P.S.A. lancé dans les C.I. «$\;1a\;$» ou «$\;1b\;$» dans le paragraphe « en complément, établissement de la nature plane du mouvement du P.P.S.A. lancé dans les C.I. “1a” ou “1b” » du chap.$12$ de la leçon « Mécanique 1 (PCSI) », toutefois, nécessitant de légères modifications, elle est exposée ci-dessous :

     les actions extérieures exercées sur le pendule sont $\;{\big (}$voir schéma ci-contre${\big )}$

• son poids «$\;m\;{\vec {g}}=m\;g\;{\vec {u}}_{z}\;$» de moment vectoriel par rapport à $\;O\;$ «$\;{\overrightarrow {\mathcal {M}}}_{\!O}\!\left[m\;{\vec {g}}\right](t)=-m\;g\;{\mathfrak {a}}\;\sin \!\left[\theta _{G}(t)\right]\;{\vec {u}}_{\varphi _{G}}(t)\;$»,
• les actions de la liaison sphérique en $\;O\;$ se réduisant à « la réaction $\;{\vec {R}}(t)=R_{\rho _{G}}(t)\;{\vec {u}}_{\rho _{G}}(t)+R_{\varphi _{G}}(t)\;{\vec {u}}_{\varphi _{G}}(t)+R_{z}(t)\;{\vec {u}}_{z}\;$ appliquée en $\;O\;$» de vecteur moment par rapport à $\;O\;$ «$\;{\overrightarrow {\mathcal {M}}}_{\!O}\!\left[{\vec {R}}(t)\right]={\vec {0}}\;$» et
• les actions des « forces de frottement fluide » supposées « linéaires » : un pseudo point centré en $\;M\;$ de la surface latérale du front du P.P.A. de maître couple d'aire $\;{dS'}_{\!\!M}\;$ subissant une force de frottement fluide linéaire «$\;{\overrightarrow {d{\mathcal {R}}}}_{dS,\,{\text{flu}}}(M)=-h\;{\vec {V}}_{M}\;{\dfrac {{dS'}_{\!\!M}}{S'}}\;$» où «$\;S'=$ $\;\displaystyle \iint \limits _{S_{\text{lat. front}}}{dS'}_{\!\!M}\;$» est l'aire du maître couple du P.P.A. $\;{\big (}$en toute rigueur le front de la surface latérale dépend du sens de déplacement du pendule et par suite $\;{dS'}_{\!M}\;$ ainsi que $\;S'\;$ en dépendent, nous supposerons néanmoins, pour simplifier l'étude, qu'il n'en est rien${\big )}$, «$\;h\;$» étant une constante positive $\;{\big (}$exprimée en $\;kg\cdot s^{-1}{\big )}\;$ caractérisant le frottement linéaire et dépendant de la viscosité dynamique et de la densité du fluide ainsi que « de la forme et des dimensions du système de points matériels », on en déduit la résultante des forces de frottement fluide «$\;{\overrightarrow {\mathcal {R}}}_{\!{\text{flu}}}=\displaystyle \iint \limits _{S_{\text{lat. front}}}{\overrightarrow {d{\mathcal {R}}}}_{dS,\,{\text{flu}}}(M)=-{\dfrac {h}{S'}}\!\displaystyle \iint \limits _{S_{\text{lat. front}}}{\vec {V}}_{\!M}\;{dS'}_{\!\!M}\;$» ou, en définissant $\;I$, point solidaire du pendule, selon «$\;{\overrightarrow {OI}}={\dfrac {1}{S'}}\!\displaystyle \iint \limits _{S_{\text{lat. front}}}{\overrightarrow {OM}}\;{dS'}_{\!\!M}\;$» et en dérivant par rapport au temps «$\;{\vec {V}}_{I}(t)={\dfrac {1}{S'}}\!\displaystyle \iint \limits _{S_{\text{lat. front}}}{\vec {V}}_{\!M}(t)\;{dS'}_{\!\!M}\;$», la résultante des forces de frottement fluide peut se réécrire «$\;{\overrightarrow {\mathcal {R}}}_{\!{\text{flu}}}(t)=-h\;{\vec {V}}_{I}(t)\;$», résultante s’appliquant en «$\;I\;$» $\;\notin \;$ a priori au plan vertical contenant $\;{\overrightarrow {OG}}\;$ ;
       on en déduit le vecteur moment par rapport à $\;O\;$ des forces de frottement fluide «$\;{\overrightarrow {\mathcal {M}}}_{O,\,{\text{flu}}}={\overrightarrow {OI}}\wedge {\overrightarrow {\mathcal {R}}}_{\!{\text{flu}}}=-h\;{\overrightarrow {OI}}\wedge \left[{\vec {\Omega }}\wedge {\overrightarrow {OI}}\right]\;$» soit, en utilisant une formule du double produit vectoriel, «$\;{\overrightarrow {\mathcal {M}}}_{O,\,{\text{flu}}}$ $=-h\left[{\overrightarrow {OI}}^{2}\;{\vec {\Omega }}-\left({\overrightarrow {OI}}\cdot {\vec {\Omega }}\right){\overrightarrow {OI}}\right]\;$» ; sachant qu'avec les C.I. de lancement «$\;I\;$ $\in \;$ au plan vertical contenant $\;{\overrightarrow {OG}}\;$» d'une part et en faisant l'hypothèse que «$\;\theta _{I}=\theta _{G}\;$» d'autre part, on peut réécrire le vecteur rotation instantanée sous la forme unique «$\;{\vec {\Omega }}={\dot {\theta }}_{G}\;{\vec {u}}_{\varphi _{G}}+{\dot {\varphi }}_{G}\;{\vec {u}}_{z}\;$» et, avec «$\;{\overrightarrow {OI}}=r_{I}\;{\vec {u}}_{r_{G}}\;$», expliciter «$\;{\overrightarrow {OI}}\cdot {\vec {\Omega }}={\cancel {r_{I}\;{\dot {\theta }}_{G}\left({\vec {u}}_{r_{G}}\cdot {\vec {u}}_{\varphi _{G}}\right)+}}\;r_{I}\;{\dot {\varphi }}_{G}\left({\vec {u}}_{r_{G}}\cdot {\vec {u}}_{z}\right)=$ $r_{I}\;{\dot {\varphi }}_{G}\;\cos(\theta _{G})\;$», on obtient «$\;{\overrightarrow {\mathcal {M}}}_{O,\,{\text{flu}}}=-h\;r_{I}^{2}\left\lbrace {\dot {\theta }}_{G}\;{\vec {u}}_{\varphi _{G}}+{\dot {\varphi }}_{G}\left[{\vec {u}}_{z}-\cos(\theta _{G})\;{\vec {u}}_{r_{G}}\right]\right\rbrace \;$» ou encore, en posant «$\;H=h\,r_{I}^{2}\;$», «${\overrightarrow {\mathcal {M}}}_{O,\,{\text{flu}}}(t)=-H\;{\dot {\theta }}_{G}(t)\;{\vec {u}}_{\varphi _{G}}(t)-H\;{\dot {\varphi }}_{G}(t)\left\lbrace \sin ^{2}\!\left[\theta _{G}(t)\right]\;{\vec {u}}_{z}-\sin \!\left[\theta _{G}(t)\right]\;\cos \!\left[\theta _{G}(t)\right]\;{\vec {u}}_{\rho _{G}}(t)\right\rbrace$».

     Démonstration de la nature plane du mouvement de $\;G\;$ dans les $\;\left(C.I.\;{\mathfrak {a}}\right)\;$ de lancement : le théorème du mouvement du C.D.I. appliqué au P.P.A. $\Rightarrow$ «$\;m\;{\vec {g}}+{\vec {R}}(t)+{\overrightarrow {\mathcal {R}}}_{\!{\text{flu}}}(t)=m\;{\vec {a}}_{G}(t)\;\;({\mathfrak {2}})\;$» avec «$\;m\;{\vec {g}}\;$ et $\;{\vec {R}}\;$ dans le plan $\;\left({\vec {u}}_{\rho _{G}}\,,\,{\vec {u}}_{z}\right)\;$» d'une part ainsi que «$\;{\overrightarrow {\mathcal {R}}}_{\!{\text{flu}}}=-h\;{\vec {V}}_{I}=$ $-h\left[{\vec {\Omega }}\wedge {\overrightarrow {OI}}\right]=-h\left[{\dot {\theta }}_{G}\;{\vec {u}}_{\varphi _{G}}+{\dot {\varphi }}_{G}\;{\vec {u}}_{z}\right]\wedge r_{I}\;{\vec {u}}_{r_{G}}=-h\;r_{I}\left[{\dot {\theta }}_{G}\;{\vec {u}}_{\theta _{G}}+{\dot {\varphi }}_{G}\;\sin(\theta _{G})\;{\vec {u}}_{\varphi _{G}}\right]\;$» soit «$\;{\overrightarrow {\mathcal {R}}}_{\!{\text{flu}}}=$ $-h\;r_{I}\;{\dot {\theta }}_{G}\;{\vec {u}}_{\theta _{G}}-h\;\rho _{I}\;{\dot {\varphi }}_{G}\;{\vec {u}}_{\varphi _{G}}\;$ avec $\;r_{I}\;\sin(\theta _{G})=\rho _{I}\;$» d'autre part, d'où, en projetant sur $\;{\vec {u}}_{\varphi _{G}}$, l'équation suivante «$\;0+0-h\;\rho _{I}(t)\;{\dot {\varphi }}_{G}(t)=m\;a_{\varphi _{G},\,G}(t)\;$» ou, à l'aide de la forme semi-intégrée de l'accélération orthoradiale en repérage cylindro-polaire «$\;a_{\varphi _{G},\,G}(t)={\dfrac {1}{\rho _{G}(t)}}\;{\dfrac {d\!\left[\rho _{G}^{2}\,{\dot {\varphi _{G}}}\right]}{dt}}(t)\;$» dont la validité suppose «$\;\rho _{G}\neq 0\;$»,
     Démonstration de la nature plane du mouvement de $\;\color {transparent}{G}\;$ dans les $\;\color {transparent}{\left(C.I.\;{\mathfrak {a}}\right)}\;$ de lancement : «$\;-h\;\rho _{I}(t)\;{\dot {\varphi }}_{G}(t)={\dfrac {m}{\rho _{G}(t)}}\;{\dfrac {d\!\left[\rho _{G}^{2}\,{\dot {\varphi _{G}}}\right]}{dt}}(t)\;$ avec $\;\rho _{I}(t)={\dfrac {r_{I}}{\mathfrak {a}}}\;\rho _{G}(t)\;$» soit encore, en multipliant les deux membres par $\;\rho _{G}(t)\neq 0,\;\;\forall \;t$, la réécriture de l'équation selon $\;-h\;{\dfrac {r_{I}}{\mathfrak {a}}}\;\rho _{G}^{2}(t)\;{\dot {\varphi }}_{G}(t)=m\;{\dfrac {d\!\left[\rho _{G}^{2}\,{\dot {\varphi _{G}}}\right]}{dt}}(t)\;$ soit finalement l'équation différentielle suivante

«$\;{\dfrac {d\!\left[\rho _{G}^{2}\,{\dot {\varphi _{G}}}\right]}{dt}}(t)+{\dfrac {h\;r_{I}}{m\;{\mathfrak {a}}}}\left[\rho _{G}^{2}\,{\dot {\varphi _{G}}}\right](t)=0\;$ pour $\;t\in \mathbb {R} ^{+}\setminus \left\lbrace t_{\text{éq stable}}\right\rbrace \;$»,

     Démonstration de la nature plane du mouvement de $\;\color {transparent}{G}\;$ dans les $\;\color {transparent}{\left(C.I.\;{\mathfrak {a}}\right)}\;$ de lancement : qui s'intègre, sur chaque intervalle continu de temps ne contenant pas de valeurs $\;t_{\text{éq stable}}$, en «$\;\rho _{G}^{2}(t)\,{\dot {\varphi _{G}}}(t)=$ $A\;\exp \!\left(-{\dfrac {h\;r_{I}}{m\;{\mathfrak {a}}}}\;t\right)\;$» et
     Démonstration de la nature plane du mouvement de $\;\color {transparent}{G}\;$ dans les $\;\color {transparent}{\left(C.I.\;{\mathfrak {a}}\right)}\;$ de lancement : dont on peut prolonger le résultat aux valeurs discrètes $\;t_{\text{éq stable}}$ compte-tenu de la continuité des grandeurs $\;\rho _{G}(t)\;$ et $\;{\dot {\varphi _{G}}}(t)\;$ pour tout $\;t\in \mathbb {R}$, ce qui entraîne la continuité de $\;\rho _{G}^{2}(t)\,{\dot {\varphi _{G}}}(t)\;$ soit finalement

«$\;\rho _{G}^{2}(t)\,{\dot {\varphi _{G}}}(t)=A\;\exp \!\left(-{\dfrac {h\;r_{I}}{m\;{\mathfrak {a}}}}\;t\right)\!,\;\;\forall \;t\in \mathbb {R} ^{+}\;$» ;

     Démonstration de la nature plane du mouvement de $\;\color {transparent}{G}\;$ dans les $\;\color {transparent}{\left(C.I.\;{\mathfrak {a}}\right)}\;$ de lancement : on détermine la constante $\;A\;$ par utilisation partielle des C.I. $\;\left\lbrace {\begin{array}{l}\theta _{G}(0)=\theta _{0}\;&{\text{et }}&\varphi _{G}(0)=0\\{\dot {\theta _{G}}}(0)=0\;&{\text{et }}&{\dot {\varphi _{G}}}(0)=0\end{array}}\right\rbrace \;$ soit, avec «$\;\rho _{G}(t)={\mathfrak {a}}\;\sin \!\left[\theta _{G}(t)\right]\;$», la réécriture partielle des C.I. sous la forme «$\;{\mathfrak {a}}^{2}\;\sin ^{2}(\theta _{0})\;{\dot {\varphi _{G}}}(0)=A\;$» ou «$\;0=A\;$» et par suite

«$\;\rho _{G}^{2}(t)\,{\dot {\varphi _{G}}}(t)=0,\;\;\forall \;t\in \mathbb {R} ^{+}$» ou,

     Démonstration de la nature plane du mouvement de $\;\color {transparent}{G}\;$ dans les $\;\color {transparent}{\left(C.I.\;{\mathfrak {a}}\right)}\;$ de lancement : en simplifiant par $\;\rho _{G}^{2}(t)\;$ non identiquement nul,

«$\;{\dot {\varphi _{G}}}(t)=0,\;\;\forall \;t\in \mathbb {R} ^{+}$» ou enfin,

     Démonstration de la nature plane du mouvement de $\;\color {transparent}{G}\;$ dans les $\;\color {transparent}{\left(C.I.\;{\mathfrak {a}}\right)}\;$ de lancement : après intégration «$\;\varphi _{G}(t)=cste',\;\;\forall \;t\in \mathbb {R} ^{+}\;$», valeur de $\;cste'\;$ déterminée par C.I. $\;\varphi _{G}(0)=0$, soit finalement

«$\;\varphi _{G}(t)=0,\;\;\forall \;t\in \mathbb {R} ^{+}\;$»,
c'est-à-dire la nature plane du mouvement de $\;G\;$ dans le plan de lancement.

     Démonstration de la nature plane du mouvement de $\;G\;$ dans les $\;\left(C.I.\;{\mathfrak {b}}\right)\;$ de lancement : aucune modification avant l'intervention des C.I. $\Rightarrow$ «$\;\rho ^{2}(t)\,{\dot {\varphi }}(t)=A\;\exp \!\left(-{\dfrac {h\;r_{I}}{m\;{\mathfrak {a}}}}\;t\right)\!,\;\;\forall \;t\in \mathbb {R} ^{+}\;$» comme précédemment, la constante d'intégration se déterminant par utilisation partielle des C.I. $\;\left\lbrace {\begin{array}{l}\theta _{G}(0)=\theta _{0}\;&{\text{et }}&\varphi _{G}(0)=0\\{\dot {\theta _{G}}}(0)={\dfrac {V_{0}}{\mathfrak {a}}}\;&{\text{et }}&{\dot {\varphi _{G}}}(0)=0\end{array}}\right\rbrace \;$ soit, avec «$\;\rho _{G}(t)={\mathfrak {a}}\;\sin \!\left[\theta _{G}(t)\right]\;$», la réécriture partielle des C.I. sous la forme «$\;{\mathfrak {a}}^{2}\;\sin ^{2}(\theta _{0})\;{\dot {\varphi _{G}}}(0)=A\;$» ou «$\;0=A\;$» et par suite

«$\;\rho _{G}^{2}(t)\,{\dot {\varphi _{G}}}(t)=0,\;\;\forall \;t\in \mathbb {R} ^{+}$» ou,

     Démonstration de la nature plane du mouvement de $\;\color {transparent}{G}\;$ dans les $\;\color {transparent}{\left(C.I.\;{\mathfrak {b}}\right)}\;$ de lancement : en simplifiant par $\;\rho _{G}^{2}(t)\;$ non identiquement nul,

«$\;{\dot {\varphi _{G}}}(t)=0,\;\;\forall \;t\in \mathbb {R} ^{+}$» ou enfin,

     Démonstration de la nature plane du mouvement de $\;\color {transparent}{G}\;$ dans les $\;\color {transparent}{\left(C.I.\;{\mathfrak {b}}\right)}\;$ de lancement : après intégration «$\;\varphi _{G}(t)=cste',\;\;\forall \;t\in \mathbb {R} ^{+}\;$», valeur de $\;cste'\;$ déterminée par C.I. $\;\varphi _{G}(0)=0$, soit

«$\;\varphi _{G}(t)=0,\;\;\forall \;t\in \mathbb {R} ^{+}\;$»,
c'est-à-dire la nature plane du mouvement de $\;G\;$ dans le plan de lancement.

Dans le cas d’une « liaison pivot » ou d’une « liaison sphérique avec C.I. de lancement (C.I. a) ou (C.I. b) », nouveau repérage adapté à la nature rotatoire du mouvement du P.P.A. à un degré de liberté

Schéma d'un pendule pesant amorti à un degré de liberté, repérage polaire de son C.D.I. $\;G\;$ et représentation des forces extérieures, $\;I\;$ étant le point où la résultante des forces de frottement fluide peut être appliquée

     Avec les deux types de liaison, « liaison pivot » ou « liaison sphérique avec C.I. de lancement $\;\left(C.I.\;{\mathfrak {a}}\right)\;$ ou $\;\left(C.I.\;{\mathfrak {b}}\right)\;$», le P.P.A. ayant un mouvement de rotation autour d’un axe horizontal fixe noté $\;\Delta _{O}\;$ et orienté par «$\;{\vec {u}}_{\Delta _{O}}\;$»,
     on repère le C.D.I. $\;G\;$ du P.P.A. dans le plan vertical du mouvement $\;zOx$ $\;{\big \{}$avec $\;{\vec {u}}_{z}\;$ unitaire vertical descendant, $\;{\vec {u}}_{x}\;$ unitaire horizontal $\;\perp \;$ au 3^ème vecteur unitaire horizontal $\;{\vec {u}}_{y}={\vec {u}}_{\Delta _{O}}\;$ tels que la base cartésienne «$\;\left({\vec {u}}_{z}\,,\,{\vec {u}}_{x}\,,\,{\vec {u}}_{\Delta _{O}}\right)\;$ soit directe », l'espace physique étant orienté à droite${\big \}}$,
               on repère le C.D.I. $\;\color {transparent}{G}\;$ du P.P.A. par ses coordonnées polaires de pôle $\;O\;$ et d’axe $\;\Delta _{O}\;$ orienté par $\;{\vec {u}}_{\Delta _{O}}\;$ soit, avec la base polaire liée au C.D.I. $\;G\;$ du P.P.A. dans ce plan $\;zOx$, «$\;\left({\vec {u}}_{r}\,,\,{\vec {u}}_{\theta }\right)\;$», «$\;\left\lbrace r_{G}={\mathfrak {a}}\,,\,\theta _{G}={\widehat {\left({\vec {u}}_{z}\,,\,{\overrightarrow {OG}}\right)}}={\widehat {\left({\vec {u}}_{z}\,,\,{\vec {u}}_{r}\right)}}\right\rbrace \;$», «$\;\theta _{G}\;$» $\;{\big [}$abscisse angulaire du C.D.I. $\;G\;$ du P.P.A. noté «$\;\theta \;$» par la suite en absence d'ambiguïté${\big ]}\;$ est aussi le paramètre de position angulaire utilisé pour repérer le mouvement du P.P.A. $\;{\big [}$ici nous considérons que le front de la surface latérale du P.P.A. ne dépend pas du sens de déplacement de ce dernier et par suite que le point d'application $\;I\;$ de la résultante des forces de frottement fluide n'en dépend pas non plus en étant, d'une part, « dans le plan vertical du mouvement de $\;G\;$» et, d'autre part, « sur le support de $\;{\overrightarrow {OG}}\;$»${\big ]}$.

     Les actions extérieures agissant sur le P.P.A. représentées sur le schéma ci-contre sont les seules dans l'hypothèse d'une « liaison sphérique avec C.I. de lancement $\;\left(C.I.\;{\mathfrak {a}}\right)\;$ ou $\;\left(C.I.\;{\mathfrak {b}}\right)\;$», mais $\;\ldots$
           Les actions extérieures agissant sur le P.P.A. représentées sur le schéma ci-contre sont les seules dans celle d'une « liaison pivot » il faudrait ajouter le couple de réaction du pivot de moment vectoriel $\;{\vec {\Gamma }}_{{\text{pendule}}\,\leftarrow \,{\text{pivot}}}\;\perp \;$ à $\;\Delta _{O}$ $\;{\big [}$on rappelle qu'un couple n'est pas représenté par son moment mais par le sens de rotation qu'il engendrerait s'il agissait seul en mettant, à côté de la flèche incurvée précisant le sens, le nom du vecteur moment du couple, ici ce n'est pas fait car ce couple n'interviendra pas dans l'application du théorème de la dynamique permettant d'obtenir l'équation différentielle en $\;\theta (t)\;$ du P.P.A.${\big ]}$.

Établissement de l’équation différentielle du mouvement du P.P.A. à un degré de liberté

     $\;\Delta _{O}\;$ étant un axe fixe dans le référentiel d’étude $\;{\mathcal {R}}\;$ galiléen, on peut appliquer au P.P.A. à un degré de liberté le théorème du moment cinétique scalaire par rapport à l’axe $\;\Delta _{O}$, les actions extérieures s'exerçant sur le pendule étant :

• son poids «$\;m\;{\vec {g}}=m\;g\;{\vec {u}}_{z}\;$» de moment scalaire par rapport à $\;\Delta _{O}\;$ «$\;{\mathcal {M}}_{\!\Delta _{O}}\!\left[m\;{\vec {g}}\right](t)=\left[{\overrightarrow {OG}}(t)\wedge m\;{\vec {g}}\right]\cdot {\vec {u}}_{\Delta _{O}}=-m\;g\;{\mathfrak {a}}\;\sin \!\left[\theta (t)\right]\;$»,
• la réaction du point $\;O\;$ de la liaison sphérique sur le pendule lancé dans les C.I. $\;\left(C.I.\;{\mathfrak {a}}\right)\;$ ou $\;\left(C.I.\;{\mathfrak {b}}\right)$, «$\;{\vec {R}}(t)=R_{r}(t)\;{\vec {u}}_{r}(t)+R_{\theta }(t)\;{\vec {u}}_{\theta }(t)\;$» de moment scalaire «$\;{\mathcal {M}}_{\!\Delta _{O}}\!\left[{\vec {R}}(t)\right]=0\;$» ou
  la réaction de l'axe $\;\Delta _{O}\;$ de la liaison pivot sur le pendule lancé avec n'importe quelles C.I. compatibles avec la liaison, «$\;{\vec {R}}(t)=R_{r}(t)\;{\vec {u}}_{r}(t)+R_{\theta }(t)\;{\vec {u}}_{\theta }(t)\;$» de moment scalaire «$\;{\mathcal {M}}_{\!\Delta _{O}}\!\left[{\vec {R}}(t)\right]$ $=0\;$» auquel s'ajoute le couple de réaction du pivot de moment vectoriel $\;{\vec {\Gamma }}_{{\text{pendule}}\,\leftarrow \,{\text{pivot}}}={\overline {\Gamma _{{\text{pendule}}\,\leftarrow \,{\text{pivot}},\,r}}}\;{\vec {u}}_{r}+{\overline {\Gamma _{{\text{pendule}}\,\leftarrow \,{\text{pivot}},\,\theta }}}\;{\vec {u}}_{\theta }\;$ et par suite de moment scalaire relativement à $\;\Delta _{O}\;$ «$\;{\overline {\Gamma _{{\text{pendule}}\,\leftarrow \,{\text{pivot}},}}}_{\Delta _{O}}=0\;$»,
• la résultante des forces de frottement fluide linéaire «$\;{\overrightarrow {\mathcal {R}}}_{\!{\text{flu}}}(t)=-h\;{\vec {V}}_{I}(t)\;{\overset {\cdots }{\,=\,}}-h\;r_{I}\left\lbrace {\dot {\theta }}_{G}(t)\;{\vec {u}}_{\theta _{G}}(t)\;{\cancel {+\;{\dot {\varphi }}_{G}(t)\;\sin \!\left[\theta _{G}(t)\right]\,{\vec {u}}_{\varphi _{G}}(t)}}\right\rbrace \;$» dont le moment vectoriel évalué relativement à $\;O\;$ étant «$\;{\overrightarrow {\mathcal {M}}}_{O,\,{\text{flu}}}(t)$ $={\overrightarrow {OI}}(t)\wedge {\overrightarrow {\mathcal {R}}}_{\!{\text{flu}}}(t)\;{\overset {\cdots }{\,=\,}}-h\;r_{I}^{2}\left[{\dot {\theta }}_{G}(t)\;{\vec {u}}_{\varphi _{G}}\;{\cancel {+\;{\dot {\varphi }}_{G}(t)\left\lbrace {\vec {u}}_{z}-\cos \!\left[\theta _{G}(t)\right]{\vec {u}}_{r_{G}}(t)\right\rbrace }}\right]\;$» permet de déduire le moment scalaire relativement à $\;\Delta _{O}$ $\;{\big (}$sachant que $\;{\vec {u}}_{\varphi _{G}}\;$ s'identifie à $\;{\vec {u}}_{\Delta _{O}}{\big )}\;$ «$\;{\mathcal {M}}_{\!\Delta _{O},\,{\text{flu}}}(t)={\overrightarrow {\mathcal {M}}}_{O,\,{\text{flu}}}(t)\cdot {\vec {u}}_{\Delta _{O}}=-h\;r_{I}^{2}\;{\dot {\theta }}_{G}(t)\;$» soit, en posant $\;H=h\;r_{I}^{2}\;$ et en remplaçant $\;\theta _{G}\;$ par $\;\theta \;$ en absence d'ambigüité, «$\;{\mathcal {M}}_{\!\Delta _{O},\,{\text{flu}}}(t)=-H\;{\dot {\theta }}(t)\;$» ;

     l'application du théorème du moment cinétique scalaire au P.P.A. en rotation autour de l'axe $\;\Delta _{O}$, fixe dans le référentiel d'étude $\;{\mathcal {R}}\;$ galiléen, avec la vitesse angulaire $\;{\dot {\theta }}(t)\;$ à l'instant $\;t$, s'écrit

«$\;{\mathcal {M}}_{\!\Delta _{O}}\!\left[m\;{\vec {g}}\right](t)+{\mathcal {M}}_{\!\Delta _{O}}\!\left[{\vec {R}}(t)\right]+{\mathcal {M}}_{\!\Delta _{O},\,{\text{flu}}}(t)=J_{\Delta _{O}}\;{\ddot {\theta }}(t)\;$» dans le cas d'un P.P.A. à un degré de liberté, lié à $\;O\;$ par « liaison sphérique » ou
«$\;{\mathcal {M}}_{\!\Delta _{O}}\!\left[m\;{\vec {g}}\right](t)+{\mathcal {M}}_{\!\Delta _{O}}\!\left[{\vec {R}}(t)\right]+{\overline {\Gamma _{{\text{pendule}}\,\leftarrow \,{\text{pivot}},}}}_{\Delta _{O}}+{\mathcal {M}}_{\!\Delta _{O},\,{\text{flu}}}(t)=J_{\Delta _{O}}\;{\ddot {\theta }}(t)\;$» dans le cas d'un P.P.A. lié à $\;\Delta _{O}\;$ par « liaison pivot »,
«$\;J_{\Delta _{O}}\;$ étant le moment d'inertie du P.P.A. relativement à $\;\Delta _{O}\;$» et
«$\;{\ddot {\theta }}(t)\;$ l'accélération angulaire du P.P.A. à l'instant $\;t\;$» soit

     en remplaçant les moments scalaires par leur expression précédemment déterminée,

«$\;-m\;g\;{\mathfrak {a}}\;\sin \!\left[\theta (t)\right]+0-H\;{\dot {\theta }}(t)=J_{\Delta _{O}}\;{\ddot {\theta }}(t)\;$» dans le cas d'un P.P.A. à un degré de liberté, lié à $\;O\;$ par « liaison sphérique » ou
«$\;-m\;g\;{\mathfrak {a}}\;\sin \!\left[\theta (t)\right]+0+0-H\;{\dot {\theta }}(t)b=J_{\Delta _{O}}\;{\ddot {\theta }}(t)\;$» dans le cas d'un P.P.A. lié à $\;\Delta _{O}\;$ par « liaison pivot » ou encore,

     en normalisant l'équation différentielle en $\;\theta (t)\;$ du mouvement du P.P.A.

«$\;{\ddot {\theta }}(t)+{\dfrac {H}{J_{\Delta _{O}}}}\;{\dot {\theta }}(t)+{\dfrac {m\;g\;{\mathfrak {a}}}{J_{\Delta _{O}}}}\;\sin \!\left[\theta (t)\right]=0\;$» soit
une équation différentielle non linéaire du 2^ème ordre en $\;\theta (t)\;$ avec terme linéaire du 1^er ordre,
caractérisant un oscillateur non linéaire amorti dans la mesure où le mouvement reste pseudo-oscillatoire.

Absence de solution analytique dans le cas général d’amplitudes initiales non petites

     Comme l’équation différentielle en $\;\theta (t)\;$ du P.P.A. est de même nature que celle du « P.P.S.A.  », on peut faire les mêmes commentaires, rappelés ci-après :

     l’équation différentielle non linéaire du 2^ème ordre en $\;f(x)$ $\;{\big (}$sans terme du 1^er ordre${\big )}$ $\;{\dfrac {d^{2}f}{dx^{2}}}(x)+k\;\sin \!\left[f(x)\right]=0\;$ n'ayant pas de solution analytique, l'ajout d’un terme supplémentaire d’amortissement du 1^er ordre dans une telle équation différentielle ne peut pas rendre cette dernière soluble analytiquement, on conclut donc à

l’absence de résolution analytique exacte de l’équation différentielle du P.P.A.,

     la seule possibilité est une résolution approchée

• analytique dans le cas d’« élongations angulaires petites » $\;{\big [}$voir ci-dessous à la fin de ce paragraphe${\big ]}\;$ ou
• numérique dans le cas général d’« élongations angulaires non petites » $\;{\big [}$résolution analogue à celle présentée au paragraphe « en complément, résolution numérique de l'équation différentielle d'un P.P.S. dans les C.I. 1a puis 1b, tracé des diagrammes horaires de position et de vitesse ainsi que celui des portraits de phase correspondant » du chap.$12$ de la leçon « Mécanique 1 (PCSI) » nécessitant néanmoins d'ajouter le terme d'amortissement$\;\ldots {\big ]}$.

     Résolution analytique approchée de l'équation différentielle du P.P.A. dans le cas des petites élongations angulaires : Le plus simple pour être dans le cadre des « petites élongations angulaires » est de lancer le P.P.A. avec les C.I. de lancement particulières $\;{\big (}$que la liaison avec $\;O\;$ ou $\;\Delta _{O}\;$ soit sphérique ou pivot${\big )}$ suivantes :

                  Résolution analytique approchée de l'équation différentielle du P.P.A. dans le cas des petites élongations angulaires :« on écarte le P.P.A. de sa position d’équilibre stable et on le lâche sans vitesse initiale » en supposant l’abscisse angulaire initiale $\;\theta _{0}\;$ de valeur absolue petite c'est-à-dire $\;\vert \theta _{0}\vert \ll 1\;$, l'absence de vitesse angulaire initiale assurant que « la valeur absolue de l'élongation angulaire ne dépassera pas $\;\vert \theta _{0}\vert \;$» et restera petite soit «$\;\vert \theta (t)\vert \ll 1\;\;\forall \;t\;$ » ;

                  Résolution analytique approchée de l'équation différentielle du P.P.A. dans le cas des petites élongations angulaires :dans le cadre des « petites élongations angulaires » on a $\;\vert \theta (t)\vert \ll \;\;\forall \;t\;$ permettant d'effectuer un D.L. à l'ordre un en $\;\theta \;$ de $\;\sin(\theta )\;$ au voisinage de 0 selon $\;\sin(\theta )\simeq \theta \;$ à l'ordre un en $\;\theta \;$ et par suite l'équation différentielle suivie par le P.P.A. devient linéaire selon

«$\;{\ddot {\theta }}(t)+{\dfrac {H}{J_{\Delta _{O}}}}\;{\dot {\theta }}(t)+{\dfrac {m\;g\;{\mathfrak {a}}}{J_{\Delta _{O}}}}\;\theta (t)\simeq 0\;$»

                  Résolution analytique approchée de l'équation différentielle du P.P.A. dans le cas des petites élongations angulaires :c'est-à-dire une équation différentielle linéaire à cœfficients constants du 2^ème ordre en $\;\theta (t)\;$ avec terme d'amortissement et homogène.

                  Résolution analytique approchée de l'équation différentielle du P.P.A. dans le cas des petites élongations angulaires :Le P.P.A. est donc linéarisable dans l'hypothèse des « petites élongations angulaires » et dans cette hypothèse il devient un « oscillateur harmonique $\;{\big (}$amorti${\big )}\;$ » de pulsation propre «$\;\omega _{0}={\sqrt {\dfrac {m\;g\;{\mathfrak {a}}}{J_{\Delta _{O}}}}}\;$» appelée « pulsation $\;{\big (}$propre${\big )}\;$ des petites élongations angulaires » et de facteur d’amortissement «$\;\sigma \;$» tel que «$\;{\dfrac {H}{J_{\Delta _{O}}}}=2\;\sigma \;\omega _{0}\;$» ou «$\;\sigma ={\dfrac {H}{2\;J_{\Delta _{O}}\;\omega _{0}}}={\dfrac {H}{2\;{\sqrt {m\;g\;{\mathfrak {a}}\;J_{\Delta _{O}}}}}}\;$» d’où

• si «$\;\sigma \;$ est $\;<\;$ à $\;1\;$» le régime est pseudo-périodique de pseudo-pulsation des petites oscillations «$\;\omega =\omega _{0}\;{\sqrt {1-\sigma ^{2}}}\;$», l’amortissement étant exponentiel en «$\;\exp \!\left(-\sigma \;\omega _{0}\;t\right)\;$» $\;{\big [}$de même forme que celle établie au paragraphe « σ < 1 (faible amortissement) et réponse pseudo-périodique » du chap.$28$ de la leçon « Signaux physiques (PCSI) »${\big ]}$,
• si «$\;\sigma \;$ est $\;=\;$ à $\;1\;$» le régime est apériodique critique $\;{\big [}$de même forme que celle établie au paragraphe « σ = 1 (amortissement critique) et réponse apériodique critique » du chap.$28$ de la leçon « Signaux physiques (PCSI) »${\big ]}\;$ et
• si «$\;\sigma \;$ est $\;>\;$ à $\;1\;$» le régime est apériodique $\;{\big [}$de même forme que celle établie au paragraphe « σ > 1 (fort amortissement) et réponse apériodique » du chap.$28$ de la leçon « Signaux physiques (PCSI) »${\big ]}\;$ $\;\ldots$

Rappel du cas particulier : pendule pesant simple (non amorti à un degré de liberté) utilisant une tige rigide sans masse, équilibres du pendule et notion de stabilité, généralisation aux équilibres d'un solide en rotation autour d’un axe fixe ainsi que de leur stabilité ou instabilité

Rappel du cas particulier : P.P.S.(N.A. à un degré de liberté) construit à partir d’une tige rigide sans masse et un point matériel M

     Revoir le chap.$12$ « Loi de la quantité de mouvement : Pendule pesant simple » de la leçon « Mécanique 1 (PCSI) » dans lequel on trouve, dans les paragraphes successifs suivants :

• « la description et le cas limite du pendule pesant simple (P.P.S.), les conditions initiales induisant un mouvement à un degré de liberté avec établissement de la nature plane du mouvement »,
• « le choix, pour un P.P.S. à un degré de liberté, du repérage polaire de pôle “le centre du mouvement circulaire du P.P.S.” »,
• « la mise en équation d'un P.P.S. à un degré de liberté par application de la r.f.d.n. donnant une équation différentielle non linéaire du 2^ème ordre avec absence de solution analytique (et la nécessité d'une résolution numérique dans le cas général) » $\color {red}{\big (}$seul ce paragraphe sera repris en utilisant le théorème du moment cinétique scalaire, tout ce qui précède et tout ce qui suit, restant inchangés$\color {red}{\big )}$,
• « l'approximation linéaire, dans le cadre des “petites élongations angulaires”, du mouvement d'un P.P.S. à un degré de liberté, son analogie avec l'oscillateur harmonique et la période des “petites élongations angulaires” »,
• « la détermination de l'équation du portrait de phase (“intégrale 1^ère du mouvement”) dans le cas général du P.P.S. à un degré de liberté »,
• « les portraits de phase dans le cas général “d'oscillations ou de mouvement révolutif” d'un P.P.S. à un degré de liberté et dans le cas particuliers des petites élongations angulaires »,
• « en complément, l'absence d'isochronisme du P.P.S.(N.A.) à un degré de liberté et l'expression empirique de “de Borda” de la période dans le cas général d'oscillations » et
• « en complément, la “résolution numérique” d'un P.P.S. dans les C.I. “1a” puis “1b” avec le tracé des diagrammes horaires de position et de vitesse ainsi que celui des portraits de phase correspondant ».

     Revoir aussi le paragraphe « Étude énergétique d'un point matériel en mouvement conservatif à une dimension sur l'exemple du pendule pesant simple à un degré de liberté, diagramme d'énergies potentielle et mécanique, présence de deux murs d'énergie potentielle (positions de vitesse nulle) et trajectoire (cinétiquement) bornée, mouvement périodique et expression de la période sous forme intégrale, absence d'isochronisme des oscillations » du chap.$17$ de la leçon « Mécanique 1 (PCSI) » dans lequel on trouve, dans les sous paragraphes successifs suivants :

• « l'écriture de l'intégrale 1^ère énergétique du pendule pesant simple (P.P.S.) à un degré de liberté »,
• « le diagramme d'énergies potentielle et mécanique du P.P.S. à un degré de liberté lancé dans les conditions initiales (C.I.) “1a” »,
• « la présence de deux murs d'énergie potentielle ayant pour conséquence le caractère “cinétiquement borné” de la trajectoire du point matériel »,
• « la détermination de la nature oscillatoire du mouvement du P.P.S. à un degré de liberté “par diagramme énergétique” »,
• « la détermination de la nature périodique du mouvement du P.P.S. à un degré de liberté et l'expression de la période sous forme intégrale »,
• « l'absence d'isochronisme des oscillations »,
• « en complément, l'évaluation numérique de la période et la comparaison avec l'“expression approchée de de Borda” »,
• « le retour sur les petites élongations angulaires d'un P.P.S. à un degré de liberté en termes de diagramme d'énergies potentielle et mécanique » et
• « l'étude énergétique d'un P.P.S. à un degré de liberté dans des C.I. “1b” par diagramme d'énergies potentielle et mécanique » permettant de distinguer
  $\;\succ \;$« les conditions pour que le mouvement du P.P.S.N.A. soit oscillatoire »,
  $\;\succ \;$« les conditions pour que le mouvement du P.P.S.N.A. soit révolutif » et
  $\;\succ \;$« les conditions pour que le mouvement du P.P.S.N.A. s'arrête en une position d'équilibre instable ».

     Remarque : tout ayant été traité, nous ne reprendrons que la mise en équation que l’on fait ici par application du théorème du moment cinétique scalaire à $\;M$.

Détermination de l’équation différentielle en θ(t) par application du théorème du moment cinétique scalaire au point matériel M dans le cas d’un P.P.S.N.A.

Schéma d'un P.P.S.N.A. à un degré de liberté avec repérage cylindro-polaire d'axe $\;\Delta _{O}\;$ et représentation des deux forces s'appliquant sur le point $\;M\;$ du P.P.S.N.A.

     Le mouvement étant plan, dans le plan vertical contenant initialement la tige, plus exactement, en notant $\;\Delta _{O}\;$ l'axe passant par $\;O\;$ et $\;\perp \;$ au plan vertical initial, le mouvement de $\;M\;$ est circulaire d'axe $\;\Delta _{O}$ ;

     il devient alors intéressant d'utiliser le repérage cylindro-polaire d'axe $\;\Delta _{O}\;$ pour repérer le point $\;M\;$ ou, le repérage se faisant dans un plan, d'utiliser le repérage polaire de pôle $\;O\;$ et d'axe polaire $\;{\overrightarrow {Oz}}$ $\;{\big (}$le plan étant orienté par $\;{\vec {u}}_{\Delta _{O}}{\big )}$, les coordonnées polaires de $\;M\;$ étant «$\;\left({\mathit {l}}\,,\,\theta \right)\;$» et la base polaire du plan liée au point $\;M\;$ «$\;\left({\vec {u}}_{r}\,,\,{\vec {u}}_{\theta }\right)\;$», $\;\theta \;$ définissant l'angle polaire de $\;M$, angle orienté par $\;{\vec {u}}_{\!\Delta _{O}}$, voir ci-contre.

     Le mouvement du point $\;M\;$ étant entièrement décrit par la connaissance de la loi horaire «$\;\theta =\theta (t)\;$» dans laquelle «$\;\theta$, l'abscisse angulaire du point $\;M\;$ est le paramètre de position de ce dernier » et le mouvement du point $\;M\;$ étant circulaire autour d'un axe fixe dans un référentiel galiléen $\;{\mathcal {R}}$, la détermination de l'équation différentielle en $\;\theta (t)\;$ devrait être plus aisée en appliquant le théorème du moment cinétique scalaire au point $\;M\;$ dans le référentiel galiléen $\;{\mathcal {R}}$ ;

     le point $\;M\;$ est soumis à deux forces :

• une force à distance « le poids de $\;M\;$» «$\;m\;{\vec {g}}\;$» dont le moment scalaire par rapport à l'axe de rotation $\;\Delta _{O}\;$ s'écrit «$\;{\mathcal {M}}_{\!\Delta _{O}}\!\left[m\;{\vec {g}}\right](t)=\left[{\overrightarrow {OM}}(t)\wedge m\;{\vec {g}}\right]\cdot {\vec {u}}_{\Delta _{O}}=$ $-m\;g\;{\mathit {l}}\;\sin \!\left[\theta (t)\right]\;$» et
• une force de contact « la tension de la tige » «$\;{\vec {T}}(t)$ ${\big [}$a priori centripète mais pouvant être centrifuge pour des élongations angulaires obtus${\big ]}\;$» dont le moment scalaire par rapport à l'axe de rotation $\;\Delta _{O}\;$ vaut «$\;{\mathcal {M}}_{\!\Delta _{O}}\!\left[{\vec {T}}\right](t)=\left[{\overrightarrow {OM}}(t)\wedge {\vec {T}}(t)\right]\cdot {\vec {u}}_{\Delta _{O}}=0\;$» ;

     l'application du théorème du moment cinétique scalaire au P.P.S.N.A. en rotation autour de l'axe $\;\Delta _{O}$, fixe dans le référentiel d'étude $\;{\mathcal {R}}\;$ galiléen, avec la vitesse angulaire $\;{\dot {\theta }}(t)\;$ à l'instant $\;t$, s'écrit

«$\;{\mathcal {M}}_{\!\Delta _{O}}\!\left[m\;{\vec {g}}\right](t)+{\mathcal {M}}_{\!\Delta _{O}}\!\left[{\vec {T}}(t)\right]=J_{\Delta _{O}}(M)\;{\ddot {\theta }}(t)\;$» dans le cas d'un P.P.S.N.A. à un degré de liberté, lié à $\;O\;$ par « tige rigide inextensible »,
«$\;J_{\Delta _{O}}(M)\;$ étant le moment d'inertie du point matériel $\;M\,\left(m\right)\;$ relativement à $\;\Delta _{O}\;$» défini par $\;J_{\Delta _{O}}(M)=m\;{\mathit {l}}^{,2}\;$ où
$\;{\mathit {l}}\;$ est la distance orthogonale de $\;M\;$ à $\;O$ $\;{\big (}$c'est-à-dire la longueur de la tige${\big )}\;$ et
«$\;{\ddot {\theta }}(t)\;$ l'accélération angulaire du point matériel $\;M\,\left(m\right)\;$ à l'instant $\;t\;$» soit

     en remplaçant les moments scalaires par leur expression précédemment déterminée,

«$\;-m\;g\;{\mathit {l}}\;\sin \!\left[\theta (t)\right]+0=m\;{\mathit {l}}^{\,2}\;{\ddot {\theta }}(t)\;$» dans le cas d'un P.P.S.N.A. à un degré de liberté, lié à $\;O\;$ par « tige rigide inextensible » ou,

     en normalisant l'équation différentielle en $\;\theta (t)\;$ du mouvement du P.P.S.N.A.

«$\;{\ddot {\theta }}(t)+{\dfrac {g}{\mathit {l}}}\;\sin \!\left[\theta (t)\right]=0\;$» soit
une équation différentielle non linéaire du 2^ème ordre en $\;\theta (t)\;$ sans terme du 1^er ordre,
caractérisant un oscillateur non linéaire dans la mesure où le mouvement reste oscillatoire.

Rappel : équilibres du pendule pesant simple et notion de stabilité

     Revoir le paragraphe « définition de positions d'équilibre sur l'exemple du pendule pesant simple à un degré de liberté (P.P.S.), distinction entre “forces (ou composantes de forces) causes de modification du mouvement” et “forces (ou composantes de forces) sans influence sur une modification éventuelle du mouvement” » du chap.$18$ de la leçon « Mécanique 1 (PCSI) » pour la notion d'équilibre d'un P.P.S. et

     Revoir le paragraphe « définition de la stabilité ou de l'instabilité d'un équilibre de point matériel à un degré de liberté en termes de force, exemple du P.P.S. à un degré de liberté » du même chapitre de la même leçon pour la notion de stabilité $\;{\big (}$ou d'instabilité${\big )}\;$ d'un P.P.S..

     Retour sur la détermination des positions d'équilibre d'un P.P.S. : nous avons défini les abscisses angulaires d’équilibre par les zéros de la « force motrice » $\;{\big [}$plus exactement les zéros de la « composante de $\;m\;{\vec {g}}\;$ sur $\;{\vec {u}}_{\theta }\;$» à savoir «$\;F(\theta )=-m\;g\;\sin(\theta )\;$»${\big ]}$, l’équation différentielle ayant été obtenue en écrivant «$\;F\!\left[\theta (t)\right]=m\;a_{\theta }(t)\;$» et l’équilibre nécessitant «$\;a_{\theta }(t)=0\;\;\forall \;t\;$» ;

            Retour sur la détermination des positions d'équilibre d'un P.P.S. : comme nous pouvons déterminer l’équation différentielle par «$\;{\mathcal {M}}_{\!\Delta _{O}}\!\left[m\;{\vec {g}}\right](t)=J_{\Delta _{O}}(M)\;{\ddot {\theta }}(t)\;$» et que l’équilibre nécessite «$\;{\ddot {\theta }}(t)$ $=0\;\;\forall \;t\;$», les abscisses angulaires d’équilibre sont également les zéros du « moment scalaire moteur » à savoir

«$\;{\mathcal {M}}_{\!\Delta _{O},\,m\,{\vec {g}}}(\theta _{\text{éq}})=0\;$» ou «$\;-m\;g\;{\mathit {l}}\;\sin(\theta _{\text{éq}})=0\;$» soit «$\;\theta _{\text{éq}}=0$ ou $\pi \;$».

     Retour sur la détermination de la stabilité${\underline {\;(}}$ou de l'instabilité${\underline {)\;}}$des équilibres d'un P.P.S. : nous avons vu que la force motrice au voisinage d’un équilibre stable devait être « de rappel » $\;{\big [}$ainsi au voisinage de «$\;\theta _{\text{éq}}=0\;$», «$\;F(\theta _{\text{éq}}+\varepsilon )=-m\;g\;\sin(\varepsilon )\simeq -m\;g\;\varepsilon \;$» force de rappel caractérisant un équilibre stable alors qu'au voisinage de «$\;\theta _{\text{éq}}=\pi \;$», «$\;F(\theta _{\text{éq}}+\varepsilon )=-m\;g\;\sin(\pi +\varepsilon )=m\;g\;\sin(\varepsilon )\simeq$ $m\;g\;\varepsilon \;$» force répulsive caractérisant un équilibre instable${\big ]}$, nous en déduisons la « même propriété pour le moment scalaire moteur » :

            Retour sur la détermination de la stabilité$\color {transparent}{\;(}$ou de l'instabilité$\color {transparent}{)\;}$des équilibres d'un P.P.S. : si, au voisinage d’un équilibre, le « moment scalaire moteur » est « de rappel », l’équilibre est stable,
        Retour sur la détermination de la stabilité$\color {transparent}{\;(}$ou de l'instabilité$\color {transparent}{)\;}$des équilibres d'un P.P.S. : si, au voisinage d'un équilibre le « moment scalaire moteur » s’il est « répulsif », l’équilibre est instable
            Retour sur la détermination de la stabilité$\color {transparent}{\;(}$ou de l'instabilité$\color {transparent}{)\;}$des équilibres d'un P.P.S. : ${\big [}$ainsi au voisinage de «$\;\theta _{\text{éq}}=0\;$», «$\;{\mathcal {M}}_{\!\Delta _{O},\,m\,{\vec {g}}}(\theta _{\text{éq}}+\varepsilon )=-m\;g\;{\mathit {l}}\;\sin(\varepsilon )\simeq -m\;g\;{\mathit {l}}\;\varepsilon \;$» moment scalaire de rappel caractérisant un équilibre stable alors qu'au voisinage de «$\;\theta _{\text{éq}}=\pi \;$», «$\;{\mathcal {M}}_{\!\Delta _{O},\,m\,{\vec {g}}}(\theta _{\text{éq}}+\varepsilon )=-m\;g\;{\mathit {l}}\;\sin(\pi +\varepsilon )=m\;g\;{\mathit {l}}\;\sin(\varepsilon )\simeq m\;g\;{\mathit {l}}\;\varepsilon \;$» moment scalaire répulsif caractérisant un équilibre instable${\big ]}$ ;
            Retour sur la détermination de la stabilité$\color {transparent}{\;(}$ou de l'instabilité$\color {transparent}{)\;}$des équilibres d'un P.P.S. : on pourrait aussi développer une méthode graphique de vérification de la stabilité $\;{\big (}$ou de l'instabilité${\big )}\;$ des équilibres du P.P.S. identique à celle développée au paragraphe « méthode graphique de vérification de la stabilité ou de l'instabilité des équilibres du P.P.S. à un degré de liberté » du chap.$18$ de la leçon « Mécanique 1 (PCSI) » en étudiant graphiquement le « moment scalaire moteur » à la place de la « composante de force motrice ».

En complément : généralisation à la détermination des positions d’équilibre d’un solide en rotation autour d’un axe fixe ainsi que de leur stabilité ou instabilité en termes de moment scalaire moteur

Détermination des positions d'équilibre d'un solide en rotation autour d’un axe fixe :

     Il y a deux types de moments scalaires agissant sur un solide en rotation :

• ceux des forces « motrices » qui sont les causes de modification du moment cinétique scalaire $\;{\big [}$correspondant à des actions ou des réactions tangentielles au mouvement${\big ]}$, ces moments scalaires étant qualifiés de « moteurs » et
• ceux des forces « non motrices » qui sont $\;\perp \;$ au mouvement $\;{\big [}$correspondant aussi bien à des actions qu'à des réactions pourvues qu'elles soient $\;\perp \;$ au mouvement${\big ]}$, les moments scalaires de ces forces étant en fait nuls ;

     soit «$\;{\mathcal {M}}_{\!\Delta _{O}}(\theta )\;$» le « moment scalaire moteur agissant sur le solide en rotation autour de l'axe $\;\Delta _{O}\;$ et ne s’annulant pas avec le mouvement », les abscisses angulaires «$\;\theta _{\text{éq}}\;$» des positions d’équilibre du solide sont les zéros de «$\;{\mathcal {M}}_{\!\Delta _{O}}(\theta )\;$» à savoir les valeurs «$\;\theta _{\text{éq}}\;$ telles que $\;{\mathcal {M}}_{\!\Delta _{O}}(\theta _{\text{éq}})=0\;$».

Détermination de la stabilité${\underline {\;(}}$ou de l'instabilité${\underline {)\;}}$des équilibres du solide précédent en rotation autour d’un axe fixe :

     pour étudier la stabilité $\;{\big (}$ou l'instabilité${\big )}\;$ de l’équilibre repéré par «$\;\theta _{\text{éq}}\;$ telle que $\;{\mathcal {M}}_{\!\Delta _{O}}(\theta _{\text{éq}})=0\;$», faire un D.L. à l’ordre le plus bas non nul du « moment scalaire moteur $\;{\mathcal {M}}_{\!\Delta _{O}}(\theta )\;$» au voisinage de la position d’équilibre «$\;\theta _{\text{éq}}\;$» et conclure selon les résultats suivants :

• cas usuel «$\;{\dfrac {d{\mathcal {M}}_{\!\Delta _{O}}}{d\theta }}(\theta _{\text{éq}})\neq 0\;$» : le développement de $\;{\mathcal {M}}_{\!\Delta _{O}}(\theta )\;$ au voisinage de $\;\theta _{\text{éq}}\;$ est limité à l'ordre un «$\;{\mathcal {M}}_{\!\Delta _{O}}(\theta _{\text{éq}}+\varepsilon )\simeq {\dfrac {d{\mathcal {M}}_{\!\Delta _{O}}}{d\theta }}(\theta _{\text{éq}})\;\varepsilon \;$»,
                                        cas usuel : si «$\;{\dfrac {d{\mathcal {M}}_{\!\Delta _{O}}}{d\theta }}(\theta _{\text{éq}})\;$ est $\;<0\;$», $\;{\mathcal {M}}_{\!\Delta _{O}}(\theta )\;$ est « un moment scalaire de rappel » et l'équilibre est « stable »,
                                        cas usuel : si «$\;{\dfrac {d{\mathcal {M}}_{\!\Delta _{O}}}{d\theta }}(\theta _{\text{éq}})\;$ est $\;>0\;$», $\;{\mathcal {M}}_{\!\Delta _{O}}(\theta )\;$ est « un moment scalaire répulsif » et l'équilibre est « instable »,
• cas peu fréquent «$\;{\dfrac {d{\mathcal {M}}_{\!\Delta _{O}}}{d\theta }}(\theta _{\text{éq}})=0\;$» : le développement de $\;{\mathcal {M}}_{\!\Delta _{O}}(\theta )\;$ au voisinage de $\;\theta _{\text{éq}}\;$ est limité à l'ordre deux ou plus :
                                        cas peu fréquent : $\succ \;$ si «$\;{\dfrac {d^{2}{\mathcal {M}}_{\!\Delta _{O}}}{d\theta ^{2}}}(\theta _{\text{éq}})\;$ est $\;\neq 0\;$», le développement de $\;{\mathcal {M}}_{\!\Delta _{O}}(\theta )\;$ au voisinage de $\;\theta _{\text{éq}}\;$ est limité à l'ordre deux selon «$\;{\mathcal {M}}_{\!\Delta _{O}}(\theta _{\text{éq}}+\varepsilon )\simeq {\dfrac {d^{2}{\mathcal {M}}_{\!\Delta _{O}}}{d\theta ^{2}}}(\theta _{\text{éq}})\;{\dfrac {\varepsilon ^{2}}{2}}\;$» et «$\;{\mathcal {M}}_{\!\Delta _{O}}(\theta )\;$ est toujours du signe de $\;{\dfrac {d^{2}{\mathcal {M}}_{\!\Delta _{O}}}{d\theta ^{2}}}(\theta _{\text{éq}})\;$ quel que soit le signe de $\;\varepsilon \;$» correspondant à un équilibre stable d'un côté et instable de l'autre donc « globalement instable »,
                                        cas peu fréquent : $\succ \;$ si «$\;{\dfrac {d^{2}{\mathcal {M}}_{\!\Delta _{O}}}{d\theta ^{2}}}(\theta _{\text{éq}})\;$ est $\;=0\;$ mais $\;{\dfrac {d^{3}{\mathcal {M}}_{\!\Delta _{O}}}{d\theta ^{3}}}(\theta _{\text{éq}})\;\neq 0\;$», le développement de $\;{\mathcal {M}}_{\!\Delta _{O}}(\theta )\;$ au voisinage de $\;\theta _{\text{éq}}\;$ est limité à l'ordre trois «$\;{\mathcal {M}}_{\!\Delta _{O}}(\theta _{\text{éq}}+\varepsilon )$ $\simeq {\dfrac {d^{3}{\mathcal {M}}_{\!\Delta _{O}}}{d\theta ^{3}}}(\theta _{\text{éq}})\;{\dfrac {\varepsilon ^{3}}{6}}\;$»,
                                                                                                                                                cas peu fréquent : $\blacktriangleright \;$ si «$\;{\dfrac {d^{3}{\mathcal {M}}_{\!\Delta _{O}}}{d\theta ^{3}}}(\theta _{\text{éq}})\;$ est $\;<0\;$», $\;{\mathcal {M}}_{\!\Delta _{O}}(\theta )\;$ est « un moment scalaire de rappel » et l'équilibre est « stable »,
                                                                                                                                                cas peu fréquent : $\blacktriangleright \;$ si «$\;{\dfrac {d^{3}{\mathcal {M}}_{\!\Delta _{O}}}{d\theta ^{3}}}(\theta _{\text{éq}})\;$ est $\;>0\;$», $\;{\mathcal {M}}_{\!\Delta _{O}}(\theta )\;$ est « un moment scalaire répulsif » et l'équilibre est « instable »,
• cas inexistant en pratique «$\;{\dfrac {d{\mathcal {M}}_{\!\Delta _{O}}}{d\theta }}(\theta _{\text{éq}})=0$, $\;{\dfrac {d^{2}{\mathcal {M}}_{\!\Delta _{O}}}{d\theta ^{2}}}(\theta _{\text{éq}})=0\;$ et $\;{\dfrac {d^{3}{\mathcal {M}}_{\!\Delta _{O}}}{d\theta ^{3}}}(\theta _{\text{éq}})=0\;$» : le développement de $\;{\mathcal {M}}_{\!\Delta _{O}}(\theta )\;$ au voisinage de $\;\theta _{\text{éq}}\;$ est limité à l'ordre quatre ou plus :
                                                                                                                           cas inexistant en pratique : $\succ \;$ si «$\;{\dfrac {d^{4}{\mathcal {M}}_{\!\Delta _{O}}}{d\theta ^{4}}}(\theta _{\text{éq}})\;$ est $\;\neq 0\;$» le développement de $\;{\mathcal {M}}_{\!\Delta _{O}}(\theta )\;$ au voisinage de $\;\theta _{\text{éq}}\;$ est limité à l'ordre quatre selon «$\;{\mathcal {M}}_{\!\Delta _{O}}(\theta _{\text{éq}}+\varepsilon )\simeq {\dfrac {d^{4}{\mathcal {M}}_{\!\Delta _{O}}}{d\theta ^{4}}}(\theta _{\text{éq}})\;{\dfrac {\varepsilon ^{4}}{24}}\;$» et «$\;{\mathcal {M}}_{\!\Delta _{O}}(\theta )\;$ est toujours du signe de $\;{\dfrac {d^{4}{\mathcal {M}}_{\!\Delta _{O}}}{d\theta ^{4}}}(\theta _{\text{éq}})\;$ quel que soit le signe de $\;\varepsilon \;$» correspondant à un équilibre stable d'un côté et instable de l'autre donc « globalement instable »,
                                                                                                                           cas inexistant en pratique : $\succ \;$ si «$\;{\dfrac {d^{4}{\mathcal {M}}_{\!\Delta _{O}}}{d\theta ^{4}}}(\theta _{\text{éq}})\;$ est $\;=0\;$ mais $\;{\dfrac {d^{5}{\mathcal {M}}_{\!\Delta _{O}}}{d\theta ^{5}}}(\theta _{\text{éq}})\neq 0\;$», le développement de $\;{\mathcal {M}}_{\!\Delta _{O}}(\theta )\;$ au voisinage de $\;\theta _{\text{éq}}\;$ est limité à l'ordre cinq selon «$\;{\mathcal {M}}_{\!\Delta _{O}}(\theta _{\text{éq}}+\varepsilon )\simeq {\dfrac {d^{5}{\mathcal {M}}_{\!\Delta _{O}}}{d\theta ^{5}}}(\theta _{\text{éq}})\;{\dfrac {\varepsilon ^{5}}{120}}\;$», correspondant à un équilibre « stable pour $\;{\dfrac {d^{5}{\mathcal {M}}_{\!\Delta _{O}}}{d\theta ^{5}}}(\theta _{\text{éq}})\;<\;0\;$» et « instable pour $\;{\dfrac {d^{5}{\mathcal {M}}_{\!\Delta _{O}}}{d\theta ^{5}}}(\theta _{\text{éq}})\;>\;0\;$».

Rappel du cas particulier : pendule pesant simple (non amorti à un degré de liberté) utilisant un fil idéal, détermination de la tension du fil et conditions de lancement pour que le fil reste tendu

Schéma d'un P.P.S.N.A. à un degré de liberté lancé dans les C.I. $\;1{\mathfrak {a}}\cup 1{\mathfrak {b}}\;$, le point $\;M\;$ du P.P.S.N.A. à fil idéal supposé tendu ayant un mouvement circulaire d'axe $\;\Delta \;$ passant par $\;O\;$ avec repérage polaire de pôle $\;O$ $\;{\big (}$et d'axe $\;\Delta {\big )}\;$ de $\;M\;$ et représentation des deux forces s'appliquant sur lui

     Voir le paragraphe « 2^ème additif : “dans le cas où le P.P.S. est constitué d'un fil idéal se substituant à la tige rigide, valider la condition de tension du fil” » du chap.$17$ de la leçon « Mécanique 1 (PCSI) », ci-dessous nous rappelons les principaux résultats :

     Après utilisation successive de la projection sur $\;{\vec {u}}_{r}\;$ de la r.f.d.n. appliquée à $\;M\;$ $\Rightarrow$ «$\;{\overline {T}}(t)={\vec {T}}(t)\cdot {\vec {u}}_{r}=-m\,\left\lbrace {\mathit {l}}\;{\dot {\theta }}^{2}\!(t)+g\;\cos \!\left[\theta (t)\right]\right\rbrace \;$» et de l'intégrale 1^ère énergétique de $\;M\;$ «$\;{\dfrac {1}{2}}\;m\;{\mathit {l}}^{\,2}\;{\dot {\theta }}^{2}\!(t)+m\;g\;{\mathit {l}}\,\left\lbrace 1-\cos \!\left[\theta (t)\right]\right\rbrace =E_{m,\,0}\;$», on trouve, pour composante du vecteur tension du fil $\;{\vec {T}}(t)\;$ sur $\;{\vec {u}}_{r}$,

«$\;{\overline {T}}(t)={\vec {T}}(t)\cdot {\vec {u}}_{r}=-m\;g\,\left\lbrace {\dfrac {2\;E_{m,\,0}}{m\;g\;{\mathit {l}}}}-2+3\;\cos \!\left[\theta (t)\right]\right\rbrace \;$» ;

     le fil restant tendu dans tout le mouvement si $\;{\overline {T}}(\theta )\;$ est $\;<0\;\;\forall \;\theta$, ce qui est réalisé « si le maximum de $\;{\overline {T}}(\theta )\;$ est $\;<0\;$» il convient, pour poursuivre, d'introduire le domaine de variation de $\;\theta$, ce qui nécessite de distinguer la nature révolutive ou oscillatoire hypothétique du P.P.S.N.A. suivant son énergie mécanique initiale :

• si «$\;E_{m,\,0}\;$ est $\;>\;$ à $\;2\;m\;g\;{\mathit {l}}\;$», le mouvement du P.P.S.N.A., dans l'hypothèse où le fil resterait toujours tendu, étant révolutif, le domaine de variation de $\;\theta \;$ est «$\;\left[\theta _{0}\,,\,+\infty \right[\;$ pour $\;{\dot {\theta }}_{0}>0\;$» et «$\;\left]-\infty \,,\,\theta _{0}\right]\;$ pour $\;{\dot {\theta }}_{0}<0\;$» mais la fonction $\;{\overline {T}}(\theta )=-m\;g\,\left[{\dfrac {2\;E_{m,\,0}}{m\;g\;{\mathit {l}}}}-2+3\;\cos(\theta )\right]\;$ étant $\;2\;\pi$-périodique et paire, « la recherche de son maximum peut être restreinte à l'intervalle $\;\left[0\,,\,+\pi \right]\;$ quel que soit le signe de $\;{\dot {\theta }}_{0}\;$» c'est-à-dire une même condition indépendante du signe de $\;{\dot {\theta }}_{0}$, «$\;\max \limits _{\left[0\,,\,+\pi \right]}\left\lbrace {\overline {T}}(\theta )\right\rbrace <0\;$» ;      $\;{\overline {T}}(\theta )=-m\;g\,\left[{\dfrac {2\;E_{m,\,0}}{m\;g\;{\mathit {l}}}}-2+3\;\cos(\theta )\right]\;$ étant une fonction $\;\nearrow \;$ sur $\;\left[0\,,\,+\pi \right]$, la condition se réécrit «$\;\max \limits _{\left[0\,,\,+\pi \right]}\left\lbrace {\overline {T}}(\theta )\right\rbrace ={\overline {T}}(+\pi )<0\;$» soit finalement « la condition pour que le mouvement du P.P.S.N.A. à fil idéal soit effectivement révolutif sans que le fil ne se détende est $\;E_{m,\,0}>{\dfrac {5}{2}}\;m\;g\;{\mathit {l}}\;$» ;
• si «$\;E_{m,\,0}\;$ est $\;<\;$ à $\;2\;m\;g\;{\mathit {l}}\;$», le mouvement du P.P.S.N.A., dans l'hypothèse où le fil resterait toujours tendu, étant oscillatoire, le domaine de variation de $\;\theta \;$ est «$\;\left[-\theta _{m}\,,\,+\theta _{m}\right[\;$ dans lequel l'amplitude $\;\theta _{m}=$ $\arccos \!\left[1-{\dfrac {E_{m,\,0}}{m\;g\;{\mathit {l}}}}\right]\;$» mais la fonction $\;{\overline {T}}(\theta )=-m\;g\,\left[{\dfrac {2\;E_{m,\,0}}{m\;g\;{\mathit {l}}}}-2+3\;\cos(\theta )\right]\;$ étant $\;2\;\pi$-périodique et paire, « la recherche de son maximum peut être restreinte à un intervalle à partir duquel on obtient toutes les valeurs possibles de $\;{\overline {T}}(\theta )$, à savoir $\;\left[0\,,\,\theta _{m}\right]\;$», la condition de fil tendu pour un mouvement hypothétique oscillatoire se réécrivant «$\;\max \limits _{\left[0\,,\,\theta _{m}\right]}\left\lbrace {\overline {T}}(\theta )\right\rbrace <0\;$» ;      $\;{\overline {T}}(\theta )=-m\;g\,\left[{\dfrac {2\;E_{m,\,0}}{m\;g\;l}}-2+3\;\cos(\theta )\right]\;$ étant une fonction $\;\nearrow \;$ sur $\;\left[0\,,\,\theta _{m}\right]$, la condition se réécrit «$\;\max \limits _{\left[0\,,\,\theta _{m}\right]}\left\lbrace {\overline {T}}(\theta )\right\rbrace ={\overline {T}}(\theta _{m})<0\;$» soit finalement « la condition pour que le mouvement du P.P.S.N.A. à fil idéal soit effectivement oscillatoire sans que le fil ne se détende est $\;E_{m,\,0}<m\;g\;{\mathit {l}}\;$» ;
• finalement si «$\;E_{m,\,0}\in \left[m\;g\;{\mathit {l}}\,,\,{\dfrac {5}{2}}\;m\;g\;{\mathit {l}}\right[\;$», le fil se détend pour «$\;\theta _{\text{détente}}\;$ telle que $\;{\overline {T}}(\theta _{\text{détente}})=0\;$» et on obtient «$\;\vert \theta _{\text{détente}}\vert =\arccos \!\left[{\dfrac {2}{3}}-{\dfrac {2\;E_{m,\,0}}{3\;m\;g\;{\mathit {l}}}}\right]\,\in \left[{\dfrac {\pi }{2}}\,,\,\pi \right]\;$».