Mécanique pour l'enseignement technique industriel/Modélisation - Les actions mécaniques

Début de la boite de navigation du chapitre

Modélisation - Les actions mécaniques

Chapitre no11
Leçon : Mécanique pour l'enseignement technique industriel
Chap. préc. :	Mouvement plan
Chap. suiv. :	Statique - Principe fondamental de la statique

   

fin de la boite de navigation du chapitre

En raison de limitations techniques, la typographie souhaitable du titre, « Mécanique pour l'enseignement technique industriel : Modélisation - Les actions mécaniques
Mécanique pour l'enseignement technique industriel/Modélisation - Les actions mécaniques », n'a pu être restituée correctement ci-dessus.

Présentation

Le but de ce chapitre est d'expliquer comment on modélise les actions mécaniques. Cela permet de déterminer les efforts que doivent supporter les structures, et que doivent développer les actionneurs (vérins, moteurs), et donc de vérifier des systèmes existants ou de dimensionner des projets.

Pour pouvoir effectuer des calculs, il faut quantifier ces actions, c'est-à-dire les exprimer sous forme de nombres.

Objectif

Le but de ce chapitre est de savoir donner les caractéristiques une action mécanique : point d'application, direction, sens, intensité.

Savoirs techniques

Connaissances (notions, concepts)	Niveau
	1	2	3	4
Actions mécaniques sur un solide : modélisation des actions mécaniques : forces, moments, couples, systèmes équivalents, actions de contact : action de liaison entre solides, actions dues aux fluides, actions à distance			×
Actions mécaniques dans les liaisons : actions associées aux liaisons mécaniques élémentaires		×
Principe des actions mutuelles : expression vectorielle.			×

Actions mécaniques

Début d'une définition

Action mécanique

Phénomène pouvant modifier le mouvement d'un objet ou pouvant le déformer.

Fin de la définition

Activité 1

Donnez des exemples d'actions mécaniques.

Solution

Voici quelques exemples d'actions mécaniques :

• le poids provoque la chute d'un objet ; il fait fléchir une tige ou lame fine et longue, étire un ressort ;
• le vent et le courant de l'eau font avancer un navire, tourner un moulin, une turbine ; il font se courber un roseau ;
• une pièce peut pousser ou tirer une autre pour la mettre en mouvement : vérin, câble, chaîne, barre de traction, …
• un aimant attire une pièce d'acier ;
• une manivelle, un volant mettent un système en rotation ;
• un tournevis fait tourner une vis ;
• …

Activité 2

Classer les actions mécaniques en familles.

Solution

On peut distinguer les actions selon la distance entre la source d'effort et l'effet :

• actions de contact : poussée ou traction directes, d'un solide ou d'un fluide ;
• actions à distance : poids, magnétisme.

On peut aussi les distinguer selon la nature du mouvement ou de la déformation créées :

• mouvement ou déformation linéaire (en ligne droite) ;
• mouvement ou déformation en tournant.

Effet des actions mécaniques

Début d'une définition

Force et moment

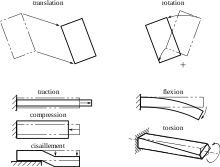
On distingue principalement deux types d'actions mécaniques :

• les forces, qui peuvent créer un mouvement ou une déformation linéaires ;
• les moments ou couples, qui peuvent créer un mouvement ou une déformation en tournant.

Fin de la définition

Les actions mécaniques et leurs effets

	Force	Moment, couple
Mouvement	Translation rectiligne	Rotation
Déformation	Élongation, compression, cisaillement	Torsion, flexion

Forces

Une force est donc un phénomène pouvant créer un mouvement de translation, étirer une pièce, l'écraser ou la cisailler. Alors que certaines grandeurs peuvent se représenter par un simple nombre — température, pression, masse —, ce n'est pas le cas d'une force : si l'on pousse une table « comme ci » ou « comme ça », on n'obtient pas le même effet (le même déplacement). Pour la représenter, il faut donc utiliser un objet mathématique qui décrive la direction et le sens : un vecteur.

Dynamomètre à ressort hélicoïdal

Un vecteur force $\vec \mathrm{F}$ est donc caractérisé par :

• son point d'application : là où le phénomène agit ;
• la direction : direction de la translation, de la déformation ;
• le sens : sens de la translation, de la déformation ;
• l'intensité, exprimée en newtons (abréviation N) ; on parle aussi de « norme du vecteur », notée $\| \vec \mathrm{F} \|$.

L'intensité d'une force se mesure par la déformation d'un ressort ; l'appareil s'appelle un dynamomètre.

Pour l'intensité, on utilise aussi le décanewton (daN) :

1 daN = 10 N

1 N = 1 daN

ce qui correspond grosso modo à une ancienne unité, le kilogramme-force (kgf).

On synthétise ces caractéristiques dans un tableau.

Caractéristiques des actions mécaniques

Action	Point d'application	Direction	Sens	Intensité
…	…	…	…	… (N)

Il peut y avoir une ambiguïté entre direction et sens :

• direction : c'est une droite géométrique, soit désignée par deux point, par exemple « (AB) », soit par l'angle avec l'horizontale ou la verticale, par exemple « ∠ 45° », soit un trait horizontal « — » ou vertical « | » ;
• sens : c'est une flèche ayant la même orientation que la direction, du type « → », « ↗ », « ↑ », …

Par analogie, pour signaler un accident sur une autoroute, il faut indiquer entre autres :

• le nom de l'autoroute (par exemple « A1 ») : c'est la direction ;
• le sens de circulation de la voie (par exemple « dans le sens Paris vers Lille ») : c'est le sens.

Sur le dessin, le vecteur est représenté par une flèche ayant la direction et le sens de l'action mécanique. Elle touche le point d'application, par le pied ou par la pointe. La longueur est déterminée par une échelle, par exemple

« 1 mm représente 1 N » : une force de 25 N est représentée par une flèche de 25 mm (2,5 cm) de long ;

parfois, aucune échelle n'est indiquée, on choisit librement, « arbitrairement », la longueur de la flèche.

Poids

Définition et caractéristiques

Le poids est une force qui attire les objets vers le bas ; c'est une action qu'exerce la Terre sur les objets. C'est donc une action à distance : elle s'exerce même si l'on est à l'étage d'un bâtiment ou dans un avion, le contact avec le sol n'est pas nécessaire.

Il faut bien distinguer les notions de masse et de poids.

Masse et poids

Masse	Poids
La masse représente la quantité de matière ; elle est la même partout. La matière est composée d'atomes, les atomes comportent un noyau composé de particules appelées nucléons (protons et neutrons) ; la masse représente le nombre de nucléons.	Le poids varie selon l'endroit où l'on se trouve. Sur la Lune, il est 6 fois moins important que sur Terre. Sur Terre, il est légèrement plus important aux pôles qu'à l'équateur.
La masse représente l'inertie, c'est-à-dire la difficulté que l'on a à mettre un objet en mouvement. On peut pousser une voiture, il est plus facile de pousser une Fiat 500 qu'un Porsche Cayenne.	Le poids le phénomène qui tire l'objet vers le bas. Personne n'est capable de lever une voiture…
La masse se mesure avec une balance	Le poids se mesure avec un dynamomètre, ou peson
La masse se représente par un nombre ; l'unité est le kilogramme (kg)	Le poids se représente par un vecteur ; l'unité est le newton (N)

• 

  Balance de Roberval

• 

  Balance romaine

• 

  Balance électronique

• 

  Pesons (dynamomètres)

• 

  Principe du dynamomètre

La confusion vient du fait que le poids est proportionnel à la masse : sur Terre, on a

Début d'une définition

Poids

P = mg

Fin de la définition

avec

• P : intensité du poids (N) ; $\mathrm{P} = \| \vec \mathrm{P} \|$ ;
• m : masse (kg) ;
• g : gravité (pesanteur), g ≃ 9,81 N/kg ;
  on prend souvent pour simplifier g ≃ 10 N/kg.

L'unité de g est également notée m/s² (mètre par seconde au carré) ; en effet, c'est aussi l'accélération d'un objet tombant en chute libre (en négligeant le frottement de l'air), g est d'ailleurs appelé « accélération de la gravité ».

g ≃ 9,81 m/s² ≃ 10 m/s².

Le poids est une force répartie : chaque élément d'un objet a son propre poids. Par exemple, pour un humain, chaque organe — doigt, oreille, nez, …— a son propre poids. On modélise le poids comme une force s'appliquant en un point appelé « centre de gravité » et noté G.

Début d'une définition

Centre de gravité G

Point d'application du poids d'un objet

Fin de la définition

Une chute est un mouvement vertical dirigé vers le bas ; le poids est donc une force verticale dirigée vers le bas.

On a ainsi toutes les caractéristiques du poids ; elles sont résumées dans le tableau ci-dessous.

Caractéristiques du poids

Action	Point d'application	Direction	Sens	Intensité
$\vec \mathrm{P}$	G	|	↓	mg

Calcul du poids d'une pièce

Considérons une pièce faite d'un seul matériau. Son poids P dépend de la masse m ; cette masse dépend de la quantité de matière, c'est-à-dire

• du volume de la pièce V, exprimé en m³ ;
• du matériau, et plus précisément de sa masse volumique ρ, exprimée en kg/m³.

Au lieu de la masse volumique, on utilise parfois la densité par rapport à l'eau d, qui est donnée sans unité mais correspond à la masse volumique exprimée en kg/dm³ (ou kg/L) ; dans ce cas-là, on exprime le volume en dm³.

On a ainsi :

• m = ρ×V
• P = m×g.

Il faut donc d'abord calculer le volume de la pièce.

Exemples

Calculer le poids d'une planche de bois de densité d = 0,5 et de dimensions 2 m×14 cm ép. 21 mm. On prendra g = 9,81 N/kg.

• 

  Planche

• 

  Dimensions

Solution

Convertissons toutes les longueurs en dm :

Conversion

m	dm	cm	mm
2	0
	1,	4
	0,	2	1

On a donc

V = L×ℓ×e = 20×1,4×0,21 = 5,88 dm³

m = ρV = 0,5×5,88 = 2,94 kg

P = mg = 2,94×9,81 = 28,8 N

 

Calculer le poids d'un barreau cylindrique (rond) de diamètre ∅10 mm et de 200 mm de long, en acier de masse volumique ρ = 7 800 kg/m³. On prendra g = 10 N/kg.

• 

  Barres cylindriques (« ronds »)

• 

  Dimensions

Solution

Convertissons toutes les longueurs en m :

Conversion

m	dm	cm	mm
0,	0	1	0
0,	2	0	0

On a donc

V = π×r²×h = π×0,005²×0,2 = 1,57⋅10^-5 m³ = 0,000 015 7 m³

m = ρV = 7 800×1,57⋅10^-5 = 0,123 kg

P = mg = 0,123×10 = 1,23 N

 

Voir les exercices sur : Poids et centre de gravité > Élévateur à bande.

Détermination du centre de gravité

Le centre de gravité G est le point d'application du poids d'un objet. Il faut donc le connaître pour pouvoir résoudre les problèmes de statique.

Caisse sur un plan incliné : lorsque la verticale au centre de gravité sort de la zone d'appui, la caisse bascule

Élingage d'un ballon de reflux : le point d'accrochage A doit être à l'aplomb du centre de gravité G

Mais la connaissance du centre de gravité est aussi un élément de sécurité important, concernant la stabilité des objets :

• lorsque l'on pose un objet sur des appuis, il faut impérativement que le centre de gravité se trouve entre les appuis, sinon l'objet bascule ; c'est notamment critique dans le cas d'un plan incliné ;
• lorsque l'on lève un objet avec une élingue (câble, sangle), le centre de gravité se met à l'aplomb du point d'accroche de l'élingue ; si les deux ne sont pas alignés au départ, l'objet va basculer.

L'élingage est d'ailleurs une manière de déterminer la position du centre de gravité : on lève l'objet de quelques centimètres, et s'il bascule, on le repose et on décale le point d'accrochage, jusqu'à obtenir l'équilibre.

Voir les exercices sur : Poids et centre de gravité > Étude d'un tube de cuivre.

Pour déterminer la position du centre de gravité, on applique les règles suivantes.

Début d'un principe

1^er principe

Si l'objet est fait d'un matériau homogène et qu'il présente un plan de symétrie orthogonale (miroir), G est dans ce plan de symétrie.
S'il présente un axe de symétrie orthogonale, G est sur cet axe. S'il présente un point de symétrie centrale, G est ce point.

Fin du principe

Pour les objets de forme simple — cube, parallélépipède rectangle (et notamment tôles rectangulaires, plats — barres de section rectangulaire — et carrés — barres de section carrée), sphères (boules, réservoirs sphériques), cylindres (et notamment disques, ronds — barres de section circulaire —, tubes et viroles) —, le centre de gravité est le centre de l'objet.

• 

  Cylindre

• 

  Parallélépipède rectangle

Triangle rectangle

Début d'un principe

2^e principe

Dans le cas d'un prisme dont la base est un triangle rectangle, le centre de gravité se situe sur la droite située au tiers des côtés de l'angle droit.

Fin du principe

Centre de gravité d'un système formé de deux sphères

Début d'un principe

3^e principe

Si le système est composé de deux objets rep. 1 et 2, de masse respective P₁ et P₂, et de centre de gravités respectifs G₁ et G₂ situés à l'abscisse x₁ et x₂, alors le centre de gravité total G est situé à l'abscisse

$x_\mathrm{G} = \frac{\mathrm{P}_1 x_1 + \mathrm{P}_2 x_2}{\mathrm{P}_1 + \mathrm{P}_2}$.

C'est la moyenne pondérée des abscisses.

Fin du principe

Cette méthode peut s'étendre à n pièces de masse P₁, P₂, …, P_n et dont les abscisses des centres de gravité sont notées x₁, x₂, …, x_n :

$x_\mathrm{G} = \frac{\mathrm{P}_1 x_1 + \mathrm{P}_2 x_2 + \dots + \mathrm{P}_n x_n}{\mathrm{P}_1 + \mathrm{P}_2 + \dots + \mathrm{P}_n} = \frac{\sum_{i=1}^n \mathrm{P}_i x_i}{\sum_{i=1}^n \mathrm{P}_i} = \frac{\sum_{i=1}^n \mathrm{P}_i x_i}{\mathrm{P_{total}}}$.

On peut présenter le calcul sous la forme d'un tableau.

Calcul du centre de gravité

Pièce i	Pi	xi	Pixi
1	P1	x1	P1x1
2	P2	x2	P2x2
…
n	Pn	xn	Pnxn
Somme	Ptotal	—	A

et

$x_\mathrm{G} = \frac{\mathrm{A}}{\mathrm{P_{total}}}$.

Exemple

La pièce 1 a pour masse P₁ = 100 N et son centre de gravité G₁ a pour abscisse x₁ = 1 m ; pour la pièce 2, on a P₂ = 50 N et x₂ = 3 m.

Calcul du centre de gravité

Pièce i	Pi	xi	Pixi
1	100	1	100
2	50	3	150
Somme	150	—	250

donc

$x_\mathrm{G} = \frac{250}{150} = 1,67\ \mathrm{m}$.

On peut aussi présenter le calcul sous la forme d'une formule :

$x_\mathrm{G} = \frac{\sum_{i=1}^2 \mathrm{P}_i x_i}{\sum_{i=1}^2 \mathrm{P}_i} = \frac{\mathrm{P}_1 x_1 + m_2 x_2}{\mathrm{P}_1 + m_2} = \frac{100 \times 1 + 50 \times 3}{100 + 50} = 1,67\ \mathrm{m}$.

Note

On peut utiliser n'importe quelle unité de longueur tant que l'on utilise toujours la même ; pour les grands systèmes, il est souvent intéressant d'utiliser des mètres afin de manipuler des nombres plus petits. Par ailleurs, la position de l'origine des abscisses O n'a pas d'importance. Il arrive fréquemment que l'on prenne un des centres de gravité comme origine, par exemple O = G₁ et donc x₁ = 0, ce qui simplifie les calculs.

Note

Puisque le poids est proportionnel à la masse, on peut utiliser la masse (en kg) pour pondérer :

$x_\mathrm{G} = \frac{p_1 x_1 + p_2 x_2 + \dots + p_n x_n}{p_1 + p_2 + \dots + p_n} = \frac{\sum_{i=1}^n m_i x_i}{\sum_{i=1}^n m_i}$.

Si les pièces sont en tôles qui sont faites du même matériau et qui ont la même épaisseur, on peut utiliser l'aire des pièces (en m², cm² ou mm²), puisque la masse est proportionnelle à l'aire :

$x_\mathrm{G} = \frac{\mathrm{S}_1 x_1 + \mathrm{S}_2 x_2 + \dots + \mathrm{S}_n x_n}{\mathrm{S}_1 + \mathrm{S}_2 + \dots + \mathrm{S}_n} = \frac{\sum_{i=1}^n \mathrm{S}_i x_i}{\sum_{i=1}^n \mathrm{S}_i}$.

Voir les exercices sur : Poids et centre de gravité > Support d'un filtre à vin.

Forces de pression

La pression est une force répartie sur une surface

Début d'une définition

Définition

Une pression est une force qui se répartit sur une surface :

$\mathrm{P} = \frac{\mathrm{F}}{\mathrm{S}}$

où

• P est la pression ; l'unité internationale est le pascal (Pa) ;
• F est la force, en newton (N) ;
• S est l'aire de la surface, en mètres carrés (m²) ;

on a donc 1 Pa = 1 N/m².

Fin de la définition

La pression peut être l'action d'un fluide — gaz (pression atmosphérique, circuit pneumatique), liquide (pression de l'eau, circuit hydraulique) — ou bien d'un solide (pression de contact).

Une pression de 1 Pa est très faible ; c'est le poids de 100 g réparti sur un carré de 1 m de côté. Dans la pratique, on utilise

• le bar (bar) :
  • 1 bar = 100 000 Pa = 10⁵ Pa,
  • 1 bar = 1 daN/cm² ;
• le mégapascal (MPa) :
  • 1 MPa = 1 000 000 Pa = 10⁶ Pa,
  • 1 MPa = 1 N/mm²,
  • 1 MPa = 10 bar.

La pression atmosphérique vaut à peu près 1 bar ; la valeur de référence est 1 013 bar (mais la valeur réelle dépend du lieu et du moment). En météorologie, on l'exprime en milliers d'hectopascals (hPa) :

1 hPa = 100 Pa

1 000 hPa = 100 000 Pa

Début de l'exemple

Exemple

Si j'appuie avec mon doigt sur une table, il ne se passe rien de particulier : la force, de l'ordre de 500 N, est répartie sur la surface de contact de mon doigt, de l'ordre de 50 mm², soit une pression

P = F/S = 500/50 = 10 MPa.

Si maintenant j'appuie sur une punaise, la force est concentrée sur la pointe don l'aire est environ 0,05 mm² ; la pression vaut alors

P = F/S = 500/0,05 = 10 000 MPa ;

la punaise perce le bois de la table.

Fin de l'exemple

La force résultant d'une pression P sur une surface d'aire S vaut donc (transformation de formule) :

F = P×S

La direction est normale (perpendiculaire) à la surface ; le sens est celui de la poussée. Le point d'application, appelé « centre de poussée », est le centre C de la surface.

Caractéristiques de la résultante de la pression

Action	Point d'application	Direction	Sens	Intensité
$\vec \mathrm{F}_\mathrm{P}$	C (centre de la surface)	⊥ surface	poussée	P×S

Voir les exercices sur : Forces de pression.

Actions de contact

Une action de contact est une force créée par le contact entre deux pièces. On envisage principalement deux cas :

• les pièces sont liées par une liaison sphère-plan ;
• les pièces sont liées par une liaison pivot.

On peut faire l'étude pour chacune des 11 liaisons mécaniques (voir Modélisation - Les liaisons mécaniques), mais ces deux liaisons suffisent à traiter la plupart des problèmes.

Hypothèse

On considère des liaisons parfaites, c'est-à-dire sans adhérence ni frottement.

Les liaisons ont un jeu suffisant et sont lubrifiées, elles « n'accrochent » pas, ne grippent pas. On ne peut transmettre d'effort que par obstacle, pas par frottement, on exclue donc de l'étude les transmissions par courroies asynchrones (lisses), par galet, les embrayages et freins.

Convention

Soient un solide rep. 1 et un solide rep. 2 en liaison au point A. On note :

• $\vec \mathrm{A}_{1/2}$ l'action du solide 1 sur le solide 2 ;
• $\vec \mathrm{A}_{2/1}$ l'action du solide 2 sur le solide 1.

Les actions mécaniques sont réciproques

Il s'agit bien de deux actions différentes. C'est une question de point de vue : si une personne 1 pousse sur une personne 2, alors la personne 2 pousse elle aussi sur la personne 1. C'est la notion de réciprocité.

Début d'un théorème

Principe des actions réciproques

Si un solide 1 exerce une action sur un solide 2, alors 2 exerce une action sur 1 qui est opposée, a la même direction et la même intensité :

$\vec \mathrm{A}_{1/2} = -\vec \mathrm{A}_{2/1}$.

Fin du théorème

Ce principe est également appelé « principe des actions mutuelles » ou « 3^e loi de Newton ».

Liaison sphère-plan

Action de contact dans le cas d'une liaison sphère-plan

Rappel

La liaison sphère-plan, ou liaison ponctuelle, est la liaison ayant un seul degré de liaison : elle ne bloque qu'un degré de liberté, la translation perpendiculaire au plan de contact. Cela correspond à une butée, à un pied de table, …

Début d'une propriété Propriété

La force dans le cas d'une liaison sphère-plan est nécessairement normal (perpendiculaire) au plan d'appui. Le point d'application est le point de contact entre les solides.

Début de la propriété

On ne connaît que ces deux caractéristiques de la force. Les autres — sens, intensité (norme) — sont inconnus au début ; le but de la statique est précisément de déterminer les caractéristiques inconnues. Comme on ne connaît pas le sens, on représente la force par une double-flèche « ↔ » supportée par un trait d'axe « ⋅ — ⋅ — »

Dans le cas illustré ci-contre (contact en A entre les pièces 1 et 2, normale selon l'axe $\vec z$), le tableau bilan est :

Caractéristiques des actions mécaniques

Action	Point d'application	Direction	Sens	Intensité
$\vec{\mathrm{A}}_{2/1}$	A	$\vec z$	?	?

Contact biponctuel

On pourrait penser connaître le sens, puisqu'une pièce en contact ne peut que pousser (sauf collage). Il faut bien comprendre que le symbole indique la nature du contact — un point — et la normale au plan, mais pas comment se contact est fait. On peut par exemple avoir un contact double, « biponctuel » ; en raison du jeu, il n'y a réellement qu'un seul contact à la fois, mais il peut être d'un côté ou de l'autre.

Liaison pivot

Action mécanique transmissible par une liaison pivot

Rappel

La liaison pivot correspond à une charnière. Elle n'a qu'un degré de liberté et cinq degrés de liaison.

Le fait de savoir que l'on a une liaison pivot ne permet pas de savoir quoi que ce soit sur les caractéristiques de la force, hormis le point d'application qui est le centre de la liaison.

Graphiquement, la force totalement inconnue est représentée par une flèche brisée « ↯ », indiquant par là que l'on ne connaît pas la direction. Le tableau des caractéristiques contient trois points d'interrogation.

Caractéristiques des actions mécaniques

Action	Point d'application	Direction	Sens	Intensité
$\vec{\mathrm{A}}_{2/1}$	A	?	?	?

Simplification des problèmes plans

Les objets sont en volume, les forces sont réparties dans l'espace. Mais dans un certain nombre de cas, on peut peut « mettre à plat » le problème et considérer que tout se passe dans un plan : c'est la « simplification des problèmes plans ».

Début d'une propriété Propriété

Si un problème est symétrique par rapport au plan $(\mathrm{O}, \vec x, \vec y)$, on peut appliquer la simplification des problèmes plans dans le plan $(\mathrm{O}, \vec x, \vec y)$ : on considère que tous les points d'application sont dans ce plan ; on considère que les forces sont coplanaire à ce plan.

Début de la propriété

Équivalence des liaisons

Un certain nombre de liaisons sont équivalentes à ces deux cas grâce à la simplification des problèmes plans :

• équivalent à une liaison sphère-plan de normale $\vec y$ :
  • liaison linéaire rectiligne d'axe $\vec z$ et de normale $\vec y$,
  • liaison linéaire annulaire d'axe $\vec y$ ;
• équivalent à une liaison pivot d'axe $\vec z$ :
  • liaison rotule,
  • liaison pivot glissant d'axe $\vec z$,
  • liaison linéaire annulaire d'axe $\vec z$.

Isolement d'un solide

L'étape fondamentale d'une étude de statique est l'isolement d'un solide.

Début d'une définition

Isolement d'un solide

Isoler un solide, c'est représenter ce solide seul. Cela permet de faire le bilan des actions mécaniques extérieures qui s'exercent sur le solide, c'est-à-dire de recenser les 3P :

• poids ;
• pression de fluides ;
• points de contact (actions de contact).

Fin de la définition

Voir les exercices sur : Isolement d'un solide.

Activité 3

Isoler une voiture en train de rouler sur une route horizontale. Le problème est symétrique dans le plan sagittal (plan vertical séparant la voiture en deux moitiés gauche-droite), et l'on supposera que la liaison entre les roues arrières (roues libres) et le sol est une liaison idéale.

Solution

Isolement de la voiture

On recense les actions mécaniques extérieures :

• poids : poids du véhicule $\vec \mathrm{P}$ ;
• pression : frottement de l'air (vent relatif) $\vec \mathrm{F}_\mathrm{f}$ ;
• points de contact : contact du sol 0 avec les roues de la voiture 1 en A et en B.

Caractéristiques des actions mécaniques

Action	Point d'application	Direction	Sens	Intensité
$\vec \mathrm{P}$	G	|	↓	mg
$\vec \mathrm{F}_\mathrm{f}$	centre de la face avant	—	←	déterminé par la vitesse
$\vec \mathrm{A}_{0/1}$	A	|	?	?
$\vec \mathrm{B}_{0/1}$	B	?	?	?

 

Moment

Le moment est donc une action mécanique « tournante ».

Loi des leviers

Utilisation d'un levier pour soulever une commode

Un levier est une machine simple permettant d'amplifier un effort. Pour produire une force F₁ à l'extrémité du levier, l'opérateur doit fournir une force F₂ vérifiant la loi des leviers :

Début d'un théorème

Loi des leviers

F₁×d₁ = F₂×d₂

Les distances d₁ et d₂ sont les bras de levier : distance du pivot à la ligne d'action de la force, pris perpendiculairement à la ligne d'action.

Fin du théorème

On a donc

$\mathrm{F}_1 = \frac{d_2}{d_1}\mathrm{F}_2,$

le levier amplifie la force d'un facteur d₂/d₁.

Moment d'une force

Grâce à un levier, une force peut produire un effort en rotation.

Orientation du plan : sens positif

Début d'une définition

Moment d'une force

Le moment d'une force $\vec \mathrm{F}$ par rapport à un point de pivot A vaut

$\mathcal{M}_\mathrm{A}(\vec \mathrm{F}) = \pm d \times \mathrm{F}$

où

• F est la norme de $\vec \mathrm{F}$, en newtons (N) ;
• d est le bras de levier de $\vec \mathrm{F}$ par rapport à A, en mètres (m) ;
• le signe dépend du sens de rotation induit par la force : + pour le sens direct (trigonométrique, antihoraire, ↺), - pour le sens indirect (↻).

Le moment s'exprime en newtons-mètres (Nm). On peut prendre le bras de levier en millimètres (mm), le moment est alors en newtons-millimètres (Nmm).

Fin de la définition

Mnémotechnique : le sens positif va de l'axe x vers l'axe y.

Voir les exercices sur : Moments.

Couple

Couple

Début d'une définition

Couple

Un couple est l'action combinée de deux forces $\vec \mathrm{F}_1$ et $\vec \mathrm{F}_2$ de même direction, même norme, mais de sens opposés :

$\vec \mathrm{F}_1 = - \vec \mathrm{F}_2$.

Fin de la définition

Début d'une propriété Propriété

Un couple a une résultante nulle $\vec \mathrm{F}_1 + \vec \mathrm{F}_2 = \vec 0$. Le moment résultant par rapport à n'importe quel point est noté $\mathcal{C}$ et vaut $\mathcal{C} = \mathcal{M}_\mathrm{A}(\vec \mathrm{F}_1) + \mathcal{M}_\mathrm{A}(\vec \mathrm{F}_2) = \pm d\times \mathrm{F}$ où A est un point quelconque ; d est la distance séparant les droites d'action de $\vec \mathrm{F}_1$ et de $\vec \mathrm{F}_2$, pris perpendiculairement aux lignes d'action ; $\mathrm{F} = \| \vec \mathrm{F}_1 \| = \| \vec \mathrm{F}_2 \|$.

Début de la propriété

Le moment du couple est simplement appelé « couple ». On confond souvent les termes « moment » et « couple » : on parle de « couple moteur », de « couple résistant », de « couple de serrage ».

La notice d'utilisation d'une perceuse ou d'une visseuse-dévisseuse indique le couple, en général de l'ordre de 1 à 10 Nm pour une visseuse-dévisseuse sans fil, 100 Nm et plus pour une perceuse ou une boulonneuse à frappe tangentielle.

Moment transmis par contact

Une liaison appui plan (haut) et une liaison encastrement peuvent transmettre une force et un moment

Une pièce peut transmettre un moment à une autre pièce par contact. C'est le cas par exemple d'un arbre moteur qui transmet un moment du moteur à une roue (roue dentée, poulie). Le moment qu'exerce une pièce 1 sur une pièce 2 est noté $\mathcal{M}_{1/2}$.

Dans le cas des problème plans, un moment se représente graphiquement par une flèche tournante, ↺ ou ↻. Analytiquement, il s'exprime en Nm ou Nmm. Il s'agit en général d'un couple (transmission d'un moment sans force résultante).

La plupart du temps, le couple est transmis par l'intermédiaire d'une liaison encastrement. Un couple peut également être transmis par une liaison appui-plan, une liaison glissière, …

Notes pour les enseignants

La notion de centre de gravité concerne toutes les formations, mais on se contente la plupart du temps de donner sa position. Le calcul du centre de gravité d'un ensemble, ou bien la détermination du centre de gravité d'une tôle, concerne essentiellement les chaudronniers.

La réciprocité des actions mécaniques est générale, mais il vaut mieux se limiter au seul cas des actions de contact, qui est intuitif ; il n'est pas utile, voire peut-être contre-productif, de parler de l'attraction gravitationnelle qu'exerce un objet sur la Terre…

La notion de liaisons équivalente dans le cas de problèmes plans peut être introduite au cours d'exercices plutôt qu'en cours magistral.

La notion de moment transmissible n'est pas utile à tous les domaines.

Voir aussi

• Barycentre

Notes

Mécanique pour l'enseignement technique industriel

Mouvement plan

Statique - Principe fondamental de la statique