Fonctions convexes/Définition et premières propriétés

Début de la boite de navigation du chapitre

fin de la boite de navigation du chapitre

Dans tout ce chapitre, $I$ et $J$ désignent des intervalles de ℝ.

Définition

On dit qu'une application $f:I\to \mathbb {R}$ est

• convexe sur $I$ si :

  $\forall (a,b)\in I^{2}\quad \forall \lambda \in \left[0,1\right]\qquad f\left(\lambda a+(1-\lambda )b\right)\leqslant \lambda f(a)+(1-\lambda )f(b)$ ;

• strictement convexe sur $I$ si, pour $a\neq b$ et $\lambda \in \left]0,1\right[$, on a même : $f\left(\lambda a+(1-\lambda )b\right)<\lambda f(a)+(1-\lambda )f(b)$.

Les inégalités de la définition sont connues sous les noms d’inégalité de convexité et d’inégalité de convexité stricte.

Ces définitions s’appliquent à des fonctions qui ne sont pas forcément dérivables. Dans le cas où la fonction est dérivable ou mieux admet une dérivée seconde, nous verrons que l’on peut trouver des caractérisations plus simples des fonctions convexes et une condition suffisante de convexité stricte.

Définition

On dit qu'une application $f:I\to \mathbb {R}$ est concave (resp. strictement concave) sur $I$ si $-f$ est convexe (resp. strictement convexe) sur $I$.

Nous allons étudier maintenant quelques propriétés des fonctions convexes.

Propriété 1

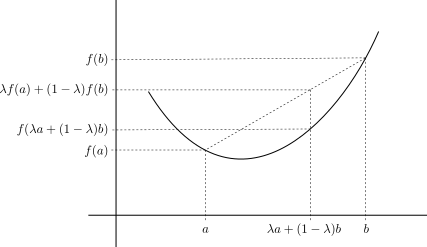
Une application $f:I\to \mathbb {R}$ est convexe sur $I$ si et seulement si pour tous points $A$ et $B$ de sa courbe représentative, l’arc ${\overset {\displaystyle \frown }{AB}}$ est en-dessous de la corde $[AB]$.

Il n’y a pas vraiment de démonstration à faire ici. Cette propriété n’est en fait que la traduction visuelle de la définition que nous avons donnée d’une fonction convexe.

Nous allons essayer de mieux voir ceci à travers les deux lemmes suivants :

Début d'un lemme

Lemme 1

Soit $(a,b)\in \mathbb {R} ^{2}$ avec $a<b$. Un réel $x$ vérifie $a\leqslant x\leqslant b$ si, et seulement si, il s'écrit sous la forme :

$x=\lambda a+(1-\lambda )b$ avec $\lambda \in \left[0,1\right]$.

Fin du lemme

'Démonstration'

Tout réel $x$ s'écrit sous la forme $x=\lambda a+(1-\lambda )b$ pour un unique $\lambda \in \mathbb {R}$, car

$x=ta+(1-t)b\Leftrightarrow x-b=t(a-b)\Leftrightarrow t=\lambda$, avec $\lambda :={\frac {x-b}{a-b}}={\frac {b-x}{b-a}}$.

Cette unique solution $\lambda$ vérifie :

${\begin{aligned}a\leqslant x\leqslant b&\Leftrightarrow a\leqslant \lambda a+(1-\lambda )b\leqslant b\\&\Leftrightarrow a-b\leqslant \lambda (a-b)\leqslant 0\\&\Leftrightarrow 0\leqslant \lambda (b-a)\leqslant b-a\\&\Leftrightarrow 0\leqslant \lambda \leqslant 1.\end{aligned}}$

 

Début d'un lemme

Lemme 2

Soient $A$ le point de coordonnées $(a,f(a))$ et $B$ le point de coordonnées $(b,f(b))$.

Un point appartient au segment $[AB]$ si et seulement si ses coordonnées sont de la forme :

$(\lambda a+(1-\lambda )b,\lambda f(a)+(1-\lambda )f(b))$, avec $\lambda \in \left[0,1\right]$.

Fin du lemme

'Démonstration'

Notons $(a,a')$ les coordonnées de $A$ et $(b,b')$ celles de $B$. Les points du segment $[AB]$ sont, par définition, tous les barycentres des deux points $A$ et $B$, pondérés respectivement par deux coefficients $\alpha ,\beta$ de même signe tels que $\alpha +\beta \neq 0$, c'est-à-dire les points de coordonnées $\left({\frac {\alpha }{\alpha +\beta }}a+{\frac {\beta }{\alpha +\beta }}b,{\frac {\alpha }{\alpha +\beta }}a'+{\frac {\beta }{\alpha +\beta }}b'\right)=(\lambda a+(1-\lambda )b,\lambda a'+(1-\lambda )b')$, avec $\lambda ={\frac {\alpha }{\alpha +\beta }}\in \left[0,1\right]$.

 

Grâce aux deux lemmes qui précèdent et au schéma qui suit, nous comprenons maintenant mieux que la propriété 1 n’est que la traduction de la définition d’une fonction convexe.

Propriété 2 (inégalité des pentes)

Si une application $f:I\to \mathbb {R}$ est convexe alors, pour tous $a<c<b$ dans $I$ :

${\frac {f(c)-f(a)}{c-a}}\leq {\frac {f(b)-f(a)}{b-a}}\leq {\frac {f(b)-f(c)}{b-c}}$

et par conséquent,

${\frac {f(c)-f(a)}{c-a}}\leq {\frac {f(b)-f(c)}{b-c}}$.

Réciproquement, si l'une des trois inégalités est vérifiée pour tous $a<c<b$ dans $I$ alors $f$ est convexe.

L'inégalité des pentes a été démontrée dans le chapitre « Convexité » de la leçon sur les fonctions d’une variable réelle.

Propriété 3

Soit une application $f:I\to \mathbb {R}$. Pour tout $a\in I$, on définit l’application :

$h_{a}:I\setminus \{a\}\to \mathbb {R} ,\ x\mapsto {\frac {f(x)-f(a)}{x-a}}$.

Alors, les cinq propriétés suivantes sont équivalentes :

1. $f$ est convexe sur $I$ ;
2. pour tout $a\in I$, $h_{a}$ est croissante sur $I\cap \left]a,+\infty \right[$ ;
3. pour tout $a\in I$, $h_{a}$ est croissante sur $I\cap \left]-\infty ,a\right[$ ;
4. pour tout $a\in I$, les valeurs de $h_{a}$ sur $I\cap \left]-\infty ,a\right[$ sont inférieures à celles sur $I\cap \left]a,+\infty \right[$ ;
5. pour tout $a\in I$, $h_{a}$ est croissante sur $I\setminus \{a\}$.

'Démonstration'

Les propriétés 2, 3 et 4 sont respectivement équivalentes aux trois inégalités des pentes, donc chacune est équivalente à la convexité de $f$. Par conséquent, la cinquième l'est aussi.

 

Propriété 4

Si $f:I\to \mathbb {R}$ est convexe, alors $I$ est réunion de trois sous-intervalles consécutifs (dont certains peuvent être vides) tels que $f$ est strictement décroissante sur le premier, constante sur le deuxième et strictement croissante sur le troisième.

'Démonstration'

Faites ces exercices : Fonctions d'une variable réelle — Convexité : Exercice 7.

 

Propriété 5

Soit $f:I\to \mathbb {R}$ une fonction convexe.

1. Si $\sup(I)=+\infty$ alors ou bien $f$ est décroissante, ou bien $\lim _{x\to +\infty }f(x)=+\infty$.
2. Si $\inf(I)=-\infty$ alors ou bien $f$ est croissante, ou bien $\lim _{x\to -\infty }f(x)=+\infty$.
3. Si $I=\mathbb {R}$ et si $f$ est majorée, alors elle est constante.

'Démonstration'

1. Si $\sup(I)=+\infty$ et $f$ n'est pas décroissante alors, d'après la propriété 4, il existe $a\in I$ tel que sur $\left[a,+\infty \right[$, $f$ est strictement croissante, en particulier :
   $k:=f(a+1)-f(a)>0$.
   Or d'après la propriété 3, pour tout $x\geq a+1$, $h_{a}(a+1)\leq h_{a}(x)$, c'est-à-dire $k\leq {\frac {f(x)-f(a)}{x-a}}$, ou encore
   $f(x)\geq k(x-a)+f(a)$.
   Comme $\lim _{x\to \infty }k(x-a)+f(a)=+\infty$, on en déduit : $\lim _{x\to \infty }f(x)=+\infty$.
2. se démontre comme 1., ou s'en déduit par le changement de variable $t\mapsto -t$.
3. est une conséquence immédiate de 1. et 2.

 

Propriété 6

Toute fonction convexe sur un intervalle ouvert $I$ est continue sur $I$.

'Démonstration'

D'après la propriété 3, pour tout $\mu \in I$, la fonction « pente » $h_{\mu }$ est croissante.

Elle admet donc (d'après le théorème de la limite monotone) une limite à gauche et à droite en $\mu$ finies. Cela montre que $f$ est dérivable à gauche et à droite, donc continue.

 

Une fonction convexe sur un intervalle non ouvert peut être discontinue aux extrémités de cet intervalle. Par exemple, la fonction $f:\mathbb {R} _{+}\to \mathbb {R}$ définie par $f(0)=1\quad {\text{et}}\quad \forall x>0\quad f(x)=0$ est convexe sur $\mathbb {R} _{+}$ mais n’est pas continue en $0$.

Propriété 7

Soit $f$ une fonction convexe strictement monotone sur un intervalle ouvert $I$. Sur l'intervalle $f(I)$, $f^{-1}$ est

• convexe si $f$ est décroissante ;
• concave $f$ est croissante.

'Démonstration'

Le second point se déduit du premier en remplaçant $f$ par l'application $x\mapsto f(-x)$. Supposons donc désormais $f$ décroissante (strictement).

D’après la propriété 6, f, étant convexe sur l’intervalle ouvert I, sera continue sur I. Comme, de plus, f est strictement décroissante sur I, on en déduit que f est bijective sur I. Par conséquent f^-1 existe. Soit a, b ∈ f(I), posons c = f^-1(a) et d = f^-1(b).

Comme f est convexe, on a :

$\forall \lambda \in \left]0,1\right[\qquad f\left(\lambda c+(1-\lambda )d\right)\leqslant \lambda f(c)+(1-\lambda )f(d)$

f étant décroissante, f^–1 sera aussi décroissante et par conséquent, on en déduit :

$\forall \lambda \in \left]0,1\right[\qquad f^{-1}\left(\lambda f(c)+(1-\lambda )f(d)\right)\leqslant f^{-1}\left(f\left(\lambda c+(1-\lambda )d\right)\right)$

c’est-à-dire :

$\forall \lambda \in \left]0,1\right[\qquad f^{-1}\left(\lambda a+(1-\lambda )b\right)\leqslant \lambda f^{-1}(a)+(1-\lambda )f^{-1}(b)$

Ce qui montre que f^-1 est convexe.

 

Propriété 8

Soit $f:I\to J$ une fonction convexe. Pour toute fonction $g:J\to \mathbb {R}$,

• si $g$ est convexe et croissante alors la composée $g\circ f$ est convexe ;
• si $g$ est concave et décroissante alors $g\circ f$ est concave.

'Démonstration'

Le second point se ramène au premier en remplaçant $g$ par $-g$. Supposons donc désormais $g$ convexe et croissante.

Soient $a,b\in I$ et $\lambda \in \left[0,1\right]$. Par convexité de $f$,

$f\left(\lambda a+(1-\lambda )b\right)\leqslant \lambda f(a)+(1-\lambda )f(b)$

donc, par croissance de $g$,

$g\left(f\left(\lambda a+(1-\lambda )b\right)\right)\leqslant g\left(\lambda f(a)+(1-\lambda )f(b)\right)$

et en appliquant la convexité de $g$ au second membre, on obtient :

$g\circ f\left(\lambda a+(1-\lambda )b\right)\leqslant \lambda g\circ f(a)+(1-\lambda )g\circ f(b)$.

 

Propriété 9

Si une fonction $k:I\to \left]0,+\infty \right[$ est logarithmiquement convexe, c'est-à-dire si $\ln \circ k$ est convexe, alors $k$ est convexe.

'Démonstration'

Soient $f:=\ln \circ k:I\to \mathbb {R}$ (convexe) et $g:=\exp :\mathbb {R} \to \mathbb {R}$ (la fonction exponentielle, croissante et convexe). D'après la propriété précédente, $g\circ f:I\to \mathbb {R}$ est convexe. Or $g\circ f=\exp \circ \ln \circ k=k$.

 

Le théorème suivant est démontré dans ce paragraphe car il s’applique à des fonctions convexes qui ne sont pas forcément dérivables. Mais compte tenu de l’importance de ce théorème, nous le reprendrons dans un chapitre spécialement consacré à ses applications.

Début d’un théorème

Théorème (Inégalité de Jensen)

Soit $f:I\to \mathbb {R}$ une fonction convexe. Pour tout (x₁, x₂, … , x_n) ∈ Iⁿ et pour toute famille (λ₁, λ₂, … , λ_n) ∈ (ℝ₊)ⁿ telle que λ₁ + λ₂ + … + λ_n = 1, on a :

$f\left(\sum _{i=1}^{n}\lambda _{i}x_{i}\right)\leqslant \sum _{i=1}^{n}\lambda _{i}f(x_{i})$.

Fin du théorème

'Démonstration'

Nous raisonnerons par récurrence sur n.

La propriété est triviale pour n = 1 et, plus généralement, lorsque l'un des λ_k vaut 1 (les autres étant alors nuls).

Supposons-la vraie pour n.

Soit (λ₁, λ₂,… λ_n+1) ∈ [0, 1[ⁿ⁺¹ tel que :

$\sum _{k=1}^{n+1}\lambda _{k}=1$

et soit (x₁, x₂, … , x_n+1) ∈ Iⁿ⁺¹.

Posons λ = 1 – λ_n+1 (strictement positif), puis

$x={\frac {\lambda _{1}x_{1}+\lambda _{2}x_{2}+\cdots +\lambda _{n}x_{n}}{\lambda }}$.

L’inégalité de convexité nous permet d’écrire :

$f\left(\sum _{i=1}^{n+1}\lambda _{i}x_{i}\right)=f\left(\sum _{i=1}^{n}\lambda _{i}x_{i}+\lambda _{n+1}x_{n+1}\right)=f\left(\lambda x+\lambda _{n+1}x_{n+1}\right)\leqslant \lambda f(x)+\lambda _{n+1}f(x_{n+1})$.

Par hypothèse de récurrence, on a :

${\begin{aligned}f(x)&=f\left({\frac {\lambda _{1}x_{1}+\lambda _{2}x_{2}+\cdots +\lambda _{n}x_{n}}{\lambda }}\right)\\&=f\left({\frac {\lambda _{1}}{\lambda }}x_{1}+{\frac {\lambda _{2}}{\lambda }}x_{2}+\cdots +{\frac {\lambda _{n}}{\lambda }}x_{n}\right)\\&\leqslant {\frac {\lambda _{1}}{\lambda }}f(x_{1})+{\frac {\lambda _{2}}{\lambda }}f(x_{2})+\cdots +{\frac {\lambda _{n}}{\lambda }}f(x_{n}).\end{aligned}}$

Par conséquent :

$f\left(\sum _{i=1}^{n+1}\lambda _{i}x_{i}\right)\leqslant \lambda f(x)+\lambda _{n+1}f(x_{n+1})\leqslant \lambda \left({\frac {\lambda _{1}}{\lambda }}f(x_{1})+{\frac {\lambda _{2}}{\lambda }}f(x_{2})+\cdots +{\frac {\lambda _{n}}{\lambda }}f(x_{n})\right)+\lambda _{n+1}f(x_{n+1})=\sum _{i=1}^{n+1}\lambda _{i}f(x_{i})$

et la propriété est vraie pour n + 1.

 

Propriété 10 : minorante affine

Soient $f:I\to \mathbb {R}$ une fonction convexe et $a$ un point intérieur à l'intervalle $I$. Alors, il existe $\alpha ,\beta \in \mathbb {R}$ tels que

$f(a)=\alpha a+\beta$ et $\forall x\in I\quad f(x)\geq \alpha x+\beta$.

'Démonstration'

Considérons la fonction croissante $h_{a}$ de la propriété 3 ci-dessus et $\alpha$ un réel tel que $\lim _{a^{-}}h_{a}\leq \alpha \leq \lim _{a^{+}}h_{a}$. Pour tout $x\in I$, on a $\alpha (x-a)\leq f(x)-f(a)$, avec égalité si $x=a$. La propriété est donc satisfaite en prenant $\beta =f(a)-\alpha a$.

 

Propriété 11

Soit $f:I\to \mathbb {R}$ une fonction continue. Pour que $f$ soit convexe sur $I$, il suffit qu'elle soit « faiblement convexe », c'est-à-dire que

$\forall (a,b)\in I^{2}\quad f\left({\frac {a+b}{2}}\right)\leq {\frac {f(a)+f(b)}{2}}$.

(L'expression « faiblement convexe » est empruntée à Emil Artin, The Gamma Function, Holt, Rinehart and Winston, 1964, 39 p. [lire en ligne], p. 5 .)

'Démonstration'

Cette démonstration, extraite de Constantin Nicolescu et Lars-Erik Persson, Convex Functions and their Applications: A Contemporary Approach, Springer, 2006 [lire en ligne], p. 10 , utilise le théorème de Weierstrass (ou « des bornes »). Pour une autre démonstration, voir le § « Possibilité de n'utiliser que des milieux » de l'article de Wikipédia sur les fonctions convexes.

Raisonnons par contraposée, c'est-à-dire supposons que $f$ (continue sur $I$) n'est pas convexe et montrons qu'alors elle n'est même pas « faiblement convexe ».

Par hypothèse, il existe un intervalle $[a,b]\subset I$ tel que le graphe de la restriction de $f$ à ce sous-intervalle ne soit pas entièrement en-dessous de la corde qui joint $(a,f(a))$ à $(b,f(b))$, c'est-à-dire tel que la fonction (continue)

$\varphi :[a,b]\to \mathbb {R} ,\,x\mapsto f(x)-{\frac {\left(f(b)-f(a)\right)x+b\,f(a)-a\,f(b)}{b-a}}$

vérifie :

$\gamma :=\max \varphi ([a,b])>0$.

Par continuité de $\varphi$, l'ensemble des points de $[a,b]$ en lesquels $\varphi$ atteint ce maximum $\gamma$ possède un plus petit élément, $c$.

Puisque $a\leq c\leq b$ et $\varphi (a)=\varphi (b)=0<\gamma =\varphi (c)$, on a $a<c<b$. Il existe donc $h>0$ tel que $a\leq c-h$ et $c+h\leq b$. Par définition de $\gamma$ et $c$,

$\varphi (c+h)\leq \gamma$, $\varphi (c)=\gamma$ et $\varphi (c-h)<\gamma$,

si bien que

$\varphi (c)>{\frac {\varphi (c-h)+\varphi (c+h)}{2}}$.

Par conséquent, $\varphi$ n'est pas « faiblement convexe ». On en déduit facilement que $f$ non plus.