Signaux physiques (PCSI)/Exercices/Introduction au monde quantique : particule libre confinée 1D
Puits quantique à une dimension[modifier | modifier le wikicode]
Puits quantique à une dimension de profondeur finie[modifier | modifier le wikicode]
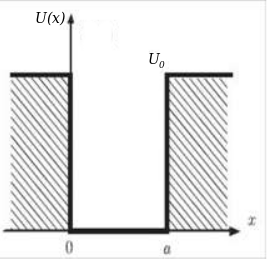
On considère une particule de masse décrite par une fonction d'onde évoluant dans un champ de force conservatif dérivant de l'énergie potentielle dont le diagramme en fonction de l'abscisse de la position est représenté ci-contre.
Dans un 1er temps, on considère un puits d'énergie potentielle de profondeur finie fixée à [1] diagramme ci-contre.
Écriture de l'équation de Schrödinger suivie par la particule[modifier | modifier le wikicode]
Écrire l'équation de Schrödinger[2] à une dimension suivie par la particule.
Préciser l'hamiltonien de la particule[3].
dans le cas où l'espace de localisation de l'onde de matière associée à la particule ainsi que ce dernier étant indépendant du temps soit «», l'équation de Schrödinger[2] se réécrit
Signification physique de l'équation de Schrödinger suivie par la particule[modifier | modifier le wikicode]
Expliquer physiquement la signification de l'équation de Schrödinger[2] suivie par la particule ainsi que
Expliquer physiquement la signification de la fonction d'onde [5].
L'équation de Schrödinger[2] est l'équation fondamentale de la mécanique quantique dans le cas non relativiste, c'est elle qui permet de décrire l'évolution à la fois temporelle et spatiale de la fonction d'onde ;
en mécanique quantique la fonction d'onde est le pendant du couple « position - quantité de mouvement » de la mécanique classique, l'équation de Schrödinger[2] remplaçant la r.f.d.n[6]. ;
en mécanique classique la connaissance des forces s'exerçant sur la particule avec celle du couple « position - quantité de mouvement » initiales permet de déterminer l'évolution temporelle du couple « position - quantité de mouvement » ,
en mécanique quantique la connaissance du champ d'énergie potentielle dans laquelle baigne la particule avec celle de la fonction d'onde initiale permet de déterminer l'évolution temporelle de la fonction d'onde à un facteur de phase près ;
la fonction d'onde contient toute l'information sur la particule étudiée en particulier la façon dont l'onde de matière associée à la particule se répartit dans l'espace à un instant donné ainsi que
la fonction d'onde contient toute l'information sur la particule étudiée en particulier l'évolution de cette répartition en fonction du temps,
la fonction d'onde contient toute l'information sur la particule étudiée c'est-à-dire la connaissance de la « densité linéique de probabilité de présence » ;
la fonction d'onde contient toute l'information sur la particule étudiée c'est-à-dire le module carré de la fonction d'onde doit être de carré sommable, plus exactement, dans la mesure où la particule existe,
la fonction d'onde contient toute l'information sur la particule étudiée c'est-à-dire sa probabilité de présence sur tout l'axe doit être égale à soit «» ;
la fonction d'onde contient toute l'information sur la particule étudiée c'est-à-dire la connaissance de la fonction d'onde permet de calculer toutes les valeurs moyennes utiles comme
la fonction d'onde contient toute l'information sur la particule étudiée c'est-à-dire la connaissance de la fonction d'onde permet de calculer celle de la position sur l'axe à l'instant égale à
la fonction d'onde contient toute l'information sur la particule étudiée c'est-à-dire la connaissance de la fonction d'onde permet de calculer «».
Conséquences de l'indépendance de l'hamiltonien de la particule relativement au temps[modifier | modifier le wikicode]
Sachant que l'hamiltonien de la particule[3] est ici indépendant du temps, quelle forme prend la fonction [7] ?
En déduire l'expression de l'équation de Schrödinger[2] indépendante du temps[7].
Dans la mesure où l'opérateur hamiltonien [3] est indépendant du temps, on peut rechercher la solution de l'équation de Schrödinger[2] « » sous la forme d'un produit de fonctions de variables séparées c'est-à-dire «» ce qui conduit à «» et permet de séparer les variables en divisant les deux membres par soit, après simplification évidente dans chaque membre, «» ;
sachant que la seule fonction qui soit à la fois une fonction de seule et une fonction de seule, et étant des variables indépendantes, est la fonction constante et
notant cette valeur constante a priori arbitraire,
sachant l'équation de Schrödinger se sépare en deux équations dont la 1ère gère la partie spatiale de la fonction d'onde avec la position et
sachant l'équation de Schrödinger se sépare en deux équations dont la 2ème la partie temporelle de la fonction d'onde avec le temps ;
la forme normalisée de la 2ème équation étant une équation linéaire à cœfficient complexe du 1er ordre en homogène, admet pour « solution »[8] et
la forme normalisée de la 2ème équation étant une équation linéaire à cœfficient complexe du 1er ordre en homogène, admet pour « celle-ci compte-tenu du fait que le champ d'énergie potentielle est indépendant du temps devant correspondre à une probabilité de présence indépendante du temps, le module de doit aussi en être indépendant, ce qui nécessite que soit réel[9] ;
la forme normalisée de la 2ème équation étant une équation linéaire à cœfficient complexe du 1er ordre en homogène, admet pour « on pose donc chaque valeur de définissant une énergie possible de la particule et la partie temporelle de la fonction d'onde se réécrit «»[10] ;
en introduisant la grandeur précédemment définie comme énergie possible de la particule, la 1ère équation se réécrit «»[11]
en introduisant la grandeur précédemment définie comme énergie possible de la particule, la 1ère équation se réécrit équation aux valeurs propres de l'opérateur hamiltonien[3] ou encore,
en introduisant la grandeur précédemment définie comme énergie possible de la particule, la 1ère équation se réécrit en explicitant l'hamiltonien[3] «»
en introduisant la grandeur précédemment définie comme énergie possible de la particule, la 1ère équation se réécrit en explicitant l'hamiltonien équation de Schrödinger[2] indépendante du temps.
Détermination de la solution générale de l'équation de Schrödinger dépendante du temps à partir des solutions de l'équation de Schrödinger indépendante du temps[modifier | modifier le wikicode]
Expliquer pourquoi résoudre l'équation de Schrödinger[2] indépendante du temps permet de déduire la solution générale de l'équation de Schrödinger dépendante du temps.
Supposons que l'on ait résolu l'équation de Schrödinger[2] indépendante du temps, c'est-à-dire que l'on ait obtenu toutes las valeurs propres [12] de l'opérateur hamiltonien[3] ainsi que
Supposons que l'on ait résolu l'équation de Schrödinger indépendante du temps, c'est-à-dire que l'on ait obtenu toutes les fonctions propres associées[13],
à chaque « état propre » on peut définir la « fonction d'onde associée dépendante du temps »
à chaque « état propre » on connaît un ensemble de discret générateur de n'importe quelle fonction d'onde solution de l'équation de Schrödinger[2] dépendante du temps[14] ;
à chaque fonction d'onde particulière dépendante du temps construite à partir d'un état propre de l'hamiltonien[3] correspondant à une « densité linéique de probabilité de présence » indépendante du temps définit un état stationnaire de la particule ;
supposons que l'on connaisse la décomposition initiale de la fonction d'onde sur l'ensemble des états stationnaires de la particule par exemple « avec »
supposons que l'on déduit, du caractère linéaire de l'équation de Schrödinger[2] dépendante du temps, la fonction d'onde à un instant quelconque «».
Forme générale de la partie spatiale de la fonction d'onde de la particule, solution de l'équation de Schrödinger indépendante du temps[modifier | modifier le wikicode]
Le potentiel étant constant par morceau, quelle forme générale prend la fonction [15],[16] ?
Considérant un puits quantique de profondeur et de largeur plus exactement «», c'est-à-dire constant par morceaux,
Considérant un puits quantique de profondeur et de largeur on en déduit l'équation de Schrödinger[2] indépendante du temps réécrite sous forme normalisée
Considérant un puits quantique de profondeur et de largeur on en déduit «» c'est-à-dire
Considérant un puits quantique de profondeur et de largeur on en déduit une équation différentielle linéaire à cœfficient constant par morceaux du 2ème ordre en homogène sans 1er ordre,
Considérant un puits quantique de profondeur et de largeur on en déduit une équation différentielle linéaire dont la résolution se discute selon la valeur de :
Condition de quantification de l'énergie de la particule dans le cas où celle-ci est inférieure à la profondeur du puits[modifier | modifier le wikicode]
Il est possible de montrer que, pour satisfaire l’équation de Schrödinger[2] indépendante du temps, la fonction d'onde [21] doit être continue[22] ; de la même façon,
il est possible de montrer que, dans la mesure où la discontinuité de l'énergie potentielle est finie[23], la dérivée de la fonction d’onde par rapport à l'abscisse de localisation [24] est aussi continue[22].
On se place dans le cas où l'énergie est toujours inférieure à la profondeur du puits .
En écrivant les conditions de continuités des morceaux de fonction d'onde[21][16] aux barrières d'énergie potentielle ainsi que
En écrivant les conditions de continuités des morceaux de leur dérivée spatiale 1ère, puis
En écrivant la compatibilité de ces conditions, déterminer l'équation définissant la quantification de l'énergie puis
En écrivant la compatibilité de ces conditions, la résoudre numériquement avec les données suivantes : [25], , [26] et on rappelle
En écrivant la compatibilité de ces conditions, la résoudre numériquement avec les données suivantes : la constante réduite de Planck[27] [28].
Nous avons vu précédemment que, pour , la solution par morceaux est de forme avec ; ces morceaux de la solution, ainsi que leur dérivée spatiale 1ère, doivent être continus et la solution globale doit vérifier la condition de normalisation, l'application de ces cinq conditions permet de déterminer les quatre constantes ainsi que les valeurs possibles de c'est-à-dire la condition de quantification de l'énergie.
Continuités en :
- s'explicite en et
- conduit à ,
Continuités en :
- s'explicite en et
- conduit à ,
Condition de quantification : Les relations et écrites respectivement selon «» et «»
Condition de quantification : Les relations et sont compatibles si ou soit encore
Condition de quantification : Les relations et sont compatibles si et enfin ou [30] c'est-à-dire
Condition de quantification : Les relations et sont compatibles avec la relation de quantification suivante «».
Condition de quantification : Remarque : On peut transformer cette condition de quantification selon « avec » et
Condition de quantification : Remarque : On peut transformer en utilisant «» équation du 2ème degré en de discriminant et donc de solution «» ;
Condition de quantification : Remarque : cette forme de relation de quantification n'est pas utilisée dans la résolution numérique qui suit.
Résolution numérique de la condition de quantification : « En posant », les valeurs de acceptables sont solutions de «» soit encore,
Résolution numérique de la condition de quantification : « en définissant la variable », les valeurs de acceptables sont solutions de «» ;
Résolution numérique de la condition de quantification : on trace alors sur un même diagramme, en fonction de la variable , le graphe de et celui de , les abscisses des points d'intersection nous donnant les valeurs de permises et par suite celles de autorisées ;
Résolution numérique de la condition de quantification : on trace avec on trouve voir 1er diagramme ci-dessous à gauche ;
Résolution numérique de la condition de quantification : on trace avec l'intersection nous donne deux valeurs d'énergie permises[31] : «».
Résolution numérique de la condition de quantification : on trace avec on trouve voir 2ème diagramme ci-dessous à droite ;
Résolution numérique de la condition de quantification : on trace avec l'intersection nous donne quatre valeurs d'énergie permises : «».


Partie spatiale de la fonction d'onde de la particule, solution de l'équation de Schrödinger indépendante du temps, dans le cas où l'énergie de la particule est inférieure à la profondeur du puits[modifier | modifier le wikicode]
Préciser les formes que prennent alors les solutions dans les 3 zones de l'espace , et après les avoir normalisées globalement[32] ?
il ne reste plus qu'à écrire la condition de normalisation pour évaluer , à savoir «»[33] avec la définition, par morceaux, de la densité linéique de probabilité de présence
il ne reste plus qu'à écrire la condition de normalisation pour évaluer , à savoir «» ;
la condition de normalisation se réécrit «» soit
- pour la 1ère intégrale «»,
- pour la 3ème intégrale « »,
pour la 3ème intégrale nous allons simplifier le résultat de cette 3ème intégrale en utilisant l'« autre forme de condition de quantification de l'énergie » établie dans la remarque de la solution de la question précédente, à savoir une condition de quantification sous les deux formes complémentaires pour la 1ère condition et pour la 2ème, soit
pour la 3ème intégrale avec la 1ère condition «», avec d'où «» et
pour la 3ème intégrale avec la 2ème condition «», avec d'où «»
pour la 3ème intégrale soit finalement la même expression de 3ème intégrale pour les deux formes de condition de quantification «»[34] et - pour la 2ème intégrale il convient tout d'abord de linéariser l'expression à intégrer après développement du carré soit d'où la réécriture de
pour la 2ème intégrale «» soit finalement «»,
pour la 2ème intégrale nous allons simplifier le résultat de cette 2ème intégrale en utilisant l'« autre forme de condition de quantification de l'énergie » établie dans la remarque de la solution de la question précédente, à savoir une condition de quantification sous les deux formes complémentaires pour la 1ère condition et pour la 2ème, soit
pour la 2ème intégrale avec la 1ère condition «», ainsi que
pour la 2ème intégrale avec la 1ère condition «», d'où
pour la 2ème intégrale avec la 1ère condition «», « » et
pour la 2ème intégrale avec la 2ème condition «», ainsi que
pour la 2ème intégrale avec la 2ème condition «», d'où
pour la 2ème intégrale avec la 2ème condition «», «»
pour la 2ème intégrale soit finalement la même expression de 2ème intégrale pour les deux formes de condition de quantification «» ;
en utilisant l'« autre forme de condition de quantification de l'énergie » établie dans la remarque de la solution de la question précédente,
à savoir une condition de quantification sous les deux formes complémentaires
pour la 1ère condition et pour la 2ème, soit
en ajoutant toutes les contributions avec la 2ème condition «», après une 1ère factorisation par dans dans le but de faire apparaître la condition de quantification à utiliser, on obtient soit enfin, en utilisant la formule de trigonométrie « », «»
en ajoutant toutes les contributions la condition de normalisation se réécrit «» d'où une 2ème expression du cœfficient
finalement la solution par morceaux s'écrit «»[36] avec «» c'est-à-dire
Expression du taux de transmission à l'extérieur du puits à une distance a de chacune de ses frontières dans le cas où l'énergie de la particule est inférieure à la profondeur du puits[modifier | modifier le wikicode]
Dans le cas où l'énergie de la particule est à la profondeur du puits d'énergie potentielle large de , on définit le taux de transmission à l'extérieur du puits à une distancede chacune de ses frontières[37] par « pour la transmission à gauche » et « pour la transmission à droite », étant la fonction d'onde[21] de la particule au point d'abscisse ;
explicitez, en fonction des données du problème, chacun des taux de transmission à l'extérieur du puits à une distance de chacune de ses frontières et vérifiez qu'ils sont égaux ; commentez.
Faire l'application numérique pour les deux largeurs de puits d'énergie potentielle précédemment introduites et on rappelle les autres valeurs numériques [25], [26] et [28] ; commentez.
D'après la solution de la question précédente « sur l'intervalle » permet d'en déduire «» ; de même
D'après la solution de la question précédente « sur l'intervalle » permet d'en déduire «» ; ainsi
en accord avec la symétrie du problème relativement au point d'abscisse , milieu du segment joignant les deux frontières du puits d'énergie potentielle.
A.N. : Avec la largeur , nous avions trouvé deux valeurs d'énergie pour la particule «»[26] et «»[26], nous en déduisons le taux de transmission commun à l'extérieur du puits à la distance de chacune de ses frontières après avoir calculé pour chaque niveau d'énergie,
A.N. : Avec la largeur , avec le niveau d'énergie fondamental «»[26], nous obtenons soit «» d'où «» c'est-à-dire une transmission faible mais observable alors qu'elle est interdite en mécanique classique ;
A.N. : Avec la largeur , avec le niveau d'énergie excité «»[26], nous obtenons soit «» d'où «» c'est-à-dire une transmission encore petite mais nettement plus observable alors qu'elle est interdite en mécanique classique.
A.N. : Avec la largeur , nous avions trouvé quatre valeurs d'énergie pour la particule «»[26], «»[26], «»[26] et «»[26], nous en déduisons le taux de transmission commun à l'extérieur du puits à la distance de chacune de ses frontières après avoir calculé pour chacun des niveaux d'énergie,
A.N. : Avec la largeur , avec le niveau d'énergie fondamental «»[26], nous obtenons soit «» d'où «» c'est-à-dire une transmission excessivement faible quasi-observable ;
A.N. : Avec la largeur , avec le 1er niveau d'énergie excité «»[26], nous obtenons soit «» d'où «» c'est-à-dire une transmission encore excessivement petite et qui n'est guère plus observable ;
A.N. : Avec la largeur , avec le 2ème niveau d'énergie excité «»[26], nous obtenons soit «» d'où «» c'est-à-dire une transmission faible restant difficilement observable mais observable néanmoins alors qu'elle est interdite en mécanique classique ;
A.N. : Avec la largeur , avec le 3ème niveau d'énergie excité «»[26], nous obtenons soit «» d'où «» c'est-à-dire une transmission encore petite mais nettement plus observable alors qu'elle est interdite en mécanique classique.
Puits quantique à une dimension de profondeur infinie[modifier | modifier le wikicode]

Dans un 2ème temps, on considère un puits d'énergie potentielle de profondeur infinie[1] dont le diagramme en fonction de l'abscisse de la position est représenté ci-contre.
Partie spatiale de la fonction d'onde de la particule, solution de l'équation de Schrödinger indépendante du temps, en-deçà et au-delà des barrières[modifier | modifier le wikicode]
Que devient alors la fonction d’onde [21] en-deçà et au-delà des barrières[38] ?
L'équation de Schrödinger[2] indépendante du temps s'écrivant toujours «»[16] dans laquelle « l'énergie potentielle » et « l'énergie de la particule prend des valeurs positives donc comprises entre et »,
L'équation de Schrödinger indépendante du temps s'écrivant toujours la solution en deçà et au-delà des barrières[38] nécessite d'y évaluer la constante caractéristique , celle-ci quand caractérisant les deux zones hors puits, ce qui conduit aux solutions «[39] quand »[40] ;
en conclusion la solution de l'équation de Schrödinger[2] indépendante du temps en deçà et au-delà des barrières[38] est «» correspondant à des zones d'occupation interdites pour la particule.
Conditions aux limites que doit satisfaire la partie spatiale de la fonction d'onde de la particule, solution de l'équation de Schrödinger indépendante du temps à l'intérieur du puits[modifier | modifier le wikicode]
En utilisant le fait que la fonction d'onde [21] doit être continue aux interfaces, c'est-à-dire en et , écrire les conditions aux limites que doit satisfaire , solution de l'équation de Schrödinger[2] indépendante du temps à l'intérieur du puits.
La continuité de sur la frontière de gauche c'est-à-dire en conduit à «» soit, avec «»[41] «» ;
la continuité de sur la frontière de droite c'est-à-dire en conduit à «» soit, avec «»[41] «».
Condition de quantification de l'énergie de la particule à l'intérieur du puits d'énergie potentielle et expression de la partie spatiale de sa fonction d'onde, solution de l'équation de Schrödinger indépendante du temps[modifier | modifier le wikicode]
En imposant les conditions aux limites à la fonction d'onde [21] solution de l'équation de Schrödinger[2] indépendante du temps à l'intérieur du puits d'énergie potentielle,
En imposant les conditions aux limites à la fonction d'onde déterminer la condition de quantification de l'énergie de la particule ;
en utilisant la condition de normalisation de la fonction d'onde [21], déterminer l'expression de [16] à l'intérieur du puits d'énergie potentielle et
En imposant les conditions aux limites à la fonction d'onde commenter les résultats.
A.N. : on propose deux applications numériques pour lesquelles on rappelle la valeur de la constante de Planck[27] :
- un électron dans un puits d'énergie potentielle de profondeur infinie et de largeur [42],
- un proton dans un puits d'énergie potentielle de profondeur infinie et de largeur [43],
A.N. : déterminer, dans chaque exemple, l'écart entre les énergies du niveau fondamental et le 1er niveau excité puis
A.N. : comparer à l'ordre de grandeur de l'écart de ces énergies dans un atome et dans un noyau.
Pour , la fonction d'onde[21] à l'intérieur du puits d'énergie potentielle s'écrit «» avec «»[39] ;
Pour , en appliquant on en déduit d'où se réécrit «» ;
Pour , en appliquant on en déduit d'où la « condition de quantification de grandeur caractéristique de la particule à l'intérieur du puits »[44]
Pour , en appliquant on en déduit d'où la « condition de quantification de donnant les grandeurs quantifiées «» ;
Pour chaque valeur , valeur propre de l'hamiltonien de la particule[3] à l'intérieur du puits d'énergie potentielle, on associe une fonction propre [45] ;
Pour chaque valeur , il ne reste plus qu'à écrire la condition de normalisation pour évaluer , à savoir «»[33], intégrale se réduisant à «»[46] dans laquelle « est la densité linéique de probabilité de présence de la particule à l'intérieur du puits d'énergie potentielle » ;
« avec ».
Commentaires : On retrouve le résultat fondamental de la quantification de l'énergie d'une particule quand cette dernière est confinée ;
Commentaires : les valeurs propres d'énergie étant d'expression quadratique relativement au niveau d'énergie, ces valeurs sont d'autant plus écartés que le niveau est élevé et
Commentaires : les valeurs propres d'énergie étant inversement proportionnelles au carré de la largeur du puits d'énergie potentielle, ces valeurs sont d'autant plus resserrées que la largeur est grande ainsi que
Commentaires : les valeurs propres d'énergie étant inversement proportionnelles à la masse de la particule, ces valeurs sont d'autant plus resserrées que la masse est grande.
A.N. : on propose deux applications numériques pour lesquelles on rappelle la valeur de la constante de Planck[27] ;
A.N. : l'écart entre les énergies du niveau et valant «»
A.N. : un écart entre l'énergie du 1er état excité et celle de l'état fondamental «» :
A.N. : 1er exemple un électron dans un puits d'énergie potentielle de profondeur infinie et de largeur [42] donne un écart d'énergies entre le niveau fondamental et celui du 1er état excité soit finalement «»[26],
A.N. : 2ème exemple un proton dans un puits d'énergie potentielle de profondeur infinie et de largeur [43], donne un écart d'énergies entre le niveau fondamental et celui du 1er état excité soit finalement «»[51] ;
A.N. : on vérifie, dans le 1er exemple, l'ordre de grandeur des écarts séparant les niveaux d'énergie d'un électron dans un atome à savoir de quelques à quelques , un atome étant de rayon de l'ordre de pour l'atome d'hydrogène à quelques pour les plus complexes ;
A.N. : on vérifie, dans le 2ème exemple, l'ordre de grandeur des écarts séparant les niveaux d'énergie des nucléons dans un noyau à savoir de quelques à quelques , un noyau étant de rayon de l'ordre de pour le noyau d'hydrogène à quelques pour les plus complexes.
Représentation graphique des trois premières fonctions d'onde et du carré de leurs modules[modifier | modifier le wikicode]
Donner la représentation graphique des trois 1ères fonctions d’onde[21] et de leurs modules carrés c'est-à-dire à leurs densités linéiques de probabilité de présence associées.
Ci-dessous à gauche la représentation graphique des trois 1ères fonctions d'onde[21] d'une particule dans un puits d'énergie potentielle de profondeur infinie et de largeur :
Ci-dessous à gauche dans l'état fondamental d'énergie «», de fonction propre associée «»[21], représentation en rouge, ainsi que
Ci-dessous à gauche dans les deux 1ers états excités d'énergie «», de fonction propre associée «»[21], représentation en bleu et
Ci-dessous à gauche dans les deux 1ers états excités d'énergie «», de fonction propre associée «»[21], représentation en vert ;
Ci-dessous à droite la représentation graphique des trois 1ères densités linéiques de probabilité de présence d'une particule dans un puits d'énergie potentielle de profondeur infinie et de largeur :
Ci-dessous à droite dans l'état fondamental d'énergie «», de densité linéique de probabilité de présence «», représentation en rouge on remarque que celle-ci est maximale au centre de puits d'énergie potentielle ainsi que
Ci-dessous à droite dans les deux 1ers états excités d'énergie «», de densité linéique de probabilité de présence « », représentation en bleu on remarque que celle-ci est maximale en et alors qu'elle est nulle au centre du puits d'énergie potentielle et
Ci-dessous à droite dans les deux 1ers états excités d'énergie «», de densité linéique de probabilité de présence « », représentation en vert on remarque que celle-ci est maximale en , au centre du puits d'énergie potentielle et en alors qu'elle est nulle en et .


Interprétation physique des résultats précédents[modifier | modifier le wikicode]
Énergie fondamentale de la particule confinée dans ce puits et différence avec le résultat de mécanique classique[modifier | modifier le wikicode]
Quelle est la plus basse énergie que puisse atteindre une particule confinée dans le puits ?
En quoi cette énergie est-elle différente de celle que l’on trouverait en mécanique classique ?
L'énergie fondamentale de la particule confinée dans un puits d'énergie potentielle de profondeur infinie est »«[28] ;
elle a comme particularité d'être « non nulle » plus précisément strictement positive contrairement à ce qu'on trouve en mécanique classique où « l'énergie fondamentale classique est nulle », correspondant à l'immobilité de la particule.
Justification de la différence précédente par inégalité spatiale de Heisenberg[modifier | modifier le wikicode]
Montrer que la différence précédente est une conséquence directe de l'inégalité spatiale de Heisenberg[52],[53].
La particule étant confinée sur l'intervalle , l'incertitude quantique[54] sur sa position est majorée selon «»[55] et
La particule étant confinée sur l'intervalle , l'incertitude quantique[54] sur sa quantité de mouvement se déduisant de l'inégalité spatiale de Heisenberg[52] selon on obtient, en utilisant le majorant précédemment déterminé de l'incertitude quantique[54] sur la position, que l'incertitude quantique[54] sur la quantité de mouvement est minorée selon «» ;
La particule étant confinée sur l'intervalle , la définition de cette dernière étant , la valeur moyenne de sa quantité de mouvement étant [56] soit encorece qui, devant être vérifié par tout niveau d'énergie, doit l'être en particulier par le niveau fondamental ,
ce qui est le cas car ;
la valeur de ce minorant prouve effectivement que « l'énergie fondamentale est nécessairement non nulle ».
Signification physique de la partie spatiale de la fonction d'onde[modifier | modifier le wikicode]
Discuter la signification physique de la fonction d’onde [21],[16] associée à l'énergie de la particule dans l'état de niveau .
La fonction d’onde [21],[16], solution de l'équation de Schrödinger[2] indépendante du temps ou fonction propre de l'hamiltonien de la particule[3] associée à la valeur propre de l'énergie de cette dernière, n'a pas de signification physique propre ;
La fonction d’onde seul le carré de son module en a une, il définit la densité linéique de probabilité de présence [58],
La fonction d’onde seul le carré de son module en a une, ses zéros donnant les abscisses où la particule est interdite pour cette énergie et
La fonction d’onde seul le carré de son module en a une, ses maxima, les abscisses où on a le plus de chance de trouver la particule pour cette même énergie.
Évolution temporelle d'un état stationnaire[modifier | modifier le wikicode]
Expliquer comment va évoluer temporellement un état stationnaire et en quoi cela justifie cette appellation.
Supposons que la particule possède, à l'instant initial, l'énergie , une des valeurs propres de l'hamiltonien de la particule[3], la fonction d'onde de cette dernière à l'instant initial est alors la fonction propre [21],[16] de son hamiltonien[3] associée à l'énergie propre soit «» ;
Supposons que la particule possède, à un instant quelconque, la fonction d'onde de la particule , solution de l'équation de Schrödinger[2] dépendante du temps suivie par la particule d'énergie s'écritSupposons que la particule possède, à un instant quelconque, la densité linéique de probabilité de présence de la particule à cet instant «» est encore égale à « » soit finalement «», établissant son indépendance relativement au temps d'où l'appellation d'état stationnaire.
Remarque : La particule possédant une énergie parfaitement définie, l'incertitude quantique[54] sur son énergie est nulle soit ;
Remarque : selon l'inégalité temporelle de Heisenberg[52] [59] et tenant compte de la nullité de l'incertitude quantique[54] sur l'énergie, on en déduit que l'incertitude quantique[54] sur l'instant d'observation de la particule doit être , ce qui correspond effectivement à un état où l'instant d'observation de la particule ne peut être déterminé comme il ne peut l'être dans un état stationnaire.
Évolution temporelle d'un état correspondant à la superposition initiale de deux états stationnaires[modifier | modifier le wikicode]
Soit la fonction d'onde initiale associée à un état résultant d’une superposition quelconque de deux états stationnaires à l'instant initial .
Soit Comment va évoluer temporellement un tel état ?
Connaissant la fonction d'onde initiale associée à un état de la particule résultant de la superposition des deux états stationnaires d'énergie respective et soit «»[60], on en déduit la fonction d'onde à l'instant quelconque «»[61].
La densité linéique initiale de probabilité de présence de la particule «»[62] s'évalue selon «
»[63],[64] ;
soit finalement «»[63],[65].
Constatant que la densité linéique de probabilité de présence de la particule à l'instant est une fonction sinusoïdale du temps de pulsation donc de période , on en déduit que l'état « superposition initiale de deux états stationnaires » n'est pas un état stationnaire.
Remarque : Compte-tenu du fait que l'état « superposition initiale de deux états stationnaires d'énergie respective et » n'est pas stationnaire, la mesure de l'énergie associée à l'état n'est déterminable qu'avec une incertitude quantique[54] «»[66] ;
Remarque : de l'inégalité de Heisenberg temporelle[52] [59] où est l'incertitude quantique[54] sur l'instant d'observation, on en déduit «» et on obtient, en utilisant le majorant précédemment déterminé de l'incertitude quantique[54] sur l'énergie, que l'incertitude quantique[54] sur l'instant d'observation est minorée selon «»[28], en accord avec le fait que la densité linéique de probabilité de présence est sinusoïdale du temps de période d'oùNotes et références[modifier | modifier le wikicode]
- ↑ 1,0 et 1,1 La référence de l'énergie potentielle c'est-à-dire l'endroit où elle est choisie nulle étant fixée au fonds du puits.
- ↑ 2,00 2,01 2,02 2,03 2,04 2,05 2,06 2,07 2,08 2,09 2,10 2,11 2,12 2,13 2,14 2,15 2,16 2,17 2,18 2,19 et 2,20 Erwin Rudolf Josef Alexander Schrödinger (1887 - 1961) physicien, philosophe et théoricien scientifique autrichien est à l'origine du développement d'un des formalismes théoriques de la mécanique quantique connu sous le nom de mécanique ondulatoire ; la formulation de l'équation d'onde connue sous le nom d'équation de Schrödinger lui a valu de partager le prix Nobel de physique en avec Paul Dirac lequel a été honoré pour la découverte de formes nouvelles et utiles de la théorie atomique ; on doit encore à Erwin Schrödinger l'expérience de pensée proposée à Albert Einstein en et connue sous le nom chat de Schrödinger.
Paul Adrien Maurice Dirac (1902 - 1984) physicien et mathématicien britannique, colauréat du prix Nobel de physique en , on lui doit des avancées cruciales dans le domaine de la mécanique statistique et de la physique quantique des atomes, il démontra l'équivalence physique entre la mécanique ondulatoire de Schrödinger et la mécanique matricielle de Heisenberg, deux présentations de la même mécanique quantique et enfin, pour les besoins du formalisme quantique, il inventa la notion, sans fondement mathématique précis, connue de nos jours sous le nom de distribution de Dirac et dont la description rigoureuse fut établie par le mathématicien français Laurent Schwartz dans sa théorie des distributions ; Paul Dirac fut colauréat du prix Nobel de Physique en pour la découverte de formes nouvelles et utiles de la théorie atomique, l'autre moitié du prix Nobel étant décernée à Erwin Schrödinger pour la formulation de l'équation d'onde dite de Schrödinger.
Albert Einstein (1879 - 1955), physicien théoricien d'origine allemande, devenu apatride en puis suisse en ; on lui doit la théorie de la relativité restreinte publiée en , la relativité générale en ainsi que bien d'autres avancées dans le domaine de la mécanique quantique et la cosmologie ; il a reçu le prix Nobel de physique en pour son explication de l'effet photoélectrique. - ↑ 3,00 3,01 3,02 3,03 3,04 3,05 3,06 3,07 3,08 3,09 3,10 3,11 et 3,12 Voir le paragraphe « construction de l'opérateur linéaire hamiltonien d'une particule quantique massique non relativiste » du chap. de la leçon « Signaux physiques (PCSI) ».
- ↑ On rappelle que l'opérateur linéaire est l'opérateur linéaire du 2ème ordre « laplacien », l'indice signifiant que les dérivations se font à constant voir le paragraphe « définition du champ scalaire laplacien d'une fonction scalaire de l'espace par l'image de l'opérateur “nabla scalaire nabla” sur une fonction scalaire » du chap. de la leçon « Outils mathématiques pour la physique (PCSI) » ;
en repérage cartésien le laplacien s'écrit «» voir le paragraphe « expression du laplacien d'une fonction scalaire de l'espace en cartésien » du chap. de la leçon « Outils mathématiques pour la physique (PCSI) ». - ↑ On pourra pour cela faire un parallèle entre la mécanique quantique et la mécanique classique à travers le couple position-impulsion.
- ↑ Relation fondamentale de la Dynamique Newtonienne.
- ↑ 7,0 et 7,1 On notera la partie spatiale de la fonction d'onde.
- ↑ Voir le paragraphe « résolution d'une éuqation différentielle linéaire à cœfficients constants du 1er ordre homogène » du chap. de la leçon « Outils mathématiques pour la physique (PCSI) ».
- ↑ En effet si on définit , on en déduit d'où dépendant du temps sauf si .
- ↑ La constante précédemment inscrite dans sera maintenant incluse dans la partie spatiale de la fonction d'onde.
- ↑ Chaque valeur de c'est-à-dire chaque valeur d'énergie possible de la particule définit une valeur propre de l'hamiltonien, la fonction étant alors la fonction propre associée à la valeur propre de l'hamiltonien, voir le paragraphe « recherche des états propres de l'opérateur linéaire hamiltonien à énergie potentielle ne dépendant pas explicitement du temps, équation de Schrödinger indépendante du temps » du chap. de la leçon « Signaux physiques (PCSI) ».
- ↑ Nous supposons que l'ensemble des valeurs propres forme un ensemble discret, chaque valeur propre étant repérée par un nombre entier.
- ↑ Nous supposons qu'aucune valeur propre n'est dégénérée c'est-à-dire qu'à chaque valeur propre il n'existe qu'une fonction propre à un facteur multiplicatif près.
- ↑ La justification étant que s'identifie à la valeur de à l'instant .
- ↑ On distinguera les cas selon que l'énergie de la particule est supérieure ou inférieure à la valeur de .
- ↑ 16,0 16,1 16,2 16,3 16,4 16,5 et 16,6 Chaque partie spatiale de fonction d'onde étant définie à un facteur de phase près, nous choisissons ce facteur égal à ce qui correspond à une partie spatiale de fonction d'onde réelle.
- ↑ 17,0 et 17,1 Revoir le paragraphe « résolution d'une équation différentielle linéaire à cœfficients constants du 2ème ordre homogène sans terme du 1er ordre » du chap. de la leçon « Outils mathématiques pour la physique (PCSI) ».
- ↑ Dans la forme pour on a supprimé le terme car il entraînerait une divergence pour ;
dans la forme pour on a supprimé le terme car il entraînerait une divergence pour . - ↑ Dans la forme pour on aurait l'expression « avec » d'où une densité linéique de probabilité de présence sur cet intervalle de définition égale à « » avec devant être finie car représentant la probabilité de présence sur le demi-axe revoir le paragraphe « intégrales généralisées d'une fonction continue par morceaux sur un intervalle ouvert dont au moins une des bornes est infinie » du chap. de la leçon « Outils mathématiques pour la physique (PCSI) » ; or l'intégration résultat divergeant sauf si et ce qui correspond à l'impossibilité d'être sur ce demi-axe ;
Dans la forme pour on aurait l'expression « avec » et on démontre, de la même façon, la finitude de ssi et ce qui correspond à l'impossibilité d'être sur ce demi-axe. - ↑ A priori il y a la solution par morceaux de forme suivante « avec »
mais l'utilisation des relations de continuités précisées à la question « condition de quantification de l'énergie de la particule dans le cas où celle-ci est inférieure à la profondeur du puits » plus bas dans cet exercice à savoir continuité de la fonction d'onde et de sa dérivée spatiale 1ère aux bornes de domaines où il y a une discontinuité finie de l'énergie potentielle conduit à la nullité de tous les cœfficients d'où l'absence de solution, en effet :
mais la continuité en conduit à ;
mais la continuité en conduit à soit enfin ;
mais en égalant les deux expressions de en fonction de pour la 1ère et de pour la 2ème on obtient soit « » ;
mais en égalant les deux expressions de en fonction de pour la 1ère et de pour la 2ème on obtient soit « » ;
mais or ces deux expressions de en fonction de ne sont compatibles pour que si «» qui n'est jamais réalisé compte -tenu du fait que le 1er membre est toujours et le 2ème toujours d'où la seule solution possible est impliquant . - ↑ 21,00 21,01 21,02 21,03 21,04 21,05 21,06 21,07 21,08 21,09 21,10 21,11 21,12 21,13 21,14 21,15 et 21,16 Plus exactement la partie spatiale de la fonction d'onde.
- ↑ 22,0 et 22,1 Ceci même si l'énergie potentielle présente une discontinuité.
- ↑ Mathématiquement on dit que la discontinuité est de 1ère espèce.
- ↑ Plus exactement la dérivée de la partie spatiale de la fonction d'onde par rapport à l'abscisse de localisation.
- ↑ 25,0 et 25,1 C'est la masse d'un électron.
- ↑ 26,00 26,01 26,02 26,03 26,04 26,05 26,06 26,07 26,08 26,09 26,10 26,11 26,12 26,13 et 26,14 On rappelle .
- ↑ 27,0 27,1 et 27,2 Max Karl Ernst Ludwig Planck (1858 - 1947) physicien allemand à qui on doit principalement, vers , la théorie des quanta, théorie qui lui valut le prix Nobel de physique en .
- ↑ 28,0 28,1 28,2 28,3 28,4 et 28,5 On rappelle que .
- ↑ 29,0 et 29,1 En simplifiant haut et bas par .
- ↑ En simplifiant haut et bas par .
- ↑ Sachant que les valeurs de possibles sont nécessairement inférieures à , et que le graphe de ne dépend pas de , nous aurons plus de points d'intersection si le graphe de possède plus de discontinuités lesquelles permettent au graphe de passer de à sans variation d'abscisse, ceci étant réalisé si est plus grand, donc si est plus grande.
- ↑ C.-à-d. avoir écrit que la probabilité de présence de la particule sur tout l'axe est égale à .
- ↑ 33,0 et 33,1 Revoir la définition d'une « intégrale généralisée d'une fonction continue par morceaux sur un intervalle ouvert dont au moins une des bornes est infinie » du chap. de la leçon « Outils mathématiques pour la physique (PCSI) ».
- ↑ C'est aussi le même résultat que celui de la 1ère intégrale.
- ↑ 35,0 et 35,1 Cette dernière expression résultant de .
- ↑ 36,0 36,1 et 36,2 avec la 1ère condition de quantification et avec la 2ème .
- ↑ C.-à-d. aux points d'abscisse et .
- ↑ 38,0 38,1 et 38,2 C.-à-d. dans les 2 zones de l'espace et .
- ↑ 39,0 et 39,1 Voir la solution de la question « forme générale de la partie spatiale de la fonction d'onde de la particule, solution de l'équation de Schrödinger indépendante du temps » plus haut dans cet exercice.
- ↑ En effet pour , l'abscisse étant négative, quand et pour , l'abscisse étant positive, quand .
- ↑ 41,0 et 41,1 Si on ne suppose pas, a priori, la continuité de la fonction d'onde laquelle est néanmoins toujours réalisée l'intervalle de définition de la fonction d'onde en-deçà et au-delà des frontières du puits d'énergie potentielle est ouvert sur la frontière.
- ↑ 42,0 et 42,1 L'angström «» est une unité bien adaptée aux dimensions de l'atome, elle a été choisie pour rendre hommage à « Anders Jonas Ångström (1814 - 1874), astronome et physicien suédois du XIXème siècle, un des fondateurs de la spectroscopie ».
- ↑ 43,0 et 43,1 On rappelle lire « fentomètre » pour sous-multiple de l'unité de longueur du Système international SI bien adapté aux dimensions du noyau ou
On rappelle lire « fermi » pour appellation historique en hommage à « Enrico Fermi (1901 - 1954), physicien italien naturalisé américain, ayant reçu le prix Nobel de physique en pour sa démonstration de l'existence de nouveaux éléments radioactifs produits par bombardements de neutrons, et pour sa découverte des réactions nucléaires créées par les neutrons lents ». - ↑ En effet conduirait à à l'intérieur du puits d'énergie potentielle c'est-à-dire à l'impossibilité pour la particule d'être d'énergie , énergie que l'on a supposée pour cette particule.
- ↑ pouvant dépendre a priori de est noté .
- ↑ Compte-tenu de l'impossibilité pour la particule d'être à l'extérieur du puits d'énergie potentielle, correspondant à la nullité de la fonction d'onde à l'extérieur du puits d'énergie potentielle.
- ↑ En effet la condition de quantification de est et .
- ↑ On constate que ne dépend pas de .
- ↑ On rappelle qu'une fonction d'onde et donc aussi la partie spatiale de la fonction d'onde étant définie à un facteur de phase près, on peut choisir n'importe quel signe dans le cas où elle est réelle.
- ↑ On vérifie que tous les niveaux d'énergie sont non dégénérés c'est-à-dire qu'il n'existe qu'une seule fonction propre à un facteur de phase près par valeur propre d'énergie.
- ↑ On rappelle .
- ↑ 52,0 52,1 52,2 et 52,3 Werner Heisenberg (1901 - 1976) physicien allemand, l'un des fondateurs de la mécanique quantique, a obtenu le prix Nobel de physique en pour la création d'une forme de mécanique quantique connue sous le nom de mécanique matricielle, dont l’application a mené, entre autres, à la découverte des variétés allotropiques de l'hydrogène le dihydrogène existe sous deux formes allotropiques « ortho » où les spins sont et « para » où ils sont anti, le dihydrogène ortho étant présent à à température élevée et sa proportion quand sa température .
- ↑ Voir le paragraphe « généralisation à la matière de l'inégalité de Heisenberg spatiale » du chap. de la leçon « Signaux physiques (PCSI) »
- ↑ 54,00 54,01 54,02 54,03 54,04 54,05 54,06 54,07 54,08 54,09 54,10 54,11 et 54,12 On parle d'incertitude « quantique » car c'est une incertitude théorique contenue dans les principes de la mécanique quantique, et non une incertitude « expérimentale ».
- ↑ En effet la valeur moyenne de l'abscisse de la particule est correspondant au maximum de densité linéique de probabilité de présence et son incertitude quantique définie selon donne sachant que .
- ↑ En effet ayant une même probabilité d'avoir la valeur et , nous en déduisons une valeur moyenne nulle.
- ↑ C.-à-d. la valeur moyenne du carré de la quantité de mouvement en fonction de l'incertitude quantique sur cette dernière.
- ↑ Le module devient inutile dans la mesure où on a choisi, la partie spatiale de la fonction d'onde, réelle.
- ↑ 59,0 et 59,1 Voir le paragraphe « en complément : inégalité de Heisenberg temporelle » du chap. de la leçon « Signaux physiques (PCSI) ».
- ↑ et étant les fonctions propres de l'hamiltonien de la particule associées respectivement aux valeurs propres et .
- ↑ Ceci résultant du caractère linéaire de l'équation de Schrödinger dépendante du temps.
- ↑ 62,0 et 62,1 On rappelle que le complexe conjugué de est noté voir le paragraphe « notion de complexe conjugué » du chap. de la leçon « Outils mathématiques pour la physique (PCSI) ».
- ↑ 63,0 et 63,1 Avec et .
- ↑ En effet .
- ↑ En effet .
- ↑ La mesure de l'énergie devant donner un résultat compris entre les deux bornes et avec une valeur moyenne pouvant être quelconque entre ces deux bornes, son incertitude quantique définie selon donne sachant que .
- ↑ C.-à-d. l'incertitude quantique sur l'instant d'observation est au moins de l'ordre de grandeur d'un dixième de la période de variation de la densité linéique de probabilité de présence.












![{\displaystyle \;{\widehat {\mathcal {H}}}\!\left[\;\right]\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d0cef9d50948b360b177eb23028ad30f1f3eb4f)

![{\displaystyle \;-{\dfrac {\hbar ^{2}}{2\;m}}\;\Delta _{t}\!\left[{\underline {\psi }}(M,\,t)\right]+U(M,\,t)\;{\underline {\psi }}(M,\,t)=i\;\hbar \left({\dfrac {\partial {\underline {\psi }}}{\partial t}}\right)_{\!\!M}(M,\,t)\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/56d9210b7ef17c8ba2fe26fff704f0b8ed25f3e6)

![{\displaystyle \;-{\dfrac {\hbar ^{2}}{2\;m}}\;\left[{\dfrac {\partial ^{2}{\underline {\psi }}}{\partial x^{2}}}\right]_{\!t}(x,\,t)+U(x)\;{\underline {\psi }}(x,\,t)=i\;\hbar \left({\dfrac {\partial {\underline {\psi }}}{\partial t}}\right)_{\!\!x}(x,\,t)\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/47dd648771baeccf06b377ae3b061f02b8af5f19)
![{\displaystyle \;{\widehat {\mathcal {H}}}\!\left[\;\right]=\left\lbrace -{\dfrac {\hbar ^{2}}{2\;m}}\;\left[{\dfrac {\partial ^{2}}{\partial x^{2}}}\right]_{\!t}+U(x)\times \right\rbrace \!\left[\;\right]\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3370d06aae7d2e78dbef47da1162ac74f12b1d7c)












![{\displaystyle \;{\widehat {\mathcal {H}}}\!\left[{\underline {\psi }}\right]\!(x,\,t)=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/169f586361bef3e7cec0186ea37e237d0a197323)
![{\displaystyle i\;\hbar \left({\dfrac {\partial }{\partial t}}\right)_{\!\!x}\!\left[{\underline {\psi }}\right]\!(x,\,t)\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d5b0c98ab47756da95aa5d2a1ecde61259411ad5)

![{\displaystyle \;\left\lbrace {\widehat {\mathcal {H}}}\!\left[{\underline {\Psi }}\right]\!(x)\right\rbrace {\underline {f}}(t)={\underline {\Psi }}(x)\left\lbrace i\;\hbar \;{\dfrac {d}{dt}}\!\left[{\underline {f}}\right]\!(t)\right\rbrace \;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/768c48f80fb0d33e9262b7be82ab0b4a2f5ca1e0)

![{\displaystyle \;{\dfrac {{\widehat {\mathcal {H}}}\!\left[{\underline {\Psi }}\right]\!(x)}{{\underline {\Psi }}(x)}}={\dfrac {i\;\hbar \;{\dfrac {d}{dt}}\!\left[{\underline {f}}\right]\!(t)}{{\underline {f}}(t)}}\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/edbd49c276ef13367894ac003cf84c35b0223509)


![{\displaystyle \;\left\lbrace {\begin{array}{c}{\widehat {\mathcal {H}}}\!\left[{\underline {\Psi }}\right]\!(x)={\underline {\alpha }}\;{\underline {\Psi }}(x)\\i\;\hbar \;{\dfrac {d}{dt}}\!\left[{\underline {f}}\right]\!(t)={\underline {\alpha }}\;{\underline {f}}(t)\end{array}}\right\rbrace \;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/78050c7d52f8d36d2c0aadf58ac676eab6a4ef12)

![{\displaystyle \;\color {transparent}{\left\lbrace {\begin{array}{c}{\widehat {\mathcal {H}}}\!\left[{\underline {\Psi }}\right]\!(x)={\underline {\alpha }}\;{\underline {\Psi }}(x)\\i\;\hbar \;{\dfrac {d}{dt}}\!\left[{\underline {f}}\right]\!(t)={\underline {\alpha }}\;{\underline {f}}(t)\end{array}}\right\rbrace }\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/265eea10b0480556225a9e94ddf08682316efdd6)












![{\displaystyle \;{\widehat {\mathcal {H}}}\!\left[{\underline {\Psi }}\right]\!(x)=E\;{\underline {\Psi }}(x)\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a50087588a380e92e39362ae2b9cc8c50520023)




![{\displaystyle \;\left[E_{n}\,;\,{\underline {\Psi }}_{n}(x)\right]\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f4cc85e7bacde14c4ace2a94b51019d64ec5bb1)


![{\displaystyle \;\color {transparent}{\left[E_{n}\,;\,{\underline {\Psi }}_{n}(x)\right]}\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f2bbf8c84a4d19856c1fe68094be7de0c3788b99)









![{\displaystyle \;{\dfrac {d^{2}{\underline {\Psi }}}{dx^{2}}}(x)-{\dfrac {2\;m}{\hbar ^{2}}}\left[U(x)-E\right]{\underline {\Psi }}(x)=0\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/22e9a835809e65ff5991d47f69a2a06b7cf45a41)

![{\displaystyle \;E\in \left]0,U_{0}\right[\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/36adf6869fcfb529b1c7517b0eecf441dfae57d8)
![{\displaystyle \;\Psi (x)=\left\lbrace {\begin{array}{l}\gamma \,\exp(-K\,x)\qquad \qquad \;{\text{ pour }}x\in \left[{\mathfrak {a}},+\infty \right[\\\alpha \,\sin(k\,x)+\beta \,\cos(k\,x){\text{ pour }}x\in \left]0,{\mathfrak {a}}\right[\\\delta \,\exp(K\,x)\qquad \qquad \quad {\text{ pour }}x\in \left]-\infty ,0\right]\end{array}}\right\rbrace \;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1fc6ebdc94de424c6fa96dfd461ca82092741eb6)

![{\displaystyle \;E\in \left]U_{0},+\infty \right[\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d817247cfece3e9619f554422fa6ea8ed2410153)
![{\displaystyle \;\Psi (x)=\left\lbrace {\begin{array}{l}0\qquad \qquad \qquad \qquad \quad \;\,{\text{ pour }}x\in \left[{\mathfrak {a}},+\infty \right[\\\alpha \,\sin(k\,x)+\beta \,\cos(k\,x){\text{ pour }}x\in \left]0,{\mathfrak {a}}\right[\\0\qquad \qquad \qquad \qquad \quad \;{\text{ pour }}x\in \left]-\infty ,0\right]\end{array}}\right\rbrace \;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93aca546b9279bd6846eb1e39a695769f0875fc2)

![{\displaystyle \;E\in \left]-\infty ,0\right[\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b48e4de8b05b5860c584d5b4f54d338447a3bcd)






![{\displaystyle \;E\in \left]0,U_{0}\right[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca606670eddaa8d20b3af6809ce23ede068a3d19)













![{\displaystyle \;\gamma =\left[\alpha \,\sin(k\,{\mathfrak {a}})+\beta \,\cos(k\,{\mathfrak {a}})\right]\exp(K\,{\mathfrak {a}})\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d56c9579f501ac36e86b12686d573c21ccefea0)
![{\displaystyle \;\gamma =\left[-\alpha \,\cos(k\,{\mathfrak {a}})+\beta \,\sin(k\,{\mathfrak {a}})\right]{\dfrac {k}{K}}\exp(K\,{\mathfrak {a}})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d572298bdc9e07831bfacaaa15c8fa19916a468)


![{\displaystyle \;\alpha \left[\sin(k\,{\mathfrak {a}})+{\dfrac {k}{K}}\,\cos(k\,{\mathfrak {a}})\right]=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a9fe11e73f4a543b476c3c8f1af282a77b6d0ff8)
![{\displaystyle \beta \left[{\dfrac {k}{K}}\,\sin(k\,{\mathfrak {a}})-\cos(k\,{\mathfrak {a}})\right]\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/033f67d7ca0baa1526292489059c1eafdfc8cc57)



![{\displaystyle \;\gamma =\alpha \,\left[\sin(k\,{\mathfrak {a}})+{\dfrac {K\,\sin(k\,{\mathfrak {a}})+k\,\cos(k\,{\mathfrak {a}})}{k\,\sin(k\,{\mathfrak {a}})-K\,\cos(k\,{\mathfrak {a}})}}\,\cos(k\,{\mathfrak {a}})\right]\exp(K\,{\mathfrak {a}})\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/615f30cea71cebad9259c7e3e0d78ce32116b05d)









![{\displaystyle \;2\,\cos(k\,{\mathfrak {a}})=\left[{\dfrac {k}{K}}-{\dfrac {K}{k}}\right]\sin(k\,{\mathfrak {a}})\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b3d4522ab6639c78f1502d85b3bcce782804ebc)






























![{\displaystyle \;\left]-\infty \,;\,0\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a35babb96e46691c46a7848529aa6799fa7e803e)
![{\displaystyle \;\left[0\,;\,{\mathfrak {a}}\right]\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f3ea77691d41f3757771dca22c3965c8bd10d36e)




![{\displaystyle \;\Psi (x)=\left\lbrace {\begin{array}{l}\alpha \,{\dfrac {{\dfrac {k}{K}}\,\exp \!\left[-K\,(x-{\mathfrak {a}})\right]}{{\dfrac {k}{K}}\,\sin(k\,{\mathfrak {a}})-\cos(k\,{\mathfrak {a}})}}\quad \;{\text{ pour }}x\in \left[{\mathfrak {a}},+\infty \right[\\\alpha \,\left[\sin(k\,x)+{\dfrac {k}{K}}\,\cos(k\,x)\right]{\text{ pour }}x\in \left]0,{\mathfrak {a}}\right[\\\alpha \,{\dfrac {k}{K}}\,\exp(K\,x)\qquad \qquad \quad \;{\text{ pour }}x\in \left]-\infty ,0\right]\end{array}}\right\rbrace \;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8456b8f3a163404bd9c86ce45d8c14dcd90a7de8)




![{\displaystyle \;{\mathcal {P}}_{l}(x)=\left[\Psi (x)\right]^{2}=\left\lbrace {\begin{array}{l}\alpha ^{2}\,{\dfrac {{\dfrac {k^{2}}{K^{2}}}\,\exp \!\left[-2\,K\,(x-{\mathfrak {a}})\right]}{\left[{\dfrac {k}{K}}\,\sin(k\,{\mathfrak {a}})-\cos(k\,{\mathfrak {a}})\right]^{2}}}\;{\text{ pour }}x\in \left[{\mathfrak {a}},+\infty \right[\\\alpha ^{2}\,\left[\sin(k\,x)+{\dfrac {k}{K}}\,\cos(k\,x)\right]^{2}\;{\text{ pour }}x\in \left]0,{\mathfrak {a}}\right[\\\alpha ^{2}\,{\dfrac {k^{2}}{K^{2}}}\,\exp(2\,K\,x)\qquad \qquad \;\;{\text{ pour }}x\in \left]-\infty ,0\right]\end{array}}\right\rbrace \;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/693e61080efbacfe61fd01e5c4f9b9530716ece9)
![{\displaystyle \;\displaystyle \int _{-\infty }^{0}{\dfrac {k^{2}}{K^{2}}}\,\exp(2\,K\,x)\,dx+\displaystyle \int _{0}^{\mathfrak {a}}\left[\sin(k\,x)+{\dfrac {k}{K}}\,\cos(k\,x)\right]^{2}\,dx+\displaystyle \int _{\mathfrak {a}}^{+\infty }{\dfrac {{\dfrac {k^{2}}{K^{2}}}\,\exp \!\left[-2\,K\,(x-{\mathfrak {a}})\right]}{\left[{\dfrac {k}{K}}\,\sin(k\,{\mathfrak {a}})-\cos(k\,{\mathfrak {a}})\right]^{2}}}\,dx={\dfrac {1}{\alpha ^{2}}}\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2877538a2755d205007c2cbe291cb3d4caa68142)
![{\displaystyle \;\displaystyle \int _{-\infty }^{0}{\dfrac {k^{2}}{K^{2}}}\,\exp(2\,K\,x)\,dx={\dfrac {k^{2}}{K^{2}}}\,\left[{\dfrac {\exp(2\,K\,x)}{2\,K}}\right]_{-\infty }^{0}={\dfrac {k^{2}}{2\,K^{3}}}\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55d58910955007caf63bdee3d39901cf8d6d18ed)
![{\displaystyle \;\displaystyle \int _{\mathfrak {a}}^{+\infty }{\dfrac {k^{2}}{K^{2}}}\,{\dfrac {1}{\left[{\dfrac {k}{K}}\,\sin(k\,{\mathfrak {a}})-\cos(k\,{\mathfrak {a}})\right]^{2}}}\,\exp \!\left[2\,K({\mathfrak {a}}-x)\right]dx={\dfrac {k^{2}}{K^{2}}}\,{\dfrac {1}{\left[{\dfrac {k}{K}}\,\sin(k\,{\mathfrak {a}})-\cos(k\,{\mathfrak {a}})\right]^{2}}}\,\left[{\dfrac {\exp \!\left\lbrace 2\,K({\mathfrak {a}}-x)\right\rbrace }{-2\,K}}\right]_{\mathfrak {a}}^{+\infty }={\dfrac {k^{2}}{2\,K^{3}}}\,{\dfrac {1}{\left[{\dfrac {k}{K}}\,\sin(k\,{\mathfrak {a}})-\cos(k\,{\mathfrak {a}})\right]^{2}}}=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/19200bcf4ac26e45122b64524477645242ad089a)
![{\displaystyle {\dfrac {1}{2\,K}}\,\left[{\dfrac {k}{k\,\sin(k\,{\mathfrak {a}})-K\,\cos(k\,{\mathfrak {a}})}}\right]^{2}\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8e004a4b8a13d2db93c319cb7fd6326176246f68)





![{\displaystyle \;{\dfrac {1}{2\,K}}\,\left[{\dfrac {1}{\sin(k\,{\mathfrak {a}})-{\dfrac {K}{k}}\,\cos(k\,{\mathfrak {a}})}}\right]^{2}={\dfrac {1}{2\,K}}\,\left[{\dfrac {1}{\sin(k\,{\mathfrak {a}})-\tan \!\left({\dfrac {k\,{\mathfrak {a}}}{2}}\right)\,\cos(k\,{\mathfrak {a}})}}\right]^{2}\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d11ea5b7551b3347328cd443a1ec5cfe14b1c338)


![{\displaystyle \;{\dfrac {1}{2\,K}}\,\left[{\dfrac {1}{\sin(k\,{\mathfrak {a}})-{\dfrac {K}{k}}\,\cos(k\,{\mathfrak {a}})}}\right]^{2}={\dfrac {k^{2}}{2\,K^{3}}}\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/05a419b6cb1ebf7537a3c2631ad0402cf639b311)
![{\displaystyle \;{\dfrac {1}{2\,K}}\,\left[{\dfrac {-{\dfrac {k}{K}}}{-{\dfrac {k}{K}}\,\sin(k\,{\mathfrak {a}})+\,\cos(k\,{\mathfrak {a}})}}\right]^{2}={\dfrac {1}{2\,K}}\,\left[{\dfrac {\tan \!\left({\dfrac {k\,{\mathfrak {a}}}{2}}\right)}{\tan \!\left({\dfrac {k\,{\mathfrak {a}}}{2}}\right)\,\sin(k\,{\mathfrak {a}})+\cos(k\,{\mathfrak {a}})}}\right]^{2}\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c03f5d6dfa443837a99c2f9fe64abfe879bc9d3)


![{\displaystyle \;\displaystyle \int _{\mathfrak {a}}^{+\infty }{\dfrac {k^{2}}{K^{2}}}\,{\dfrac {1}{\left[{\dfrac {k}{K}}\,\sin(k\,{\mathfrak {a}})-\cos(k\,{\mathfrak {a}})\right]^{2}}}\,\exp \!\left[2\,K({\mathfrak {a}}-x)\right]dx={\dfrac {k^{2}}{2\,K^{3}}}\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2ad685415749a87615e9b26b6990fc5235fe34f)
![{\displaystyle \;\left[\sin(k\,x)+{\dfrac {k}{K}}\,\cos(k\,x)\right]^{\!2}=\sin ^{2}(k\,x)+{\dfrac {k^{2}}{K^{2}}}\,\cos ^{2}(k\,x)+2\,{\dfrac {k}{K}}\,\sin(k\,x)\,\cos(k\,x)=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/92e7ca0b7bbc47c72b6d867c25b2946836ff260a)

![{\displaystyle \;\left[\sin(k\,x)+{\dfrac {k}{K}}\,\cos(k\,x)\right]^{\!2}=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b451e0bc4ad8085cbc885c1313a2c6c10d40402)

![{\displaystyle \;\displaystyle \int _{0}^{\mathfrak {a}}\left[\sin(k\,x)+{\dfrac {k}{K}}\,\cos(k\,x)\right]^{2}\,dx=\displaystyle \int _{0}^{\mathfrak {a}}{\dfrac {K^{2}+k^{2}}{2\,K^{2}}}\,dx+\displaystyle \int _{0}^{\mathfrak {a}}{\dfrac {k^{2}-K^{2}}{2\,K^{2}}}\,\cos(2\,k\,x)\,dx+\displaystyle \int _{0}^{\mathfrak {a}}{\dfrac {k}{K}}\,\sin(2\,k\,x)\,dx=\left[{\dfrac {K^{2}+k^{2}}{2\,K^{2}}}\,x+{\dfrac {k^{2}-K^{2}}{2\,K^{2}}}\,{\dfrac {\sin(2\,k\,x)}{2\,k}}+{\dfrac {k}{K}}\,{\dfrac {-\cos(2\,k\,x)}{2\,k}}\right]_{0}^{\mathfrak {a}}\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5fb7127e77d5798ba4871e143a376de8d9dbef34)
![{\displaystyle \;\displaystyle \int _{0}^{\mathfrak {a}}\left[\sin(k\,x)+{\dfrac {k}{K}}\,\cos(k\,x)\right]^{2}\,dx={\dfrac {K^{2}+k^{2}}{2\,K^{2}}}\,{\mathfrak {a}}+{\dfrac {k^{2}-K^{2}}{2\,K^{2}}}\,{\dfrac {\sin(2\,k\,{\mathfrak {a}})}{2\,k}}+{\dfrac {1-\cos(2\,k\,{\mathfrak {a}})}{2\,K}}\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/10ae520d770799b7eafe71cda3102d29a9c1abd4)
![{\displaystyle \;\sin(2\,k\,{\mathfrak {a}})=2\,\sin(k\,{\mathfrak {a}})\,\cos(k\,{\mathfrak {a}})=2\,{\dfrac {2\,\tan \!\left({\dfrac {k\,{\mathfrak {a}}}{2}}\right)\left[1-\tan ^{2}\!\left({\dfrac {k\,{\mathfrak {a}}}{2}}\right)\right]}{\left[1+\tan ^{2}\!\left({\dfrac {k\,{\mathfrak {a}}}{2}}\right)\right]^{2}}}=4\,{\dfrac {{\dfrac {K}{k}}\,\left[1-{\dfrac {K^{2}}{k^{2}}}\right]}{\left[1+{\dfrac {K^{2}}{k^{2}}}\right]^{2}}}=4\,k\,K\,{\dfrac {k^{2}-K^{2}}{\left(k^{2}+K^{2}\right)^{2}}}\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/66003f9c23e54a3f8e772dd051aee201a2ef8417)


![{\displaystyle \;1-\cos(2\,k\,{\mathfrak {a}})=2\,\sin ^{2}(k\,{\mathfrak {a}})=2\,{\dfrac {\left[2\,\tan \!\left({\dfrac {k\,{\mathfrak {a}}}{2}}\right)\right]^{2}}{\left[1+\tan ^{2}\!\left({\dfrac {k\,{\mathfrak {a}}}{2}}\right)\right]^{2}}}=8\,{\dfrac {\dfrac {K^{2}}{k^{2}}}{\left[1+{\dfrac {K^{2}}{k^{2}}}\right]^{2}}}={\dfrac {8\,k^{2}\,K^{2}}{\left(k^{2}+K^{2}\right)^{2}}}\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/267c1f3d6606d381886539dc9a8c4fb7191984c7)


![{\displaystyle \;\sin(2\,k\,{\mathfrak {a}})=2\,{\dfrac {2\,\tan \!\left({\dfrac {k\,{\mathfrak {a}}}{2}}\right)\left[1-\tan ^{2}\!\left({\dfrac {k\,{\mathfrak {a}}}{2}}\right)\right]}{\left[1+\tan ^{2}\!\left({\dfrac {k\,{\mathfrak {a}}}{2}}\right)\right]^{2}}}=4\,{\dfrac {-{\dfrac {k}{K}}\,\left[1-{\dfrac {k^{2}}{K^{2}}}\right]}{\left[1+{\dfrac {k^{2}}{K^{2}}}\right]^{2}}}=4\,k\,K\,{\dfrac {k^{2}-K^{2}}{\left(k^{2}+K^{2}\right)^{2}}}\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/164629b92a836af003073006aebe3503a24298d9)


![{\displaystyle 2\,{\dfrac {\left[2\,\tan \!\left({\dfrac {k\,{\mathfrak {a}}}{2}}\right)\right]^{2}}{\left[1+\tan ^{2}\!\left({\dfrac {k\,{\mathfrak {a}}}{2}}\right)\right]^{2}}}=8\,{\dfrac {\dfrac {k^{2}}{K^{2}}}{\left[1+{\dfrac {k^{2}}{K^{2}}}\right]^{2}}}={\dfrac {8\,k^{2}\,K^{2}}{\left(k^{2}+K^{2}\right)^{2}}}\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/339b8619af80902b26f28050428ba1b21754249e)

![{\displaystyle \;\displaystyle \int _{0}^{\mathfrak {a}}\left[\sin(k\,x)+{\dfrac {k}{K}}\,\cos(k\,x)\right]^{2}\,dx={\dfrac {K^{2}+k^{2}}{2\,K^{2}}}\,{\mathfrak {a}}+{\dfrac {1}{K}}\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9487f2b14f77e1c0aadfb70b43c0e48ca91d53fd)












![{\displaystyle -{\dfrac {K}{k}}\,\left[-{\dfrac {k}{K}}\,\sin(k\,{\mathfrak {a}})+\cos(k\,{\mathfrak {a}})\right]=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32abf9b6f2be7d936a038d3d35210b040752f2fd)
![{\displaystyle -{\dfrac {K}{k}}\,\left[\tan \!\left({\dfrac {k\,{\mathfrak {a}}}{2}}\right)\,\sin(k\,{\mathfrak {a}})+\cos(k\,{\mathfrak {a}})\right]=-{\dfrac {K}{k}}\,{\dfrac {\sin \!\left({\dfrac {k\,{\mathfrak {a}}}{2}}\right)\,\sin(k\,{\mathfrak {a}})+\cos \!\left({\dfrac {k\,{\mathfrak {a}}}{2}}\right)\,\cos(k\,{\mathfrak {a}})}{\cos \!\left({\dfrac {k\,{\mathfrak {a}}}{2}}\right)}}\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e87dc97f1b862be5bd4dfb069e3d902934020fd)




![{\displaystyle \;\Psi (x)=\left\lbrace {\begin{array}{l}\pm {\sqrt {K\,{\dfrac {E}{U_{0}\,\left(1+{\dfrac {K\,{\mathfrak {a}}}{2}}\right)}}}}\,\exp \!\left[-K\,(x-{\mathfrak {a}})\right]\qquad \qquad \quad {\text{ pour }}x\in \left[{\mathfrak {a}},+\infty \right[\\{\sqrt {K\,{\dfrac {U_{0}-E}{U_{0}\,\left(1+{\dfrac {K\,{\mathfrak {a}}}{2}}\right)}}}}\,\left[\sin(k\,x)+{\dfrac {E}{U_{0}-E}}\,\cos(k\,x)\right]{\text{ pour }}x\in \left]0,{\mathfrak {a}}\right[\\{\sqrt {K\,{\dfrac {E}{U_{0}\,\left(1+{\dfrac {K\,{\mathfrak {a}}}{2}}\right)}}}}\,\exp(K\,x)\qquad \qquad \qquad \qquad \quad {\text{ pour }}x\in \left]-\infty ,0\right]\end{array}}\right\rbrace \;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/899dae0435d07975d3fa00dcc77012328763c703)
![{\displaystyle \;\Psi (x)={\sqrt {K\,{\dfrac {E}{U_{0}\,\left(1+{\dfrac {K\,{\mathfrak {a}}}{2}}\right)}}}}\,\left\lbrace {\begin{array}{l}\pm \exp \!\left[-K\,(x-{\mathfrak {a}})\right]\qquad \qquad \qquad \qquad \qquad \quad {\text{ pour }}x\in \left[{\mathfrak {a}},+\infty \right[\\\left[{\sqrt {\dfrac {U_{0}-E}{E}}}\,\sin(k\,x)+{\sqrt {\dfrac {E}{U_{0}-E}}}\,\cos(k\,x)\right]{\text{ pour }}x\in \left]0,{\mathfrak {a}}\right[\\\exp(K\,x)\qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad {\text{ pour }}x\in \left]-\infty ,0\right]\end{array}}\right\rbrace \;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa3e76072173d60537143894e6da727b0aca020e)








![{\displaystyle \;\left]-\infty ,0\right]\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb200fcecf5b106643ef67101845a7b421229e5e)

![{\displaystyle \;\Psi (x)=\pm {\sqrt {K\,{\dfrac {E}{U_{0}\,\left(1+{\dfrac {K\,{\mathfrak {a}}}{2}}\right)}}}}\,\exp \!\left[-K\,(x-{\mathfrak {a}})\right]\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cfb24bb6602e74d566356db67532bf9189186d9e)


































![{\displaystyle \;U(x)=\left\lbrace {\begin{array}{l}U_{0}\rightarrow \;+\infty {\text{ pour }}x\in \left[{\mathfrak {a}}\,,\,+\infty \right[\\0\qquad \qquad \;{\text{ pour }}x\in \left[0\,,\,{\mathfrak {a}}\right]\\U_{0}\rightarrow \;+\infty {\text{ pour }}x\in \left]-\infty \,,\,0\right]\end{array}}\right\rbrace \;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/99e02cdb5110f8693df4fc0e5f4e52d10e218bcb)



![{\displaystyle \;\Psi (x)=\left\lbrace {\begin{array}{l}\gamma \;\exp \!\left(-K\;x\right){\text{ pour }}x\in \left[{\mathfrak {a}}\,,\,+\infty \right[\\\delta \;\exp \!\left(K\;x\right)\;\;\,{\text{ pour }}x\in \left]-\infty \,,\,0\right]\end{array}}\right\rbrace \;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f9b254bb2feb279866a6f9e2c812bb625a3b2a20)






![{\displaystyle \;\Psi (x)=0\;\;{\text{ pour }}x\in \left]-\infty \,,\,0\right[\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a855e96e5c025e1685b09778bb7d3cd63a9c1c2a)


![{\displaystyle \;\Psi (x)=0\;\;{\text{ pour }}x\in \left]{\mathfrak {a}}\,,\,+\infty \right[\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/08f07df50f3d21a832cf5af36bcdc43d45f033a4)






![{\displaystyle \;\Psi (x)=\alpha \,\sin(k\,x)+\beta \,\cos(k\,x){\text{ pour }}x\in \left]0,{\mathfrak {a}}\right[\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/29114b6c9ebf40c412c9e5159023a4b80cf7cb43)

![{\displaystyle \;\color {transparent}{E\in \left]0,U_{0}\right[}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d19a82b6569622a91e3908d1d274062f96634db5)

![{\displaystyle \;\Psi (x)=\alpha \,\sin(k\,x){\text{ pour }}x\in \left]0,{\mathfrak {a}}\right[\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b85d0cd146fb4234c169e254661d36bbd89b6464)




















![{\displaystyle =\left[\Psi _{n}(x)\right]^{2}=\alpha _{n}^{2}\;\sin ^{2}(k_{n}\,x)\;{\text{ pour }}x\in \left[0,{\mathfrak {a}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/15c99c1ef07213182f282586d64e0fbef83668c3)



![{\displaystyle \;\displaystyle \int _{0}^{\mathfrak {a}}\left[1-\cos(2\,k_{n}\,x)\right]\,dx={\dfrac {2}{\alpha _{n}^{2}}}\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/224eadd80b83506a84daad2475feca1377a8c0ab)
![{\displaystyle \;\left[x-{\dfrac {\sin(2\,k_{n}\,x)}{2\,k_{n}}}\right]_{0}^{\mathfrak {a}}={\dfrac {2}{\alpha _{n}^{2}}}\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/247d0f8cbcbea657c7596494a808dc549fa7a971)
![{\displaystyle \;\left[{\mathfrak {a}}-{\cancel {\dfrac {\sin(2\,k_{n}\,{\mathfrak {a}})}{2\,k_{n}}}}\right]={\dfrac {2}{\alpha _{n}^{2}}}\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f7115f434709c2d5e6acf717af73a8d4c7eb3f82)









![{\displaystyle \;\Delta E_{n\,\leftrightarrow \,n+1}=\left[(n+1)^{2}-n^{2}\right]\,{\dfrac {h^{2}}{8\;m\;{\mathfrak {a}}^{2}}}=(2\,n+1)\,{\dfrac {h^{2}}{8\;m\;{\mathfrak {a}}^{2}}}\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/66a8e5b9b49fdcb61ac03f8e693751af3ccaaf15)
































![{\displaystyle \;\left[0\,,\,{\mathfrak {a}}\,\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/16800d32e29ad0f96fc255e86b190b4e6b478114)


![{\displaystyle \;\color {transparent}{\left[0\,,\,{\mathfrak {a}}\,\right]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0967c66a9426b1f848549a619fe2927ef3c4a406)









![{\displaystyle \;\left\langle p_{x}^{2}\right\rangle =(\Delta p_{x})^{2}{\big ]}\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dcf029a7aac84633cf9d9f3b7f48c0ee8e1015aa)







![{\displaystyle \;{\widehat {\mathcal {H}}}\!\left[\,\right]\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ce0c853a9153bd54d4de40dec02ba2d857283f8a)

























![{\displaystyle \;{\mathcal {P}}_{l}(x,\,0)=\vert {\underline {\psi }}(x,\,0)\vert ^{2}=\left[{\underline {\psi }}(x,\,0)\right]\left[{\underline {\psi }}(x,\,0)\right]^{*}\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8396850411016ac55d84def14bfa319857029ce9)
![{\displaystyle \;{\mathcal {P}}_{l}(x,\,0)=\left[{\underline {\alpha }}\;\Psi _{n_{1}}(x)+{\underline {\beta }}\;\Psi _{n_{2}}(x)\right]\left[{\underline {\alpha }}^{*}\;\Psi _{n_{1}}(x)+{\underline {\beta }}^{*}\;\Psi _{n_{2}}(x)\right]=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/684202a5ee466b0e5fce91323d5caf53b996919f)

![{\displaystyle \;{\mathcal {P}}_{l}(x,\,t)=\vert {\underline {\psi }}(x,\,t)\vert ^{2}=\left[{\underline {\psi }}(x,\,t)\right]\left[{\underline {\psi }}(x,\,t)\right]^{*}\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/49c8b5208b6772dc75667d398e1b6b6e45dfb9e3)

![{\displaystyle \left[{\underline {\alpha }}\;\Psi _{n_{1}}(x)\;\exp \!\left(-i\,{\dfrac {E_{n_{1}}}{\hbar }}\,t\right)+{\underline {\beta }}\;\Psi _{n_{2}}(x)\;\exp \!\left(-i\,{\dfrac {E_{n_{2}}}{\hbar }}\,t\right)\right]\left[{\underline {\alpha }}^{*}\;\Psi _{n_{1}}(x)\;\exp \!\left(i\,{\dfrac {E_{n_{1}}}{\hbar }}\,t\right)+{\underline {\beta }}^{*}\;\Psi _{n_{2}}(x)\;\exp \!\left(i\,{\dfrac {E_{n_{2}}}{\hbar }}\,t\right)\right]\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/74a5a096110cd4842066e6b76a35500ed84e51db)




















![{\displaystyle \;\Delta _{t}\left[\;\right]\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1caac2d54d5c5ec76eeba2de40b81145e44d203b)

![{\displaystyle \;\left(\Delta \right)_{t}\left[\;\right]=\left({\dfrac {\partial ^{2}}{\partial x^{2}}}\right)_{\!y,\,z,\,t}\left[\;\right]+\left({\dfrac {\partial ^{2}}{\partial y^{2}}}\right)_{\!x,\,z,\,t}\left[\;\right]+\left({\dfrac {\partial ^{2}}{\partial z^{2}}}\right)_{\!x,\,y,\,t}\left[\;\right]\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93062153efb3942bfd916470d998145cc9a23257)








![{\displaystyle \;x\in \left]-\infty ,0\right]\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd497353c1c386107315f9ee907b808c1de450f5)







![{\displaystyle \;{\mathcal {P}}_{l}(x)=\left[\Psi (x)\right]^{2}=\left[\delta \,\sin(K'\,x)+\delta '\,\cos(K'\,x)\right]^{2}=\delta ^{2}\,\sin ^{2}(K'\,x)+{\delta '}^{2}\,\cos ^{2}(K'\,x)+2\,\delta \,\delta '\,\sin(K'\,x)\,\cos(K'\,x)=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2fdf644c04cc685be19c42e380fb4c955c4953e1)







![{\displaystyle \left[{\dfrac {\delta ^{2}+{\delta '}^{2}}{2}}\,x\right]_{-\infty }^{0}+\left({\delta '}^{2}-\delta ^{2}\right)\left[{\dfrac {\sin(2\,K'\,x)}{4\,K'}}\right]_{-\infty }^{0}-\delta \,\delta '\left[{\dfrac {\cos(2\,K'\,x)}{2\,K'}}\right]_{-\infty }^{0}\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a2728276d596534e7797dc5cdf536a6cde25c38)





![{\displaystyle \;\Psi (x)=\left\lbrace {\begin{array}{l}\gamma \,\exp(-K''\,x)\qquad \qquad \quad \;\;{\text{ pour }}x\in \left[{\mathfrak {a}},+\infty \right[\\\alpha \,\exp(k'\,x)+\beta \,\exp(-k'\,x){\text{ pour }}x\in \left]0,{\mathfrak {a}}\right[\\\delta \,\exp(K''\,x)\qquad \qquad \qquad \;\,{\text{ pour }}x\in \left]-\infty ,0\right]\end{array}}\right\rbrace \;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/45dff8c1874b39a7cad9a9fd282ed233f87597b3)




![{\displaystyle \;\left\lbrace {\begin{array}{c}\Psi ({\mathfrak {a}})\!\!\!&=&\!\!\!\gamma \,\exp(-K''\,{\mathfrak {a}})\!\!\!&=&\!\!\!\alpha \,\exp(k'\,{\mathfrak {a}})+\beta \,\exp(-k'\,{\mathfrak {a}})\\{\dfrac {d\Psi }{dx}}(0)\!\!\!&=&\!\!\!-K''\;\gamma \,\exp(-K''\,{\mathfrak {a}})\!\!\!&=&\!\!\!k'\left[\alpha \,\exp(k'\,{\mathfrak {a}})-\beta \,\exp(-k'\,{\mathfrak {a}})\right]\end{array}}\right\rbrace \;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/80727b38b70ddb7582f7a5f8073ec8ba05c4b460)


![{\displaystyle \;\left\lbrace {\begin{array}{l}\alpha ={\dfrac {\gamma \,\exp \!\left[-(K''+k')\,{\mathfrak {a}}\right]}{2}}\;\left(1-{\dfrac {K''}{k'}}\right)\\\beta ={\dfrac {\gamma \,\exp \!\left[-(K''-k')\,{\mathfrak {a}}\right]}{2}}\;\left(1+{\dfrac {K''}{k'}}\right)\end{array}}\right\rbrace }](https://wikimedia.org/api/rest_v1/media/math/render/svg/46ec07dee8962ff4b9402a7f270e51335f8d865f)

![{\displaystyle \;\alpha ={\dfrac {\delta }{2}}\left(1+{\dfrac {K''}{k'}}\right)={\dfrac {\gamma \,\exp \!\left[-(K''+k')\,{\mathfrak {a}}\right]}{2}}\;\left(1-{\dfrac {K''}{k'}}\right)\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/04b089acac19fb218ec92d76922fb1eac425ed77)

![{\displaystyle \gamma \,\exp \!\left[-(K''+k')\,{\mathfrak {a}}\right]\;{\dfrac {1-{\dfrac {K''}{k'}}}{1+{\dfrac {K''}{k'}}}}\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e9175393b795ed3aea66f80135b9ddef99be124e)
![{\displaystyle \;\beta ={\dfrac {\delta }{2}}\left(1-{\dfrac {K''}{k'}}\right)={\dfrac {\gamma \,\exp \!\left[-(K''-k')\,{\mathfrak {a}}\right]}{2}}\;\left(1+{\dfrac {K''}{k'}}\right)\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/10ba5aba11cd0cdf0a7046f981428648704bfc0e)
![{\displaystyle \gamma \,\exp \!\left[-(K''-k')\,{\mathfrak {a}}\right]\;{\dfrac {1+{\dfrac {K''}{k'}}}{1-{\dfrac {K''}{k'}}}}\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3135ba99a5856609d8fc77e26aaba6ee4afae5ff)

![{\displaystyle \;\exp \!\left[-(K''+k')\,{\mathfrak {a}}\right]\;{\dfrac {1-{\dfrac {K''}{k'}}}{1+{\dfrac {K''}{k'}}}}\;{\overset {?}{=}}\;\exp \!\left[-(K''-k')\,{\mathfrak {a}}\right]\;{\dfrac {1+{\dfrac {K''}{k'}}}{1-{\dfrac {K''}{k'}}}}\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a8dc820ed93d505545201dfd569385b1e9553b2)

![{\displaystyle \left[{\dfrac {1+{\dfrac {K''}{k'}}}{1-{\dfrac {K''}{k'}}}}\right]^{2}\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7285754314c7c85b3ca67cbf31dbd19df92116a8)























![{\displaystyle \;\left]-\infty \,;\,0\right]\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/85e9a8f44caef43704e458410787f4605ef5fffe)

![{\displaystyle \;x\in \left]-\infty \,,\,0\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e051a266f14e1750d6a11f078c36fd93716eccbf)





































![{\displaystyle \;{\underline {\alpha }}\,{\underline {\beta }}^{*}+{\underline {\alpha }}^{*}\,{\underline {\beta }}=\vert {\underline {\alpha }}\vert \,\vert {\underline {\beta }}\vert \left\lbrace \exp \!\left[i\,(\varphi _{\alpha }-\varphi _{\beta })\right]+\exp \!\left[-i\,(\varphi _{\alpha }-\varphi _{\beta })\right]\right\rbrace =\vert {\underline {\alpha }}\vert \,\vert {\underline {\beta }}\vert \;2\,\cos \!\left(\varphi _{\alpha }-\varphi _{\beta }\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6ec0c7ac5f075ae3f2f87cfd96d1e93ce16f0133)

![{\displaystyle \vert {\underline {\alpha }}\vert \,\vert {\underline {\beta }}\vert \left\lbrace \exp \!\left[i\,\left({\dfrac {E_{n_{2}}-E_{n_{1}}}{\hbar }}\,t+\varphi _{\alpha }-\varphi _{\beta }\right)\right]+\exp \!\left[-i\,\left({\dfrac {E_{n_{2}}-E_{n_{1}}}{\hbar }}\,t+\varphi _{\alpha }-\varphi _{\beta }\right)\right]\right\rbrace =}](https://wikimedia.org/api/rest_v1/media/math/render/svg/726547ad883d3e5c5e882ceb82cf1235ec526c62)





![{\displaystyle \;E\in \left[\min {\big (}E_{n_{1}}\,,\,E_{n_{2}}{\big )}\;,\,\max {\big (}E_{n_{1}}\,,\,E_{n_{2}}{\big )}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5cd524ff8146ad4cabe3792f1860669843b8c1a7)