Utilisateur:Ellande/Brouillon2

Ellande

Outils

Discussion

Brouillon 1

Brouillon 2

Brouillon 3

Brouillon 4

Brouillon 5

Brouillon 6

Brouillon 7

Brouillon 8

Brouillon 9

Bac à sable

Intégrale simple

Rappel sur l'intégrale de Riemann

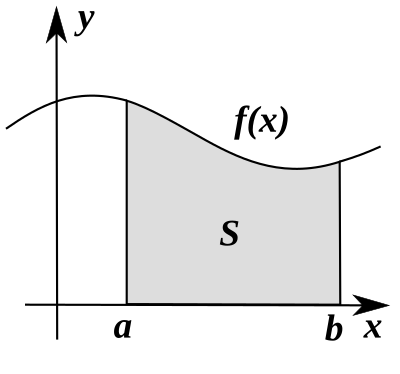
Le calcul d'intégrales au sens de Riemann correspond au calcul de l'aire comprise entre l'axe des abscisses et la courbe d'une fonction f donnée entre deux bornes a et b. Sa définition repose sur une suite de fonctions en escaliers convergeant vers f sur le segment [a,b]. En d'autres termes :

Définition - Intégrale de Riemann

Soit f une fonction continue définie sur le segment [a,b]. On définit l'intégrale de a à b de la fonction f par $\int _{a}^{b}f(x)\mathrm {d} x=\lim _{n\rightarrow +\infty }{\frac {b-a}{n}}\sum _{k=0}^{n-1}f\left(a+{\frac {b-a}{n}}k\right)$

Grossièrement, cela revient à :

« découper » le segment [a,b] en petits morceaux
à construire des rectangles s'appuyant sur chaque portion de segment ainsi que sur la courbe de f
à approcher l'intégrale de f par la somme des aires des rectangles.

Cette « approximation » est d'autant meilleure que le nombre de divisions du segment [a,b] augmente.

Notation

En physique, il arrive très couramment de considérer les différentielles des grandeurs comme des petites variations de ces grandeurs. C'est ce que l’on retrouve dans la notation différentielle de la dérivation, par exemple dans l'équation différentielle d'un circuit RLC :

{\frac {\mathrm {d} ^{2}u_{C}}{\mathrm {d} t^{2}}}+{\frac {R+r}{L}}{\frac {\mathrm {d} u_{C}}{\mathrm {d} t}}+{\frac {1}{LC}}u_{c}=0

du_C est une petite variation de la tension aux bornes du condensateur, et dt la petite variation de temps pendant laquelle la variation du_C a eu lieu. Lorsque ces grandeurs deviennent infiniment petites, on retrouve bien le nombre dérivé de u_C à l'instant t étudié. du_C et dt sont des infiniment petits d'ordre 1.

La notation de l'intégrale reprend l’idée de la somme de Riemann tout en incluant cette notion d'infiniments petit. À l'origine, le symbole intégrale $\scriptstyle \int$ était un S utilisé par Leibniz pour écrire des sommes. Calculer l'intégrale d'une fonction f sur un segment [a,b], c’est comme faire la somme d'une infinité de rectangles infiniments fins, de largeur dx et de hauteur f(x) pour « tous les x entre a et b ».

Intuitivement, cette opération permet bien d'obtenir l'aire totale comprise entre la courbe de f et l'axe des abscisses.

${\mathcal {A}}=\int _{a}^{b}f(x)\mathrm {d} x$

f(x) dx est l'aire du « rectangle infinitésimal courant »
Le symbole $\scriptstyle \int _{a}^{b}$ indique qu'on somme les rectangles infinitésimaux entre a et b

Passage du discret au continu

C'est ainsi qu'en physique on utilise les intégrales pour sommer les contributions d'éléments que l’on ne peut pas compter car leur distribution est continue (le long d'une ligne, sur un plan ou une nappe, ou même dans un volume) et non discrète (ensemble de points indénombrable).

Des exemples valent parfois mieux qu'un long discours.

Exemple tiré de l'électrostatique

Notions d'électrostatique

* Soient deux particules immobiles chargées A et B, de charges respectives q_A et q_B. La force électrostatique exercée par A sur B vaut

{\vec {F}}_{A\rightarrow B}={\frac {q_{A}q_{B}}{4\pi \varepsilon _{0}{\rm {AB}}^{2}}}{\vec {u}}_{AB}

.

Soit une particule A immobile dans l'espace, de charge q_A. Le champ électrostatique généré par A en M, noté ${\vec {E}}_{A}(M)$ , est défini par ${\vec {E}}_{A}(M)={\frac {q_{A}}{4\pi \varepsilon _{0}r^{2}}}{\vec {u}}_{r}$ où r=AM.
Soit une particule B de charge $q_{B}$ placée dans le champ généré par A. Alors B est soumise à la force ${\vec {F}}_{A\rightarrow B}={\frac {q_{A}q_{B}}{4\pi \varepsilon _{0}r^{2}}}{\vec {u}}_{r}=q_{B}{\vec {E}}_{A}(B)$ où r=AB.

Théorème de superposition

Soient n particules A₁, A₂, ..., A_n, immobiles dans l'espace, de charges respectives q₁, q₂, ... q_n.

Le champ électrostatique généré par cette distribution est la somme des champs engendrés par chacune des particules : ${\vec {E}}(M)={\vec {E}}_{A_{1}}(M)+{\vec {E}}_{A_{2}}(M)+\cdots +{\vec {E}}_{A_{n}}(M)$ .

Une particule de charge q placée en M est alors soumise à une force ${\vec {F}}=q{\vec {E}}(M)$ .

On dispose alors de n charges ponctuelles de l'espace, c'est-à-dire une répartition discrète. On peut sommer comme on a l'habitude de faire les contributions de chaque charge.

Les choses se gâtent lorsqu'on se trouve face à une distribution continue de charges, par exemple lorsqu'on est en présence d'une ligne de charges Г.

On suppose que cette distribution admet une densité linéique de charge λ. Cela signifie qu'en un point M de la distribution, une longueur infinitésimale dL de la distribution porte une charge électrique $\mathrm {d} q(M)=\lambda (M)~\mathrm {d} L$ .

Pour trouver le champ électrostatique généré par la distribution en P, il faudrait sommer les contibutions de chaque élément infinitésimal de la distribution. Un élément de longueur dL en un point M de Γ porte une charge $\mathrm {d} q(M)=\lambda (M)~\mathrm {d} L$ , donc engendre par définition en P un champ électrique élémentaire $\mathrm {d} {\vec {E}}(P)={\frac {\mathrm {d} q(M){\vec {u}}_{\rm {MP}}}{4\pi \varepsilon _{0}\,{\rm {MP}}^{2}}}$

Il ne reste plus qu’à sommer sur toute la longueur de Γ en intégrant sur Γ, c'est-à-dire en sommant les contributions de tous les points M :

${\vec {E}}(P)=\int _{\Gamma }{\frac {\mathrm {d} q(M){\vec {u}}_{r}}{4\pi \varepsilon _{0}\,{\rm {MP}}^{2}}}=\int _{\Gamma }{\frac {\lambda (M){\vec {u}}_{r}}{4\pi \varepsilon _{0}\,{\rm {MP}}^{2}}}\mathrm {d} L$ avec ${\vec {u}}_{r}$ vecteur unitaire de même sens et même direction que ${\overrightarrow {\rm {MP}}}$

Voir la ressemblance avec l’expression discrète ${\vec {E}}(P)=\sum _{i=1}^{n}{\frac {q_{i}}{4\pi \varepsilon _{0}\,{\rm {M_{i}P}}^{2}}}{\vec {u}}_{\rm {M_{i}P}}$