En raison de limitations techniques, la typographie souhaitable du titre, «
Exercices : Courbes et surfaces dans ℝ3 », n'a pu être restituée correctement ci-dessus.
En raison de limitations techniques, la typographie souhaitable du titre, «
Exercice : Courbes et surfaces dans R3Calcul différentiel/Exercices/Courbes et surfaces dans R3 », n'a pu être restituée correctement ci-dessus.
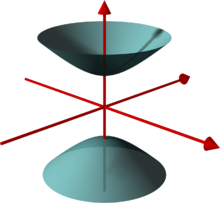
Calculer l'équation du plan tangent au cône à base elliptique
Σ
{\displaystyle \Sigma }
x
y
=
z
2
{\displaystyle xy=z^{2}}
M
0
=
(
x
0
,
y
0
,
z
0
)
≠
(
0
,
0
,
0
)
{\displaystyle M_{0}=(x_{0},y_{0},z_{0})\neq (0,0,0)}
Σ
{\displaystyle \Sigma }
Solution
Σ
{\displaystyle \Sigma }
f
=
0
{\displaystyle f=0}
f
{\displaystyle f}
f
(
x
,
y
,
z
)
=
x
y
−
z
2
{\displaystyle f\left(x,y,z\right)=xy-z^{2}}
Le plan tangent
T
M
0
Σ
{\displaystyle T_{M_{0}}\Sigma }
M
0
{\displaystyle M_{0}}
∇
f
(
x
0
,
y
0
,
z
0
)
=
(
y
0
,
x
0
,
−
2
z
0
)
{\displaystyle \nabla f\left(x_{0},y_{0},z_{0}\right)=\left(y_{0},x_{0},-2z_{0}\right)}
Il a donc pour équation
(
x
−
x
0
)
y
0
+
(
y
−
y
0
)
x
0
−
2
(
z
−
z
0
)
z
0
=
0
{\displaystyle (x-x_{0})y_{0}+(y-y_{0})x_{0}-2(z-z_{0})z_{0}=0}
y
0
x
+
x
0
y
−
2
z
0
z
=
0
{\displaystyle y_{0}x+x_{0}y-2z_{0}z=0}
Déterminer les points de la surface
S
{\displaystyle S}
x
y
=
z
3
{\displaystyle xy=z^{3}}
x
=
2
,
y
−
3
z
+
3
=
0
{\displaystyle x=2,\;y-3z+3=0}
En tout point
M
0
=
(
x
0
,
y
0
,
z
0
)
∈
S
{\displaystyle M_{0}=\left(x_{0},y_{0},z_{0}\right)\in S}
x
0
y
0
≠
0
{\displaystyle x_{0}y_{0}\neq 0}
Solution
S
{\displaystyle S}
f
=
0
{\displaystyle f=0}
f
{\displaystyle f}
f
(
x
,
y
,
z
)
=
x
y
−
z
3
{\displaystyle f\left(x,y,z\right)=xy-z^{3}}
Pour tout point
M
0
=
(
x
0
,
y
0
,
z
0
)
∈
S
{\displaystyle M_{0}=\left(x_{0},y_{0},z_{0}\right)\in S}
T
M
0
S
{\displaystyle T_{M_{0}}S}
M
0
{\displaystyle M_{0}}
∇
f
(
x
0
,
y
0
,
z
0
)
=
(
y
0
,
x
0
,
−
3
z
0
2
)
{\displaystyle \nabla f\left(x_{0},y_{0},z_{0}\right)=\left(y_{0},x_{0},-3z_{0}^{2}\right)}
O
=
(
0
,
0
,
0
)
{\displaystyle O=\left(0,0,0\right)}
y
0
(
x
−
x
0
)
+
x
0
(
y
−
y
0
)
−
3
z
0
2
(
z
−
z
0
)
=
0
{\displaystyle y_{0}\left(x-x_{0}\right)+x_{0}\left(y-y_{0}\right)-3z_{0}^{2}\left(z-z_{0}\right)=0}
y
0
x
+
x
0
y
−
3
z
0
2
z
=
2
x
0
y
0
−
3
z
0
3
{\displaystyle y_{0}x+x_{0}y-3z_{0}^{2}z=2x_{0}y_{0}-3z_{0}^{3}}
T
M
0
S
=
{
(
x
,
y
,
z
)
∈
R
3
∣
y
0
x
+
x
0
y
−
3
z
0
2
z
=
−
z
0
3
}
{\displaystyle T_{M_{0}}S=\{\left(x,y,z\right)\in \mathbb {R} ^{3}\mid y_{0}x+x_{0}y-3z_{0}^{2}z=-z_{0}^{3}\}}
D
{\displaystyle D}
z
{\displaystyle z}
D
=
{
(
2
,
3
z
−
3
,
z
)
∣
z
∈
R
}
{\displaystyle D=\{\left(2,3z-3,z\right)\mid z\in \mathbb {R} \}}
D
⊂
T
M
0
S
⇔
∀
z
∈
R
2
y
0
+
x
0
(
3
z
−
3
)
−
3
z
0
2
z
=
−
z
0
3
⇔
∀
z
∈
R
z
(
3
x
0
−
3
z
0
2
)
+
(
2
y
0
−
3
x
0
+
z
0
3
)
=
0
⇔
x
0
=
z
0
2
et
2
y
0
−
3
x
0
+
z
0
3
=
0
⇔
x
0
=
z
0
2
et
y
0
=
z
0
2
3
−
z
0
2
.
{\displaystyle {\begin{aligned}D\subset T_{M_{0}}S&\Leftrightarrow \forall z\in \mathbb {R} \quad 2y_{0}+x_{0}\left(3z-3\right)-3z_{0}^{2}z=-z_{0}^{3}\\&\Leftrightarrow \forall z\in \mathbb {R} \quad z\left(3x_{0}-3z_{0}^{2}\right)+\left(2y_{0}-3x_{0}+z_{0}^{3}\right)=0\\&\Leftrightarrow x_{0}=z_{0}^{2}\quad {\text{et}}\quad 2y_{0}-3x_{0}+z_{0}^{3}=0\\&\Leftrightarrow x_{0}=z_{0}^{2}{\text{ et }}y_{0}=z_{0}^{2}{\frac {3-z_{0}}{2}}.\end{aligned}}}
0
=
x
0
y
0
−
z
0
3
=
z
0
4
3
−
z
0
2
−
z
0
3
=
z
0
3
2
(
3
z
0
−
z
0
2
−
2
)
=
−
z
0
3
2
(
z
0
−
1
)
(
z
0
−
2
)
{\displaystyle 0=x_{0}y_{0}-z_{0}^{3}=z_{0}^{4}{\frac {3-z_{0}}{2}}-z_{0}^{3}={\frac {z_{0}^{3}}{2}}\left(3z_{0}-z_{0}^{2}-2\right)=-{\frac {z_{0}^{3}}{2}}\left(z_{0}-1\right)\left(z_{0}-2\right)}
M
0
≠
O
{\displaystyle M_{0}\neq O}
M
0
=
(
1
,
1
,
1
)
ou
(
4
,
2
,
2
)
{\displaystyle M_{0}=\left(1,1,1\right)\quad {\text{ou}}\quad \left(4,2,2\right)}
Calculons le développement limité à l'ordre
2
{\displaystyle 2}
z
=
x
y
3
{\displaystyle z={\sqrt[{3}]{xy}}}
x
=
x
0
+
u
{\displaystyle x=x_{0}+u}
y
=
y
0
+
v
{\displaystyle y=y_{0}+v}
u
,
v
→
0
{\displaystyle u,v\to 0}
z
0
=
x
0
y
0
3
{\displaystyle z_{0}={\sqrt[{3}]{x_{0}y_{0}}}}
(
x
0
+
u
)
(
y
0
+
v
)
3
=
z
0
(
1
+
u
x
0
)
1
/
3
(
1
+
v
y
0
)
1
/
3
=
z
0
(
1
+
u
3
x
0
−
u
2
9
x
0
2
)
(
1
+
v
3
y
0
−
v
2
9
y
0
2
)
+
o
(
u
2
+
v
2
)
=
z
0
+
z
0
3
x
0
u
+
z
0
3
y
0
v
+
z
0
9
(
−
u
2
x
0
2
+
u
v
x
0
y
0
−
v
2
y
0
2
)
+
o
(
u
2
+
v
2
)
.
{\displaystyle {\begin{aligned}{\sqrt[{3}]{\left(x_{0}+u\right)\left(y_{0}+v\right)}}&=z_{0}\left(1+{\frac {u}{x_{0}}}\right)^{1/3}\left(1+{\frac {v}{y_{0}}}\right)^{1/3}\\&=z_{0}\left(1+{\frac {u}{3x_{0}}}-{\frac {u^{2}}{9x_{0}^{2}}}\right)\left(1+{\frac {v}{3y_{0}}}-{\frac {v^{2}}{9y_{0}^{2}}}\right)+o\left(u^{2}+v^{2}\right)\\&=z_{0}+{\frac {z_{0}}{3x_{0}}}u+{\frac {z_{0}}{3y_{0}}}v+{\frac {z_{0}}{9}}\left(-{\frac {u^{2}}{x_{0}^{2}}}+{\frac {uv}{x_{0}y_{0}}}-{\frac {v^{2}}{y_{0}^{2}}}\right)+o\left(u^{2}+v^{2}\right).\end{aligned}}}
z
=
z
0
+
z
0
3
x
0
u
+
z
0
3
y
0
v
=
z
0
+
y
0
u
+
x
0
v
3
z
0
2
{\displaystyle z=z_{0}+{\frac {z_{0}}{3x_{0}}}u+{\frac {z_{0}}{3y_{0}}}v=z_{0}+{\frac {y_{0}u+x_{0}v}{3z_{0}^{2}}}}
−
z
0
{\displaystyle -z_{0}}
x
0
y
0
>
0
{\displaystyle x_{0}y_{0}>0}
x
0
y
0
<
0
{\displaystyle x_{0}y_{0}<0}
Pour
λ
∈
R
{\displaystyle \lambda \in \mathbb {R} }
S
λ
=
{
(
x
1
,
x
2
,
x
3
)
∈
R
3
∣
x
1
2
+
x
2
2
−
x
3
2
=
λ
}
{\displaystyle S_{\lambda }=\{(x_{1},x_{2},x_{3})\in \mathbb {R} ^{3}\mid x_{1}^{2}+x_{2}^{2}-x_{3}^{2}=\lambda \}}
Déterminer les réels
λ
{\displaystyle \lambda }
S
λ
{\displaystyle S_{\lambda }}
sous-variété de
R
3
{\displaystyle \mathbb {R} ^{3}}
S
λ
{\displaystyle S_{\lambda }}
λ
{\displaystyle \lambda }
Pour
x
,
y
∈
R
3
{\displaystyle x,y\in \mathbb {R} ^{3}}
B
(
x
,
y
)
=
x
1
y
1
+
x
2
y
2
−
x
3
y
3
{\displaystyle B(x,y)=x_{1}y_{1}+x_{2}y_{2}-x_{3}y_{3}}
x
∈
S
λ
{\displaystyle x\in S_{\lambda }}
T
x
S
λ
{\displaystyle \mathrm {T} _{x}S_{\lambda }}
B
{\displaystyle B}
Solution
Hyperboloïde à une nappe (
λ
>
0
{\displaystyle \lambda >0}
Hyperboloïde à deux nappes (
λ
>
0
{\displaystyle \lambda >0}
S
λ
{\displaystyle S_{\lambda }}
f
:
R
3
→
R
,
x
↦
x
1
2
+
x
2
2
−
x
3
2
{\displaystyle f:\mathbb {R} ^{3}\to \mathbb {R} ,\,x\mapsto x_{1}^{2}+x_{2}^{2}-x_{3}^{2}}
submersion , c'est-à-dire si, pour tout
x
∈
S
λ
{\displaystyle x\in S_{\lambda }}
∇
f
(
x
)
=
(
2
x
1
,
2
x
2
,
−
2
x
3
)
{\displaystyle \nabla f(x)=(2x_{1},2x_{2},-2x_{3})}
(
0
,
0
,
0
)
∉
S
λ
{\displaystyle (0,0,0)\notin S_{\lambda }}
λ
≠
0
{\displaystyle \lambda \neq 0}
S
λ
{\displaystyle S_{\lambda }}
surface de révolution , d'axe
(
O
x
3
)
{\displaystyle (Ox_{3})}
cône si
λ
=
0
{\displaystyle \lambda =0}
à une nappe si
λ
>
0
{\displaystyle \lambda >0}
deux nappes si
λ
<
0
{\displaystyle \lambda <0}
T
x
S
λ
=
ker
d
f
x
=
∇
f
(
x
)
⊥
=
ker
B
(
x
,
⋅
)
{\displaystyle T_{x}S_{\lambda }=\ker \mathrm {d} f_{x}=\nabla f(x)^{\bot }=\ker B(x,\cdot )}
Déterminer, parmi les sous-ensembles ci-dessous, lesquels sont des sous-variétés de
R
n
{\displaystyle \mathbb {R} ^{n}}
S
0
=
{
(
x
,
y
,
z
)
∈
R
3
∣
x
3
+
y
3
+
z
3
−
3
x
y
z
=
1
}
{\displaystyle S_{0}=\{(x,y,z)\in \mathbb {R} ^{3}\mid x^{3}+y^{3}+z^{3}-3xyz=1\}}
C
0
=
{
(
x
,
y
)
∈
R
2
∣
x
y
=
0
}
{\displaystyle C_{0}=\{(x,y)\in \mathbb {R} ^{2}\mid xy=0\}}
C
1
=
{
(
x
,
y
,
z
)
∈
R
3
∣
x
2
+
y
2
+
z
2
=
1
et
x
2
+
y
2
−
x
=
0
}
{\displaystyle C_{1}=\{(x,y,z)\in \mathbb {R} ^{3}\mid x^{2}+y^{2}+z^{2}=1\;{\text{et}}\;x^{2}+y^{2}-x=0\}}
C
2
=
{
(
x
,
y
)
∈
R
2
∣
y
2
=
x
3
}
{\displaystyle C_{2}=\{(x,y)\in \mathbb {R} ^{2}\mid y^{2}=x^{3}\}}
S
1
=
{
(
x
,
y
,
z
)
∈
R
3
∣
x
2
+
y
2
=
α
z
2
}
{\displaystyle S_{1}=\{(x,y,z)\in \mathbb {R} ^{3}\mid x^{2}+y^{2}=\alpha z^{2}\}}
α
>
0
{\displaystyle \alpha >0}
Solution
La surface
S
0
{\displaystyle S_{0}}
R
3
{\displaystyle \mathbb {R} ^{3}}
f
:
R
3
→
R
,
(
x
,
y
,
z
)
↦
x
3
+
y
3
+
z
3
−
3
x
y
z
{\displaystyle f:\mathbb {R} ^{3}\to \mathbb {R} ,\,(x,y,z)\mapsto x^{3}+y^{3}+z^{3}-3xyz}
(
x
,
y
,
z
)
∈
S
0
{\displaystyle (x,y,z)\in S_{0}}
∇
f
(
x
,
y
,
z
)
=
3
(
x
2
−
y
z
,
y
2
−
x
z
,
z
2
−
x
y
)
{\displaystyle \nabla f(x,y,z)=3(x^{2}-yz,y^{2}-xz,z^{2}-xy)}
(
x
,
y
,
z
)
{\displaystyle (x,y,z)}
f
(
x
,
y
,
z
)
=
0
{\displaystyle f(x,y,z)=0}
La courbe
C
0
{\displaystyle C_{0}}
R
2
{\displaystyle \mathbb {R} ^{2}}
O
{\displaystyle O}
C
0
{\displaystyle C_{0}}
O
{\displaystyle O}
La courbe
C
1
{\displaystyle C_{1}}
fenêtre de Viviani ») a pour paramétrage
M
(
θ
)
=
(
cos
2
θ
,
cos
θ
sin
θ
,
sin
θ
)
{\displaystyle M(\theta )=(\cos ^{2}\theta ,\cos \theta \sin \theta ,\sin \theta )}
M
(
0
)
=
(
1
,
0
,
0
)
=
M
(
π
)
{\displaystyle M(0)=(1,0,0)=M(\pi )}
C
0
{\displaystyle C_{0}}
C
1
{\displaystyle C_{1}}
La courbe
C
2
=
{
(
y
2
3
,
y
)
∣
y
∈
R
}
{\displaystyle C_{2}=\{({\sqrt[{3}]{y^{2}}},y)\mid y\in \mathbb {R} \}}
R
×
{
0
}
{\displaystyle \mathbb {R} \times \{0\}}
R
2
{\displaystyle \mathbb {R} ^{2}}
O
=
(
0
,
0
)
{\displaystyle O=(0,0)}
lim
O
M
n
→
t
n
{\displaystyle \lim {\frac {\overrightarrow {OM_{n}}}{t_{n}}}}
M
n
→
O
{\displaystyle M_{n}\to O}
t
n
→
0
+
{\displaystyle t_{n}\to 0^{+}}
γ
d
′
(
0
)
=
lim
t
→
0
+
γ
(
t
)
−
γ
(
0
)
t
{\displaystyle \gamma '_{d}(0)=\lim _{t\to 0^{+}}{\frac {\gamma (t)-\gamma (0)}{t}}}
γ
:
[
0
,
ε
[
→
C
2
{\displaystyle \gamma :\left[0,\varepsilon \right[\to C_{2}}
γ
(
0
)
=
O
{\displaystyle \gamma (0)=O}
Le cône
S
1
{\displaystyle S_{1}}
R
3
{\displaystyle \mathbb {R} ^{3}}
O
{\displaystyle O}
O
{\displaystyle O}
S
1
{\displaystyle S_{1}}
O
{\displaystyle O}
On considère la sphère unité
S
{\displaystyle S}
R
3
{\displaystyle \mathbb {R} ^{3}}
C
{\displaystyle C}
r
>
0
{\displaystyle r>0}
S
{\displaystyle S}
C
{\displaystyle C}
Solution
Sans perte de généralité, l'axe du cylindre passe par un point de la forme
(
a
,
0
,
0
)
{\displaystyle (a,0,0)}
a
≥
0
{\displaystyle a\geq 0}
La courbe
S
∩
C
{\displaystyle S\cap C}
f
:
R
3
→
R
2
,
(
x
,
y
,
z
)
↦
(
x
2
+
y
2
+
z
2
−
1
,
(
x
−
a
)
2
+
y
2
−
r
2
)
{\displaystyle f:\mathbb {R} ^{3}\to \mathbb {R} ^{2},\ (x,y,z)\mapsto (x^{2}+y^{2}+z^{2}-1,(x-a)^{2}+y^{2}-r^{2})}
La matrice
J
f
(
x
,
y
,
z
)
=
2
(
x
y
z
x
−
a
y
0
)
{\displaystyle \mathrm {J} f(x,y,z)=2{\begin{pmatrix}x&y&z\\x-a&y&0\end{pmatrix}}}
y
z
=
(
x
−
a
)
z
=
a
y
=
0
{\displaystyle yz=(x-a)z=ay=0}
Si
a
=
0
{\displaystyle a=0}
S
∩
C
{\displaystyle S\cap C}
r
=
1
{\displaystyle r=1}
S
∩
C
{\displaystyle S\cap C}
S
{\displaystyle S}
Si
a
≠
0
{\displaystyle a\neq 0}
S
∩
C
{\displaystyle S\cap C}
r
∈
{
1
+
a
,
1
−
a
,
a
−
1
}
{\displaystyle r\in \{1+a,1-a,a-1\}}
Si
r
=
a
+
1
{\displaystyle r=a+1}
Si
r
=
a
−
1
{\displaystyle r=a-1}
Si
r
=
1
−
a
{\displaystyle r=1-a}
S
∩
C
{\displaystyle S\cap C}
a
=
r
=
1
2
{\displaystyle a=r={\frac {1}{2}}}
Montrer que l'équation
x
y
+
x
z
+
y
z
+
2
x
+
2
y
−
z
=
0
{\displaystyle xy+xz+yz+2x+2y-z=0}
S
{\displaystyle S}
Montrer que le système d'équations
4
x
y
+
2
x
z
+
4
y
−
z
=
x
y
+
x
z
+
y
z
+
2
x
+
2
y
−
z
=
0
{\displaystyle 4xy+2xz+4y-z=xy+xz+yz+2x+2y-z=0}
Montrer que le système d'équations
x
2
+
y
2
−
z
2
=
2
x
+
y
+
1
=
0
{\displaystyle x^{2}+y^{2}-z^{2}=2x+y+1=0}
C
{\displaystyle C}
R
3
{\displaystyle \mathbb {R} ^{3}}
T
a
C
{\displaystyle T_{a}C}
C
{\displaystyle C}
a
=
(
−
1
,
1
,
2
)
{\displaystyle a=(-1,1,{\sqrt {2}})}
Solution
Posons
f
:
(
x
,
y
,
z
)
↦
x
y
+
x
z
+
y
z
+
2
x
+
2
y
−
z
{\displaystyle f:(x,y,z)\mapsto xy+xz+yz+2x+2y-z}
J
f
=
(
y
+
z
+
2
,
x
+
z
+
2
,
x
+
y
−
1
)
{\displaystyle \mathrm {J} f=(y+z+2,x+z+2,x+y-1)}
(
1
/
2
,
1
/
2
,
−
5
/
2
)
{\displaystyle (1/2,1/2,-5/2)}
f
≠
0
{\displaystyle f\neq 0}
S
{\displaystyle S}
R
3
{\displaystyle \mathbb {R} ^{3}}
(
0
,
0
,
0
)
{\displaystyle (0,0,0)}
ker
(
D
f
(
0
,
0
,
0
)
)
{\displaystyle \ker(\mathrm {D} f_{(0,0,0)})}
2
x
+
2
y
−
z
=
0
{\displaystyle 2x+2y-z=0}
Posons
g
:
(
x
,
y
,
z
)
↦
(
4
x
y
+
2
x
z
+
4
y
−
z
,
x
y
+
x
z
+
y
z
+
2
x
+
2
y
−
z
)
{\displaystyle g:(x,y,z)\mapsto (4xy+2xz+4y-z,xy+xz+yz+2x+2y-z)}
J
g
(
0
,
0
,
0
)
=
(
0
4
−
1
2
2
−
1
)
{\displaystyle \mathrm {J} g(0,0,0)={\begin{pmatrix}0&4&-1\\2&2&-1\end{pmatrix}}}
(
1
,
1
,
4
)
{\displaystyle (1,1,4)}
L'application
F
:
R
3
→
R
2
,
(
x
,
y
,
z
)
↦
(
x
2
+
y
2
−
z
2
,
2
x
+
y
+
1
)
{\displaystyle F:\mathbb {R} ^{3}\to \mathbb {R} ^{2},\;(x,y,z)\mapsto (x^{2}+y^{2}-z^{2},2x+y+1)}
∞ . Soit
(
x
,
y
,
z
)
∈
C
{\displaystyle (x,y,z)\in C}
z
≠
0
{\displaystyle z\neq 0}
J
(
x
,
y
,
z
)
F
=
(
2
x
2
y
−
2
z
2
1
0
)
{\displaystyle J_{(x,y,z)}F=\left({\begin{smallmatrix}2x&2y&-2z\\2&1&0\end{smallmatrix}}\right)}
F
{\displaystyle F}
C
{\displaystyle C}
C
{\displaystyle C}
R
3
{\displaystyle \mathbb {R} ^{3}}
3
−
2
=
1
{\displaystyle 3-2=1}
F
(
a
)
=
0
{\displaystyle F(a)=0}
a
∈
C
{\displaystyle a\in C}
T
a
C
=
ker
D
a
F
{\displaystyle T_{a}C=\ker \mathrm {D} _{a}F}
(
α
,
β
,
γ
)
∈
R
3
{\displaystyle (\alpha ,\beta ,\gamma )\in \mathbb {R} ^{3}}
−
2
α
+
2
β
−
2
2
γ
=
2
α
+
β
=
0
{\displaystyle -2\alpha +2\beta -2{\sqrt {2}}\gamma =2\alpha +\beta =0}
On appelle groupe orthogonal l'ensemble
O
n
(
R
)
=
{
M
∈
M
n
(
R
)
∣
t
M
M
=
I
n
}
{\displaystyle \mathrm {O} _{n}(\mathbb {R} )=\{M\in \mathrm {M} _{n}(\mathbb {R} )\mid {}^{t}\!MM=\mathrm {I} _{n}\}}
Le but est de montrer que
O
n
(
R
)
{\displaystyle \mathrm {O} _{n}(\mathbb {R} )}
M
n
(
R
)
{\displaystyle \mathrm {M} _{n}(\mathbb {R} )}
Soit
E
{\displaystyle E}
n
{\displaystyle n}
f
:
M
n
(
R
)
→
E
{\displaystyle f:\mathrm {M} _{n}(\mathbb {R} )\to E}
f
(
A
)
=
t
A
A
{\displaystyle f(A)={}^{t}\!AA}
Montrer que
D
A
f
(
H
)
=
t
A
H
+
t
H
A
{\displaystyle \mathrm {D} _{A}f(H)={}^{t}\!AH+{}^{t}\!HA}
Soit
A
∈
O
n
(
R
)
{\displaystyle A\in \mathrm {O} _{n}(\mathbb {R} )}
S
∈
E
{\displaystyle S\in E}
H
=
1
2
A
S
{\displaystyle H={\frac {1}{2}}AS}
D
A
f
(
H
)
=
S
{\displaystyle \mathrm {D} _{A}f(H)=S}
O
n
(
R
)
{\displaystyle \mathrm {O} _{n}(\mathbb {R} )}
M
n
(
R
)
{\displaystyle \mathrm {M} _{n}(\mathbb {R} )}
n
(
n
−
1
)
/
2
{\displaystyle n(n-1)/2}
I
n
{\displaystyle \mathrm {I} _{n}}
{
X
∈
M
n
(
R
)
∣
t
X
=
−
X
}
{\displaystyle \{X\in \mathrm {M} _{n}(\mathbb {R} )\mid {}^{t}\!X=-X\}}
Solution
f
{\displaystyle f}
B
:
M
n
(
R
)
×
M
n
(
R
)
→
M
n
(
R
)
{\displaystyle B:\mathrm {M} _{n}(\mathbb {R} )\times \mathrm {M} _{n}(\mathbb {R} )\to \mathrm {M} _{n}(\mathbb {R} )}
(
t
⋅
,
i
d
)
{\displaystyle ({}^{t}\!\cdot ,\mathrm {id} )}
chap. 2 )
D
A
f
(
H
)
=
D
B
(
t
A
,
A
)
(
t
H
,
H
)
=
B
(
t
A
,
H
)
+
B
(
t
H
,
A
)
{\displaystyle \mathrm {D} _{A}f(H)=\mathrm {D} B_{({}^{t}\!A,A)}({}^{t}\!H,H)=B({}^{t}\!A,H)+B({}^{t}\!H,A)}
D
A
f
(
H
)
=
t
A
H
+
t
H
A
=
t
A
1
2
A
S
+
t
(
1
2
A
S
)
A
=
1
2
t
A
A
S
+
1
2
t
S
t
A
A
=
1
2
S
+
1
2
t
S
=
S
{\displaystyle \mathrm {D} _{A}f(H)={}^{t}\!AH+{}^{t}\!HA={}^{t}\!A{\frac {1}{2}}AS+{}^{t}\!({\frac {1}{2}}AS)A={\frac {1}{2}}{}^{t}\!AAS+{\frac {1}{2}}{}^{t}\!S{}^{t}\!AA={\frac {1}{2}}S+{\frac {1}{2}}{}^{t}\!S=S}
D
A
f
{\displaystyle \mathrm {D} _{A}f}
O
n
(
R
)
=
f
−
1
(
{
I
n
}
)
{\displaystyle \mathrm {O} _{n}(\mathbb {R} )=f^{-1}(\{\mathrm {I} _{n}\})}
M
n
(
R
)
{\displaystyle \mathrm {M} _{n}(\mathbb {R} )}
dim
M
n
(
R
)
−
dim
E
=
n
2
−
n
(
n
+
1
)
/
2
=
n
(
n
−
1
)
/
2
{\displaystyle \dim \mathrm {M} _{n}(\mathbb {R} )-\dim E=n^{2}-n(n+1)/2=n(n-1)/2}
I
n
{\displaystyle \mathrm {I} _{n}}
ker
(
D
I
n
f
)
=
{
H
∈
M
n
(
R
)
∣
t
H
+
H
=
0
}
{\displaystyle \ker(\mathrm {D} _{\mathrm {I} _{n}}f)=\{H\in \mathrm {M} _{n}(\mathbb {R} )\mid {}^{t}\!H+H=0\}}
Montrer que l'ensemble
S
:=
{
(
x
,
y
,
z
)
∈
R
3
∣
x
2
+
y
2
+
z
2
=
2
(
x
+
y
+
z
−
1
)
}
{\displaystyle S:=\{(x,y,z)\in \mathbb {R} ^{3}\mid x^{2}+y^{2}+z^{2}=2(x+y+z-1)\}}
Déterminer l'équation du plan tangent à
S
{\displaystyle S}
(
x
0
,
y
0
,
z
0
)
∈
S
{\displaystyle (x_{0},y_{0},z_{0})\in S}
Expliciter les deux cas particuliers
(
x
0
,
y
0
,
z
0
)
=
(
1
,
1
,
0
)
{\displaystyle (x_{0},y_{0},z_{0})=(1,1,0)}
(
x
0
,
y
0
,
z
0
)
=
(
1
,
1
,
2
)
{\displaystyle (x_{0},y_{0},z_{0})=(1,1,2)}
Solution
x
2
+
y
2
+
z
2
=
2
(
x
+
y
+
z
−
1
)
⟺
(
x
−
1
)
2
+
(
y
−
1
)
2
+
(
z
−
1
)
2
=
1
2
{\displaystyle x^{2}+y^{2}+z^{2}=2(x+y+z-1)\Longleftrightarrow (x-1)^{2}+(y-1)^{2}+(z-1)^{2}=1^{2}}
S
{\displaystyle S}
(
1
,
1
,
1
)
{\displaystyle (1,1,1)}
1
{\displaystyle 1}
En un point
M
0
=
(
x
0
,
y
0
,
z
0
)
{\displaystyle M_{0}=(x_{0},y_{0},z_{0})}
f
(
x
,
y
,
z
)
=
0
{\displaystyle f(x,y,z)=0}
grad
f
(
M
0
)
=
2
(
x
0
−
1
,
y
0
−
1
,
z
0
−
1
)
{\displaystyle \operatorname {grad} f(M_{0})=2(x_{0}-1,y_{0}-1,z_{0}-1)}
⟨
∇
f
→
(
M
0
)
,
M
0
M
→
⟩
=
0
{\displaystyle \langle {\overrightarrow {\nabla f}}(M_{0}),{\overrightarrow {M_{0}M}}\rangle =0}
2
{\displaystyle 2}
(
x
0
−
1
)
(
x
−
x
0
)
+
(
y
0
−
1
)
(
y
−
y
0
)
+
(
z
0
−
1
)
(
z
−
z
0
)
=
0
{\displaystyle (x_{0}-1)(x-x_{0})+(y_{0}-1)(y-y_{0})+(z_{0}-1)(z-z_{0})=0}
(
x
0
,
y
0
,
z
0
)
∈
S
{\displaystyle (x_{0},y_{0},z_{0})\in S}
x
0
x
+
y
0
y
+
z
0
z
=
2
(
x
0
+
y
0
+
z
0
−
1
)
{\displaystyle x_{0}x+y_{0}y+z_{0}z=2(x_{0}+y_{0}+z_{0}-1)}
On vérifie que
f
{\displaystyle f}
M
0
=
(
1
,
1
,
0
)
{\displaystyle M_{0}=(1,1,0)}
M
1
=
(
1
,
1
,
2
)
{\displaystyle M_{1}=(1,1,2)}
S
{\displaystyle S}
S
{\displaystyle S}
en
M
0
{\displaystyle M_{0}}
(
1
−
1
)
(
x
−
1
)
+
(
1
−
1
)
(
y
−
1
)
+
(
0
−
1
)
(
z
−
0
)
=
0
{\displaystyle (1-1)(x-1)+(1-1)(y-1)+(0-1)(z-0)=0}
z
=
0
{\displaystyle z=0}
en
M
1
{\displaystyle M_{1}}
(
1
−
1
)
(
x
−
1
)
+
(
1
−
1
)
(
y
−
1
)
+
(
2
−
1
)
(
z
−
2
)
=
0
{\displaystyle (1-1)(x-1)+(1-1)(y-1)+(2-1)(z-2)=0}
z
=
2
{\displaystyle z=2}
On peut remarquer que ces deux plans sont parallèles, ce qui n'a rien de surprenant puisque ces deux points de la sphère sont diamétralement opposés.
Trouver l'équation cartésienne et paramétrique du plan tangent pour chaque surface ci-dessous, au point
(
x
0
,
y
0
,
z
0
)
{\displaystyle (x_{0},y_{0},z_{0})}
z
=
19
−
x
2
−
y
2
,
(
x
0
,
y
0
,
z
0
)
=
(
1
,
3
,
3
)
{\displaystyle z={\sqrt {19-x^{2}-y^{2}}},\quad (x_{0},y_{0},z_{0})=(1,3,3)}
z
=
sin
(
π
x
y
)
exp
(
2
x
2
y
−
1
)
,
(
x
0
,
y
0
,
z
0
)
=
(
1
,
1
/
2
,
1
)
{\displaystyle z=\sin(\pi xy)\exp(2x^{2}y-1),\quad (x_{0},y_{0},z_{0})=(1,1/2,1)}
z
=
8
−
x
2
−
y
2
,
(
x
0
,
y
0
,
z
0
)
=
(
1
,
2
,
3
)
{\displaystyle z=8-x^{2}-y^{2},\quad (x_{0},y_{0},z_{0})=(1,2,3)}
Solution
http://exo7.emath.fr/ficpdf/fic00063.pdf exercice 1 [002628] pour les questions 1 et 2.
Le plan tangent, en un point
(
x
0
,
y
0
,
z
0
)
{\displaystyle (x_{0},y_{0},z_{0})}
x
2
+
y
2
+
z
2
=
19
{\displaystyle x^{2}+y^{2}+z^{2}=19}
2
(
x
0
,
y
0
,
z
0
)
{\displaystyle 2(x_{0},y_{0},z_{0})}
cartésienne :
x
0
x
+
y
0
y
+
z
0
z
=
19
{\displaystyle x_{0}x+y_{0}y+z_{0}z=19}
(
x
0
,
y
0
,
z
0
)
=
(
1
,
3
,
3
)
{\displaystyle (x_{0},y_{0},z_{0})=(1,3,3)}
x
+
3
y
+
3
z
=
19
{\displaystyle x+3y+3z=19}
paramétrique : par exemple,
x
=
x
0
+
s
z
0
,
y
=
y
0
+
t
z
0
,
z
=
z
0
−
s
x
0
−
t
y
0
{\displaystyle x=x_{0}+sz_{0},\;y=y_{0}+tz_{0},\;z=z_{0}-sx_{0}-ty_{0}}
(
x
0
,
y
0
,
z
0
)
=
(
1
,
3
,
3
)
{\displaystyle (x_{0},y_{0},z_{0})=(1,3,3)}
x
=
1
+
3
s
,
y
=
3
+
3
t
,
z
=
3
−
s
−
3
t
{\displaystyle x=1+3s,\;y=3+3t,\;z=3-s-3t}
Le plan tangent, en un point
(
x
0
,
y
0
,
z
0
)
{\displaystyle (x_{0},y_{0},z_{0})}
z
=
sin
(
π
x
y
)
exp
(
2
x
2
y
−
1
)
{\displaystyle z=\sin(\pi xy)\exp(2x^{2}y-1)}
(
1
,
0
,
(
y
0
π
cos
(
π
x
0
y
0
)
+
4
x
0
y
0
)
exp
(
2
x
0
2
y
0
−
1
)
)
{\displaystyle \left(1,0,(y_{0}\pi \cos(\pi x_{0}y_{0})+4x_{0}y_{0})\exp(2x_{0}^{2}y_{0}-1)\right)}
(
0
,
1
,
(
x
0
π
cos
(
π
x
0
y
0
)
+
2
x
0
2
)
exp
(
2
x
0
2
y
0
−
1
)
)
{\displaystyle \left(0,1,(x_{0}\pi \cos(\pi x_{0}y_{0})+2x_{0}^{2})\exp(2x_{0}^{2}y_{0}-1)\right)}
cartésienne :
z
=
z
0
+
exp
(
2
x
0
2
y
0
−
1
)
[
(
x
−
x
0
)
(
y
0
π
cos
(
π
x
0
y
0
)
+
4
x
0
y
0
)
+
(
y
−
y
0
)
(
x
0
π
cos
(
π
x
0
y
0
)
+
2
x
0
2
)
]
{\displaystyle z=z_{0}+\exp(2x_{0}^{2}y_{0}-1)[(x-x_{0})(y_{0}\pi \cos(\pi x_{0}y_{0})+4x_{0}y_{0})+(y-y_{0})(x_{0}\pi \cos(\pi x_{0}y_{0})+2x_{0}^{2})]}
(
x
0
,
y
0
,
z
0
)
=
(
1
,
1
/
2
,
1
)
{\displaystyle (x_{0},y_{0},z_{0})=(1,1/2,1)}
z
=
2
(
x
+
y
−
1
)
{\displaystyle z=2(x+y-1)}
paramétrique : par exemple,
x
=
x
0
+
s
,
y
=
y
0
+
t
,
z
=
z
0
+
s
(
y
0
π
cos
(
π
x
0
y
0
)
+
4
x
0
y
0
)
exp
(
2
x
0
2
y
0
−
1
)
+
t
(
x
0
π
cos
(
π
x
0
y
0
)
+
2
x
0
2
)
exp
(
2
x
0
2
y
0
−
1
)
{\displaystyle x=x_{0}+s,\;y=y_{0}+t,\;z=z_{0}+s(y_{0}\pi \cos(\pi x_{0}y_{0})+4x_{0}y_{0})\exp(2x_{0}^{2}y_{0}-1)+t(x_{0}\pi \cos(\pi x_{0}y_{0})+2x_{0}^{2})\exp(2x_{0}^{2}y_{0}-1)}
(
x
0
,
y
0
,
z
0
)
=
(
1
,
1
/
2
,
1
)
{\displaystyle (x_{0},y_{0},z_{0})=(1,1/2,1)}
x
=
1
+
s
,
y
=
1
/
2
+
t
,
z
=
1
+
2
s
+
2
t
{\displaystyle x=1+s,\;y=1/2+t,\;z=1+2s+2t}
Le plan tangent, en un point
(
x
0
,
y
0
,
z
0
)
{\displaystyle (x_{0},y_{0},z_{0})}
z
=
8
−
x
2
−
y
2
{\displaystyle z=8-x^{2}-y^{2}}
(
1
,
0
,
−
2
x
0
)
{\displaystyle \left(1,0,-2x_{0}\right)}
(
0
,
1
,
−
2
y
0
)
{\displaystyle \left(0,1,-2y_{0}\right)}
cartésienne :
2
x
0
x
+
2
y
0
y
+
z
=
x
0
2
+
y
0
2
+
8
{\displaystyle 2x_{0}x+2y_{0}y+z=x_{0}^{2}+y_{0}^{2}+8}
(
x
0
,
y
0
,
z
0
)
=
(
1
,
2
,
3
)
{\displaystyle (x_{0},y_{0},z_{0})=(1,2,3)}
2
x
+
4
y
+
z
=
13
{\displaystyle 2x+4y+z=13}
paramétrique : par exemple,
x
=
x
0
+
s
,
y
=
y
0
+
t
,
z
=
z
0
−
2
x
0
s
−
2
y
0
t
{\displaystyle x=x_{0}+s,\;y=y_{0}+t,\;z=z_{0}-2x_{0}s-2y_{0}t}
(
x
0
,
y
0
,
z
0
)
=
(
1
,
2
,
3
)
{\displaystyle (x_{0},y_{0},z_{0})=(1,2,3)}
x
=
1
+
s
,
y
=
2
+
t
,
z
=
3
−
2
s
−
4
t
{\displaystyle x=1+s,\;y=2+t,\;z=3-2s-4t}
Sur le paraboloïde elliptique
z
=
4
x
2
+
y
2
{\displaystyle z=4x^{2}+y^{2}}
x
+
2
y
+
z
=
6
{\displaystyle x+2y+z=6}
Même question avec le plan
3
x
+
5
y
−
2
z
=
3
{\displaystyle 3x+5y-2z=3}
Solution
http://exo7.emath.fr/ficpdf/fic00063.pdf exercice 3 [002630]
Le plan tangent au paraboloïde en un point
(
x
,
y
,
z
)
{\displaystyle (x,y,z)}
z
=
4
x
2
+
y
2
{\displaystyle z=4x^{2}+y^{2}}
(
8
x
,
2
y
,
−
1
)
{\displaystyle (8x,2y,-1)}
au vecteur
(
1
,
2
,
1
)
{\displaystyle (1,2,1)}
x
=
1
8
{\displaystyle x={\frac {1}{8}}}
y
=
−
1
{\displaystyle y=-1}
z
=
17
16
{\displaystyle z={\frac {17}{16}}}
au vecteur
(
3
,
5
,
−
2
)
{\displaystyle (3,5,-2)}
x
=
3
16
{\displaystyle x={\frac {3}{16}}}
y
=
5
4
{\displaystyle y={\frac {5}{4}}}
z
=
109
64
{\displaystyle z={\frac {109}{64}}}
Soit
S
{\displaystyle S}
x
=
(
1
+
v
2
)
cos
u
,
y
=
(
1
+
v
2
)
sin
u
,
z
=
v
{\displaystyle x=\left(1+v^{2}\right)\cos u,\;y=\left(1+v^{2}\right)\sin u,\;z=v}
(
u
,
v
)
∈
[
0
,
2
π
[
×
]
−
1
,
1
[
{\displaystyle (u,v)\in \left[0,2\pi \right[\times \left]-1,1\right[}
Trouver l'ensemble des points de
S
{\displaystyle S}
On pose
f
(
x
,
y
)
=
x
3
+
y
3
−
x
2
−
y
2
{\displaystyle f(x,y)=x^{3}+y^{3}-x^{2}-y^{2}}
Calculer le gradient
grad
(
f
)
{\displaystyle \operatorname {grad} (f)}
D
f
{\displaystyle \mathrm {D} f}
f
{\displaystyle f}
Calculer l'équation de la tangente à la courbe d'équation
f
(
x
,
y
)
=
0
{\displaystyle f(x,y)=0}
(
1
,
1
)
{\displaystyle (1,1)}
(
0
,
1
)
{\displaystyle (0,1)}
(
1
,
0
)
{\displaystyle (1,0)}
Solution
grad
(
f
)
(
x
,
y
)
=
(
3
x
2
−
2
x
,
3
y
2
−
2
y
)
{\displaystyle \operatorname {grad} (f)(x,y)=(3x^{2}-2x,3y^{2}-2y)}
D
f
(
x
,
y
)
(
h
,
k
)
=
(
3
x
2
−
2
x
)
h
+
(
3
y
2
−
2
y
)
k
{\displaystyle \mathrm {D} f_{(x,y)}(h,k)=(3x^{2}-2x)h+(3y^{2}-2y)k}
La tangente en un point
(
a
,
b
)
{\displaystyle (a,b)}
grad
(
f
)
(
a
,
b
)
{\displaystyle \operatorname {grad} (f)(a,b)}
(
x
−
a
)
(
3
a
2
−
2
a
)
+
(
y
−
b
)
(
3
b
2
−
2
b
)
=
0
{\displaystyle (x-a)(3a^{2}-2a)+(y-b)(3b^{2}-2b)=0}
si
(
a
,
b
)
=
(
1
,
1
)
{\displaystyle (a,b)=(1,1)}
x
+
y
=
2
{\displaystyle x+y=2}
si
(
a
,
b
)
=
(
0
,
1
)
{\displaystyle (a,b)=(0,1)}
y
=
1
{\displaystyle y=1}
si
(
a
,
b
)
=
(
1
,
0
)
{\displaystyle (a,b)=(1,0)}
x
=
1
{\displaystyle x=1}
Soit
S
{\displaystyle S}
z
=
x
+
y
2
{\displaystyle z=x+y^{2}}
Déterminer le plan tangent à
S
{\displaystyle S}
Mêmes questions au point
(
1
,
1
,
2
)
{\displaystyle (1,1,2)}
Solution
Ce plan
P
{\displaystyle P}
z
=
x
{\displaystyle z=x}
M
(
x
,
y
)
=
(
x
,
y
,
x
+
y
2
)
∈
S
{\displaystyle M(x,y)=(x,y,x+y^{2})\in S}
(
x
,
y
,
x
)
∈
P
{\displaystyle (x,y,x)\in P}
M
(
x
,
y
)
{\displaystyle M(x,y)}
Ce plan
Q
{\displaystyle Q}
z
−
2
=
x
−
1
+
2
(
y
−
1
)
{\displaystyle z-2=x-1+2(y-1)}
z
=
x
+
2
y
−
1
{\displaystyle z=x+2y-1}
M
(
x
,
y
)
=
(
x
,
y
,
x
+
y
2
)
∈
S
{\displaystyle M(x,y)=(x,y,x+y^{2})\in S}
(
x
,
y
,
x
+
2
y
−
1
)
∈
Q
{\displaystyle (x,y,x+2y-1)\in Q}
M
(
x
,
y
)
{\displaystyle M(x,y)}
y
2
−
2
y
+
1
=
(
y
−
1
)
≥
0
{\displaystyle y^{2}-2y+1=(y-1)\geq 0}




































![{\displaystyle z={\sqrt[{3}]{xy}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7668f89e2b339ec97159224b55afc47753cf227d)



![{\displaystyle z_{0}={\sqrt[{3}]{x_{0}y_{0}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/786a431b1a162e2a60f01dce33dbe7e1129a4b80)
![{\displaystyle {\begin{aligned}{\sqrt[{3}]{\left(x_{0}+u\right)\left(y_{0}+v\right)}}&=z_{0}\left(1+{\frac {u}{x_{0}}}\right)^{1/3}\left(1+{\frac {v}{y_{0}}}\right)^{1/3}\\&=z_{0}\left(1+{\frac {u}{3x_{0}}}-{\frac {u^{2}}{9x_{0}^{2}}}\right)\left(1+{\frac {v}{3y_{0}}}-{\frac {v^{2}}{9y_{0}^{2}}}\right)+o\left(u^{2}+v^{2}\right)\\&=z_{0}+{\frac {z_{0}}{3x_{0}}}u+{\frac {z_{0}}{3y_{0}}}v+{\frac {z_{0}}{9}}\left(-{\frac {u^{2}}{x_{0}^{2}}}+{\frac {uv}{x_{0}y_{0}}}-{\frac {v^{2}}{y_{0}^{2}}}\right)+o\left(u^{2}+v^{2}\right).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa1472e1dad822c186b8fc37d5d20d621bc1b142)










































![{\displaystyle C_{2}=\{({\sqrt[{3}]{y^{2}}},y)\mid y\in \mathbb {R} \}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3b4d6e3d3ca8d4dc4bccf5ab13f9c4ea8fd2de9)











































































































![{\displaystyle z=z_{0}+\exp(2x_{0}^{2}y_{0}-1)[(x-x_{0})(y_{0}\pi \cos(\pi x_{0}y_{0})+4x_{0}y_{0})+(y-y_{0})(x_{0}\pi \cos(\pi x_{0}y_{0})+2x_{0}^{2})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f545eacf31dc5926cf6b0dd6cc895ccbdcc917bb)

























![{\displaystyle (u,v)\in \left[0,2\pi \right[\times \left]-1,1\right[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d297f78b26d0d6d4d13aa1e89f663ece5a2f7162)
































