Sommation/Formule du binôme
Lemme préliminaire
[modifier | modifier le wikicode]Nous aurons besoin pour la démonstration de la formule du binôme du lemme suivant sur les coefficients binomiaux :
|
Démonstration de la formule de Pascal On a :
Voir aussi la démonstration combinatoire (chap. 1) de la formule de Vandermonde , dont la formule de Pascal est le cas particulier . |
Démonstration de la formule du binôme
[modifier | modifier le wikicode]Tout le monde connaît bien la formule :
Et probablement aussi la formule :
Ces deux formules sont des cas particuliers d'une formule plus générale appelée formule du binôme que l’on énonce ainsi :
Soient, dans un anneau, deux éléments et tels que (par exemple : deux nombres complexes).
Pour tout entier naturel , nous avons :
Au premier rang, on a bien :
- .
Pour n entier supérieur ou égal à 1, nous démontrerons la formule du binôme par récurrence. (On a traité à part le cas n = 0 car au cours de la démonstration ci-dessous apparaîtront des sommes de la forme , qui n'auraient pas de sens dans ce cas. Un autre démonstration par récurrence, consistant à intégrer au lieu de multiplier — cf. exercice 4-9 — évite cet écueil.)
Initialisation
Au premier rang, on a bien :
- .
Caractère héréditaire
Soit n un entier supérieur ou égal à 1 tel que l'hypothèse de récurrence soit vraie, montrons que la relation est vraie aussi pour n + 1 :
Par hypothèse de récurrence :
Par distributivité de la multiplication par rapport à l'addition :
Par factorisation :
En utilisant la formule de Pascal :
le principe de récurrence termine alors la démonstration.
|
Remarque Comme l’objet de notre propos est de réaliser des sommations, il est nécessaire de bien connaître la formule du binôme dans les deux sens. Il est donc recommandé de bien la connaître aussi sous la forme :
|
Triangle de Pascal
[modifier | modifier le wikicode]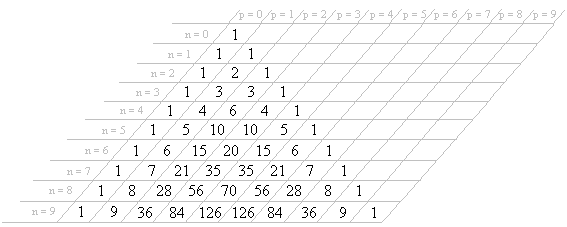
On peut commodément représenter sous forme de tableau triangulaire la valeur des . Sur le tableau ci-contre, à l'intersection de la ligne n et de la colonne p, nous avons la valeur numérique de . Ce tableau, appelé triangle de Pascal, donne les coefficients du développement d'une expression de la forme (a + b)n. Supposons que l’on veuille, par exemple, calculer (a + b)5. En utilisant la ligne correspondant à n = 5, nous voyons que nous obtenons :

Généralement, les lignes et les colonnes ne sont pas représentées et nous avons simplement le tableau ci-contre à gauche. C'est à nous d'imaginer mentalement quelle est la valeur de n et de p. Il suffit de remarquer que la valeur de n est la première valeur différente de 1 que l’on trouve sur la ligne et cette première valeur différente de 1 correspond à la colonne p = 1.

Pour construire ce triangle, nous utilisons la formule de Pascal qui se traduit par le fait que chaque nombre du triangle est la somme des deux nombres qui sont immédiatement dessus. Voir l'animation à droite.
Pour plus de détails, voir l'article « Triangle de Pascal » sur Wikipédia.
























