Signaux physiques (PCSI)/Optique géométrique : lentilles minces
Retour sur les systèmes dioptriques « centrés », exemple des lentilles sphériques, cas particulier des précédentes : les lentilles minces
[modifier | modifier le wikicode]Rappel : Un système dioptrique centré est un cas particulier de « système optique (dioptrique) » paragraphe du chap. de la leçon « Signaux physiques (PCSI) » à caractère « centré » paragraphe du chap. de la leçon « Signaux physiques (PCSI) » c.-à-d. possédant un axe de symétrie de révolution.
Retour sur les systèmes dioptriques « centrés »
[modifier | modifier le wikicode]Il n'y a « pas stigmatisme rigoureux » pour les systèmes dioptriques centrés [1], mais on admet que l'utilisation de « rayons incidents paraxiaux » voir le paragraphe « énoncé des conditions de Gauss de stigmatisme approché d'un système optique centré » [2] du chap. de la leçon « Signaux physiques (PCSI) » confère aux systèmes dioptriques centrés le « stigmatisme approché » ;
de même il n'y a « pas aplanétisme rigoureux » pour les systèmes dioptriques centrés, mais on admet que l'utilisation d'« objets linéiques transverses “vus de la face d'entrée” sous un petit angle » voir le paragraphe « conditions supplémentaires de Gauss d'aplanétisme approché d'un système optique centré » [2] du chap. de la leçon « Signaux physiques (PCSI) » [3] confère aux systèmes dioptriques centrés l'« aplanétisme approché » ;
un système dioptrique centré est dit

- « afocal » si le point à l'infini de l'axe optique principal est un point double, cela entraîne que
« afocal » tout rayon incident à l'axe optique principal émerge parallèlement à ce même axe, et que
« afocal » tout pinceau incident à l'axe optique principal émerge en un pinceau à ce même axe mais non nécessairement de même diamètre voir figure ci-contre ;
- « afocal » comme il y a aplanétisme approché, « un objet linéique transverse du plan de front à l'infini donne une image linéique transverse du même plan de front à l'infini » mais non nécessairement superposable, cela entraîne que
« afocal » tout pinceau incident de direction inclinée relativement à l'axe optique principal émerge en un pinceau d'inclinaison par rapport à ce même axe a priori différente voir figure ci-contre ;

- « focal » si le point objet à l'infini de l'axe optique principal est conjugué d'un point image à distance finie, ce dernier étant le « foyer principal image » noté soit «» voir la disposition de gauche de la figure ci-contre et
« focal » si le point image à l'infini de l'axe optique principal a pour conjugué un point objet à distance finie, ce dernier étant le « foyer principal objet » noté soit «» voir la disposition de droite de la figure ci-contre ;

- « focal » chacun des points du « plan focal image », c.-à-d. du plan de front passant par le foyer principal image , étant l'image du point objet à l'infini d'une direction inclinée relativement à l'axe optique principal est appelé « foyer secondaire image [4] associé à la direction soit » voir la disposition de gauche de la figure ci-contre et
« focal » chacun des points du « plan focal objet », c.-à-d. du plan de front passant par le foyer principal objet , étant conjugué du point image à l'infini d'une direction inclinée relativement à l'axe optique principal est appelé « foyer secondaire objet [5] associé à la direction soit » voir la disposition de droite de la figure ci-contre.
Exemple de systèmes dioptriques « centrés » : les lentilles sphériques
[modifier | modifier le wikicode]Une lentille sphérique « épaisse » [6] est la juxtaposition de deux « dioptres sphériques » [7] de même espace optique intermédiaire d'indice , les deux espaces optiques extrêmes celui d'entrée et celui de sortie étant le plus souvent l'air d'indice ;
le 1er dioptre sphérique « le dioptre d'entrée » noté [8] ayant pour centre de courbure et pour sommet [9] et
le 2ème dioptre sphérique « le dioptre de sortie » noté [10] ayant pour centre de courbure et pour sommet [9],
on algébrise physiquement l'axe optique principal de la face d'entrée vers la face de sortie en définissant l'épaisseur de la lentille sphérique par [11] ;
on introduit également les rayons de courbure « algébrisés » [12] :
- le rayon de courbure algébrisé de la face d'entrée [13],
- le rayon de courbure algébrisé de la face de sortie [14].
-
Exemples de lentilles convergentes : biconvexe, plan-convexe et ménisque convergent
-
Exemples de lentilles divergentes : biconcave, plan-concave et ménisque divergent
Une lentille sphérique peut être :
- biconvexe voir ci-dessus le 1er schéma à partir de la gauche si la face d'entrée est « convexe », la face de sortie étant « concave » [15] on peut citer un cas particulier de lentille biconvexe, la lentille « boule », les rayons de courbure non algébrisés y sont les mêmes, les centres de courbure étant confondus et l'épaisseur égale à deux fois le rayon de courbure commun non algébrisé [16],
- plan - convexe voir ci-dessus les 2èmes schémas à partir de la gauche si la face d'entrée est « convexe », la face de sortie étant « plane » [17] cas particulier de lentille plan - convexe, la lentille « demi-boule », le centre de courbure de la face sphérique étant confondu avec le sommet de la face plane et l'épaisseur étant égale au rayon de courbure non algébrisé de la face sphérique [18],
- ménisque convergent voir ci-dessus les 3èmes schémas à partir de la gauche si la face d'entrée est « convexe », la face de sortie étant « convexe » de rayon non algébrisé plus grand que celui de la face d'entrée [19],
- biconcave voir ci-dessus le 4ème schéma à partir de la gauche si la face d'entrée est « concave », la face de sortie étant « convexe » [15],
- plan - concave voir ci-dessus les 5èmes schémas à partir de la gauche si la face d'entrée est « concave », la face de sortie étant « plane » [20] et
- ménisque divergent voir ci-dessus les 6èmes schémas à partir de la gauche si la face d'entrée est « concave », la face de sortie étant « concave » de rayon non algébrisé plus grand que celui de la face d'entrée [21].

Caractère « stigmatique non rigoureux mais approché » d'une lentille « demi-boule » pour le point à l'infini de son axe optique principal voir schéma ci-contre, la demi-boule étant d'indice «» :
les rayons incidents étant à l'axe optique principal traversent le 1er dioptre plan air - verre sans être déviés puis
les rayons incidents étant // à l'axe optique principal arrivant sur le 2ème dioptre sphérique verre - air sous un angle d'incidence d'autant plus grand en valeur absolue que le point d'incidence sur ce dioptre sphérique est éloigné de l'axe optique principal ,
les rayons incidents étant // à l'axe optique principal subissent une réflexion totale sur ce dioptre sphérique verre - air dès lors que « leur angle d'incidence est, en valeur absolue à l'angle limite du dioptre [22] » [23] c.-à-d. pour les rayons incidents dont la distance à l'axe optique principal est ou
les rayons incidents étant // à l'axe optique principal émergent par réfraction sur ce dioptre sphérique verre - air en suivant les 1ère et 2ème lois de Snell-Descartes [24], [25] de la réfraction [26] dès lors que « leur angle d'incidence est, en valeur absolue à l'angle limite du dioptre [22] les rayons réfractés étant d'autant plus inclinés en direction de l'axe optique principal que la distance séparant le rayon incident de est grande [27] ;
- on observe l'absence de convergence ponctuelle d'un faisceau parallèle à l'axe optique principal couvrant la quasi totalité de la face d'entrée voir schéma ci-dessus à droite d'où l'« absence de stigmatisme rigoureux de la lentille demi-boule pour le point à l'infini de l'axe optique principal » [27], par contre
- si on limite suffisamment la largeur du faisceau parallèle à l'aide d'un diaphragme positionné contre la face d'entrée en rouge sur le schéma ci-dessus à droite, on observe l'apparition d'une « convergence ponctuelle en » [28], ce qui justifie le « stigmatisme approché de la lentille demi-boule pour le point à l'infini de l'axe optique principal ».
Cas particulier de lentilles sphériques : les lentilles minces
[modifier | modifier le wikicode]Une lentille sphérique est dite « mince » si « son épaisseur est très petite » [29] soit encore si « les sommets des faces d'entrée et de sortie peuvent être confondus » ou «» ;
nous admettrons le stigmatisme et l'aplanétisme « approchés » [30] d'une lentille sphérique mince dans les conditions de Gauss [2] à savoir
- l'utilisation de « rayons incidents paraxiaux » voir le paragraphe « énoncé des conditions de Gauss de stigmatisme approché d'un système optique centré » [2] du chap. de la leçon « Signaux physiques (PCSI) » pour le stigmatisme approché et
- celle d'« objets linéiques transverses “vus de la face d'entrée” sous un petit angle » voir le paragraphe « conditions supplémentaires de Gauss d'aplanétisme approché d'un système optique centré » [2] du chap. de la leçon « Signaux physiques (PCSI) » [3] pour l'aplanétisme approché.
Centre optique d'une lentille mince, son axe optique principal et ses axes optiques secondaires
[modifier | modifier le wikicode]Définition du centre optique d'une lentille mince
[modifier | modifier le wikicode]Le « centre optique d'une lentille mince, usuellement noté », est le « sommet commun des dioptres d'entrée et de sortie de la lentille sphérique que la lentille mince modélise dans les conditions de faible épaisseur ».
Axe optique principal d'une lentille mince
[modifier | modifier le wikicode] L'« axe optique principal d'une lentille mince » est l'« axe de symétrie, noté , de la lentille sphérique que la lentille mince modélise dans les conditions de faible épaisseur »,
L'« axe optique principal d'une lentille mince » son algébrisation physique est dans le sens de la propagation comme pour tout système dioptrique centré ;
L'« axe optique principal d'une lentille mince » « est la commune en , centre optique de la lentille mince, aux faces d'entrée et de sortie de cette dernière ».
Axes optiques secondaires d'une lentille mince
[modifier | modifier le wikicode] Les « axes optiques secondaires d'une lentille mince » sont les « associations d'un rayon incident passant par le centre optique , incliné par rapport à l'axe optique principal , et
Les « axes optiques secondaires d'une lentille mince » sont les « associations de l'émergent correspondant » [31].
Rappel des conditions de Gauss de stigmatisme et d'aplanétisme approchés d'une lentille mince
[modifier | modifier le wikicode]Conditions de Gauss du stigmatisme approché d'une lentille mince : « les rayons incidents doivent être paraxiaux » c.-à-d. peu inclinés relativement à l'axe optique principal et dont le point d'incidence reste proche du centre optique [32].
Conditions supplémentaires de Gauss d'aplanétisme approché d'une lentille mince : « si l'objet linéique transverse n'est pas proche du centre optique il doit être vu de sous un petit angle » et
Conditions supplémentaires de Gauss d'aplanétisme approché d'une lentille mince : « s'il en est proche il doit être de petites dimensions » [33].
Propriété d'un rayon incident passant par le centre optique d'une lentille mince, stigmatisme rigoureux de cette dernière pour son centre optique et notion de point double
[modifier | modifier le wikicode]Propriété d'un rayon incident passant par le centre optique d'une lentille mince
[modifier | modifier le wikicode]« Tout rayon incident passant par le centre optique d'une lentille mince » n'est pas dévié « quelle que soit l'inclinaison du rayon par rapport à l'axe optique principal ».

Tentative de justification à partir de l'observation du tracé sur une lentille sphérique épaisse biconvexe quand cette dernière devient mince :
Tentative de justification Ci-contre un rayon incident de point d'incidence sur la face d'entrée d'une lentille sphérique d'épaisseur donnant
Tentative de justification Ci-contre un rayon émergent de point d'incidence sur la face de sortie de cette dernière avec
Tentative de justification Ci-contre un rayon intermédiaire coupant l'axe optique principal de celle-ci en un point ;
Tentative de justification en le rayon intermédiaire s'est rapproché de la normale au dioptre d'entrée par rapport au rayon incident [34] et
Tentative de justification en il est plus éloigné de la normale au dioptre de sortie que le rayon émergent [35],
Tentative de justification ces deux effets antagonistes n'étant pas réalisés relativement à une même direction la normale au dioptre d'entrée en n'étant pas confondue avec la normale au dioptre de sortie en , cela fournit une direction pour le rayon émergent a priori différente de celle du rayon incident ;
Tentative de justification toutefois si on fait tendre, par la pensée, l'épaisseur vers , le point et le point tendent tous deux vers le centre optique de la lentille mince qui modélise la lentille sphérique d'épaisseur infiniment petite et
Tentative de justification toutefois si on fait tendre, par la pensée, l'épaisseur e vers 0, la normale au dioptre d'entrée en et celle au dioptre de sortie en tendent toutes deux vers la normale commune aux faces d'entrée et de sortie de la lentille mince en c.-à-d. vers l'axe optique principal de cette dernière,
Tentative de justification toutefois si on fait tendre, par la pensée, l'épaisseur e vers 0, le rayon incident tendant vers un rayon incident faisant l'angle d'incidence avec ,
Tentative de justification toutefois si on fait tendre, par la pensée, l'épaisseur e vers 0, le rayon intermédiaire tendant vers un rayon intermédiaire de longueur tendant vers faisant un angle avec et
Tentative de justification toutefois si on fait tendre, par la pensée, l'épaisseur e vers 0, le rayon émergent tendant vers un rayon émergent faisant l'angle d'émergence avec
Tentative de justification toutefois si on fait tendre, par la pensée, l'épaisseur e vers 0, tels que «» c.-à-d. tels que «», donc une absence de déviation du rayon émergent relativement au rayon incident et ceci quelle que soit la valeur de l'angle d'incidence.
Conséquence sur les axes optiques secondaires d'une lentille mince
[modifier | modifier le wikicode]Une 1ère conséquence est qu'« un axe optique secondaire d'une lentille mince formé d'un rayon incident passant par le centre optique de cette dernière en étant incliné d'un angle relativement à l'axe optique principal et de l'émergent correspondant » est une « droitepassant par en étant inclinée de l'angle relativement à », l'inclinaison pouvant être quelconque.
Centre optique, point double de la lentille mince et stigmatisme rigoureux de cette dernière pour le centre optique
[modifier | modifier le wikicode]Une 2ème conséquence est qu'« un faisceau convergent au centre optique d'une lentille mince poursuit sans déviation en divergeant à partir de » et on en déduit que :
- étant sa propre image est un « point double »,
- le caractère ponctuel de l'image étant indépendant de l'ouverture du faisceau, « la lentille sphérique mince est stigmatique rigoureux pour le centre optique ».
Caractère focal d'une lentille mince, foyers principal objet et principal image, plans focaux, foyers secondaire objet et secondaire image associés à un axe optique secondaire
[modifier | modifier le wikicode]Lentille sphérique mince : système focal
[modifier | modifier le wikicode]Une lentille sphérique mince est un système « focal » c.-à-d. que
- le point à l'infini de l'axe optique principal a pour image un point de à distance finie [36] et
- il existe un point de à distance finie ayant pour image le point à l'infini de [37] ;
on peut également dire que « le point à l'infini den'est pas un point double ».
Foyer principal objet, foyer principal image
[modifier | modifier le wikicode]Le « foyer principal objet d'une lentille mince » est le « point de l'axe optique principal ayant pour image le point à l'infini de »
Le « foyer principal objet Fo d'une lentille mince »« tout rayon incident passant réellement ou virtuellement par émerge parallèlement à l'axe optique principal ».
Le « foyer principal image d'une lentille mince » est le « point de l'axe optique principal , image de le point à l'infini de »
Le « foyer principal image Fi d'une lentille mince »« tout rayon incident à l'axe optique principal émerge en passant réellement ou virtuellement par ».
On établit que « et occupent des positions géométriquement symétriques relativement à » [38].
On distingue deux types de lentilles minces suivant le caractère réel ou virtuel des foyers principaux :
- les lentilles convergentes biconvexe, plan convexe et ménisque convergent[39] pour lesquelles les foyers principaux objet et image sont réels voir ci-dessous à gauche avec la représentation symbolique d'une lentille convergente et
- les lentilles divergentes biconcave, plan concave et ménisque divergent[40] pour lesquelles les foyers principaux objet et image sont virtuels voir ci-dessous à droite avec la représentation symbolique d'une lentille divergente.
-
Positionnement des foyers principaux objet et image d'une lentille mince convergente avec la représentation symbolique de cette dernière
-
Positionnement des foyers principaux objet et image d'une lentille mince divergente avec la représentation symbolique de cette dernière
Plan focal objet, plan focal image, foyer secondaire objet associé à un axe optique secondaire, foyer secondaire image associé à un axe optique secondaire
[modifier | modifier le wikicode]Le « plan focal objet est le plan de front passant par le foyer principal objet », il est de même nature que le foyer principal objet à savoir « réel pour une lentille convergente » et « virtuel pour une lentille divergente » ;
le « plan focal image est le plan de front passant par le foyer principal image », il est de même nature que le foyer principal image à savoir « réel pour une lentille convergente » et « virtuel pour une lentille divergente ».
L'« intersection d'un axe optique secondaire avec le plan focal objet » définit « le foyer secondaire objet associé à cet axe optique secondaire » noté «» [41] ;
L'« intersection d'un axe optique secondaire δ avec le plan focal objet » c'est aussi, dans la mesure où l'axe optique secondaire est peu incliné relativement à l'axe optique principal [42], « le point de l'axe optique secondaire ayant pour image le point à l'infini de cet axe »
L'« intersection d'un axe optique secondaire δ avec le plan focal objet » « tout rayon incident passant réellement ou virtuellement par émerge parallèlement à » [43] ;
l'« intersection d'un axe optique secondaire avec le plan focal image » définit « le foyer secondaire image associé à cet axe optique secondaire » noté «» [44] ;
l'« intersection d'un axe optique secondaire δ avec le plan focal image » c'est aussi, dans la mesure où l'axe optique secondaire est peu incliné relativement à l'axe optique principal [42], « le point de l'axe optique secondaire, image du point à l'infini de cet axe »
l'« intersection d'un axe optique secondaire δ avec le plan focal image » « tout rayon incident à émerge en passant réellement ou virtuellement par » [43].
Distance focale et vergence d'une lentille mince
[modifier | modifier le wikicode]La « distance focale objet d'une lentille mince est la distance algébrique » [45], [46], elle est telle que :
- « pour une lentille mince convergente » et
- « pour une lentille mince divergente » ;
la « distance focale image [47] d'une lentille mince est la distance algébrique » [45], [48], elle est telle que :
- « pour une lentille convergente » et
- « pour une lentille divergente » ;
les foyers principaux objet et image d'une lentille mince étant géométriquement symétriques relativement au centre optique de cette dernière,
les « distances focale objet et image de la lentille mince sont opposées » c.-à-d. «».
La « vergence d'une lentille mince est définie selon » [49],
elle est exprimée en « dioptries de symbole », les distances focales étant alors en soit «» ;
- si « la lentille est convergente », les foyers principaux objet et image étant « réels » ;
« un faisceau incident divergeant à partir de émerge parallèlement » et
« un faisceau incident converge vers » ; - si « la lentille est divergente », les foyers principaux objet et image étant « virtuels » ;
« un faisceau incident convergeant virtuellement vers situé au-delà de émerge parallèlement » et
« un faisceau incident diverge virtuellement à partir de situé en-deçà de ».
Construction de l'image d'un objet linéique transverse situé à distance finie (ou de l'objet conjugué d'une image linéique transverse située à distance finie) à l'aide de rayons lumineux
[modifier | modifier le wikicode]Construction de l'image d'un objet linéique transverse situé à distance finie à l'aide de rayons lumineux judicieusement choisis
[modifier | modifier le wikicode] Soit « l'objet linéique transverse dont on cherche à déterminer l'image dans les conditions de stigmatisme et d'aplanétisme approchés de la lentille mince », pour faire ceci il suffit de
déterminer « l'image de l'objet »,
déterminer «l'image« le pied de l'image s'obtenant en projetant orthogonalement sur l'axe optique principal » ;
on considère alors « deux rayons incidents issus du point objet parmi les trois particuliers » :
- un rayon incident passant par n'étant pas dévié, le point image appartient réellement ou virtuellement à ce rayon émergent,
- un rayon incident à l'axe optique principal émergeant en passant réellement ou virtuellement par le foyer principal image , le point image appartient réellement ou virtuellement à ce rayon émergent ou
- un rayon incident passant réellement ou virtuellement par le foyer principal objet émergeant parallèlement à l'axe optique principal, le point image appartient réellement ou virtuellement à ce rayon émergent ;
au final le point image est l'intersection des deux rayons émergents « choisis » [50] ;
voir schémas ci-dessous : à gauche, objet réel en deçà du plan focal objet d'une lentille mince convergente, l'image est réelle inversée,
voir schémas ci-dessous : au centre, objet réel entre plan focal objet et face d'entrée d'une lentille mince convergente, l'image est virtuelle droite agrandie [51],
voir schémas ci-dessous : à droite, objet virtuel, l'image par une lentille mince convergente est réelle droite.
-
Construction de l'image par une lentille mince convergente d'un objet linéique transverse situé en deçà du plan focal objet
-
Construction de l'image par une lentille mince convergente d'un objet linéique transverse situé entre le plan focal objet et la face d'entrée
-
Construction de l'image par une lentille mince convergente d'un objet linéique transverse virtuel
-
Construction de l'image par une lentille mince divergente d'un objet linéique transverse réel
-
Construction de l'image par une lentille mince divergente d'un objet linéique transverse virtuel situé entre la face de sortie et le plan focal objet
-
Construction de l'image par une lentille mince divergente d'un objet linéique transverse virtuel situé au-delà du plan focal objet
voir schémas ci-dessus : à gauche, objet réel, l'image par une lentille mince divergente est virtuelle droite,
voir schémas ci-dessus : au centre, objet virtuel entre face de sortie et plan focal objet d'une lentille mince divergente, l'image est réelle droite agrandie,
voir schémas ci-dessus : à droite, objet virtuel au-delà du plan focal objet d'une lentille mince divergente, l'image est virtuelle inversée.
Construction de l'objet conjugué d'une image linéique transverse située à distance finie à l'aide de rayons lumineux judicieusement choisis
[modifier | modifier le wikicode] Soit « l'image linéique transverse dont on cherche à déterminer l'objet conjugué dans les conditions de stigmatisme et d'aplanétisme approchés de la lentille mince », pour faire ceci il suffit
de déterminer « l'objet conjugué de l'image »,
de déterminer « le pied de l'objet s'obtenant en projetant orthogonalement sur l'axe optique principal » ;
on considère alors « deux rayons émergents passant par le point image parmi les trois particuliers » :
- un rayon émergent passant par provenant d'un rayon incident non dévié, le point objet appartient réellement ou virtuellement à ce rayon incident,
- un rayon émergent à l'axe optique principal correspondant à un incident passant réellement ou virtuellement par le foyer principal objet , le point objet appartient réellement ou virtuellement à ce rayon incident ou
- un rayon émergent passant réellement ou virtuellement par le foyer principal image correspondant à un incident à l'axe optique principal , le point objet appartient réellement ou virtuellement à ce rayon incident ;
au final le point objet est l'intersection des deux rayons émergents « choisis » [50] ;
Construction de l'image d'un objet linéique transverse situé à distance infinie ou dans le plan focal objet
[modifier | modifier le wikicode]Construction de l'image d'un objet linéique transverse situé à l'infini et tracés des pinceaux émergents associés aux pinceaux incidents parallèles
[modifier | modifier le wikicode] Soit « l'objet linéique transverse à l'infini dont on cherche l'image par une lentille mince, étant le point à l'infini de l'axe optique principal de cette dernière » ;
« l'image de étant le foyer principal image » et
la lentille étant aplanétique approchée, l'image de est dans le plan focal image de la lentille, par suite
la lentille étant aplanétique ( approchée ),« l'image de est le foyer secondaire image associé à l'axe optique secondaire », c.-à-d. que
la lentille étant aplanétique ( approchée ),« l'image de est » ;
il suffit alors de déterminer « le foyer secondaire image associé à l'axe optique secondaire »,
il suffit alors de déterminer les pinceaux émergents correspondant aux pinceaux issus de convergeant en et
il suffit alors de déterminer les pinceaux émergentsceux correspondant aux pinceaux issus de convergeant en ;
voir schémas ci-dessous : à gauche l'image de l'objet réel [52] par une lentille convergente, l'image est réelle inversée dans le plan focal image,
voir schémas ci-dessous : à droite l'image de l'objet réel [52] par une lentille divergente, l'image est virtuelle droite dans le plan focal image.
-
Construction de l'image, par une lentille mince convergente, d'un objet linéique transverse situé à l'infini
-
Construction de l'image, par une lentille mince divergente, d'un objet linéique transverse situé à l'infini
Construction de l'image d'un objet linéique transverse situé dans le plan focal objet et tracé du cheminement des pinceaux
[modifier | modifier le wikicode] Soit « l'objet linéique transverse dans le plan focal objet dont on cherche l'image par une lentille mince, étant le point de l'axe optique principal de cette dernière » ;
« coïncidant avec le foyer principal objet », « son image est le point à l'infini de l'axe optique principal » et
la lentille étant aplanétique approchée, l'image de est dans le plan focal image de la lentille, par suite
la lentille étant aplanétique ( approchée ),« l'image de coïncide avec le foyer secondaire image associé à l'axe optique secondaire », c.-à-d. que
la lentille étant aplanétique ( approchée ),« l'image de est » ;
il suffit alors de déterminer « l'axe optique secondaire associé au foyer secondaire objet »,
il suffit alors de déterminer les pinceaux émergents correspondant aux pinceaux incidents issus de émergeant à l'axe optique principal et
il suffit alors de déterminer les pinceaux émergentsceux correspondant aux pinceaux incidents issus de émergeant à l'axe optique secondaire ;
voir schémas ci-dessous : à gauche l'image de l'objet réel dans le plan focal objet d'une lentille convergente, l'image est réelle [53] inversée à l'infini,
voir schémas ci-dessous : à droite l'image de l'objet virtuel dans le plan focal objet d'une lentille divergente, l'image est réelle [54] droite à l'infini.
-
Construction de l'image, par une lentille mince convergente, d'un objet linéique transverse réel situé dans le plan focal objet
-
Construction de l'image, par une lentille mince divergente, d'un objet linéique transverse virtuel situé dans le plan focal objet
Construction de l'image d'un objet ponctuel situé sur l'axe optique principal à distance finie (ou de l'objet conjugué d'une image ponctuelle située sur l'axe optique principal à distance finie) par utilisation de la notion de foyers secondaires
[modifier | modifier le wikicode]Construction de l'image d'un objet ponctuel situé sur l'axe optique principal à distance finie par utilisation des foyers secondaires
[modifier | modifier le wikicode] Soit « un objet ponctuel de l'axe optique principal d'une lentille mince » par laquelle on cherche à déterminer l'image , avec l'objet ponctuel à distance finie sur [55], la lentille étant stigmatique approché il suffit de
« choisir un rayon incident paraxial passant par » et de
« déterminer le rayon émergent correspondant »,
ce dernier devant « passer par » d'une part et d'autre part « l'image d'un point de l'axe optique principal étant un point de »,
« est déterminée par l'intersection du rayon émergent avec l'axe optique principal » ;
les rayons incidents les plus pratiques parmi ceux possibles à choisir sont :
- un rayon incident ou son prolongement passant réellement ou virtuellement par coupant le plan focal objet en d'axe optique secondaire associé , support de , émerge, à partir du point d'incidence sur la lentille, parallèlement à ou
- un rayon incident ou son prolongement passant réellement ou virtuellement par , à un axe optique secondaire [56], l'axe optique secondaire coupant le plan focal image de la lentille en , foyer secondaire image associé à , émerge, à partir du point d'incidence sur la lentille, en passant réellement ou virtuellement par ;
voir schémas ci-dessous : à gauche la construction de l'image par une lentille mince convergente d'un objet réel avec utilisation de la notion de foyer secondaire objet,
voir schémas ci-dessous : à droite la construction de l'image par une lentille mince convergente d'un objet réel avec utilisation de la notion de foyer secondaire image.
Construction de l'objet conjugué d'une image ponctuelle située sur l'axe optique principal à distance finie par utilisation des foyers secondaires
[modifier | modifier le wikicode] Soit « une image ponctuelle de l'axe optique principal d'une lentille mince » par laquelle on cherche à déterminer l'objet conjugué , avec l'image ponctuelle à distance finie sur [58], la lentille étant stigmatique approché il suffit de
« choisir un rayon émergent paraxial passant par » et de
« déterminer le rayon incident correspondant »,
ce dernier devant « passer par » d'une part et d'autre part « l'objet conjugué d'un point de l'axe optique principal étant un point de »,
« est déterminée par l'intersection du rayon incident avec l'axe optique principal » ;
les rayons émergents les plus pratiques parmi ceux possibles à choisir sont :
- un rayon émergent ou son prolongement passant réellement ou virtuellement par coupant le plan focal image en d'axe optique secondaire associé , support de , correspond à un incident, en deçà du point d'incidence sur la lentille, à ou
- un rayon émergent ou son prolongement passant réellement ou virtuellement par , à un axe optique secondaire [59], l'axe optique secondaire coupant le plan focal objet de la lentille en , foyer secondaire objet associé à , correspond à un incident, en deçà du point d'incidence sur la lentille, passant réellement ou virtuellement par ;
voir schémas ci-dessous : à gauche la construction de l'objet conjugué par une lentille mince divergente d'une image réelle avec utilisation de la notion de foyer secondaire image,
voir schémas ci-dessous : à droite la construction de l'objet conjugué par une lentille mince divergente d'une image réelle avec utilisation de la notion de foyer secondaire objet.
-
Construction de l'objet conjugué par une lentille mince divergente [57] d'une image ponctuelle réelle par utilisation de la notion de foyer secondaire image
-
Construction de l'objet conjugué par une lentille mince divergente [57] d'une image ponctuelle réelle par utilisation de la notion de foyer secondaire objet
Relations de conjugaison approchée de Descartes et de Newton d'une lentille mince
[modifier | modifier le wikicode]Orientation des espaces objet et image
[modifier | modifier le wikicode]Chaque espace objet ou image est « orienté à droite » [60] avec choix d'une « base commune orthonormée directe » [61] c.-à-d. déterminée par la « règle de la main droite » [62] dont
- « le 1er vecteur est celui orientant l'axe optique principal dans sa partie incidente ou émergente » [63],
- « les 2ème et 3ème orientant les plans transverses objets ou images »,
« le 2ème étant commun aux deux espaces, choisi à l'objet linéique transverse étudié »,
« le 3ème, également commun aux deux espaces, orientant les angles du plan d'incidence et d'émergence ».
Repérage de Descartes des points objet et image
[modifier | modifier le wikicode]L'« origine des abscisses objet et image de Descartes [25] des points de l'axe optique principal d'une lentille mince », étant préalablement algébrisé dans le sens incident de propagation de la lumière, « est commune choisie au centre optique de cette dernière » ;
- un « point objet de l'axe optique principal est repéré par son abscisse objet de Descartes [25] » « pour un objet réel » et « pour un objet virtuel » [64] ;
- un « point image de l'axe optique principal est repéré par son abscisse image de Descartes [25] » « pour une image réelle » et « pour une image virtuelle » [65].
Repérage de Newton des points objet et image
[modifier | modifier le wikicode] L'« origine des abscisses objet et image de Newton [66] des points de l'axe optique principal d'une lentille mince », étant préalablement algébrisé dans le sens incident de propagation de la lumière, « est choisie différemment suivant la nature objet ou image du point à repérer », l'origine étant choisie
L'« origine des abscisses objet et image de Newton au foyer principal objet de la lentille pour un point objet et
L'« origine des abscisses objet et image de Newton au foyer principal image de cette dernière pour un point image ;
- un « point objet de l'axe optique principal est repéré par son abscisse objet de Newton [66] » « pour un objet situé en deçà du foyer principal objet » et « pour un objet situé au-delà du foyer principal objet » [67] ;
- un « point image de l'axe optique principal est repéré par son abscisse image de Newton [66] » « pour une image située au-delà du foyer principal image » et « pour une image située en deçà du foyer principal image » [68].
Relations de conjugaison approchée de Descartes
[modifier | modifier le wikicode]La 1ère relation de conjugaison approchée ou relation de conjugaison approchée de position de Descartes [25] traduit le stigmatisme approché de la lentille mince pour un point objet de l'axe optique principal et
la 2ème relation de conjugaison approchée ou relation de conjugaison approchée de grandissement transverse de Descartes [25] traduit l'aplanétisme approché de cette lentille mince pour un objet linéique transverse .
Première relation de conjugaison (ou relation de conjugaison de position) de Descartes
[modifier | modifier le wikicode]L'application de la relation de conjugaison de position de Descartes [25] au couple conduit à soit «» et
L'application de la relation de conjugaison de position de Descartes au couple conduit à soit «».
Deuxième relation de conjugaison (ou relation de conjugaison de grandissement transverse) de Descartes
[modifier | modifier le wikicode]Rappel de la définition du grandissement transverse d'un objet linéique transverse [70] : étant un objet linéique transverse de pied sur l'axe optique principal d'une lentille mince et son image linéique transverse [71] par cette dernière, on définit la grandissement transverse de l'objet par la lentille selon «».
Si « sont de même signe », le grandissement transverse est « positif », l'image est qualifiée de « droite » [73] et
si « sont de signe contraire », le grandissement transverse est « négatif », l'image est qualifiée d'« inversée » [74].
Relations de conjugaison approchée de Newton
[modifier | modifier le wikicode]Comme pour celles de Descartes [25], la 1ère relation de conjugaison approchée ou relation de conjugaison approchée de position de Newton [66] traduit le stigmatisme approché de la lentille mince pour un point objet de l'axe optique principal et
Comme pour celles de Descartes, la 2ème relation de conjugaison approchée ou relation de conjugaison approchée de grandissement transverse de Newton [66] traduit l'aplanétisme approché de cette lentille mince pour un objet linéique transverse .
Première relation de conjugaison (ou relation de conjugaison de position) de Newton
[modifier | modifier le wikicode] L'application de la relation de conjugaison de position de Newton [66] au point objet « centre optique de la lentille », permet de vérifier la « propriété de point double de ce dernier » car
L'application de la relation de conjugaison de position de Newton l'abscisse objet de Newton [66] de valant «», la 1ère relation de conjugaison de Newton [66]
L'application de la relation de conjugaison de position de Newton l'abscisse image de Newton [66] de l'image de , «» l'« image de est » [77].
Deuxième relation de conjugaison (ou relation de conjugaison de grandissement transverse) de Newton
[modifier | modifier le wikicode]Voir le paragraphe « 2ème relation de conjugaison (ou relation de conjugaison de grandissement transverse) de Descartes (rappel de la définition du grandissement transverse d'un objet linéique transverse) » plus haut dans ce chapitre.
Si « respectivement sont de même signe », le grandissement transverse est « négatif », l'image est qualifiée d'« inversée » [80] et
si « respectivement sont de signe contraire », le grandissement transverse est « positif », l'image est qualifiée de « droite » [81].
Établissement des relations de conjugaison d'une lentille mince à partir de la construction de l'image d'un objet linéique transverse
[modifier | modifier le wikicode]Constructions fondamentales de l'image d'un objet linéique transverse pour démontrer les relations de conjugaison de Descartes et de Newton
[modifier | modifier le wikicode]
le 1er passant par ,
le 2ème à l'axe optique principal et
le 3ème passant par
On construit l'image d'un « objet linéique transverse réel » par une lentille sphérique mince [82] « convergente » [83] dans le cas où « l'image est réelle » [84] en utilisant trois rayons incidents issus de :
- un 1er représenté par passant par le centre optique , n'est pas dévié son émergent est aussi représenté par ,
- un 2nd représenté par à l'axe optique principal, émerge par le point d'incidence sur la lentille en passant par le foyer principal image cet émergent est aussi représenté par et
- un 3ème représenté par passant par le foyer principal objet , émerge par le point d'incidence sur la lentille parallèlement à l'axe optique principal cet émergent est aussi représenté par ;
le point image , conjugué de par la lentille, est alors à l'intersection des trois rayons émergents, s'obtenant en projetant orthogonalement sur l'axe optique principal de cette dernière.
Démonstration des trois relations de conjugaison de grandissement transverse de Descartes et de Newton
[modifier | modifier le wikicode]On utilise la similitude de triangles ayant pour sommet commun respectivement , et ;
- on évalue la valeur absolue du grandissement transverse par «similitude des triangles et » soit «» et on détermine le signe en passant aux mesures algébriques d'où «» en effet sur la figure , , et soit finalement « la relation de conjugaison de grandissement transverse de Descartes » [25] «» ;
- on évalue la valeur absolue du grandissement transverse par similitude des triangles « et » soit, avec «, » et on détermine le signe en passant aux mesures algébriques d'où «» en effet sur la figure , , et soit finalement « une des deux relations de conjugaison de grandissement transverse de Newton » [66] «» ;
- on évalue la valeur absolue du grandissement transverse par similitude des triangles « et » soit, avec «, » et on détermine le signe en passant aux mesures algébriques d'où «» en effet sur la figure , , et soit finalement « l'autre des deux relations de conjugaison de grandissement transverse de Newton » [66] «».
Démonstration des deux relations de conjugaison de position de Descartes et de Newton
[modifier | modifier le wikicode]Introduction : On se sert des relations de conjugaison de grandissement transverse déterminées précédemment voir le paragraphe « démonstration des trois relations de conjugaison de grandissement transverse de Descartes et de Newton » [85] plus haut dans ce chapitre.
Démonstration de la relation de conjugaison de position de Newton [66] : on égale les deux expressions de grandissement transverse de Newton [66] d'où «» et par « égalité des produits des extrêmes et des moyens » [86] on obtient « la relation de conjugaison de position de Newton » [66]
Démonstration de la relation de conjugaison de position de Descartes [25] : on égale une des expressions de grandissement transverse de Newton [66], par exemple «»,
Démonstration de la relation de conjugaison de position de Descartes : on égale à celle de Descartes [25] «» d'où «», puis
Démonstration de la relation de conjugaison de position de Descartes : on fait le changement d'origine sur l'abscisse de Newton [66] de de façon à ne conserver que le repérage de Descartes [25] « » ce qui donne «» ou encore «» et,
Démonstration de la relation de conjugaison de position de Descartes : en divisant de part et d'autre par , la relation «» c.-à-d.
Démonstration de la relation de conjugaison de position de Descartes : en divisant de part et d'autre par , « la relation de conjugaison de position de Descartes » [25]
Grandissement angulaire d'un pinceau lumineux, relation de Lagrange-Helmholtz
[modifier | modifier le wikicode]Expression de Descartes du grandissement angulaire d'un pinceau lumineux issu d'un point objet de l'axe optique principal
[modifier | modifier le wikicode]
On considère un pinceau lumineux issu du point objet [87] de direction d'abscisse angulaire «» où est l'axe optique principal orienté dans le sens de la propagation et le point d'incidence du rayon moyen du pinceau sur la lentille, le pinceau émergent correspondant passant par [88] de direction d'abscisse angulaire définie par «» [89] voir schéma ci-contre ;
le grandissement angulaire du pinceau issu de voir le paragraphe « définition du grandissement angulaire d'un pinceau lumineux issu d'un point objet » du chap. de la leçon « Signaux physiques (PCSI) » se définit selon
- Pour évaluer , on explicite puis on algébrise en utilisant le schéma , et soit et enfin on utilise une « condition de Gauss de stigmatisme approché » d'où «» et par suite «» ;
- pour évaluer , on explicite puis on algébrise en utilisant le schéma , et soit et enfin on utilise une « conséquence des deux conditions de Gauss de stigmatisme [89] » d'où «» et par suite «» ;
- on en déduit le grandissement angulaire «» donnant, après simplification, «» d'où l'expression de Descartes [25] du grandissement angulaire «» [90].
Relation de Lagrange-Helmholtz d'une lentille (sphérique) mince
[modifier | modifier le wikicode]La « relation de Lagrange - Hemholtz » [91], [92] est le lien entre le grandissement transverse d'un objet linéique transverse et le grandissement angulaire d'un pinceau issu du point objet ;
la relation de conjugaison de grandissement transverse de Descartes [25] pour une lentille mince étant «» et l'expression de Descartes [25] du grandissement angulaire pour la même lentille mince «» on en déduit aisément la « relation de Lagrange - Helmholtz » [91], [92] d'une lentille sphérique mince
Conditions de Bessel séparant un objet linéique transverse réel et son image par une lentille mince convergente pour que l'image soit réelle
[modifier | modifier le wikicode]Position du problème
[modifier | modifier le wikicode]On veut projeter l'image d'un objet « rétroéclairé » [94] sur un écran de façon à obtenir une image agrandie tout en restant aussi lumineuse et nette que possible, avec une distance entre l'objet et l'écran imposée par les conditions extérieures.
Nécessité de choix d'une lentille convergente
[modifier | modifier le wikicode]L'objet étant réel et l'image devant être réelle, la seule possibilité est une lentille « convergente » [95] séparée de l'objet d'une « distance supérieure à la distance focale de la lentille » d'où le choix de nécessairement inférieure à la distance entre l'écran et l'objet [96].
« Condition de Bessel » du choix de lentille pour avoir une image nette sur l'écran
[modifier | modifier le wikicode]La distanceentre l'objet et l'écran étant imposée comment choisir la distance focale de la lentille et où la placer c.-à-d. où placer son centre optique ?

On cherche simultanément la « distance focale de la lentille mince convergente » et
On cherche simultanément « la distance séparant celle-ci de l'objet » et pour cela
on va écrire que les plans de front contenant l'objet et l'écran sont conjugués avec, pour
on va écrire « abscisse de Descartes [25] de l'objet » et
on va écrire « celle de Descartes [25] de l'image » d'où
on va écrire par 1ère relation de conjugaison de Descartes [25] «» [97], équation algébrique en paramétrée par , que l'on peut réécrire selon «» ou «» soit enfin
on va écrire l'équation du 2ème degré en «» ;
cette équation admet des solutions réelles si son discriminant est positif soit «» ou «» nécessitant que
avec le choix nécessaire «», la distance séparant la lentille de l'objet :
- est « unique si » distance de Silbermann [99], correspondant à «», sa valeur étant «»,
- a « deux valeurs si » distances de Bessel [98], correspondant à «», ses valeurs étant «» et «»ces deux positions de lentilles sont symétriques par rapport à c.-à-d. l'abscisse du plan séparant l'espace entre le plan objet et l'écran en deux sous-espaces d'expansion tridimensionnelle géométriquement identique.
l'une ou l'autre des valeurs constituant la 1ère condition de Bessel [98] pour avoir une image nette sur l'écran ;
« Condition de Bessel » du choix de la position de la lentille pour avoir un grandissement transverse suffisant
[modifier | modifier le wikicode] Remarquons d'abord que si « la distance séparant l'objet de la lentille est »,
Remarquons d'abord que si « celle séparant la lentille de l'écran est » et vice-versa ;
Remarquons le grandissement transverse vaut donc :
- si « la distance séparant l'objet de la lentille est », «» soit encore «» de valeur absolue «»,
- si « la distance séparant l'objet de la lentille est », «» soit encore «» de valeur absolue «», avec « » ;
on constate que les grandissements transverses tous deux négatifs correspondent à une image inversée ;
« la position de lentille donnant le plus grand grandissement transverse en valeur absolue est celle correspondant à la plus petite distance séparant la lentille de l'objet soit », ce choix définissant la 2ème condition de Bessel [98] pour avoir un grandissement transverse suffisant, ce dernier en valeur absolue étant égal à «».
Remarques : Vérifiant que « est une fonction de à fixée » [100], il faut donc choisir assez éloigné de par valeur inférieure pour avoir un grandissement suffisant ;
Remarques : vérifiant que « est une fonction de à fixée » [101], nous en déduisons, dans la mesure où on travaille avec une lentille de distance focale fixée, qu'il faut choisir une distance assez éloignée de par valeur supérieure pour avoir un grandissement suffisant.
Remarques : Si on choisit la distance de Silbermann [99] «», la lentille étant au milieu de l'espace séparant l'objet de l'écran, «» et «» d'où un grandissement transverse égal à «», l'image étant alors de même taille que l'objet mais inversée, nous sommes loin du but recherché.
Prise en compte des conditions de Gauss
[modifier | modifier le wikicode]Pour que l'image soit suffisamment nette les conditions de stigmatisme et d'aplanétisme de Gauss [2] doivent être respectées
pour que l'image soit suffisamment grande la 2ème condition de Bessel [98] précise qu'il faut choisir
- d'une part la position de Bessel [98] la plus proche de l'objet pour avoir la valeur absolue du grandissement transverse soit la plus grande des deux avec
- d'autre part aussi petit que possible pour que le grandissement transverse en valeur absolue soit suffisamment grand ;
or le choix de aussi petit que possible pour « réaliser au mieux la 2ème partie de la 2ème condition de Bessel [98] » entraîne
- un rapprochement de la lentille de l'objet en effet « si à fixée » et par suite
- une augmentation de l'angle sous lequel l'objet est vu du centre optique donc « une moins bonne réalisation de la condition d'aplanétisme approché de Gauss » [2] simultanément à
- une augmentation de l'inclinaison des rayons issus des point objets donc « une moins bonne réalisation de l'une des conditions de stigmatisme approché de Gauss » [2] on peut toutefois limiter l'augmentation de l'inclinaison des rayons issus des point objets par utilisation d'un diaphragme placé légèrement avant la lentille.
En conclusion il y a un compromis à trouver entre une taille d'image suffisamment grande nécessitant de « diminuer la focale » de la lentille et une image suffisamment nette qui requiert d'« augmenter sa focale » pour éloigner la lentille de l'objet.
Éclairage de l'objet
[modifier | modifier le wikicode]
L'objet est éclairé de façon optimale si tous les rayons provenant de l'objet traverse la lentille de projection et pour que ceci soit réalisé il convient d'utiliser une lanterne munie d'un « condenseur » pour éclairer l'objet.
Définition d'un condenseur : un condenseur est souvent formé de l’association de deux lentilles plan convexes dont les faces bombées sont en regard, la distance focale habituelle est de l’ordre de ;
Définition d'un condenseur : souvent utilisé hors conditions de Gauss, le but n'étant pas de former une image, il n’a pas besoin d’être de grande qualité optique, on lui demande seulement d’être de grande dimension car c’est ce qui limite la taille de l’objet projetable, et d’être assez convergent, pour des problèmes d’encombrement.
En effet un montage sommaire conduirait à la situation ci-contre, la lentille de projection ne recevant qu'une petite partie de la lumière qui traverse l'objet, la partie visible de l'objet serait fortement réduite.

Pour y remédier on place donc un « condenseur » entre la lanterne et l'objet ce qui conduit à la situation ci-contre à gauche, la lentille de projection « recevant ainsi toute la lumière qui a traversé l'objet ».
Réglage d'un condenseur : L'idéal est de « placer le condenseur de façon à ce que l'image du filament de la lampe par le condenseur se fasse sur la lentille de projection », cette dernière donnant alors une image de cette image de filament également confondue sur la lentille et par suite ne se retrouvant pas au-delà de la lentille ou
Réglage d'un condenseur : L'idéal est de faire, comme sur le schéma ci-contre à gauche, l'image du filament légèrement au-delà de la lentille de projection, de façon à ce que l'image qu'en donnera la lentille de projection soit certes réelle l'image de filament jouant le rôle d'objet virtuel pour cette lentille de projection, son image sera réelle mais rapprochée de la lentille de projection donc ne risquant pas de se retrouver sur l'écran.
Modélisation d'un dispositif dioptrique d'utilisation courante à l'aide de plusieurs lentilles minces en série
[modifier | modifier le wikicode]Introduction, réglage pour une observation par un œil n'accommodant pas
[modifier | modifier le wikicode]L'œil sera étudié de façon plus approfondie au chapitre suivant mais dès à présent il faut savoir modéliser un œil par une « lentille de vergence variable, le cristallin » et par un « écran, la rétine », cette dernière restant à distance constante du cristallin ; par contraction plus ou moins grande, le cristallin réalise la conjugaison d'un plan de front situé à la distance de l'œil avec la rétine :
- quand le cristallin ne se contracte pas, on dit que « l’œil n'accommode pas », la distance est alors infinie pour un œil « normal » et le plan de front est au « punctum remotum » de l'œil,
- quand le cristallin se contracte au maximum, on dit que « l’œil accommode au maximum », la distance est alors de pour un œil « normal » et le plan de front est au « punctum proximum » de l'œil ;
pour un minimum de fatigue visuelle il convient de faire les réglages des dispositifs dioptriques d'utilisation courante de façon à ce que l'œil de l'observateur n'accommode pas et par suite l'image d'un objet observé à travers un dispositif dioptrique doit être à l'infini, cette image servant d'objet pour l'œil de l'observateur, ce dernier donnera une image définitive localisée sur la rétine donc visuellement nette.
Lunette de Galilée
[modifier | modifier le wikicode]Lunette la plus simple permettant d'observer des objets terrestres situés à grande distance donc considérés comme localisés à l'infini ; on modélise la lunette par deux lentilles minces :
- l'une appelée « objectif » située du côté de l'objet observé et par laquelle la lumière provenant de cet objet entrera cette lentille jouera donc le rôle de « face d'entrée » convergente à grande focale dans le cas de la lunette de Galilée [102], exemple ,
- l'autre appelée « oculaire » située du côté de l'œil de l'observateur et par laquelle la lumière sortira pour ensuite pénétrer dans l'œil cette lentille jouera donc le rôle de « face de sortie » divergente à petite focale en valeur absolue dans le cas de la lunette de Galilée, exemple .
Nécessité du caractère afocal de la lunette et conséquence sur la disposition des deux lentilles
[modifier | modifier le wikicode]Un objet à l'infini de l'axe optique principal devant être conjugué par la lunette d'une image à l'infini de , la « lunette de Galilée doit être afocale » ; on a donc,
- en partant de l'objet observé situé à l'infini, la conjugaison par l'objectif «» et,
- en partant de l'image finale également à l'infini, la conjugaison par l'oculaire «»
donnant globalement «» dans la mesure où
« le plan focal image de l'objectif est confondu avec le plan focal objet de l'oculaire »
condition pour qu'un doublet de lentilles soit afocal.
Conséquence sur l'encombrement de la lunette
[modifier | modifier le wikicode]L'encombrement de la lunette est défini comme la distance séparant la face d'entrée de la lunette de celle de sortie soit « » [103] ou «» [104]
Tracé de l'image d'un objet linéique transverse et cheminement des pinceaux parallèles issus des points extrêmes de l'objet
[modifier | modifier le wikicode]-
Cheminement, à travers une lunette de Galilée, de pinceaux lumineux issus des extrémités d'un objet linéique transverse à l'infini schéma hors échelle
On sait que «» pour le point objet à l'infini sur l'axe optique principal donnant au final le point image à l'infini de l'axe optique principal et
On sait que «» pour le point objet à l'infini de l'axe optique secondaire de l'objectif étant l'autre extrémité de l'objet linéique transverse à l'infini , ce point objet à l'infini donnant au final le point image à l'infini de l'axe optique secondaire de l'oculaire [106] d'où le schéma ci-dessus :
Définition du grossissement de la lunette de Galilée et son évaluation
[modifier | modifier le wikicode]« étant l'angle algébrisé sous lequel l'observateur voit l'objet à travers la lunette » et « l'angle algébrisé sous lequel il le voit à l'œil nu »,
son évaluation se fait par l'intermédiaire de la « tangente des angles » [109] dans les triangles rectangles faisant intervenir la hauteur algébrisée de l'image intermédiaire «» sur le schéma du paragraphe « tracé de l'image d'un objet linéique transverse et cheminement des pinceaux parallèles issus des points extrêmes de l'objet » plus haut dans ce chapitre à savoir les triangles «» et «» :
- « dans le triangle rectangle » on a «» [110] ou, avec , l'évaluation «» ;
- « dans le triangle rectangle » on a «» [111] ou, avec , l'évaluation «» ;
faisant le rapport nous en déduisons le grossissement cherché «» et, utilisant , nous obtenons
Définition du cercle oculaire, établissement de sa position et de sa taille
[modifier | modifier le wikicode] Tous les rayons pénétrant dans la lunette traversent inévitablement sa face d'entrée c.-à-d. l'objectif de la lunette, ils sortiront de la lunette en passant nécessairement par l'image de l'objectif par la lunette ;
sachant que «» on constate que « l'image de l'objectif par la lunette est aussi l'image de l'objectif par l'oculaire » d'où la définition du « cercle oculaire » ci-dessous et sa conséquence sur la traversée des rayons.
Définition du cercle oculaire de la lunette et propriétés des rayons traversant la lunette
[modifier | modifier le wikicode]« Le cercle oculaire de la lunette est l'image de l'objectif par l'oculaire » ;
« tous les rayons pénétrant dans la lunette ressortent en traversant le cercle oculaire » et
comme ce dernier est aussi l'endroit de « resserrement maximal autour de l'axe optique principal des rayons émergents » propriété admise, c'est sur le cercle oculaire que l'éclairement est maximal,
c'est donc sur le cercle oculaire qu'il serait préférable de positionner l'œil de l'observateur à condition toutefois que ce soit possible c.-à-d. que le cercle oculaire soit réel et non virtuel [114]
Position du centre du cercle oculaire
[modifier | modifier le wikicode]
Notant « le centre du cercle oculaire », c.-à-d. le conjugué du centre optique de l'objectif par l'oculaire «», on obtient
Notant sa position en utilisant l'une des relations de conjugaison de position de Descartes [25] ou de Newton [66],
Notant par exemple celle de Newton [66] avec «» [115] soit «» et «» déterminée par «» [116]
Notant d'où «» positionnant le centre du cercle oculaire relativement au foyer principal image de l'oculaire soit
« le centre du cercle oculaire se trouve légèrement au-delà du foyer principal image de l'oculaire, à au-delà de », il est donc virtuel « pratiquement confondu avec », plus exactement « en » soit finalement «» et l'observateur ne pourra pas y positionner son œil [114] !
Taille du cercle oculaire pour un objectif de taille précisée
[modifier | modifier le wikicode]Pour déterminer la taille du cercle oculaire il suffit d'évaluer « le grandissement transverse par l'oculaire de l'objet linéique transverse », étant le bord « supérieur » de l'objectif dans le plan d'incidence contenant l'axe optique principal de la lunette de Galilée [102] et au vecteur unitaire voir le schéma de positionnement du cercle oculaire et des rayons extrêmes traversant l'objectif plus bas dans ce chapitre, « étant l'image correspondante par l'oculaire » le grandissement transverse par l'oculaire de l'objet linéique transverse valant,
d'où «» dont on déduit la taille de l'image linéique transverse
ce qui donne, pour un objectif de de diamètre ou de rayon un cercle oculaire virtuel de « de rayon »,
Schéma de positionnement du cercle oculaire et des rayons extrêmes traversant l'objectif
[modifier | modifier le wikicode]
Voir ci-contre :
Inconvénient de la lunette de Galilée
[modifier | modifier le wikicode]Le cercle oculaire étant virtuel il y a impossibilité d'y positionner l'œil, il faut donc le mettre dans l'espace image réelle de la lunette de Galilée [102] au plus près de sa face de sortie c.-à-d. l'oculaire [114] mais
Le cercle oculaire étant virtuel il y a nécessairement perte de puissance lumineuse moyenne car c'est alors la « pupille de l'œil » [118] qui la limite, celle-ci étant certainement de diamètre inférieur à celui de l'oculaire
Avantage de la lunette de Galilée
[modifier | modifier le wikicode] Relativement à la « lunette astronomique » étudiée plus bas dans ce chapitre : L'encombrement est moins grand et
Relativement à la « lunette astronomique » étudiée plus bas dans ce chapitre : l'image est droite ce qui est utile lorsque l'on fait une observation terrestre pour des objets éloignés bien sûr mais
Relativement à la « lunette astronomique » étudiée plus bas dans ce chapitre : l'image est droite ce qui n'est pas indispensable pour une observation céleste.
Lunette astronomique
[modifier | modifier le wikicode]Lunette permettant d'observer des objets célestes situés à très grande distance donc considérés comme localisés à l'infini ; on modélise la lunette par deux lentilles minces :
- l'une appelée « objectif » située du côté de l'objet observé et par laquelle la lumière provenant de cet objet entrera cette lentille jouera donc le rôle de « face d'entrée » convergente à grande focale dans le cas de la lunette astronomique, exemple ,
- l'autre appelée « oculaire » située du côté de l'œil de l'observateur et par laquelle la lumière sortira pour ensuite pénétrer dans l'œil cette lentille jouera donc le rôle de « face de sortie » également convergente à petite focale dans le cas de la lunette astronomique, exemple .
Nécessité du caractère afocal de la lunette et conséquence sur la disposition des deux lentilles
[modifier | modifier le wikicode] Un objet à l'infini de l'axe optique principal devant être conjugué par la lunette d'une image à l'infini de pour un œil n'accommodant pas, la « lunette astronomique doit être afocale » ;
on a donc,
- en partant de l'objet observé situé à l'infini, la conjugaison par l'objectif «» et,
- en partant de l'image finale également à l'infini, la conjugaison par l'oculaire «»
donnant globalement «» dans la mesure où
« le plan focal image de l'objectif est confondu avec le plan focal objet de l'oculaire »
condition pour qu'un doublet de lentilles soit afocal.
Conséquence sur l'encombrement de la lunette
[modifier | modifier le wikicode]L'encombrement de la lunette est défini comme la distance séparant la face d'entrée de la lunette de celle de sortie soit « » [103] ou «» [104]
Tracé de l'image d'un objet linéique transverse et cheminement des pinceaux parallèles issus des points extrêmes de l'objet
[modifier | modifier le wikicode]-
Cheminement, à travers une lunette astronomique, de pinceaux lumineux issus des extrémités d'un objet linéique transverse à l'infini schéma hors échelle
On sait que «» pour le point objet à l'infini sur l'axe optique principal donnant au final le point image à l'infini de l'axe optique principal et
On sait que «» pour le point objet à l'infini de l'axe optique secondaire de l'objectif étant l'autre extrémité de l'objet linéique transverse à l'infini , ce point objet à l'infini donnant au final le point image à l'infini de l'axe optique secondaire de l'oculaire [106] d'où le schéma ci-dessus :
Remarque : Contrairement au résultat obtenu avec une lunette de Galilée, l'image par une lunette astronomique est inversée [120].
Définition du grossissement de la lunette astronomique et son évaluation
[modifier | modifier le wikicode]« étant l'angle algébrisé sous lequel l'observateur voit l'objet à travers la lunette » et « l'angle algébrisé sous lequel il le voit à l'œil nu »,
son évaluation se fait par l'intermédiaire de la « tangente des angles » [109] dans les triangles rectangles faisant intervenir la hauteur algébrisée de l'image intermédiaire «» sur le schéma du paragraphe « tracé de l'image d'un objet linéique transverse et cheminement des pinceaux parallèles issus des points extrêmes de l'objet » plus haut dans ce chapitre à savoir les triangles «» et «» :
- « dans le triangle rectangle » on a «» [110] ou, avec , l'évaluation «» ;
- « dans le triangle rectangle » on a «» [121] ou, avec , l'évaluation «» ;
faisant le rapport nous en déduisons le grossissement cherché «» et, utilisant , nous obtenons
Définition du cercle oculaire, établissement de sa position et de sa taille
[modifier | modifier le wikicode]Voir aussi le sous paragraphe « définition du cercle oculaire, établissement de sa position et de sa taille » du paragraphe « lunette de Galilée » [102] plus haut dans ce chapitre, nous rappelons ci-dessous les résultats justifiant la définition du cercle oculaire :
Tous les rayons pénétrant dans la lunette traversent inévitablement sa face d'entrée c.-à-d. l'objectif de la lunette, ils sortiront de la lunette en passant nécessairement par l'image de l'objectif par la lunette ;
sachant que «» on constate que « l'image de l'objectif par la lunette est aussi l'image de l'objectif par l'oculaire » d'où la définition du « cercle oculaire » ci-dessous et sa conséquence sur la traversée des rayons.
« tous les rayons pénétrant dans la lunette ressortent en traversant le cercle oculaire » et
comme ce dernier est aussi l'endroit de « resserrement maximal autour de l'axe optique principal des rayons émergents » propriété admise, c'est sur le cercle oculaire que l'éclairement est maximal,
c'est donc sur le cercle oculaire qu'il serait préférable de positionner l'œil de l'observateur à condition toutefois que ce soit possible c.-à-d. que le cercle oculaire soit réel et non virtuel [114]
Position du centre du cercle oculaire
[modifier | modifier le wikicode]
Notant « le centre du cercle oculaire », c.-à-d. le conjugué du centre optique de l'objectif par l'oculaire «», on obtient
Notant sa position en utilisant l'une des relations de conjugaison de position de Descartes [25] ou de Newton [66],
Notant par exemple celle de Newton [66] avec «» [115] soit «» et «» déterminée par «» [116]
Notant d'où «» positionnant le centre du cercle oculaire relativement au foyer principal image de l'oculaire soit
« le centre du cercle oculaire se trouve légèrement au-delà du foyer principal image de l'oculaire, à au-delà de », il est donc réel « pratiquement confondu avec », plus exactement « en » soit finalement «» et l'observateur y positionne son œil.
Taille du cercle oculaire pour un objectif de taille précisée
[modifier | modifier le wikicode]Pour déterminer la taille du cercle oculaire il suffit d'évaluer « le grandissement transverse par l'oculaire de l'objet linéique transverse », étant le bord « supérieur » de l'objectif dans le plan d'incidence contenant l'axe optique principal de la lunette astronomique et au vecteur unitaire voir le schéma de positionnement du cercle oculaire et des rayons extrêmes traversant l'objectif plus bas dans ce chapitre, « étant l'image correspondante par l'oculaire » le grandissement transverse par l'oculaire de l'objet linéique transverse valant,
d'où «» dont on déduit la taille de l'image linéique transverse
ou, en valeur absolue «»
ce qui donne, pour un objectif de de diamètre ou de rayon un cercle oculaire réel de « de rayon »,
Schéma de positionnement du cercle oculaire et des rayons extrêmes traversant l'objectif
[modifier | modifier le wikicode]
Voir ci-contre :
Avantage de la lunette astronomique (relativement à la lunette de Galilée)
[modifier | modifier le wikicode] Le cercle oculaire étant réel il y a possibilité d'y positionner l'œil et c'est ce qui est effectivement fait
la taille du cercle oculaire étant de même ordre de grandeur que le diamètre de la pupille de l'œil dans l'obscurité [118] ce qui représente effectivement les conditions d'observation du ciel nocturne pas de perte de puissance lumineuse moyenne !
« Inconvénient » de la lunette astronomique
[modifier | modifier le wikicode]L'image est inversée [120] !
Microscope
[modifier | modifier le wikicode]Appareil dioptrique permettant d'observer des objets de très petites dimensions « localisés à distance finie » avec un grand grossissement représentant le facteur multiplicatif de l'angle sous lequel on voit l'objet à travers le microscope relativement à l'angle sous lequel on voit l'objet directement[123] on modélise le microscope par deux lentilles minces :
- l'une appelée « objectif » située du côté de l'objet observé et par laquelle la lumière provenant de cet objet entrera cette lentille jouera donc le rôle de « face d'entrée » convergente à très petite focale, exemple ,
- l'autre appelée « oculaire » située du côté de l'œil de l'observateur et par laquelle la lumière sortira pour ensuite pénétrer dans l'œil cette lentille jouera donc le rôle de « face de sortie » convergente également à petite focale, exemple .
Caractère focal du microscope, notion d'intervalle optique et ordre de grandeur de sa valeur pour avoir un fort grossissement
[modifier | modifier le wikicode]Un objet à distance finie de l'axe optique principal devant être conjugué par le microscope d'une image à l'infini sur pour un œil n'accommodant pas, le « microscope est focal » ;
l'endroit de l'axe optique principal où il faut centrer le petit objet à visualiser devant être le conjugué, par le microscope et pour un œil n'accommodant pas, du point image à l'infini sur , est
le « foyer principal objet du microscope » c.-à-d. tel que «» ou,
le « foyer principal objet Fo du microscope » en le définissant relativement aux lentilles composant le microscope «» [124] d'où
le « foyer principal objet Fo du microscope » le foyer principal objet du microscope est l'antécédent par l'objectif du foyer principal objet de l'oculaire
on définit « l'intervalle optique du microscope » comme la « distance séparant le foyer principal image de l'objectif du foyer principal objet de l'oculaire » c.-à-d. «» [125] ;
l'intervalle optique doit être choisi grand relativement à la distance focale de l'objectif pour que le grossissement du microscope soit grand en valeur absolue [126], exemple «».
Conséquence sur l'encombrement du microscope
[modifier | modifier le wikicode]L'encombrement du microscope est défini comme la distance séparant la face d'entrée du microscope de celle de sortie soit « » s'écrivant encore « » [104]
donnant numériquement «».
Tracé de l'image d'un objet linéique transverse et cheminement des pinceaux parallèles issus des points extrêmes de l'objet
[modifier | modifier le wikicode]-
Cheminement, à travers un microscope, de pinceaux lumineux issus des extrémités d'un objet linéique transverse réel à distance finie donnant des pinceaux émergents schéma hors échelle
On sait que point objet de l'axe optique principal doit avoir pour conjugué, par le microscope, le point à l'infini de l'œil n'accommodant pas soit «» [124] et
On sait que le point objet , autre extrémité de l'objet linéique transverse , a pour conjugué le point image à l'infini sur l'axe optique secondaire de l'oculaire [127] c.-à-d. «» [128],
l'objet linéique transverse réel donnant par l'objectif une image intermédiaire réelle « quasi à l'infini de l'objectif car », ce qui nécessite que l'objet soit positionné légèrement en deçà du plan focal objet de l'objectif, d'où le schéma ci-dessus.
Définition du grossissement commercial du microscope et son évaluation
[modifier | modifier le wikicode]
Le grossissement du microscope nécessite une définition autre que celle utilisée pour une lunette afocale car l'objet ici étant de petites dimensions ne serait pas visible directement avec un œil n'accommodant pas, un objet de petites dimensions placé à l'infini étant quasi ponctuel !
Il faut donc préciser la manière dont l'objet est vu à l'œil nu avant de le comparer à son observation à travers le microscope et pour cela il y a « plusieurs façons » mais une seule est indépendante des caractéristiques géométriques du microscope, son choix aboutissant à la définition du grossissement dit « commercial » [129] :
« l'angle algébrisé sous lequel il le voit à l'œil nu quand il le place dans le même sens au punctum proximum de son œil » [130] c.-à-d.
dans le même sens à la distance [131] d'un œil « normal ».
Son évaluation se fait par l'intermédiaire de la « tangente des angles » [109] dans le triangle rectangle faisant intervenir la hauteur algébrisée de l'image intermédiaire «» sur le schéma du paragraphe « tracé de l'image d'un objet linéique transverse et cheminement des pinceaux parallèles issus des points extrêmes de l'objet » plus haut dans ce chapitre à savoir le triangle «» et aussi dans le triangle rectangle d'observation directe de l'objet faisant intervenir la hauteur algébrisée de l'objet «» sur le schéma ci-dessus à savoir le triangle «» dans lequel est la position de l'œil :
- « dans le triangle rectangle » on a «» [121] ou, avec , l'évaluation «» ;
- « dans le triangle rectangle » on a «» [132] ou, avec , l'évaluation «» ;
faisant le rapport nous en déduisons le grossissement commercial cherché «» et,
faisant le rapport en reconnaissant dans le dernier facteur la définition du grandissement transverse de l'objet par l'objectif «», on peut réécrire
Évaluation du grandissement transverse de l'objet par l'objectif ainsi que de sa position
[modifier | modifier le wikicode]On peut déterminer le grandissement transverse de par à l'aide de la 2ème relation de conjugaison de Newton [66] «» [117], [134] ou «» soit
La position de se détermine à l'aide de la 1ère relation de conjugaison de Newton [66] «» [116] soit, avec , «» dont on déduit « » ou encore «» et
c.-à-d. « en deçà du foyer principal objet de l'objectif » [136] ou encore
« en » soit «»
c.-à-d. « en deçà du centre optique de l'objectif ».
Retour sur le calcul du grossissement commercial du microscope
[modifier | modifier le wikicode]Reportant la valeur du grandissement transverse de l'objet par l'objectif dans l'expression du « grossissement commercial du microscope » on trouve effectivement un grossissement commercial de grande valeur absolue, en effet
- la distance focale de l'oculaire du microscope est nettement à la distance minimale de vision distincte et
- la valeur absolue du grandissement transverse de l'objet par l'objectif du microscope est grand l'intervalle optique du microscope étant choisi grand devant la distance focale de son objectif,
sa valeur numérique étant soit finalement
Définition du cercle oculaire, établissement de sa position et de sa taille
[modifier | modifier le wikicode]Voir aussi le sous paragraphe « définition du cercle oculaire, établissement de sa position et de sa taille » du paragraphe « lunette de Galilée » [102] plus haut dans ce chapitre, nous rappelons ci-dessous les résultats justifiant la définition du cercle oculaire :
Tous les rayons pénétrant dans le microscope traversent inévitablement sa face d'entrée c.-à-d. l'objectif du microscope, ils en sortiront en passant nécessairement par l'image de l'objectif par le microscope ;
sachant que «» on constate que « l'image de l'objectif par le microscope est aussi l'image de l'objectif par l'oculaire » d'où la définition du « cercle oculaire » ci-dessous et sa conséquence sur la traversée des rayons.
« tous les rayons pénétrant dans le microscope ressortent en traversant le cercle oculaire » et
comme ce dernier est aussi l'endroit de « resserrement maximal autour de l'axe optique principal des rayons émergents » propriété admise, c'est sur le cercle oculaire que l'éclairement est maximal,
c'est donc sur le cercle oculaire qu'il serait préférable de positionner l'œil de l'observateur à condition toutefois que ce soit possible c.-à-d. que le cercle oculaire soit réel et non virtuel [138]
Position du centre du cercle oculaire
[modifier | modifier le wikicode]
Notant « le centre du cercle oculaire », c.-à-d. le conjugué du centre optique de l'objectif par l'oculaire «», on obtient
Notant sa position en utilisant l'une des relations de conjugaison de position de Descartes [25] ou de Newton [66],
Notant par exemple celle de Newton [66] avec «» soit «» et «» déterminée par «» [116]
Notant d'où, après remplacement de par , «» positionnant le centre du cercle oculaire relativement au foyer principal image de l'oculaire soit
le centre du cercle oculaire se trouve légèrement au-delà du foyer principal image de l'oculaire, à au-delà de , il est donc réel « pratiquement confondu avec », plus exactement en soit finalement «» et l'observateur y positionne son œil.
Autre façon de définir le grossissement d'un microscope : Nous avons vu, dans la note « 130 » plus haut dans ce chapitre, une autre façon de définir le grossissement en comparant à angle algébrisé sous lequel l'observateur verrait l'objet en gardant la « même distance objet - œil » mais par observation directe sans passer par le microscope ;
Autre façon de définir le grossissement d'un microscope : dans cette définition la « distance minimale de vision distincte » intervenant pour définir est remplacée, dans la définition de , par « en » soit «» d'où
Autre façon de définir le grossissement d'un microscope : dans cette définition un « grossissement » c.-à-d.
Autre façon de définir le grossissement d'un microscope : dans cette définition un « grossissement de valeur absolue légèrement supérieure à celle du grossissement commercial.
Taille du cercle oculaire pour un objectif de taille précisée
[modifier | modifier le wikicode]Pour déterminer la taille du cercle oculaire il suffit d'évaluer « le grandissement transverse par l'oculaire de l'objet linéique transverse », étant le bord « supérieur » de l'objectif dans le plan d'incidence contenant l'axe optique principal du microscope et au vecteur unitaire voir le schéma de positionnement du cercle oculaire et des rayons extrêmes traversant l'objectif plus bas dans ce chapitre, « étant l'image inversée correspondante par l'oculaire » le grandissement transverse par l'oculaire de l'objet linéique transverse valant,
d'où «» dont on déduit la taille de l'image linéique transverse
ou, en valeur absolue «»
ce qui donne, pour un objectif de de diamètre ou de rayon un cercle oculaire réel de « de rayon »,
Le positionnement de l'œil dans le plan du cercle oculaire est possible dans la mesure où ce dernier est réel et c'est ce qui est fait la taille du cercle oculaire étant de même ordre de grandeur que le diamètre de la pupille de l'œil sous éclairement modéré [118], il n'y a pas de perte de puissance lumineuse moyenne.
Schéma de positionnement du cercle oculaire et des rayons extrêmes traversant l'objectif
[modifier | modifier le wikicode]
Voir ci-contre :
Il existe de nombreux perfectionnements ou utilisations spécifiques d'un microscope optique que l'on peut consulter au paragraphe utilisations et perfectionnement de l'article « Microscope optique » de wikipédia ;
Il y a d'autre part des techniques non optiques de microscopie comme celles décrites dans le paragraphe principaux types de microscopie de l'article « Microscopie » de wikipédia.
Latitude de mise au point du microscope tenant compte de l'accommodation de l'œil de l'observateur
[modifier | modifier le wikicode]En accommodant, un œil normal peut observer nettement un objet situé à une distance comprise entre distance minimale de vision directe avec accommodation maximale et l'infini sans accommodation.
Ayant déterminé la position du pied de l'objet linéique transverse pour qu'un œil normal, n'accommodant pas, puisse observer son image à l'infini à travers le microscope soit « » ou «» c.-à-d. « en deçà du centre optique de l'objectif »,
Ayant déterminé la position Ao, s on se propose d'évaluer de quelle distance et dans quel sens il faut déplacer l'objet pour qu'un œil normal, accommodant au maximum, puisse observer l'image de l'objet à la distance de la position de l'œil ce dernier restant situé au centre du cercle oculaire du microscope, cette variation définissant la latitude de mise au point du microscope ;
pour un œil normal, accommodant au maximum, le pied de l'image de l'objet doit être situé en avant du centre du cercle oculaire lequel est positionné selon « » [139] ou «», d'où la position de relativement au foyer principal image de l'oculaire « » ou relativement au centre optique de l'oculaire « » ;
pour un œil normal, accommodant au maximum, pour déterminer la position du pied de l'objet on utilise les conjugaisons suivantes «» et, à partir de la position de on remonte à celle de par utilisation de la 1ère relation de conjugaison de Newton [66] ou de Descartes [25] appliquée à l'oculaire puis à l'objectif :
- «» avec «» et «» que nous déterminons par application de la 1ère relation de conjugaison de Newton [66] «» [116] soit, en utilisant , « en » soit «» ;
- «» avec « en » «» et « » que nous déterminons par application de la 1ère relation de conjugaison de Newton [66] «» [116] soit, en utilisant , « en » soit «».
Finalement définissant la « latitude de mise au point algébrisée du microscope selon » nous obtenons,
Finalement en reportant les expressions précédemment trouvées, «» puis,
Finalement en factorisant par «», « » soit,
Finalement en tenant compte de «», «» et finalement
il convient donc de rapprocher l'objet de de l'objectif pour que la vision à travers le microscope par un œil n'accommodant pas initialement reste nette lorsque ce dernier accommode au maximum, on dira que la latitude de mise au point du microscope est de.
Notes et références
[modifier | modifier le wikicode]- ↑ Sauf pour un ou deux points particuliers
- ↑ 2,0 2,1 2,2 2,3 2,4 2,5 2,6 et 2,7 Carl Friedrich Gauss (1777 - 1855), mathématicien, astronome et physicien allemand, est considéré comme l'un des plus grands mathématiciens de tous les temps il fut surnommé « le prince des mathématiciens », on lui doit d'importantes contributions dans les trois domaines.
En , à l'âge de dix-neuf ans, Gauss caractérisa presque complètement tous les polygones réguliers constructibles à la règle et au compas et il demanda par la suite qu'un heptadécagone polygone régulier de côtés soit gravé sur son tombeau ; bien d'autres découvertes de mathématiques lui sont dues dont, en particulier, en la 1ère démonstration de la loi de réciprocité quadratique conjecturée par Euler en un nombre premier est congru à un carré de nombre entier modulo un autre nombre premier, par exemple ou ou encore de même que ;
dans le domaine de l'astronomie il publia un travail très important sur le mouvement des corps célestes contenant le développement de la méthode des moindres carrés ; auparavant, en , il développa une nouvelle méthode de calcul lui permettant de prédire où doit se trouver Cérès une planète naine de la ceinture des astéroïdes entre Mars et Jupiter ;
dans le domaine de la physique il est l'auteur de deux des quatre équations de Maxwell gérant l'électromagnétisme ;
certaines de ses contributions n'ont été mises à jour qu'à titre posthume, à la fin du XIXème siècle, Gauss n'ayant publié qu'une partie de ses découvertes.
Leonhard Euler (1707 - 1783) mathématicien et physicien suisse qui passa la plus grande partie de sa vie dans l'Empire russe et en Allemagne ; en mathématiques il fit d'importantes découvertes dans des domaines aussi variés que le calcul infinitésimal et la théorie des graphes, il introduisit également une grande partie de la terminologie et de la notation des mathématiques modernes, en particulier pour l'analyse mathématique, comme la notion de fonction mathématique ; il est aussi connu pour ses travaux en mécanique, en dynamique des fluides, en optique et en astronomie.
James Clerk Maxwell (1831 - 1879) physicien et mathématicien écossais, principalement connu pour ses équations unifiant l'électricité, le magnétisme et l'induction ainsi que pour l'établissement du caractère électromagnétique des ondes lumineuses, mais aussi pour sa distribution des vitesses utilisée dans une description statistique de la théorie cinétique des gaz ; le tire-bouchon fictif permettant de déterminer l'orientation à droite d'un espace tridimensionnel ou le caractère direct d'un triplet de vecteurs a été baptisé « tire-bouchon de Maxwell » en son honneur. - ↑ 3,0 et 3,1 Plus précisément « objets linéiques transverses non proches de la face d'entrée et vus du sommet de celle-ci sous un petit angle » ou « proches de la face d'entrée et vus du centre de courbure de celle-ci sous un petit angle ».
- ↑ Noté simplement en absence d'ambiguïté.
- ↑ Noté simplement en absence d'ambiguïté.
- ↑ Les lentilles sphériques « épaisses » ne sont introduites que pour préciser leur cas particulier, les lentilles sphériques « minces », la définition de ces dernières étant donnée relativement aux 1ères.
- ↑ Il est rappelé que les dioptres sphériques ne sont pas au programme de physique de PCSI mais qu'ils peuvent être introduits pour utiliser des notions au programme comme les lois de Snell–Descartes de la réfraction ou les notions de stigmatisme et aplanétisme approchés.
- ↑ Lequel définit la face d'entrée.
- ↑ 9,0 et 9,1 C.-à-d. l'intersection du dioptre avec l'axe optique principal.
- ↑ Lequel définit la face de sortie.
- ↑ Qui est toujours positive par définition de l'algébrisation.
- ↑ Même si leur algébrisation ne nous sert pas par la suite.
- ↑ Positif si le dioptre d'entrée est convexe c.-à-d. si le centre de courbure est au-delà du sommet dans le sens de la propagation,
négatif si le dioptre d'entrée est concave c.-à-d. si le centre de courbure est en-deçà du sommet dans le sens de la propagation. - ↑ Négatif si le dioptre de sortie est concave c.-à-d. si le centre de courbure est en-deçà du sommet dans le sens de la propagation,
positif si le dioptre de sortie est convexe c.-à-d. si le centre de courbure est au-delà du sommet dans le sens de la propagation. - ↑ 15,0 et 15,1 En fait les faces d'entrée et de sortie ne sont définies qu'à partir du moment où la lentille sphérique est insérée dans un montage, ceci définissant le sens de propagation de la lumière ;
avant insertion le caractère convexe ou concave d'un dioptre sphérique air-verre est défini « de l'air vers le verre », « convexe » si le centre de courbure est du côté du verre et « concave » s'il est du côté de l'air d'où
un dioptre qualifié de « convexe » avant insertion de la lentille dans un montage définit une « face convexe » s'il est à l'« entrée » de la lentille et une « face concave » s'il est à sa « sortie ». - ↑ La lentille boule est simplement une boule.
- ↑ Ou si la face d'entrée est « plane », la face de sortie étant « concave » voir la note « 15 » plus haut dans le chapitre.
- ↑ La lentille demi-boule est simplement une demi-boule.
- ↑ Ou, en inversant la lentille, si la face d'entrée qui était celle de sortie est « concave », la face de sortie étant également « concave » de rayon non algébrisé plus petit que celui de la face d'entrée voir la note « 15 » plus haut dans le chapitre ;
on démontre que cette lentille est convergente dans les conditions de stigmatisme approché de Gauss d'où son nom. - ↑ Ou si la face d'entrée est « plane », la face de sortie étant « convexe » voir la note « 15 » plus haut dans le chapitre.
- ↑ Ou, en inversant la lentille, si la face d'entrée qui était celle de sortie est « convexe », la face de sortie étant également « convexe » de rayon non algébrisé plus petit que celui de la face d'entrée voir la note « 15 » plus haut dans le chapitre ;
on démontre que cette lentille est divergente dans les conditions de stigmatisme approché de Gauss d'où son nom. - ↑ 22,0 et 22,1 Voir le paragraphe « angle limite d'un dioptre » du chap. de la leçon « Signaux physiques (PCSI) ».
- ↑ Les rayons incidents plus éloignés de l'axe que les deux limites d'angle d'incidence en valeur absolue égal à l'angle limite ne sont pas représentés, ils subiraient une réflexion totale sur l'« intérieur » de la face de sortie
- ↑ Willebrord Snell Van Royen ou Snellius (1580 - 1626) humaniste, mathématicien et physicien néerlandais, semble avoir découvert les lois portant son nom avant Descartes sans que ce soit assuré
- ↑ 25,00 25,01 25,02 25,03 25,04 25,05 25,06 25,07 25,08 25,09 25,10 25,11 25,12 25,13 25,14 25,15 25,16 25,17 25,18 25,19 25,20 25,21 25,22 25,23 25,24 25,25 et 25,26 René Descartes (1596 - 1650) mathématicien, physicien et philosophe français, considéré comme l'un des fondateurs de la philosophie moderne, en physique a contribué à l'optique géométrique et en mathématiques est à l'origine de la géométrie analytique.
- ↑ Voir les paragraphes « 1ère loi de Snell-Descartes de la réfraction » et « 2ème loi de Snell-Descartes de la réfraction » du chap. de la leçon « Signaux physiques (PCSI) ».
- ↑ 27,0 et 27,1 Pour le rayon incident arrivant sur le dioptre sphérique verre - air sous l'angle d'incidence limite «», l'émergence étant rasante et par suite « l'inclinaison du rayon réfracté rasant sur l'axe optique principal étant égale à », le point d'intersection de ce rayon réfracté rasant avec l'axe optique principal a pour abscisse, à partir de le centre de courbure du dioptre sphérique, lequel est situé sur la face d'entrée de la lentille demi-boule, «» avec « le projeté orthogonal du point d'incidence sur » d'une part «» et d'autre part l'inclinaison du rayon réfracté sur «» d'où «» ;
pour un rayon incident très proche de l'axe optique principal arrivant sur le dioptre sphérique verre - air sous un angle d'incidence de valeur absolue très petite étant considéré comme un infiniment petit d'ordre un, l'émergence se fait sous l'angle de réfraction déterminé par les lois de Snell-Descartes de la réfraction référence note « 26 » plus haut dans ce chapitre soit, en utilisant la 2ème loi «» dont le développement limité D.L. à l'ordre un est «» «» voir le paragraphe « D.L. à l'ordre un de quelques fonctions usuelles » du chap. de la leçon « Outils mathématiques pour la physique (PCSI) » l'angle de réfraction «» est aussi un infiniment petit d'ordre un de valeur absolue légèrement plus grande dont la conséquence est que « le rayon réfracté se dirige vers l'axe optique principal incliné par rapport à ce dernier d'un angle » également un infiniment petit d'ordre un ; le point d'intersection de ce rayon réfracté avec l'axe optique principal a pour abscisse, à partir de , «» avec « le projeté orthogonal du point d'incidence sur » d'une part «» voir le paragraphe « D.L. à l'ordre un de quelques fonctions usuelles » du chap. de la leçon « Outils mathématiques pour la physique (PCSI) » et d'autre part l'inclinaison du rayon réfracté sur « » d'où «» ;
les rayons émergents correspondant aux rayons incidents choisis ci-dessus provenant du même point objet ne recoupant pas l'axe au même endroit, la lentille demi-boule n'est donc pas stigmatique rigoureuse pour le point . - ↑ Utiliser un diaphragme suffisamment étroit ayant pour axe l'axe optique principal de la lentille demi-boule, revient à ne considérer que les rayons incidents très proches de ; ces derniers arrivant sur le dioptre sphérique verre - air sous un angle d'incidence de valeur absolue très petite considéré comme un infiniment petit d'ordre un, l'émergence se fait alors sous un angle de réfraction déterminé par les lois de Snell-Descartes de la réfraction référence note « 26 » plus haut dans ce chapitre soit, en utilisant la 2ème loi «» dont le D.L. à l'ordre un est « » voir le paragraphe « D.L. à l'ordre un de quelques fonctions usuelles » du chap. de la leçon « Outils mathématiques pour la physique (PCSI) » l'angle de réfraction «» est aussi un infiniment petit d'ordre un de valeur absolue légèrement plus grande dont la conséquence est que « les rayons réfractés sélectionnés se dirigent vers l'axe optique principal inclinés par rapport à ce dernier d'un angle » également un infiniment petit d'ordre un ; l'intersection de et des rayons réfractés sélectionnés ayant été déterminée dans la note « 27 » plus haut dans ce chapitre « à l'ordre un en » et cette abscisse étant indépendante de nous en déduisons qu'il y convergence de tous les rayons réfractés en un point fixe noté «», cette convergence assurant le stigmatisme approché de la lentille demi-boule pour .
- ↑ Plus précisément si «, et » ;
comme «», la condition «» peut être remplacée par « non petit ». - ↑ Sauf pour un point qui sera précisé ultérieurement où le stigmatisme est rigoureux.
- ↑ Nous voyons, dans le paragraphe «conséquence sur les axes optiques secondaires d'une lentille mince» plus bas dans ce chapitre, que l'émergent est dans le prolongement de l'incident correspondant, ce qui fait que l'« axe optique secondaire associé un incident est une droite, usuellement notée ».
- ↑ En effet le rayon incident sur le dioptre d'entrée ainsi que le rayon réfracté servant de rayon incident sur le dioptre de sortie doivent rester proches du sommet de chaque dioptre donc du point commun les modélisant.
- ↑ En effet si l'objet est accolé à la face d'entrée, il ne peut être « considéré comme linéique » que si on peut négliger la courbure de la face d'entrée et ceci nécessite que l'arc de cercle puisse être confondu avec un segment c.-à-d. qu'il soit petit ;
ceci est effectivement en accord avec les conditions générales qui sont que l'angle sous lequel l'objet accolé à la face d'entrée respectivement de sortie est vu du centre de courbure du dioptre d'entrée respectivement de sortie sous un petit angle car les centres de courbure du dioptre d'entrée et de sortie sont éloignés du centre optique. - ↑ En effet la lumière passant d'un milieu moins réfringent à un milieu plus réfringent, l'angle d'émergence est plus petit que l'angle d'incidence.
- ↑ En effet la lumière passant d'un milieu plus réfringent à un milieu moins réfringent, l'angle d'émergence est plus grand que l'angle d'incidence.
- ↑ Il s'agit de stigmatisme approché et non rigoureux comme nous l'avons vu dans le dernier schéma du paragraphe « exemple de systèmes dioptriques centrés, les lentilles sphériques » plus haut dans ce chapitre.
- ↑ Il s'agit de stigmatisme approché et non rigoureux comme le justifie la loi du retour inverse appliqué au résultat précédent.
- ↑ Les points et n'appartenant pas au même espace optique le 1er étant dans l'espace objet et le 2ème dans l'espace image ce ne sont que leurs positions géométriques qui peuvent être qualifiées de symétriques relativement à .
- ↑ Voir les 1er, 2èmes et 3èmes schémas à partir de la gauche du paragraphe « exemple de systèmes dioptriques centrés : les lentilles sphériques » plus haut dans ce chapitre.
- ↑ Voir les 4ème, 5èmes et 6èmes schémas à partir de la gauche du paragraphe « exemple de systèmes dioptriques centrés : les lentilles sphériques » plus haut dans ce chapitre.
- ↑ Ou encore ou simplement en absence d'ambiguïté.
- ↑ 42,0 et 42,1 C.N. pour qu'il y ait stigmatisme approché de la lentille pour les points de cet axe, la 2ème condition de paraxialité étant évidemment réalisée puisque l'axe optique secondaire passe par le centre optique.
- ↑ 43,0 et 43,1 Dans les conditions de Gauss de stigmatisme approché bien sûr.
- ↑ Ou encore ou simplement en absence d'ambiguïté.
- ↑ 45,0 et 45,1 Nous verrons, plus bas dans ce chapitre, que le « repérage de Descartes des points objet et image » sur l'axe optique principal se fait à partir du centre optique choisi comme origine, ceci étant en accord avec le repérage de Descartes du point relativement à chaque dioptre sphérique à condition que l'origine de ces repérages soit le sommet de chaque dioptre, sommets qui se confondent avec le centre optique dans la limite de lentille sphérique mince.
- ↑ C'est aussi l'abscisse de Descartes du foyer principal objet de la lentille mince.
- ↑ Quand on parle de « distance focale » sans préciser c'est « toujours la distance focale image » ; c'est donc elle qui joue le rôle le plus important.
- ↑ C'est aussi l'abscisse de Descartes du foyer principal image de la lentille mince.
- ↑ La justification de la définition de la vergence d'une lentille mince est faite dans le paragraphe « 1ère relation de conjugaison (ou relation de conjugaison de position) de Descartes » plus bas dans ce chapitre.
- ↑ 50,0 et 50,1 On peut vérifier à l'aide du 3ème rayon l'exactitude de la construction, mais ce n'est pas indispensable.
- ↑ Positionnement de l'objet lors de son observation à travers une loupe, l'objet réel doit donc être placé entre la face d'entrée et le plan focal objet de la loupe, ceci permettant d'obtenir une image virtuelle droite et agrandie.
- ↑ 52,0 et 52,1 Le point à l'infini de l'axe optique principal est le point commun « de fermeture » de l'axe sur lui-même une droite étant la limite d'un cercle dont le rayon tend vers l'infini, il est donc à la fois « réel » et « virtuel » mais dans la pratique le point objet est à une distance finie très grande que l'on considère comme infinie, il est donc réel.
- ↑ L'image étant à l'infini elle n'est a priori ni réelle ni virtuelle mais si la lentille convergente est utilisée comme projecteur c.-à-d. dont le but est de donner une image réelle agrandie), l'objet est positionné à une distance très légèrement plus grande que la distance focale ce qui entraîne une image « réelle » très éloignée considérée comme à l'infini.
- ↑ L'image étant à l'infini elle n'est a priori ni réelle ni virtuelle mais si la lentille divergente est utilisée pour agrandir un objet virtuel, l'objet est positionné à une distance très légèrement plus petite que la distance focale ce qui entraîne une image « réelle » très éloignée considérée comme à l'infini.
- ↑ Si l'objet ponctuel était à l'infini sur , son image serait le foyer principal image et ne serait donc pas à déterminer.
- ↑ C.-à-d. que le rayon incident passe par le point à l'infini de cet axe .
- ↑ 57,0 57,1 57,2 et 57,3 La méthode de construction est la même quelle que soit la nature de la lentille mince, convergente ou divergente.
- ↑ Si l'image ponctuelle était à l'infini sur , son objet conjugué serait le foyer principal objet et ne serait donc pas à déterminer.
- ↑ C.-à-d. que le rayon émergent passe par le point à l'infini de cet axe .
- ↑ Orientation de l'espace définie par le mouvement de rotation et translation associées d'un tire-bouchon de Maxwell voir l'« introduction du paragraphe produit vectoriel de deux vecteur » du chap. de la leçon « Outils mathématiques pour la physique (PCSI) » ;
James Clerk Maxwell (1831 - 1879) physicien et mathématicien écossais, principalement connu pour ses équations unifiant l'électricité, le magnétisme et l'induction ainsi que pour l'établissement du caractère électromagnétique des ondes lumineuses, mais aussi pour sa distribution des vitesses utilisée dans une description statistique de la théorie cinétique des gaz ; le tire-bouchon fictif portant son nom a été baptisé ainsi en son honneur. - ↑ Voir le paragraphe « base directe d'un espace orienté à droite » du chap. de la leçon « Outils mathématiques pour la physique (PCSI) ».
- ↑ Levant le pouce de la main droite dans le sens du 1er vecteur, l'index pointant dans le sens du 2ème vecteur, « le sens du 3ème vecteur est donné par le majeur courbé vers la paume de la main droite » ceux qui se souviennent de leur enfance pourraient encore appeler cette règle « la règle de l'apprenti cow-boy droitier » ; il existe d'autres règles équivalentes :
« règle de l'auto-stoppeur (droitier) » : l'avant bras droit étant dans le sens du 1er vecteur, la poigne de la main droite courbée dans le sens du 2ème vecteur, le pouce est alors levé dans le sens du 3ème vecteur,
« règle du tire-bouchon de Maxwell » : le tire-bouchon tournant du 1er vecteur vers du 2ème, il s'enfonce dans le bouchon fixe dans le sens de du 3ème vecteur,
« règle du bonhomme d'Ampère » : le bonhomme d'Ampère se couchant sur la direction du 1er vecteur, ce vecteur lui entrant par les pieds et lui sortant par la tête, regardant droit devant dans le sens du 2ème vecteur, il tend le bras gauche perpendiculairement à son corps dans le sens du 3ème vecteur,
et bien d'autres règles que vous pouvez vous-même inventer.
James Clerk Maxwell (1831 - 1879) physicien et mathématicien écossais, principalement connu pour ses équations unifiant l'électricité, le magnétisme et l'induction ainsi que pour l'établissement du caractère électromagnétique des ondes lumineuses, mais aussi pour sa distribution des vitesses utilisée dans une description statistique de la théorie cinétique des gaz ; le tire-bouchon fictif permettant de déterminer le caractère direct d'un triplet de vecteurs a été baptisé « tire-bouchon de Maxwell » en son honneur.
André-Marie Ampère (1775 - 1836), mathématicien, physicien, chimiste et philosophe français, peut être considéré comme l'un des premiers artisans de la mathématisation de la physique, il a édifié les fondements théoriques de l'électromagnétisme et a découvert les bases de l'électronique de la matière ; c'est lui qui inventa le bonhomme fictif portant son nom et permettant de déterminer le caractère direct d'un triplet de vecteurs. - ↑ Ici, s'agissant d'un système dioptrique, les sens incident et émergent de l'axe optique principal sont les mêmes.
- ↑ En effet «» correspond à situé avant la face d'entrée de la lentille donc dans l'espace objet réel et
En effet «» correspond à situé après la face d'entrée de la lentille donc dans l'espace objet virtuel. - ↑ En effet «» correspond à situé après la face de sortie de la lentille donc dans l'espace image réelle et
En effet «» correspond à situé avant la face de sortie de la lentille donc dans l'espace image virtuelle. - ↑ 66,00 66,01 66,02 66,03 66,04 66,05 66,06 66,07 66,08 66,09 66,10 66,11 66,12 66,13 66,14 66,15 66,16 66,17 66,18 66,19 66,20 66,21 66,22 66,23 66,24 66,25 66,26 66,27 66,28 66,29 66,30 66,31 66,32 66,33 66,34 et 66,35 Isaac Newton (1643 - 1727) philosophe, mathématicien, physicien, astronome, alchimiste et théologien anglais, connu essentiellement de nos jours pour avoir fondé la mécanique classique, pour sa théorie de la gravitation et aussi pour la création du calcul infinitésimal ; en optique il a développé une théorie de la couleur et a aussi inventé un télescope composé d'un miroir primaire concave et d'un miroir secondaire plan, télescope connu de nos jours sous le nom de télescope de Newton.
- ↑ En effet «» correspond à situé avant le plan focal objet de la lentille pour une lentille convergente, le point objet est réel avec ,
En effet « σo < 0 » correspond à Ao situé avant le plan focal objet de la lentille ( pour une lentille divergente, le point objet est réel quelle que soit la distance ou
En effet « σo < 0 » correspond à Ao situé avant le plan focal objet de la lentille (pour une lentille divergente, le point objet est virtuel avec et
En effet «» correspond à situé après le plan focal objet de la lentille pour une lentille convergente, le point objet est réel avec ou
En effet « σo > 0 » correspond à Ao situé après le plan focal objet de la lentille (pour une lentille convergente, le point objet est virtuel quelle que soit la distance ,
En effet « σo > 0 » correspond à Ao situé après le plan focal objet de la lentille ( pour une lentille divergente, le point objet est virtuel avec . - ↑ En effet «» correspond à situé après le plan focal image de la lentille pour une lentille convergente, le point image est réel avec ,
En effet « σi > 0 » correspond à Ai situé après le plan focal image de la lentille ( pour une lentille divergente, le point image est réel quelle que soit la distance ou
En effet « σi > 0 » correspond à Ai situé après le plan focal image de la lentille (pour une lentille divergente, le point image est virtuel avec et
En effet «» correspond à situé avant le plan focal image de la lentille pour une lentille convergente, le point image est virtuel quelle que soit la distance ou
En effet « σi < 0 » correspond à Ai situé avant le plan focal image de la lentille (pour une lentille convergente, le point image est réel avec ,
En effet « σi < 0 » correspond à Ai situé avant le plan focal image de la lentille ( pour une lentille divergente, le point image est virtuel avec . - ↑ La restriction n'est pas gênante car la position de l'image de est connue, étant un point double.
- ↑ Voir le paragraphe « définition du grandissement transverse d'un objet linéique transverse dans le cas d'un système optique unidirectionnel aplanétique » du chap. de la leçon « Signaux physiques (PCSI) ».
- ↑ Dans la mesure où l'objet obéit aux conditions de Gauss d'aplanétisme approché de la lentille, l'image est effectivement linéique transverse.
- ↑ La restriction n'est pas gênante car tous les points de la lentille mince étant des points d'incidence sur cette dernière sont leur propre image et par suite le grandissement transverse d'un objet accolé à la lentille vaut .
- ↑ L'image sera droite pour un objet réel donnant une image virtuelle ou
L'image sera droite pour un objet virtuel donnant une image réelle . - ↑ L'image sera inversée pour un objet réel donnant une image réelle non réalisable avec une lentille divergente correspondant à car, pour un objet réel, l'image est virtuelle ou
L'image sera inversée pour un objet virtuel donnant une image virtuelle non réalisable avec une lentille convergente correspondant à car, pour un objet virtuel, l'image est réelle. - ↑ La restriction n'est pas gênante car la position de l'image de et celle de l'image de est connue, ce sont respectivement et .
- ↑ Qui peut encore s'écrire «» montrant que les abscisses image et objet de Newton sont nécessairement de signe contraire soit :
si est en deçà du foyer objet correspondant à , est au-delà du foyer image correspondant à et
si est au-delà du foyer objet correspondant à , est en deçà du foyer image correspondant à . - ↑ Nous n'avons vérifié la propriété « point double » que du point de vue de la « conjugaison approchée » mais nous savons que cette propriété est encore valable du point de vue de la conjugaison rigoureuse la lentille mince étant stigmatique rigoureux pour son centre optique.
- ↑ La restriction n'est pas gênante car si , et ,
La restriction n'est pas gênante car si , et .
Moyen mnémotechnique pour retenir la formule : retenir le signe et que la valeur absolue du grandissement faire intervenir un rapport de grandeurs objets mais s'agit-il de ou ?
Moyen mnémotechnique pour retenir la formule : Pour cela se souvenir que le grandissement sera nul si l'objet est à l'infini d'où doit être au dénominateur et par suite . - ↑ La restriction n'est pas gênante car si , , et ,
La restriction n'est pas gênante car si , , et .
Moyen mnémotechnique pour retenir la formule : retenir le signe et que la valeur absolue du grandissement faire intervenir un rapport de grandeurs images mais s'agit-il de ou ?
Moyen mnémotechnique pour retenir la formule : Pour cela se souvenir que le grandissement sera infini si l'image est à l'infini d'où doit être au numérateur et par suite . - ↑ L'image sera inversée pour une lentille convergente respectivement si l'objet est en deçà du foyer principal objet respectivement si l'image est au-delà du foyer principal image correspondant nécessairement à un objet réel respectivement une image réelle et
L'image sera inversée pour une lentille divergente respectivement si l'objet est au-delà du foyer principal objet respectivement si l'image est en deçà du foyer principal image correspondant nécessairement à un objet virtuel respectivement une image virtuelle. - ↑ L'image sera droite pour une lentille convergente respectivement si l'objet est au-delà du foyer principal objet respectivement si l'image est en deçà du foyer principal image correspondant à un objet réel entre le plan focal objet et la lentille ou un objet virtuel respectivement une image réelle entre le plan focal image et la lentille ou une image virtuelle et
L'image sera droite pour une lentille divergente respectivement si l'objet est en deçà du foyer principal objet respectivement si l'image est au-delà du foyer principal image correspondant à un objet virtuel entre le plan focal objet et la lentille ou un objet réel respectivement une image virtuelle entre le plan focal image et la lentille ou une image réelle. - ↑ étant comme d'habitude le pied de l'objet sur l'axe optique principal de la lentille mince.
- ↑ Nous choisissons de démontrer les relations de conjugaison de Descartes et de Newton pour une lentille mince convergente, nous admettrons que ces relations restent inchangées pour une lentille mince divergente mais la démonstration pourrait y être faite de la même façon.
- ↑ Pour cela il faut que soit en deçà du foyer principal objet de la lentille mince convergente ce choix est fait pour que la figure soit étendue donc la plus claire possible, nous admettrons qu'un autre choix, quel qu'il soit, conduise aux mêmes relations de conjugaison de Descartes et de Newton ;
pour démontrer les relations de conjugaison de Descartes et de Newton pour une lentille mince divergente et pour que la figure soit étendue on pourrait choisir un objet linéique transverse virtuel de pied au-delà du foyer principal objet , l'image, alors virtuelle, conduirait à une extension de la figure de part et d'autre de la lentille. - ↑ Ces dernières étant valables pour une lentille mince convergente ou divergente quelles soient la nature et la position de l'objet, il en est donc de même des relations de conjugaison de position que l'on établit dans ce paragraphe.
- ↑ Quand on a l'égalité entre deux fractions les grandeurs sont appelées « extrêmes » et « moyens », l'égalité des deux fractions étant équivalente à «» c.-à-d. à l'égalité du produit des extrêmes et celui des moyens on parle encore de l'égalité des produits en croix.
- ↑ Seul le rayon moyen du pinceau a été représenté sur le schéma pour rendre ce dernier le plus clair possible ; il en a été de même pour le pinceau émergent de la lentille.
- ↑ Pour que l'image de soit la même quelle que soit la direction moyenne du pinceau issu de , il faut que « la condition de paraxialité du rayon moyen de ce pinceau soit réalisée c.-à-d. » et aussi que « reste proche de ».
- ↑ 89,0 et 89,1 On admet que « la condition de paraxialité du rayon moyen de ce pinceau issu de » ainsi que « la proximité entre le point d'incidence et le centre optique de la lentille » entraîne « la paraxialité du pinceau émergent convergeant en , d'où ».
- ↑ On écrit l'égalité car, dans les conditions de Gauss, on ne considère que les termes prépondérants d'ordre un mais en fait ce n'est qu'une approximation à l'ordre un d'où, dans la démonstration, «».
- ↑ 91,0 et 91,1 Joseph Louis Lagrange (1736 - 1813) mathématicien, mécanicien et astronome italien, naturalisé français vers la fin du XVIIIème siècle de nom italien Giuseppe Luigi Lagrangia ;
on lui doit, entre autres, d'avoir jeté en mathématiques les bases du calcul variationnel, calcul qu'il appliqua en mécanique pour résoudre quelques problèmes propagation du son, corde vibrante, librations de la Lune c.-à-d. petites variations de son orbite ;
en , alors installé à Paris, il publia son livre de mécanique analytique dont le formalisme a permis, un siècle et demi plus tard, l'ébauche de la mécanique quantique, il est aussi l'un des pères du système métrique et de la division décimale des unités ;
on remarquera que le domaine de l'optique n'est pas pour Lagrange un domaine privilégié ni pour Helmholtz non plus ! - ↑ 92,0 et 92,1 Hermann Ludwig Ferdinand von Helmholtz (1821 - 1894) physiologiste et physicien allemand, à qui on doit d'importantes contributions dans la perception des sons et des couleurs ainsi que surtout dans le domaine de la thermodynamique ;
on remarquera que le domaine de l'optique n'est pas pour Helmholtz un domaine privilégié ni pour Lagrange non plus ! - ↑ La relation de Lagrange - Helmholtz d'une lentille mince est généralisable à tout système dioptrique pour lequel les espaces d'entrée et de sortie sont de même indice, plus précisément on démontre que la relation de Lagrange - Helmholtz s'écrit « pour un système dioptrique quelconque » ce qui donne effectivement « quand » ;
nous avons vu la relation de Lagrange - Helmholtz pour un miroir plan relation généralisable à tout système catadioptrique unidirectionnel «», le signe du produit « grandissement angulaire - grandissement transverse » caractérisant la nature dioptrique ou catadioptrique du système. - ↑ Le rétroéclairage est une technique d'éclairage par l'arrière, exemple d'objet rétroéclairé « diapositive éclairée par source située derrière ».
- ↑ L'image par une lentille divergente est réelle si l'objet est virtuel entre la face de sortie de la lentille et son plan focal objet, alors qu'une lentille convergente donne une image réelle pour un objet réel situé en deçà du plan focal objet pour mémoire l'image d'un objet virtuel par une lentille convergente est aussi réelle.
- ↑ Cette condition nécessaire n'est toutefois pas suffisante.
- ↑ Voir le paragraphe « 1ère relation de conjugaison (ou relation de conjugaison de position) de Descartes » plus haut dans ce chapitre.
- ↑ 98,0 98,1 98,2 98,3 98,4 98,5 et 98,6 Friedrich Wilhelm Bessel (1784 - 1846) astronome, mathématicien, géodésien et physicien allemand, connu pour avoir défini les fonctions de Bessel et aussi avoir effectué en les 1ères mesures précises de la distance d'une étoile fixe l'« étoile binaire et circumpolaire 61 Cygni » système binaire d'étoiles naines oranges quasi identiques situées dans la constellation du Cygne.
- ↑ 99,0 et 99,1 Jean Thiébault Silbermann (1806 - 1865) physicien français à qui on doit les 1ères mesures de thermochimie et quelques inventions en optique dont un focomètre.
- ↑ En effet la dérivée partielle de la valeur absolue du grandissement transverse «» relativement à à fixée se calcule selon « » soit «» après simplification.
- ↑ En effet la dérivée partielle de la valeur absolue du grandissement transverse «» relativement à à fixée se calcule selon « » soit «» après simplification.
- ↑ 102,0 102,1 102,2 102,3 et 102,4 Galileo Galilei (1564 - 1642) mathématicien, géomètre, physicien et astronome italien plus exactement pour l'époque « florentin », l'unification de l'Italie ne datant que de , à qui on doit en l'amélioration de la longue vue inventée par l'opticien hollandais Hans Lippershey (1570 - 1619) en lunette d'observation des objets célestes sans inversion de l'image par ajout d'une lentille divergente ; dès en observant les phases de Vénus, il est convaincu que le géocentrisme ne permet pas une explication simple de cette observation contrairement à l'héliocentrisme théorie physique dont l'essor est essentiellement dû à Nicolas Copernic (1473 - 1543) chanoine, médecin et astronome polonais et défend cette thèse en poursuivant ses observations jusqu'en où il fût déclaré suspect d'hérésie par l'Inquisition romaine et dût adjurer ; il a aussi posé les bases de la mécanique en étudiant l'équilibre et le mouvement des corps solides en particulier leur chute, leur translation rectiligne et leur inertie ainsi que la généralisation des mesures de temps en particulier par l'étude de l'isochronisme du pendule.
- ↑ 103,0 et 103,1 Le foyer principal image de l'objectif étant le foyer principal objet de l'oculaire.
- ↑ 104,0 104,1 et 104,2 En effet est géométriquement symétrique relativement à .
- ↑ Une 1ère influence d'un oculaire divergent est une diminution de l'encombrement de la lunette.
- ↑ 106,0 et 106,1 étant l'axe optique secondaire de l'oculaire associé au foyer secondaire objet de ce dernier c.-à-d. le foyer secondaire image associé à l'axe secondaire de l'objectif.
- ↑ 107,0 et 107,1 Nombre sans unité, et devant être exprimés dans la même unité.
- ↑ 108,0 et 108,1 Les angles étant algébrisés, la positivité du grossissement définit une image droite respectivement la négativité une image inversée à l'infini d'un objet à l'infini.
- ↑ 109,0 109,1 et 109,2 Sous conditions de Gauss les angles sont petits et on peut confondre la tangente d'un angle avec la valeur de l'angle en à l'ordre un en cet angle.
- ↑ 110,0 et 110,1 Les signes sont satisfaisants car , et .
- ↑ Les signes sont satisfaisants car , et .
- ↑ 112,0 et 112,1 On écrit l'égalité car, dans les conditions de Gauss, on ne considère que les termes prépondérants d'ordre un mais en fait ce n'est qu'une approximation à l'ordre un d'où, dans la démonstration, «».
- ↑ Une seconde influence d'un oculaire divergent est l'obtention d'une image droite due au fait que le grossissement est positif de même signe que .
- ↑ 114,0 114,1 114,2 et 114,3 Dans l'hypothèse où le cercle oculaire serait virtuel, l'œil de l'observateur ne pourrait évidemment pas y être positionné, il conviendrait alors de placer ce dernier dans l'espace image réelle le plus près possible du cercle oculaire c.-à-d. sur la face de sortie de la lunette laquelle est l'oculaire lui-même.
- ↑ 115,0 et 115,1 On rappelle que le foyer principal objet de l'oculaire est confondu avec le foyer principal image de l'objectif pour que la lunette soit afocale.
- ↑ 116,0 116,1 116,2 116,3 116,4 et 116,5 Voir le paragraphe « 1ère relation de conjugaison (ou relation de conjugaison de position) de Newton» plus haut dans ce chapitre.
- ↑ 117,0 117,1 117,2 et 117,3 Voir le paragraphe « 2ème relation de conjugaison (ou relation de conjugaison de grandissement transverse) de Newton » plus haut dans ce chapitre.
- ↑ 118,0 118,1 et 118,2 Le diamètre de la pupille de l'œil varie entre et , à fort éclairement et dans l'obscurité.
- ↑ Pour la même vergence de l'objectif et une vergence opposée de l'oculaire, la lunette astronomique est plus encombrante plus longue que la lunette de Galilée.
- ↑ 120,0 et 120,1 Ceci n'est pas à considérer comme un défaut majeur car le but d'une lunette astronomique est d'observer les objets d'une voûte céleste en rotation, le haut devenant le bas après quelques heures.
- ↑ 121,0 et 121,1 Les signes sont satisfaisants car , et .
- ↑ Un second léger inconvénient d'un oculaire convergent est l'obtention d'une image inversée dû au fait que le grossissement est négatif.
- ↑ Il est difficile de dire qui a inventé le 1er microscope optique :
les 1ers à s'en être prévalu sont l'opticien hollandais Hans Janssen et son fils Zacharias Janssen (v.1588 - v.1631) devenu à l'âge adulte, lunetier et fabricant de lentilles mais la date que ce dernier mentionne étant est pour le moins improbable en ce qui le concerne ou en ce qui concerne la date ;
le 2nd à être cité est Galileo Galilei (1564 - 1642) mathématicien, géomètre, physicien et astronome italien plus exactement pour l'époque « florentin », l'unification de l'Italie ne datant que de , qui a développé un microscope composé d'une lentille convexe et d'une autre concave en . - ↑ 124,0 et 124,1 L'antécédent par l'oculaire du point image à l'infini de étant son foyer principal objet .
- ↑ L'intervalle optique est usuellement noté mais dans ce cours représente l'axe optique principal !
- ↑ Sera justifié dans les paragraphes « évaluation du grandissement transverse de l'objet par l'objectif ainsi que de sa position » et « retour sur le calcul du grossissement commercial du microscope » plus bas dans ce chapitre.
- ↑ étant l'axe optique secondaire de l'oculaire associé au foyer secondaire objet de ce dernier lequel se détermine comme intersection du rayon émergent de l'objectif et du plan focal objet de l'oculaire.
- ↑ L'antécédent par l'oculaire du point image à l'infini de l'axe optique secondaire étant le foyer secondaire objet associé à .
- ↑ En fait cette manière de définir le grossissement donne une valeur toujours inférieure aux autres façons de le définir.
- ↑ Une autre façon de définir le grossissement est de comparer à l'angle algébrisé sous lequel l'observateur verrait l'objet en gardant la « même distance objet - œil » mais par observation directe sans passer par le microscope.
- ↑ Distance encore appelée « distance minimale de vision distincte ».
- ↑ Les signes sont satisfaisants car et d'où le signe .
- ↑ On a utilisé .
- ↑ Bien sûr on pourrait utiliser la 2ème relation de conjugaison de Descartes voir le paragraphe « 2ème relation de conjugaison (ou relation de conjugaison de grandissement transverse) de Descartes » plus haut dans ce chapitre mais à condition d'utiliser simultanément la 1ère car si est connue, ne l'est pas avant d'avoir utilisé la relation de conjugaison de position de Descartes voir le paragraphe « 1ère relation de conjugaison (ou relation de conjugaison de position) de Descartes » plus haut dans ce chapitre ; l'avantage de la relation de conjugaison de grandissement transverse de Newton c'est qu'elle nécessite de connaître l'abscisse image ou objet mais qu'il n'est pas nécessaire de connaître les deux.
- ↑ On vérifie qu'il faut choisir l'intervalle optique grand devant la distance focale de l'objectif pour obtenir un grandissement transverse de l'objet par l'objectif grand en valeur absolue.
- ↑ L'objet est donc quasiment dans le plan focal objet de l'objectif.
- ↑ Nous avons vu dans la note « 130 » plus haut dans ce chapitre qu'une autre façon possible de définir le grossissement est de comparer à l'angle algébrisé sous lequel l'observateur verrait l'objet en gardant la « même distance objet - œil » mais par observation directe sans passer par le microscope, nous ferons le calcul de ce grossissement dans le paragraphe « position du centre du cercle oculaire (autre façon de définir le grossissement d'un microscope) » plus bas dans ce chapitre.
- ↑ Dans l'hypothèse où le cercle oculaire serait virtuel, l'œil de l'observateur ne pourrait évidemment pas y être positionné, il conviendrait alors de placer ce dernier dans l'espace image réelle le plus près possible du cercle oculaire c.-à-d. sur la face de sortie du microscope laquelle est l'oculaire lui-même.
- ↑ Voir le paragraphe « position du centre du cercle oculaire (d'un microscope) » plus haut dans ce chapitre.





![{\displaystyle {\big ]}\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f6409e9848c1422eef16462fbeae301d8fa0f831)

![{\displaystyle {\big ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/31d63350d68291e3f56604a089e0e0b5a86c2472)




















































![{\displaystyle \;O\;\in \,\left[IJ\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4230388e76266fae8b0771caf9a8f77e71abc36)
![{\displaystyle \;J{\big ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/957321680952b79e72a5e7ef34ce3858b1e9a5f1)









![{\displaystyle \;{\big [}O\;{\stackrel {\mathcal {L}}{\longrightarrow }}\;O{\big ]}\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/713e1a4477ff55551c8394fd5b2c21306dafe882)
































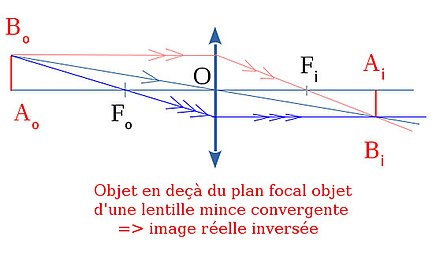
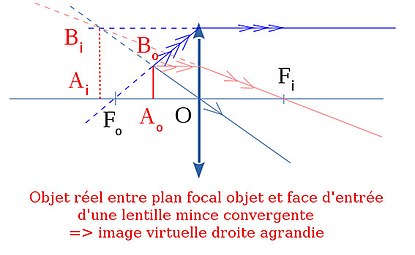
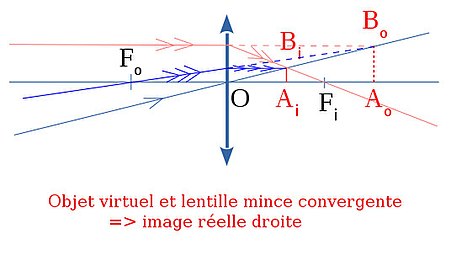








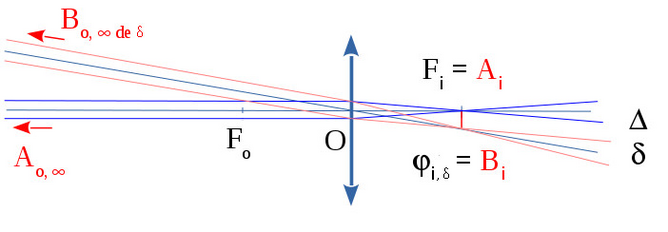





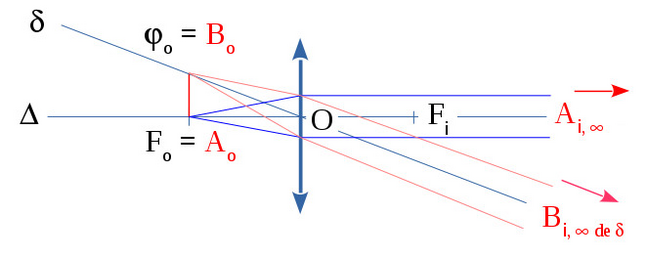








![Construction de l'image par une lentille mince convergente [57] d'un objet ponctuel réel par utilisation de la notion de foyer secondaire objet](http://upload.wikimedia.org/wikipedia/commons/thumb/d/d3/Lentille_mince_convergente_-_foyer_secondaire_objet.jpg/653px-Lentille_mince_convergente_-_foyer_secondaire_objet.jpg)
![Construction de l'image par une lentille mince convergente [57] d'un objet ponctuel réel par utilisation de la notion de foyer secondaire image](http://upload.wikimedia.org/wikipedia/commons/thumb/6/6f/Lentille_mince_convergente_-_foyer_secondaire_image.jpg/634px-Lentille_mince_convergente_-_foyer_secondaire_image.jpg)



![Construction de l'objet conjugué par une lentille mince divergente [57] d'une image ponctuelle réelle par utilisation de la notion de foyer secondaire image](http://upload.wikimedia.org/wikipedia/commons/thumb/2/2a/Lentille_mince_divergente_-_foyer_secondaire_image.jpg/655px-Lentille_mince_divergente_-_foyer_secondaire_image.jpg)
![Construction de l'objet conjugué par une lentille mince divergente [57] d'une image ponctuelle réelle par utilisation de la notion de foyer secondaire objet](http://upload.wikimedia.org/wikipedia/commons/thumb/a/a8/Lentille_mince_divergente_-_foyer_secondaire_objet.jpg/629px-Lentille_mince_divergente_-_foyer_secondaire_objet.jpg)
































![{\displaystyle \;(\sigma _{i}\,,\,f_{i}){\big ]}\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/88b85241894d64c490a24de632a2c93119f7d0f2)







































































































































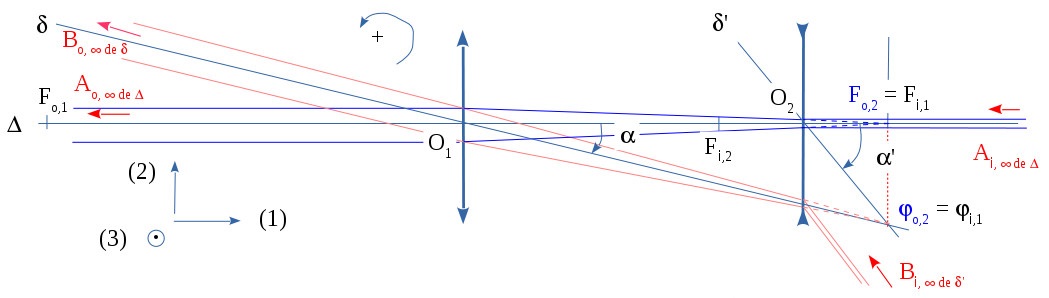



![{\displaystyle \;A_{o,\,\infty }B_{o,\,\infty \,{\text{de}}\,\delta }{\big ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3a40b77639d54aeaabd95b1987b4f325d855e5b4)








































































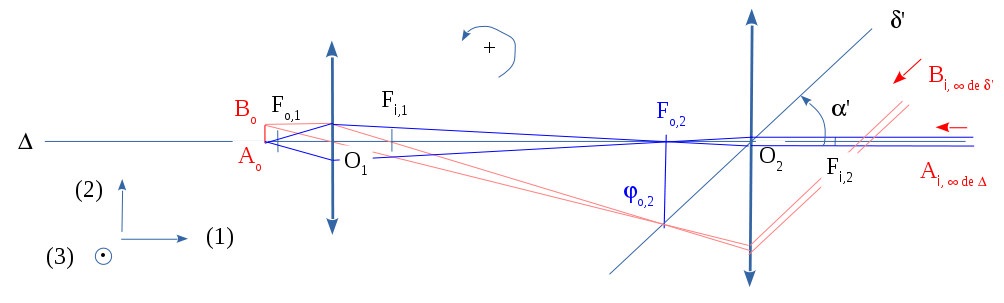




































































































![{\displaystyle \;\sigma _{o,\,1}(A_{o,\,a})={\overline {F_{o,\,1}A_{o,\,a}}}=-{\dfrac {f_{i,\,1}^{2}\left[d\,(f_{i,\,1}+e)-f_{i,\,2}^{2}\right]}{e\,d\,(f_{i,\,1}+e)+f_{i,\,2}^{2}\,f_{i,\,1}}}\simeq -0,01\;cm\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6ccf56f1c6685def2bba28d8b347ad33bfac750b)

![{\displaystyle \;{\overline {A_{o,\,s}A_{o,\,a}}}=-{\dfrac {f_{i,\,1}^{2}\left[d\,(f_{i,\,1}+e)-f_{i,\,2}^{2}\right]}{e\,d\,(f_{i,\,1}+e)+f_{i,\,2}^{2}\,f_{i,\,1}}}+{\dfrac {f_{i,\,1}^{2}}{e}}\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aed2e7fc6756a11a57f18beb29dcd05d71679896)


![{\displaystyle ={\dfrac {f_{i,\,1}^{2}}{e}}\left[1-{\dfrac {d\,(f_{i,\,1}+e)-f_{i,\,2}^{2}}{d\,(f_{i,\,1}+e)+{\dfrac {f_{i,\,2}^{2}\,f_{i,\,1}}{e}}}}\right]={\dfrac {f_{i,\,1}^{2}}{e}}\;{\dfrac {f_{i,\,2}^{2}\left(1+{\dfrac {f_{i,\,1}}{e}}\right)}{d\,(f_{i,\,1}+e)+{\dfrac {f_{i,\,2}^{2}\,f_{i,\,1}}{e}}}}\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d87b79cc9a7dc9eb2b57b30de30f068ad8bca849)













![{\displaystyle \;43\equiv 6^{2}\!\!{\pmod {7}}\;\ldots {\big ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/367d8a80b995dc2cdf16e8f7872a85d3a380e120)





















![{\displaystyle \;n\;\sin(\varepsilon )=\sin \!\left[r(\varepsilon )\right]\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eaa9225161a9ce814691802920488f12ddebb123)
![{\displaystyle \;\sin \!\left[r(\varepsilon )\right]\simeq n\;\varepsilon \;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32fbe822cdbe68abce2200fbd637b24c0b46333d)









![{\displaystyle \;\tan \!\left[(n-1)\;\varepsilon \right]={\dfrac {H(\varepsilon )I(\varepsilon )}{\overline {H(\varepsilon )A_{i}(\varepsilon )}}}\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/da8043c54b2f01ef7fac4b7f9a6e9d2283610cb4)
![{\displaystyle \;{\dfrac {\sin \!\left[(n-1)\;\varepsilon \right]}{\cos \!\left[(n-1)\;\varepsilon \right]}}\simeq }](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5835ed79e1eb59533115f9db31cff714a425875)






![{\displaystyle \;\sin \!\left[r(\varepsilon )\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b1ca88a31a8fa10eddefebab83738f2b101e0a9)

















![{\displaystyle \;\left[OA_{o}\right]>\left[OF_{o}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/545543a378329db84262bbeed9335b3f13eee059)
![{\displaystyle \;\left[OA_{o}\right]\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/44bb210c10c097e94d64be29a5eecc593abdcf65)
![{\displaystyle \;\left[OA_{o}\right]<\left[OF_{o}\right]{\Big )}\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f9ec94be869f537b4f3c92838aebcfcf1b2026b)

![{\displaystyle \;\left[OA_{o}\right]<\left[OF_{o}\right]\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/420f91d2d901c125ea15e57cca4e7449bdeae5aa)
![{\displaystyle \;\left[OA_{o}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5222e0e0839493b8a85e417448986fddcdf0019f)
![{\displaystyle \;\left[OA_{o}\right]>\left[OF_{o}\right]{\Big )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/374594ac6d0ebf701426fa73b8a0d76d1baac2ce)

![{\displaystyle \;\left[OA_{i}\right]>\left[OF_{i}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97b8866963b379a03354c8288a20b56a43e949e9)
![{\displaystyle \;\left[OA_{i}\right]\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aee6b552a578ea4bbbda6a018836784e7f1dec4f)
![{\displaystyle \;\left[OA_{i}\right]<\left[OF_{i}\right]{\Big )}\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c231eb3d295c701e2f1df2116365c7e718ae31f)

![{\displaystyle \;\left[OA_{i}\right]>\left[OF_{i}\right]{\Big )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e444d5aff558e13383b883d237c89ada0044280d)






![{\displaystyle {\bigg ]}\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9d9e51d2d3cafc3e7d1a34196d9b65ac61640ed1)


![{\displaystyle {\bigg ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6515d4ab3aeccb7f846142fd40a7d0f7d1129e6e)
























![{\displaystyle \;f_{i}>0{\big ]}\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a83dee786e6ef69a66dae81386e38b38ee1b593)

![{\displaystyle \;F_{i}\;{\big (}\sigma _{i}>0{\big )}{\big ]}\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c2278d47e5a10f9c40e255a0e9b1f5595f95dadb)

![{\displaystyle \;f_{i}<0{\big ]}\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f1c6e84b13909684956eb6f86062966ac5ace6f)

![{\displaystyle \;F_{i}\;{\big (}\sigma _{i}<0{\big )}{\big ]}\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2853aded545fde721067366c595183f74e2ee815)




![{\displaystyle {\big )}{\big ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0fd0c02f32f607a22fbd5b1388a07b45e1c3f614)






![{\displaystyle \;\left({\dfrac {\partial \left[\vert G_{t,\,1}(A_{o})\vert \right]}{\partial f_{i}}}\right)_{\!\!D}=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3368f4a19e270ace41d79bd670f944520e062d41)
![{\displaystyle {\dfrac {\left[D-{\sqrt {D\left(D-4\;f_{i}\right)}}\right]{\dfrac {-4\;D}{2\;{\sqrt {D\left(D-4\;f_{i}\right)}}}}-\left[D+{\sqrt {D\left(D-4\;f_{i}\right)}}\right]{\dfrac {4\;D}{2\;{\sqrt {D\left(D-4\;f_{i}\right)}}}}}{\left[D-{\sqrt {D\left(D-4\;f_{i}\right)}}\right]^{2}}}\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3cfed6899d6f9c3c534839918eeeb95c1e4ac1f2)
![{\displaystyle \;\left({\dfrac {\partial \left[\vert G_{t,\,1}(A_{o})\vert \right]}{\partial f_{i}}}\right)_{\!\!D}={\dfrac {-4\;D^{2}}{{\sqrt {D\left(D-4\;f_{i}\right)}}\left[D-{\sqrt {D\left(D-4\;f_{i}\right)}}\right]^{2}}}<0\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/138c859faf819a844c7c3b06844203d4edd7dbd4)
![{\displaystyle \;\left({\dfrac {\partial [|G_{t,\,1}(A_{o})|]}{\partial D}}\right)_{\!\!f_{i}}=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca174c64e65bc1cd7c9edecb047a872092698dcf)
![{\displaystyle {\dfrac {\left[D-{\sqrt {D\left(D-4\;f_{i}\right)}}\right]\left[1+{\dfrac {2\;D-4\;f_{i}}{2\;{\sqrt {D\left(D-4\;f_{i}\right)}}}}\right]-\left[D+{\sqrt {D\left(D-4\;f_{i}\right)}}\right]\left[1-{\dfrac {2\;D-4\;f_{i}}{2\;{\sqrt {D\left(D-4\;f_{i}\right)}}}}\right]}{\left[D-{\sqrt {D\left(D-4\;f_{i}\right)}}\right]^{2}}}\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd72eb11ea722ea474204f4218f2e8fcc0be611b)
![{\displaystyle \;\left({\dfrac {\partial [|G_{t,\,1}(A_{o})|]}{\partial D}}\right)_{\!\!f_{i}}={\dfrac {4\;D\;f_{i}}{{\sqrt {D\left(D-4\;f_{i}\right)}}\left[D-{\sqrt {D\left(D-4\;f_{i}\right)}}\right]^{2}}}>0\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4bca6304d162668d8a50592c4f82a09d64d9c06e)






























