Trigonométrie/Annexe/Cercle trigonométrique et radians

Le cercle trigonométrique

Le cercle trigonométrique.

Définition

Dans un repère orthonormé, on appelle cercle trigonométrique le cercle ayant pour centre l'origine du repère et pour rayon 1.

• Nous poserons comme orientation le sens inverse des aiguilles d'une montre, appelé sens trigonométrique direct.
• L'origine dite « de décompte angulaire » sera le point I d'abscisse 1 et l'unité de longueur va être la même que celle du repère.

Les angles en radians

Définition

Soit M un point quelconque du cercle trigonométrique. Une mesure en radians de l'angle orienté $({\overrightarrow {OI}},{\overrightarrow {OM}})$ est la longueur de l'arc ${\overset {\curvearrowright }{IM}}$, comptée positivement dans le sens direct et négativement dans le sens indirect

Exemple

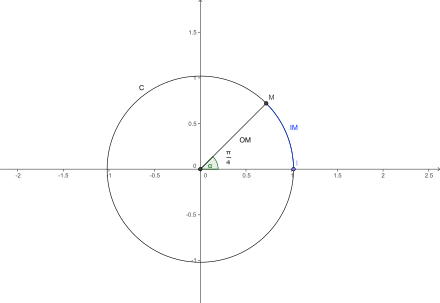
Dans la figure ci-contre, le point $M$ est tel que l'angle ${\widehat {IOM}}$ vaut 45 degrés. L'arc ${\overset {\curvearrowright }{IM}}$ a pour longueur le huitième de la circonférence du cercle : $2\pi$, c'est-à-dire ${\frac {\pi }{4}}$.

L'angle orienté $({\overrightarrow {OI}},{\overrightarrow {OM}})$ a donc pour mesure en radians ${\frac {\pi }{4}}$.

Elle est positive car cet arc est orienté dans le sens positif.

Nous pouvons aussi placer sans grandes difficultés $\pi ,\ {\frac {\pi }{2}},\ {\frac {\pi }{3}},\ {\frac {\pi }{4}}\dots$.

Un angle possède une infinité de mesures

La notion de mesure d'un angle peut être étendue à des nombres supérieurs à $2\pi$ (c'est-à-dire supérieurs à 360°).

Par exemple : mesure de 100 radians, il faut imaginer une ficelle de 100 unités qui s'enroulerait autour du cercle trigonométrique dans le sens direct.

Propriété

Les différentes mesures d'un angle se déduisent les unes des autres en ajoutant ou en retranchant un certain nombre de fois $2\pi$.

Il y a donc une périodicité de $2\pi$.

Exemples

• Sur le cercle trigonométrique, les valeurs $0$ et $2\pi$ se trouvent confondues.

  Il en est d'ailleurs de même pour $2\pi ,\ 4\pi ,-2\pi ,\ -4\pi \dots$.

• L'angle de mesure ${\frac {\pi }{5}}$ a aussi pour mesure ${\frac {11\pi }{5}}$ ainsi que $-{\frac {9\pi }{5}}$, ${\frac {21\pi }{5}}$ ou $-{\frac {19\pi }{5}}$.

Mesure principale

Définition

La mesure comprise dans l'intervalle $]-\pi ,\pi ]$ est la mesure principale de ${\overset {\scriptstyle \curvearrowright }{AB}}$.

Elle correspond à la longueur (en valeur algébrique) du chemin le plus court reliant $A$ à $B$.

Dans l'exemple précédent, la mesure principale est ${\frac {\pi }{5}}$.

Conversion degrés-radians

La conversion degrés-radians se fait facilement en utilisant les formules :

Propriété

• ${\text{Angle en deg}}={\frac {180}{\pi }}\times {\text{angle en rad}}$.
• ${\text{Angle en rad}}={\frac {\pi }{180}}\times {\text{angle en deg}}$.

La figure ci-dessous donne quelques correspondances à connaître :