Intégrales en physique/Découpages classiques

Début de la boite de navigation du chapitre

fin de la boite de navigation du chapitre

Intégration sur un disque

Du fait de la symétrie du disque, les coordonnées polaires sont les plus adaptées. On considère une grandeur f(r,θ) dont on veut calculer l'influence F sur la totalité de la surface Σ du disque.

Secteur angulaire

La surface élémentaire d'ordre 2 d²S la plus simple à exprimer est celle située en un point de coordonnées (r,θ) :

• qui s'étend radialement sur une longueur dr
• qui balaie un angle dθ

Si, du fait des très petites dimensions de la surface, on peut assimiler d²S à un rectangle de dimensions dr et r dθ, on obtient $\mathrm {d} ^{2}S=\mathrm {d} r~r\mathrm {d} \theta$.

On peut vérifier qu'on retombe bien sur l'aire de Σ en sommant les surfaces élémentaires :

${\begin{aligned}\int _{r=0}^{r=R}\int _{\theta =0}^{\theta =2\pi }\mathrm {d} ^{2}S&=\int _{r=0}^{r=R}\int _{\theta =0}^{\theta =2\pi }r\,\mathrm {d} r\,\mathrm {d} \theta \\&=\int _{r=0}^{r=R}r\,\mathrm {d} r\,\int _{\theta =0}^{\theta =2\pi }\mathrm {d} \theta \\&=\left[{\frac {r^{2}}{2}}\right]_{r=0}^{r=R}\times 2\pi \\&=\pi R^{2}={\mathcal {A}}_{\Sigma }\end{aligned}}$

F vaut alors $F=\int _{r=0}^{r=R}\int _{\theta =0}^{\theta =2\pi }f(r,\theta )\,r\,\mathrm {d} r\,\mathrm {d} \theta$

Couronne élémentaire

Si de plus, f ne dépend pas de θ : $F=\int _{\theta =0}^{\theta =2\pi }\mathrm {d} \theta \int _{r=0}^{r=R}f(r)\,r\,\mathrm {d} r=2\pi \int _{r=0}^{r=R}f(r)\,r\,\mathrm {d} r$

Cela revient à choisir une surface élémentaire en forme de couronne située à une distance r du centre, de largeur infinitésimale dr.

Si on « coupe » cette couronne et qu'on la « déroule » par la pensée, on peut supposer que son aire est assimilable à celle d'un rectangle de longueur 2πr (la circonférence d'un cercle de rayon r) et de largeur dr.

On obtient alors une couronne infinitésimale d'ordre 1 d'aire $\mathrm {d} S=2\pi r~\mathrm {d} r$.

On peut vérifier qu'on retombe bien sur l'aire de Σ en sommant les couronnes élémentaires :

${\begin{aligned}\int _{r=0}^{r=R}\mathrm {d} S&=\int _{r=0}^{r=R}2\pi r\,\mathrm {d} r\\&=\left[{\frac {r^{2}}{2}}\right]_{r=0}^{r=R}\times 2\pi \\&=\pi R^{2}={\mathcal {A}}_{\Sigma }\end{aligned}}$

F vaut alors $F=2\pi \int _{r=0}^{r=R}r\,f(r)\mathrm {d} r$

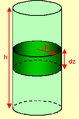
Intégration sur un cylindre

• 
  $\mathrm {d} S=2\pi R\,\mathrm {d} z$
• 
  $\mathrm {d} V=2\pi rh\,\mathrm {d} r$

Intégration sur une sphère

Élément infinitésimal d'ordre 2

$\mathrm {d} ^{2}S=R^{2}\sin(\varphi )\,{\rm {d\theta {\rm {d\varphi }}}}$

Intégration sur des couronnes

$\mathrm {d} S=2\pi R^{2}\sin(\theta )\,\mathrm {d} \theta$

Intégration sur une boule

• $\mathrm {d} V=4\pi r^{2}\,\mathrm {d} r$