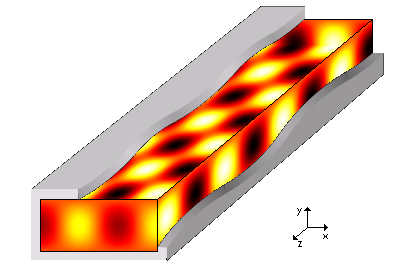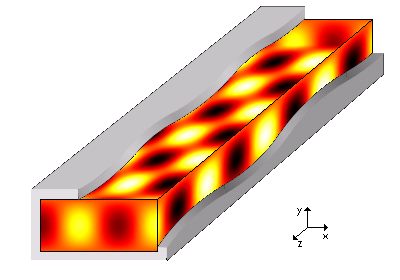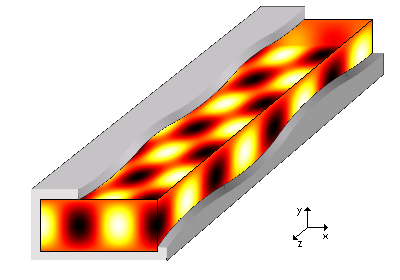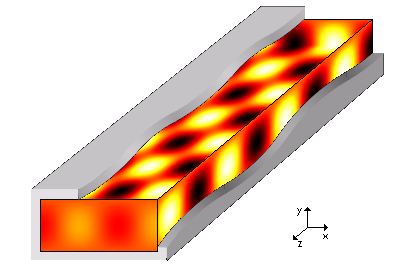
Ondes électromagnétiques guidées/Guide rectangulaire

Début de la boite de navigation du chapitre

fin de la boite de navigation du chapitre

Dans ce chapitre, ${\mathcal {G}}$ est un guide d'ondes :

• de section droite rectangulaire $(0<x<a~,~0<y<b)$
• supposé illimité dans la direction ${\vec {u}}_{z}$
• parfaitement conducteur
• creux

On souhaite propager dans ce guide une onde de pulsation ω. Son vecteur d'onde dans le vide a pour norme $k_{0}={\frac {\omega }{c}}$ et sa longueur d'onde dans le vide est $\lambda _{0}={\frac {2\pi c}{\omega }}$.

On ne s'intéressera dans cette page qu’à la propagation des modes TE.

Étude des modes TE_m0

Quantification

Supposons dans un premier temps le champ électrique polarisé rectilignement suivant ${\vec {u}}_{y}$.

${\vec {E}}=E(x,y)e^{j(kz-\omega t)}{\vec {u}}_{y}$

On a vu que ce champ satisfaisait :

• l'équation ${\rm {div}}({\vec {E}})=0$
• l'équation d'Helmotz ${\vec {\Delta }}{\vec {E}}+{\frac {\omega ^{2}}{c^{2}}}{\vec {E}}={\vec {0}}$
• les conditions aux limites. Le champ électrique étant suivant la direction ${\vec {u}}_{y}$, on a ${\begin{cases}\sigma (x=0)=0\\\sigma (x=a)=0\end{cases}}$. Les équations de passage du champ électrique assurent alors que ${\begin{cases}{\vec {E}}(x=0)={\vec {0}}\\{\vec {E}}(x=a)={\vec {0}}\end{cases}}$

On en tire les conclusions suivantes :

• Du premier point, on tire ${\frac {\partial E(x,y)}{\partial y}}=0$, ce qui permet de se ramener à ${\vec {E}}=E(x)e^{j(kz-\omega t)}{\vec {u}}_{y}$
• La réinjection de ce premier résultat dans le deuxième point donne l'équation différentielle vérifiée par $E(x)~:~{\frac {\partial ^{2}E(x)}{\partial x^{2}}}+k_{\perp }^{2}E(x)=0$

La résolution de cette équation différentielle donne des solutions de la forme $E(x)=C_{1}\sin(k_{\perp }x)+C_{2}\cos(k_{\perp }x)$

• La condition aux limites ${\vec {E}}(x=0)={\vec {0}}$ impose $C_{2}=0$

La condition aux limites $E(x=a)={\vec {0}}$ impose $\exists m\in \mathbb {N} ^{*},~k_{\perp }a=m\pi$

Finalement, le champ électrique a pour expression ${\vec {E}}=E_{0y}\sin \left({\frac {m\pi }{a}}x\right)e^{j(kz-\omega t)}{\vec {u}}_{y},~m\in \mathbb {N} ^{*}$.

Propriétés du champ électrique propagé

Le champ électrique est donc :

• progressif dans la direction ${\vec {u}}_{z}$
• stationnaire dans la direction ${\vec {u}}_{x}$
• quantifié par un entier m. Chaque valeur de m définit un mode, noté TE_m0.
• indépendant en module de z. Ceci est dû à l'hypothèse de conducteur parfait, qui aboutit à une atténuation nulle.

Fondamental

Si $a>b$, le mode TE₁₀ est appelé fondamental.

Dispersion et coupure

La quantification $k_{\perp }={\frac {m\pi }{a}},~m\in \mathbb {N} ^{*}$ donne, pour un entier $m\in \mathbb {N} ^{*}$ donné, la relation de dispersion $k^{2}={\frac {\omega ^{2}}{c^{2}}}-\left({\frac {m\pi }{a}}\right)^{2}$

Les modes propagés ont pour pulsation $\omega _{m0}=c{\sqrt {k^{2}+\left({\frac {m\pi }{a}}\right)^{2}}}$

Début d’un théorème

Dispersion et coupure dans un guide d'ondes rectangulaire pour les modes TE_m0

Posons $(\omega _{m0})_{c}={\frac {m\pi c}{a}}$.

La relation de dispersion devient $k^{2}={\frac {\omega ^{2}-(\omega _{m0})_{c}^{2}}{c^{2}}}$. Pour des valeurs de ω inférieures à $(\omega _{m0})_{c}$, on a $k^{2}<0$ et on obtient une onde évanescente. $(\omega _{m0})_{c}$ joue donc le rôle de pulsation de coupure du guide d'ondes pour le mode TE_m0, qui se comporte comme un filtre passe-haut.

On remarque également que le guide d'onde est dispersif.

Fin du théorème

Vitesse de phase, vitesse de groupe

Pour $\omega >(\omega _{m0})_{c}$, une onde progressive est susceptible de se propager.

• La vitesse de phase vaut $v_{\varphi }={\frac {\omega }{k}}={\frac {c}{\sqrt {1-\left({\frac {(\omega _{m0})_{c}}{\omega }}\right)^{2}}}}$
• La vitesse de groupe vaut $v_{g}={\frac {{\rm {d}}\omega }{{\rm {d}}k}}=c{\sqrt {1-\left({\frac {(\omega _{m0})_{c}}{\omega }}\right)^{2}}}$

La vitesse de groupe est inférieure à c. La propagation est donc plus lente dans un guide que dans le vide.

Interprétation géométrique

Pour propager une onde électromagnétique dans le guide, il faut $\omega >(\omega _{m0})_{c}$. Il existe alors $\theta \in \left]0;{\frac {\pi }{2}}\right[$ tel que $\cos(\theta )={\frac {(\omega _{m0})_{c}}{\omega }}$.

On a $\cos(\theta )={\frac {(\omega _{m0})_{c}}{\omega }}={\frac {m\pi c}{a\omega }}={\frac {m\pi }{ak_{0}}}={\frac {k_{\perp }}{k_{0}}}$.

Tout se passe donc comme si l’on décomposait le vecteur d'onde ${\vec {k}}_{0}$ suivant deux composantes :

• la composante suivant ${\vec {u}}_{x}$, transversale par rapport à la direction de propagation de l'onde, notée ${\vec {k}}_{\perp }$
• la composante suivant ${\vec {u}}_{z}$, parallèle à la direction de propagation de l'onde, notée ${\vec {k}}_{/\!/}$

Les normes de ces vecteurs vérifient de plus ${\begin{cases}k_{\perp }=k_{0}\cos(\theta )\\k_{/\!/}=k_{0}\sin(\theta )\end{cases}}$

L'angle θ est alors équivalent à l'angle d'incidence de l'onde sur le guide. Cette vision des choses permet de retomber sur les résultats montrés plus tôt :

• Dans la direction ${\vec {u}}_{z}$, on a une onde progressive de vecteur d'onde ${\vec {k}}_{/\!/}$. Sa vitesse de phase est $v_{\varphi }={\frac {\omega }{k_{/\!/}}}={\frac {c}{\sin(\theta )}}$
• Dans la direction ${\vec {u}}_{x}$, on obtient une onde stationnaire de vecteur d'onde ${\vec {k}}_{\perp }$ quantifié.

Remarque très importante

Il est très important de remarquer que :

• dans le terme en $e^{j(kz-\omega t)}$ du champ électromagnétique propagé dans le guide
• dans l’expression de la vitesse de phase $v_{\varphi }={\frac {\omega }{k}}$

le k dont il est question est en réalité à chaque fois la composante longitudinale $k_{/\!/}$ du vecteur d'onde total, et non la norme du vecteur ${\vec {k}}={\vec {k}}_{/\!/}+{\vec {k}}_{\perp }$.

Dans la suite de ce cours, on prendra donc la liberté de conserver le raccourci k pour ne pas alourdir les notations, mais il faut garder en tête que c’est un abus de notation.

Quantification des incidences

Si on poursuit l'approche géométrique du paragraphe précédent, étudions l'influence de θ sur la propagation. Pour une onde de pulsation ω déterminée :

$\cos(\theta )={\frac {m\pi c}{a\omega }}={\frac {m\lambda _{0}}{2a}}$.

Début d’un théorème

Quantification des inclinaisons

* Seules certaines valeurs de θ sont autorisées.

• Pour des fréquences trop faibles (ie des longueurs d'onde trop grandes), il n'existe aucune inclinaison possible pour propager l'onde.

On obtient donc une longueur d'onde de coupure $\lambda _{c}=2a$, ie une pulsation de coupure $\omega _{c}={\frac {\pi c}{a}}$ qui correspond à la fréquence de coupure du fondamental. Dans ce cas limite, on n'a qu'une onde stationnaire qui ne se propage pas suivant ${\vec {u}}_{z}$.

Fin du théorème

Si on souhaite propager un signal polychromatique dans un certain mode TE_m0, à chaque fréquence correspond une incidence donnée. Chaque fréquence se propage alors dans le guide « suivant ses propres zigzags », et donc à des vitesses suivant ${\vec {u}}_{z}$ différentes. Ceci explique le phénomène de dispersion.

Étude des modes TE_0n

Supposons à présent le champ électrique polarisé rectilignement suivant ${\vec {u}}_{x}$. De la même manière que précédemment, on obtient que ce champ est :

• progressif dans la direction ${\vec {u}}_{z}$
• stationnaire dans la direction ${\vec {u}}_{y}$
• quantifié par un entier n. Chaque valeur de n définit un mode.
• indépendant en module de z.

${\vec {E}}=E_{0x}\sin \left({\frac {n\pi }{b}}y\right)e^{j(kz-\omega t)}{\vec {u}}_{x},~n\in \mathbb {N} ^{*}$

Étude des modes TE_mn

Cherchons à présent la forme d'un champ électrique propagé de direction quelconque. En mode TE, tout champ électrique propagé est la superposition d'un champ électrique suivant ${\vec {u}}_{x}$ et d'un champ électrique suivant ${\vec {u}}_{y}$. En effectuant la superposition des résultats obtenus aux paragraphes précédents dans le cas le plus général, on subodore au final une double quantification des champs électriques transversaux.

Note : Pour trouver l’expression analytique de ces modes supérieurs, il faut reprendre depuis le début le système des équations vérifiées par E_x et E_y, et résoudre ce système par la méthode de séparation des variables. Vous pouvez essayer de faire ces calculs pour vous entraîner à la résolution de ce type de problème. On peut également retrouver directement tous ces résultats en partant des fonctions génératrices, ce qui est proposé en exercice.

Faites ces exercices : Application des fonctions génératrices à l'étude du guide d'ondes rectangulaire.

Quantification des modes TE en guide d'ondes rectangulaire

Les modes TE d'un guide d'ondes rectangulaires sont quantifiés par deux entiers :

• un entier m indique le nombre de demi-périodes spatiales des champs suivant l'axe x
• un entier n indique le nombre de demi-périodes spatiales des champs suivant l'axe y

Pour deux entiers m et n donnés, on parle de mode TE_mn.

Début de l'exemple

Mode TE₃₁

L'animation ci-dessous montre la configuration et la propagation de la composante E_x du champ électromagnétique du mode TE₃₁.

À noter que :

• Suivant l'axe des x, le champ E_x fait 3 demi-périodes
• Suivant l'axe des y, le champ E_x fait 1 demi-période

Fin de l'exemple

On peut alors de la même manière que précédemment décomposer le vecteur d'onde en 2 composantes :

• Dans la direction ${\vec {u}}_{z}$, un vecteur d'onde ${\vec {k}}_{/\!/}$ représentant une onde progressive.
• Dans la direction orthogonale à ${\vec {u}}_{z}$, un vecteur d'onde ${\vec {k}}_{\perp }$ représentant une onde stationnaire.

Le vecteur d'onde ${\vec {k}}_{\perp }$ est de norme quantifiée $k_{\perp }^{2}=\left({\frac {m\pi }{a}}\right)^{2}+\left({\frac {n\pi }{b}}\right)^{2},~(n,m)\in (\mathbb {N} ^{*})^{2}$

La relation de dispersion devient :

$k^{2}=k_{0}^{2}-k_{\perp }^{2}={\frac {\omega ^{2}}{c^{2}}}-\left({\frac {m\pi }{a}}\right)^{2}-\left({\frac {n\pi }{b}}\right)^{2}$

Les modes propagés ont alors pour pulsation:

$\omega _{mn}=c{\sqrt {k^{2}+\left({\frac {m\pi }{a}}\right)^{2}+\left({\frac {n\pi }{b}}\right)^{2}}}$

Début d’un théorème

Dispersion et coupure dans un guide d'ondes rectangulaire pour les modes TE_mn

La pulsation de coupure du mode TE_mn est $(\omega _{mn})_{c}=c{\sqrt {\left({\frac {m\pi }{a}}\right)^{2}+\left({\frac {n\pi }{b}}\right)^{2}}}$ La relation de dispersion devient $k^{2}={\frac {\omega ^{2}-(\omega _{mn})_{c}}{c^{2}}}$.

Fin du théorème