En raison de limitations techniques, la typographie souhaitable du titre, «
Exercice : Divers
Intégration en mathématiques/Exercices/Divers », n'a pu être restituée correctement ci-dessus.
Pour  et
et  entiers naturels, on considère l'intégrale :
entiers naturels, on considère l'intégrale :
 .
.
1° Calculer  :
:
- a) en utilisant le changement de variable
 et la formule du binôme ;
et la formule du binôme ;
- b) en établissant, par intégration par parties, une relation de récurrence entre
 et
et  , puis en déduisant
, puis en déduisant  du calcul de
du calcul de  .
.
2° Déduire de ce qui précède que :
 .
.
Solution
-
 .
.- Si
 ,
, ![{\displaystyle I(m,n)={\frac {1}{m+1}}\underbrace {\left[(x-a)^{m+1}(b-x)^{n}\right]_{a}^{b}} _{0}+{\frac {n}{m+1}}\,I(m+1,n-1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8792532f947e085c8a56bcab469af56a24203db6) .
.
Or  .
.
Donc  .
.
- Immédiat.
Soit :
 .
.
Prouver que, pour tout  :
:
 .
.
Solution

![{\displaystyle \left[{\frac {x^{3}}{3}}+ax\right]_{x^{2}>-a,\,0<x<1}-\left[{\frac {x^{3}}{3}}+ax\right]_{x^{2}<-a,\,0<x<1}=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ffcd290eec0de22e314bbbc74b401af2ad0d334c)
![{\displaystyle {\begin{cases}{\text{si}}&a\leq -1&:&-\left[{\frac {x^{3}}{3}}+ax\right]_{0}^{1}=-a-{\frac {1}{3}}\\{\text{si}}&-1\leq a\leq 0&:&\left[{\frac {x^{3}}{3}}+ax\right]_{\sqrt {-a}}^{1}-\left[{\frac {x^{3}}{3}}+ax\right]_{0}^{\sqrt {-a}}=a+{\frac {1}{3}}+{\frac {4(-a)^{3/2}}{3}}\\{\text{si}}&a\geq 0&:&\left[{\frac {x^{3}}{3}}+ax\right]_{0}^{1}=a+{\frac {1}{3}}\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/974d4f0073e1a0a6c7f6243a91ccf83b34ea689a)
(dans chacun des deux cas  ou
ou  , communs à deux expressions, les deux fonctions de
, communs à deux expressions, les deux fonctions de  coïncident).
coïncident).
Cette fonction  est décroissante sur
est décroissante sur ![{\displaystyle \left]-\infty ,-{\frac {1}{4}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1084dd18be4415cc93b7b9d3d01cf43d91d23b6a) et croissante sur
et croissante sur  .
.
On considère, dans un repère orthonormal, la courbe  d'équation :
d'équation :
 .
.
Soit  un nombre strictement positif. On désigne par
un nombre strictement positif. On désigne par  et
et  les deux points de la courbe
les deux points de la courbe  d'abscisses respectives
d'abscisses respectives  et
et  , et
, et  et
et  leurs projetés orthogonaux sur l’axe des abscisses.
leurs projetés orthogonaux sur l’axe des abscisses.
1° Calculer l’aire  de la surface limitée par l’axe des abscisses, les droites
de la surface limitée par l’axe des abscisses, les droites  et
et  et la courbe
et la courbe  .
.
2° On considère la fonction  définie par :
définie par :

- Calculer la dérivée de la fonction
 pour
pour 
- Étudier la variation de
 et construire son graphique.
et construire son graphique.
- Préciser les demi-tangentes à ce graphique au point d'abscisse
 .
.
3° Calculer les valeurs de  pour lesquelles l'aire
pour lesquelles l'aire  est égale à
est égale à  .
.
4° Étudier les limites à droite et à gauche en  de la fonction :
de la fonction :
 .
.
Solution
![{\displaystyle S(x)=\left|\int _{x}^{\mathrm {e} ^{2}/x}{\frac {1}{t}}\,\mathrm {d} t\right|=\left|[\ln ]_{x}^{\mathrm {e} ^{2}/x}\right|=2\left|1-\ln x\right|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a500c6ff21bf56dc3146fb04668ad3466c141d8) .
. si
si  et
et  si
si  donc
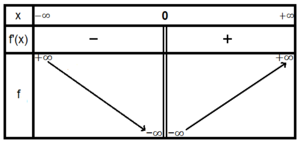
donc  est décroissante sur
est décroissante sur ![{\displaystyle \left]0,\mathrm {e} \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1164de38fc1c22e2c1896ac27a5e28164d464570) et croissante sur
et croissante sur  . En
. En  et en
et en  , elle tend vers
, elle tend vers  .
.
Le graphique de S est donné par ;

Les deux demi-tangentes au point  ont pour équations
ont pour équations  et
et  .
. ou
ou  .
.- Quand
 ,
,  et quand
et quand  ,
,  .
.
On considère la fonction  définie par :
définie par :
 .
.
1° Étudier son ensemble de définition, démontrer qu'elle est périodique de période  et étudier sa variation dans l'intervalle
et étudier sa variation dans l'intervalle ![{\displaystyle \left]-{\frac {\pi }{4}},\,{\frac {3\pi }{4}}\right[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c89744e25c24e8a0f990cdd73e263f122b3721b8) .
.
- Tracer la courbe représentative de
 dans un repère orthonormal.
dans un repère orthonormal.
2° Calculer les primitives de  . On pourra mettre
. On pourra mettre  sous la forme :
sous la forme :

- où
 et
et  sont des constantes à préciser.
sont des constantes à préciser.
- En déduire la valeur de l’aire du domaine compris entre la courbe, l'axe des abscisses et les deux droites d'équations
 ,
,  .
.
Soit la fonction  définie par :
définie par :
 .
.
1° Étudier la variation de  et la représenter graphiquement par rapport à un repère orthonormal
et la représenter graphiquement par rapport à un repère orthonormal  . Soit
. Soit  , la courbe représentative.
, la courbe représentative.
2° Écrire l'équation de la tangente à  au point
au point  ayant pour abscisse le nombre
ayant pour abscisse le nombre  .
.
3° Vérifier que la fonction  définie par :
définie par :

- est une primitive de la fonction
 dans chacun des intervalles où cette dernière est définie.
dans chacun des intervalles où cette dernière est définie.
4° Évaluer l’aire du domaine plan délimité par l'axe des abscisses, la courbe  et la tangente à
et la tangente à  au point
au point  .
.















![{\displaystyle I(m,n)={\frac {1}{m+1}}\underbrace {\left[(x-a)^{m+1}(b-x)^{n}\right]_{a}^{b}} _{0}+{\frac {n}{m+1}}\,I(m+1,n-1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8792532f947e085c8a56bcab469af56a24203db6)






![{\displaystyle \left[{\frac {x^{3}}{3}}+ax\right]_{x^{2}>-a,\,0<x<1}-\left[{\frac {x^{3}}{3}}+ax\right]_{x^{2}<-a,\,0<x<1}=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ffcd290eec0de22e314bbbc74b401af2ad0d334c)
![{\displaystyle {\begin{cases}{\text{si}}&a\leq -1&:&-\left[{\frac {x^{3}}{3}}+ax\right]_{0}^{1}=-a-{\frac {1}{3}}\\{\text{si}}&-1\leq a\leq 0&:&\left[{\frac {x^{3}}{3}}+ax\right]_{\sqrt {-a}}^{1}-\left[{\frac {x^{3}}{3}}+ax\right]_{0}^{\sqrt {-a}}=a+{\frac {1}{3}}+{\frac {4(-a)^{3/2}}{3}}\\{\text{si}}&a\geq 0&:&\left[{\frac {x^{3}}{3}}+ax\right]_{0}^{1}=a+{\frac {1}{3}}\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/974d4f0073e1a0a6c7f6243a91ccf83b34ea689a)



![{\displaystyle \left]-\infty ,-{\frac {1}{4}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1084dd18be4415cc93b7b9d3d01cf43d91d23b6a)



















![{\displaystyle S(x)=\left|\int _{x}^{\mathrm {e} ^{2}/x}{\frac {1}{t}}\,\mathrm {d} t\right|=\left|[\ln ]_{x}^{\mathrm {e} ^{2}/x}\right|=2\left|1-\ln x\right|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a500c6ff21bf56dc3146fb04668ad3466c141d8)




![{\displaystyle \left]0,\mathrm {e} \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1164de38fc1c22e2c1896ac27a5e28164d464570)
















![{\displaystyle \left]-{\frac {\pi }{4}},\,{\frac {3\pi }{4}}\right[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c89744e25c24e8a0f990cdd73e263f122b3721b8)







![{\displaystyle \left]-{\frac {\pi }{4}}+k\pi ,{\frac {3\pi }{4}}+k\pi \right[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/31789e2138fde6c2d3a443b4cfab38a3d19ec3cf)










![{\displaystyle \int _{0}^{\frac {\pi }{2}}f(x)\,\mathrm {d} x=\left[{\frac {x}{2}}-{\frac {1}{2}}\ln \left|\cos x+\sin x\right|\right]_{0}^{\frac {\pi }{2}}=\left[{\frac {x}{2}}\right]_{0}^{\frac {\pi }{2}}={\frac {\pi }{4}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/895830c9a94729dd7ea11b66d6e37b36f80757ea)
















![{\displaystyle \mathrm {e} -\int _{1}^{\mathrm {e} }f(x)\,\mathrm {d} x=\mathrm {e} -\left[x\ln \left(x^{2}\right)-2x\right]_{1}^{\mathrm {e} }=\mathrm {e} -2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba30fb1b60fdac726901f12b9dead18875e00779)