En raison de limitations techniques, la typographie souhaitable du titre, «
Exercice : Calculs d'aires 2
Intégration en mathématiques/Exercices/Calculs d'aires 2 », n'a pu être restituée correctement ci-dessus.
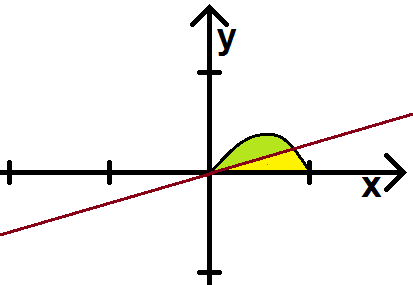
Évaluer l’aire du sous-ensemble plan délimité par les courbes d'équations :
 .
.
Solution
![{\displaystyle 1+\int _{1}^{4}\left({\frac {1}{x}}+{\frac {1}{x^{2}}}\right)\,\mathrm {d} x=1+\left[\ln x-{\frac {1}{x}}\right]_{1}^{4}={\frac {7}{4}}+\ln 4}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc29f39dc9bc869bbcef1c8ea93dce08b754ae77) .
.
Évaluer l’aire du sous-ensemble plan délimité par les courbes d'équations :
 .
.
Solution
![{\displaystyle \int _{-{\frac {\pi }{4}}}^{0}(\cos -\tan )=\left[\sin +\ln |\cos |\right]_{-{\frac {\pi }{4}}}^{0}={\frac {{\sqrt {2}}+\ln 2}{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/107c568c0a7d767cf690eb755031a98e54abf02f)
Soit  la fonction définie par :
la fonction définie par :
 .
.
1° Étudier  et en faire une représentation graphique
et en faire une représentation graphique  .
.
2° Calculer l’aire du sous-ensemble plan délimité par  et l’axe des abscisses du repère.
et l’axe des abscisses du repère.
Solution
 est définie sur
est définie sur ![{\displaystyle \left[-4,4\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2054bdf8d576d3729a4a5e6f2dd30765e74c527e) et paire, donc il suffit de l'étudier sur
et paire, donc il suffit de l'étudier sur ![{\displaystyle \left[0,4\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd04af5bb35776de469be99e538a5cc93c2c90bb) . Sur
. Sur ![{\displaystyle \left]0,4\right[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/042a5c9cec5e492d4d78e4efb5628ac5233bee54) ,
,  donc
donc  est strictement décroissante sur
est strictement décroissante sur ![{\displaystyle \left[0,4\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd04af5bb35776de469be99e538a5cc93c2c90bb) , de
, de  à
à  .
.
Le reste de l'étude s'obtient par parité et l'on obtient le tableau de variation suivant :

La courbe représentative (symétrique par rapport à l'axe des ordonnées) de la fonction  est :
est :

![{\displaystyle \int _{-4}^{4}f=2\left[{\frac {2(4+x)^{3/2}}{3}}-{\frac {2(4-x)^{3/2}}{3}}-2x{\sqrt {2}}\right]_{0}^{4}={\frac {16{\sqrt {2}}}{3}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b981f34886ba223036d8a1ba6893f40fd53dea7c) .
.
Soit  la fonction définie par :
la fonction définie par :
 .
.
1° Étudier  et en faire une représentation graphique
et en faire une représentation graphique  .
.
2° Déterminer les réels  et
et  tels que :
tels que :
 .
.
3° Calculer l’aire du sous-ensemble du plan compris entre l'axe des abscisses du repère, la courbe  et les droites d'équations respectives :
et les droites d'équations respectives :
 et
et  .
.
Solution
 est définie sur
est définie sur  et impaire donc il suffit de l'étudier sur
et impaire donc il suffit de l'étudier sur  et
et ![{\displaystyle \left]2,+\infty \right[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c454fc5f4fae435669631b2707546a3316a9ec4c) .
.  est du signe de
est du signe de  . Quand
. Quand  croît de
croît de  à
à  ,
,  croît (strictement) de
croît (strictement) de  à
à  . Quand
. Quand  croît de
croît de  à
à  ,
,  décroît de
décroît de  à
à  .
.
Le reste de l'étude s'obtient par imparité et l'on obtient le tableau de variation suivant :

La courbe représentative (symétrique par rapport à l'origine) de la fonction  est :
est :

 .
.- On peut utiliser la question 2 :
![{\displaystyle \int _{-1}^{\frac {3}{2}}f=\left[{\frac {-1}{x-2}}+{\frac {1}{x+2}}\right]_{-1}^{\frac {3}{2}}=\dots }](https://wikimedia.org/api/rest_v1/media/math/render/svg/808a46905d21bb2250e897fd0cb2c59623e80aae) mais le calcul direct est plus rapide :
mais le calcul direct est plus rapide :
![{\displaystyle \int _{-1}^{\frac {3}{2}}{\frac {8x}{(x^{2}-4)^{2}}}\,\mathrm {d} x=4\int _{-3}^{\frac {-7}{4}}{\frac {\mathrm {d} t}{t^{2}}}=4\left[{\frac {-1}{t}}\right]_{-3}^{\frac {-7}{4}}=4\left({\frac {4}{7}}-{\frac {1}{3}}\right)={\frac {20}{21}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ce21b515eef5990e96cef7b78b4457173d6238e9) .
.
1° Construire dans un repère le graphique  de la fonction
de la fonction  définie par :
définie par :
![{\displaystyle x\in [0,\,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/68c5912bcfb6a7e7d8fc3b326024d58367f8f9fe) et
et  .
.
2° Déterminer  pour que, dans le demi-plan
pour que, dans le demi-plan  , la droite d'équation
, la droite d'équation  partage le sous-ensemble délimité par
partage le sous-ensemble délimité par  et l'axe des abscisses du repère en deux sous-ensembles d'aires égales.
et l'axe des abscisses du repère en deux sous-ensembles d'aires égales.
Soit  la fonction définie par :
la fonction définie par :
 .
.
1° Calculer  et
et  pour que
pour que  et pour que
et pour que  admette un minimum pour
admette un minimum pour  . Tracer le graphique
. Tracer le graphique  de
de  dans un repère. Déterminer son asymptote oblique
dans un repère. Déterminer son asymptote oblique  .
.
2° Calculer l’aire du sous-ensemble plan compris entre  ,
,  et les droites d'équations respectives
et les droites d'équations respectives  et
et  . Cette aire a-t-elle une limite lorsque
. Cette aire a-t-elle une limite lorsque  tend vers
tend vers  ?
?
Calculer l'aire de
![{\displaystyle D=\{(x,y)\in [0,1]\times \mathbb {R} _{+}\mid x^{2}+y^{2}\geq 1,\;y\leq 1+x^{2}\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/276be6573eb26d4298d196fbbdc1dc3f8c68f566) .
.
Calculer les aires de :
 ;
; .
.






![{\displaystyle 1+\int _{1}^{4}\left({\frac {1}{x}}+{\frac {1}{x^{2}}}\right)\,\mathrm {d} x=1+\left[\ln x-{\frac {1}{x}}\right]_{1}^{4}={\frac {7}{4}}+\ln 4}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc29f39dc9bc869bbcef1c8ea93dce08b754ae77)

![{\displaystyle \int _{-{\frac {\pi }{4}}}^{0}(\cos -\tan )=\left[\sin +\ln |\cos |\right]_{-{\frac {\pi }{4}}}^{0}={\frac {{\sqrt {2}}+\ln 2}{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/107c568c0a7d767cf690eb755031a98e54abf02f)



![{\displaystyle \left[-4,4\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2054bdf8d576d3729a4a5e6f2dd30765e74c527e)
![{\displaystyle \left[0,4\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd04af5bb35776de469be99e538a5cc93c2c90bb)
![{\displaystyle \left]0,4\right[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/042a5c9cec5e492d4d78e4efb5628ac5233bee54)





![{\displaystyle \int _{-4}^{4}f=2\left[{\frac {2(4+x)^{3/2}}{3}}-{\frac {2(4-x)^{3/2}}{3}}-2x{\sqrt {2}}\right]_{0}^{4}={\frac {16{\sqrt {2}}}{3}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b981f34886ba223036d8a1ba6893f40fd53dea7c)








![{\displaystyle \left]2,+\infty \right[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c454fc5f4fae435669631b2707546a3316a9ec4c)












![{\displaystyle \int _{-1}^{\frac {3}{2}}f=\left[{\frac {-1}{x-2}}+{\frac {1}{x+2}}\right]_{-1}^{\frac {3}{2}}=\dots }](https://wikimedia.org/api/rest_v1/media/math/render/svg/808a46905d21bb2250e897fd0cb2c59623e80aae)
![{\displaystyle \int _{-1}^{\frac {3}{2}}{\frac {8x}{(x^{2}-4)^{2}}}\,\mathrm {d} x=4\int _{-3}^{\frac {-7}{4}}{\frac {\mathrm {d} t}{t^{2}}}=4\left[{\frac {-1}{t}}\right]_{-3}^{\frac {-7}{4}}=4\left({\frac {4}{7}}-{\frac {1}{3}}\right)={\frac {20}{21}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ce21b515eef5990e96cef7b78b4457173d6238e9)
![{\displaystyle x\in [0,\,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/68c5912bcfb6a7e7d8fc3b326024d58367f8f9fe)
























![{\displaystyle D=\{(x,y)\in [0,1]\times \mathbb {R} _{+}\mid x^{2}+y^{2}\geq 1,\;y\leq 1+x^{2}\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/276be6573eb26d4298d196fbbdc1dc3f8c68f566)






![{\displaystyle \int _{-1}^{1}(4-x^{3}-x^{2})\,\mathrm {d} x=\left[4x-{\frac {x^{4}}{4}}-{\frac {x^{3}}{3}}\right]_{-1}^{1}={\frac {22}{3}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8fc5678140c76e5b70c9231444a246bbe1ceb7d2)



![{\displaystyle A_{1}=\int _{1-{\sqrt {2}}}^{1+{\sqrt {2}}}(-x^{2}+2x+1)\,\mathrm {d} x=\int _{-{\sqrt {2}}}^{\sqrt {2}}(2-t^{2})\,\mathrm {d} t=\left[2t-{\frac {t^{3}}{3}}\right]_{-{\sqrt {2}}}^{\sqrt {2}}={\frac {8{\sqrt {2}}}{3}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/35c72f70b613981db15a59c1aca44575f97fb57a)

