En raison de limitations techniques, la typographie souhaitable du titre, «
Exercice : Calculs d'aires 3
Intégration en mathématiques/Exercices/Calculs d'aires 3 », n'a pu être restituée correctement ci-dessus.
Toutes les courbes représentatives considérées sont supposées tracées dans un repère orthonormé.
Déterminer l'aire du sous-ensemble du plan délimité par les courbes représentatives des fonctions  et
et  définies par :
définies par :
 ;
; .
.
Solution
 .
.
![{\displaystyle \int _{-4}^{6}(g-f)=\left[-2\left({\frac {x}{2}}\right)^{3}+2\left({\frac {x}{2}}\right)^{2}+12x\right]_{-4}^{6}=-2(27+8)+2(9-4)+12(6+4)=60}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2bbc8d836080551e82e6c9576c5129a4d70e22e5) .
.
Déterminer l'aire du sous-ensemble du plan délimité par les courbes représentatives des fonctions  et
et  définies par :
définies par :
 ;
; .
.
Solution
![{\displaystyle \int _{-\pi }^{0}|f-g|=2\int _{-\pi /2}^{0}(f-g)=2\left[\sin x-{\frac {x^{2}}{\pi }}-x\right]_{-\pi /2}^{0}=-2\left(-1-{\frac {\pi }{4}}+{\frac {\pi }{2}}\right)=2-{\frac {\pi }{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b6c0b3dc11192f458730cf024f0cdbbd6e30f47) .
.
Déterminer l'aire du sous-ensemble du plan délimité par les courbes représentatives des fonctions  et
et  définies par :
définies par :
 ;
;![{\displaystyle g(x)={\sqrt[{4}]{x}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a3d235f1cbc0872a4586cc3dd31561994d7a17c) .
.
Solution
![{\displaystyle \int _{0}^{1}(g-f)=\left[{\frac {4x^{5/4}-x^{5}}{5}}\right]_{0}^{1}={\frac {3}{5}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee73870caf44cc2abae0482cccc1d7332b526d27) .
.
Déterminer l'aire du sous-ensemble du plan délimité par les courbes représentatives des fonctions  et
et  définies par :
définies par :
 ;
; .
.
Solution
 .
.
![{\displaystyle \int _{-1}^{2}(g-f)=\left[-{\frac {x^{3}}{3}}+{\frac {x^{2}}{2}}+2x\right]_{-1}^{2}={\frac {9}{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/760e02427f1cb061fb1e21cc67eb8379fc18a076) .
.
On considère la fonction  .
.
1° Calculer  et
et  .
.
2° En déduire l'expression générale des primitives de la fonction  .
.
3° Quelle est, parmi les fonctions données, celles dont la courbe représentative  passe par le point
passe par le point  et a une tangente au point d'abscisse
et a une tangente au point d'abscisse  parallèle à la première bissectrice ? Soit
parallèle à la première bissectrice ? Soit  cette fonction.
cette fonction.
4° Étudier la variation de  et tracer sa courbe représentative dans un repère orthonormal
et tracer sa courbe représentative dans un repère orthonormal  .
.
5° Calculer l’aire comprise entre la courbe  , l'axe des abscisses et les deux droites d'équations respectives
, l'axe des abscisses et les deux droites d'équations respectives  et
et  , et donner le résultat en centimètres carrés (unité graphique 2 cm).
, et donner le résultat en centimètres carrés (unité graphique 2 cm).
Solution
 et
et  .
.- D'après la question précédente, une primitive de
 est
est  avec
avec  définis par
définis par  et
et  , c'est-à-dire
, c'est-à-dire  et
et  . Les primitives de
. Les primitives de  sont donc les fonctions
sont donc les fonctions  , avec
, avec  .
.
 donc
donc  .
. est impaire et
est impaire et  , donc il suffit de l'étudier sur
, donc il suffit de l'étudier sur ![{\displaystyle \left[0,\pi /2\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/87cc5d5d43d0681db709db9a3fa43af6ba079a6f) . Sur cet intervalle, elle est croissante jusqu'à
. Sur cet intervalle, elle est croissante jusqu'à  puis décroissante, avec
puis décroissante, avec  .
.
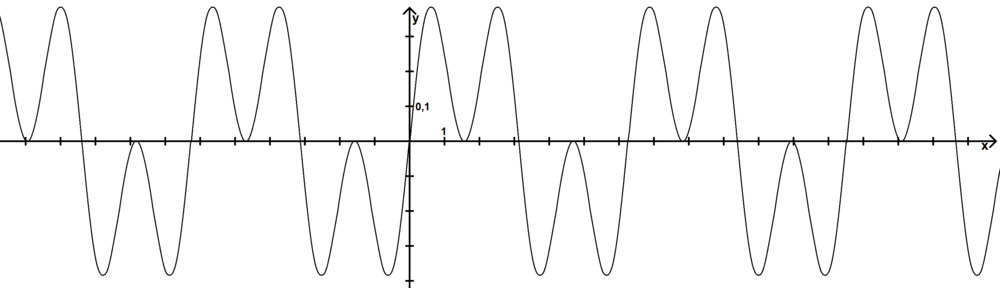
![{\displaystyle \left[-\cos ^{3}/3\right]_{0}^{\frac {\pi }{2}}=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f14ae059f0fec3ad2fb99d1ec41e2b3fd6371958) ¹⁄₃ unité d'aire, soit ⁴⁄₃ cm2.
¹⁄₃ unité d'aire, soit ⁴⁄₃ cm2.
1° Soit  la fonction définie par :
la fonction définie par :

- où
 est un nombre réel donné.
est un nombre réel donné.
- Pour quelles valeurs de
 cette fonction est-elle définie sur
cette fonction est-elle définie sur  tout entier ?
tout entier ?
- En supposant qu'il en est ainsi, étudier la variation de cette fonction.
2° Construire la courbe  représentant la fonction
représentant la fonction  .
.
- Démontrer que la courbe
 a un centre de symétrie
a un centre de symétrie  . On notera que
. On notera que  peut s'écrire sous la forme :
peut s'écrire sous la forme :
 .
.- Déterminer la tangente en
 à la courbe.
à la courbe.
3° Soit  le point de
le point de  représentant le maximum de la fonction
représentant le maximum de la fonction  .
.
- Calculer l'aire de la surface comprise entre l'arc
 de
de  et sa corde.
et sa corde.
Solution
![{\displaystyle a^{2}-4<0\Leftrightarrow a\in \left]-2,2\right[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0308e8ec5e8eb3b680ce7ea7a469e7e2883b1eba) .
.
 donc
donc  est croissante sur
est croissante sur ![{\displaystyle \left[-1,1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79566f857ac1fcd0ef0f62226298a4ed15b796ad) et décroissante sur
et décroissante sur ![{\displaystyle \left]-\infty ,-1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5be7fae2278a8ec8948f983874759124880c1018) et sur
et sur  . Sa limite en
. Sa limite en  est
est  , et
, et  ,
,  .
.- Le tableau de variation est ː

Le tracé de la courbe  est alors ː
est alors ː
La courbe  est symétrique par rapport au point
est symétrique par rapport au point  car
car  est impaire.
est impaire.
La tangente en ce point a pour équation  .
.
 a pour coordonnées
a pour coordonnées  donc
donc  a pour équation
a pour équation  .
.
![{\displaystyle \int _{0}^{1}\left(f_{0}(x)-1-x\right)\,\mathrm {d} x=\int _{0}^{1}\left({\frac {2x}{x^{2}+1}}-x\right)\,\mathrm {d} x=\left[\ln \left(x^{2}+1\right)-{\frac {x^{2}}{2}}\right]_{0}^{1}=\ln 2-{\frac {1}{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c035a36a5c70510f3401d7e2cd3c08601532f84e) .
.
1° Déterminer toutes les racines du polynôme  , en remarquant qu'il s'annule pour
, en remarquant qu'il s'annule pour  .
.
2° Étudier la fonction  définie par :
définie par :

- et en construire la courbe représentative
 dans un repère orthonormal.
dans un repère orthonormal.
3° Préciser la position de la courbe  par rapport à la parabole
par rapport à la parabole  d'équation
d'équation  .
.
4° Calculer, en fonction de  , l'aire de la région limitée par la courbe
, l'aire de la région limitée par la courbe  , la parabole
, la parabole  , la droite
, la droite  et la droite
et la droite  .
.
5° Déterminer  , à
, à  près, pour que cette aire soit égale à
près, pour que cette aire soit égale à  .
.
Solution
 .
. est définie sur
est définie sur  . Grâce à la question précédente,
. Grâce à la question précédente,  est du signe de
est du signe de  donc
donc  est décroissante sur
est décroissante sur ![{\displaystyle \left]-\infty ,0\right[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d10c3a4dbadb446d3509e7d7f25654de172d94be) et sur
et sur ![{\displaystyle \left]0,1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/091455b6e9ffc33569e2fd6f11ca6e7a4dc074f4) , puis croissante sur
, puis croissante sur  .
. 
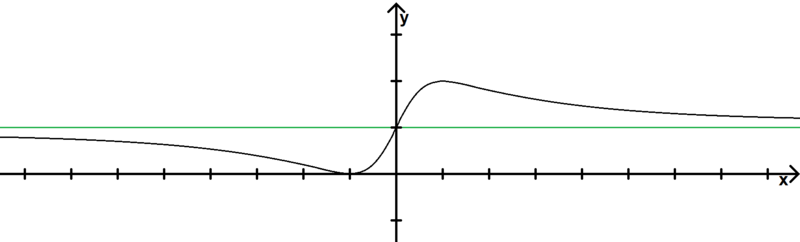
Le tableau de variation est ː

Le tracé de la courbe  (en noir sur le dessin) est alors ː
(en noir sur le dessin) est alors ː

 donc
donc  est au-dessus de
est au-dessus de  pour
pour  et en dessous pour
et en dessous pour  .
.
La parabole  a été représentée en vert sur le tracé ci-dessus et joue le rôle d'asymptote parabolique vis-à-vis de
a été représentée en vert sur le tracé ci-dessus et joue le rôle d'asymptote parabolique vis-à-vis de  .
. .
.![{\displaystyle a={\sqrt[{3}]{\mathrm {e} }}\approx 1{,}40}](https://wikimedia.org/api/rest_v1/media/math/render/svg/52cd53b99164ecd9c1d1aad6261e5c602f1aecf3) .
.
Quelle est l'aire de la surface comprise entre les courbes d'équations  et
et  pour
pour  ?
?
Solution

donc
![{\displaystyle \int _{-3}^{2}\left|x^{2}-(2-x)\right|\,\mathrm {d} x=\int _{-3}^{-2}\left(x^{2}+x-2\right)\,\mathrm {d} x-\int _{-2}^{1}\left(x^{2}+x-2\right)\,\mathrm {d} x+\int _{1}^{2}\left(x^{2}+x-2\right)\,\mathrm {d} x=\left[{\frac {x^{3}}{3}}+{\frac {x^{2}}{2}}-2x\right]_{-3}^{-2}-\left[{\frac {x^{3}}{3}}+{\frac {x^{2}}{2}}-2x\right]_{-2}^{1}+\left[{\frac {x^{3}}{3}}+{\frac {x^{2}}{2}}-2x\right]_{1}^{2}={\frac {11}{6}}+{\frac {9}{2}}+{\frac {11}{6}}={\frac {31}{6}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8f0d76bfea2281aa6ead2a05b2d7dc2812328a12) .
.











![{\displaystyle \int _{-4}^{6}(g-f)=\left[-2\left({\frac {x}{2}}\right)^{3}+2\left({\frac {x}{2}}\right)^{2}+12x\right]_{-4}^{6}=-2(27+8)+2(9-4)+12(6+4)=60}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2bbc8d836080551e82e6c9576c5129a4d70e22e5)


![{\displaystyle \int _{-\pi }^{0}|f-g|=2\int _{-\pi /2}^{0}(f-g)=2\left[\sin x-{\frac {x^{2}}{\pi }}-x\right]_{-\pi /2}^{0}=-2\left(-1-{\frac {\pi }{4}}+{\frac {\pi }{2}}\right)=2-{\frac {\pi }{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b6c0b3dc11192f458730cf024f0cdbbd6e30f47)

![{\displaystyle g(x)={\sqrt[{4}]{x}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a3d235f1cbc0872a4586cc3dd31561994d7a17c)
![{\displaystyle \int _{0}^{1}(g-f)=\left[{\frac {4x^{5/4}-x^{5}}{5}}\right]_{0}^{1}={\frac {3}{5}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee73870caf44cc2abae0482cccc1d7332b526d27)



![{\displaystyle \int _{-1}^{2}(g-f)=\left[-{\frac {x^{3}}{3}}+{\frac {x^{2}}{2}}+2x\right]_{-1}^{2}={\frac {9}{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/760e02427f1cb061fb1e21cc67eb8379fc18a076)























![{\displaystyle \left[0,\pi /2\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/87cc5d5d43d0681db709db9a3fa43af6ba079a6f)



![{\displaystyle \left[-\cos ^{3}/3\right]_{0}^{\frac {\pi }{2}}=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f14ae059f0fec3ad2fb99d1ec41e2b3fd6371958)











![{\displaystyle a^{2}-4<0\Leftrightarrow a\in \left]-2,2\right[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0308e8ec5e8eb3b680ce7ea7a469e7e2883b1eba)

![{\displaystyle \left[-1,1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79566f857ac1fcd0ef0f62226298a4ed15b796ad)
![{\displaystyle \left]-\infty ,-1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5be7fae2278a8ec8948f983874759124880c1018)













![{\displaystyle \int _{0}^{1}\left(f_{0}(x)-1-x\right)\,\mathrm {d} x=\int _{0}^{1}\left({\frac {2x}{x^{2}+1}}-x\right)\,\mathrm {d} x=\left[\ln \left(x^{2}+1\right)-{\frac {x^{2}}{2}}\right]_{0}^{1}=\ln 2-{\frac {1}{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c035a36a5c70510f3401d7e2cd3c08601532f84e)












![{\displaystyle \left]-\infty ,0\right[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d10c3a4dbadb446d3509e7d7f25654de172d94be)
![{\displaystyle \left]0,1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/091455b6e9ffc33569e2fd6f11ca6e7a4dc074f4)







![{\displaystyle a={\sqrt[{3}]{\mathrm {e} }}\approx 1{,}40}](https://wikimedia.org/api/rest_v1/media/math/render/svg/52cd53b99164ecd9c1d1aad6261e5c602f1aecf3)




![{\displaystyle \int _{-3}^{2}\left|x^{2}-(2-x)\right|\,\mathrm {d} x=\int _{-3}^{-2}\left(x^{2}+x-2\right)\,\mathrm {d} x-\int _{-2}^{1}\left(x^{2}+x-2\right)\,\mathrm {d} x+\int _{1}^{2}\left(x^{2}+x-2\right)\,\mathrm {d} x=\left[{\frac {x^{3}}{3}}+{\frac {x^{2}}{2}}-2x\right]_{-3}^{-2}-\left[{\frac {x^{3}}{3}}+{\frac {x^{2}}{2}}-2x\right]_{-2}^{1}+\left[{\frac {x^{3}}{3}}+{\frac {x^{2}}{2}}-2x\right]_{1}^{2}={\frac {11}{6}}+{\frac {9}{2}}+{\frac {11}{6}}={\frac {31}{6}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8f0d76bfea2281aa6ead2a05b2d7dc2812328a12)