Généralités sur les fonctions/Exercices/Lecture graphique d'images et d'antécédents
Exercice 4-1
[modifier | modifier le wikicode]Lecture graphique d'images
a) Lire graphiquement . Traduire par une phrase en français.
À l’abscisse de valeur 2, on voit que le point de la courbe verte se trouve sur l'ordonnée de valeur 1.
Donc .
b) Lire graphiquement . Peut-on savoir s'il s'agit d'une valeur exacte ? Justifier.
À l’abscisse de valeur 4, on voit que le point de la courbe verte se trouve sur l'ordonnée de valeur 2, le point noir se situant exactement sur le quadrillage de point de coordonnées (4;2). Donc .
c) Lire graphiquement . Peut-on savoir s'il s'agit d'une valeur exacte ? Justifier.
À l’abscisse de valeur 3, on voit que le point de la courbe verte se trouve sur l'ordonnée de valeur 1,5. Il n'y a pas de point noir situant exactement sur le quadrillage la position de la courbe ; la valeur n'est peut-être pas exacte. Donc .
d) Lire graphiquement . Peut-on savoir s'il s'agit d'une valeur exacte ? Justifier.
À l’abscisse de valeur 7,5, on voit que le point de la courbe rouge se trouve sur l'ordonnée de valeur 1, le point noir se situant exactement sur le quadrillage de point de coordonnées (7,5;1). Donc
e) Lire graphiquement et . Traduire par une phrase en français.
À l’abscisse de valeur 5, on voit que le point de la courbe rouge se trouve sur l'ordonnée de valeur 1. Il en est de même pour la courbe rouge, le point noir se situant exactement sur le quadrillage de point de coordonnées (5;1).
Donc .
f) Lire graphiquement et . Traduire par une phrase en français.
À l’abscisse de valeur 8, on voit que le point de la courbe rouge se trouve sur l'ordonnée de valeur –1. Il en est de même pour la courbe rouge, le point noir se situant exactement sur le quadrillage de point de coordonnées (8;–1).
Donc .
Exercice 4-2
[modifier | modifier le wikicode]Lecture graphique d'images
a)
- Traduire par une phrase en français.
b) Lire graphiquement , , ,, , , .
c) Présenter ces résultats (ne pas oublier celui du a)) dans un tableau de valeurs :
| x | 0 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
d)
- Traduire par une phrase en français.
e) Lire graphiquement , , , , , , .
f) Présenter ces résultats (ne pas oublier celui du d)) dans un tableau de valeurs :
| x | 0 | |||||||
|---|---|---|---|---|---|---|---|---|
Cette solution n'a pas été rédigée. Vous pouvez le faire en modifiant le paramètre « contenu » du modèle. Comment faire ?
Exercice 4-3
[modifier | modifier le wikicode]Lecture graphique d'antécédents
a) Donner par lecture graphique les antécédents de 1 par .
b) Donner par lecture graphique les antécédents de 2 par .
c) Donner par lecture graphique les antécédents de 3 par .
d) Donner par lecture graphique les antécédents de 4 par .
e) Donner par lecture graphique les antécédents de –3 par .
f) Donner par lecture graphique les antécédents de –2 par .
g) Donner par lecture graphique les antécédents de –1 par .
Cette solution n'a pas été rédigée. Vous pouvez le faire en modifiant le paramètre « contenu » du modèle. Comment faire ?
Exercice 4-4
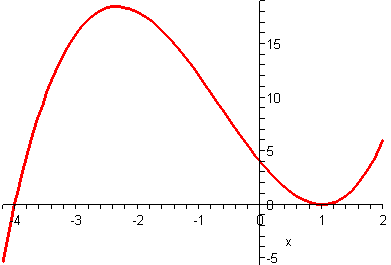
[modifier | modifier le wikicode]La courbe ci-dessous représente une fonction f définie sur [–4, 2].
a) Par lecture graphique, donner le tableau de variations de f.
b) Par lecture graphique, donner une valeur approchée au dixième de f(–2).
c) Par lecture graphique, donner une valeur approchée à l'unité des antécédents de 2 par f.
d) Soit k un réel quelconque. Discuter en fonction de k le nombre de ses antécédents par f.
Cette solution n'a pas été rédigée. Vous pouvez le faire en modifiant le paramètre « contenu » du modèle. Comment faire ?