Fonctions trigonométriques/Propriétés préliminaires

Début de la boite de navigation du chapitre

fin de la boite de navigation du chapitre

Ce chapitre est destiné à étudier des propriétés qui nous seront utiles pour calculer des limites faisant intervenir des fonctions trigonométriques. La propriété 1 de ce chapitre est souvent admise dans des cours similaires. Nous avons toutefois choisi de la déduire de lemmes qui nous semblent plus intuitifs à admettre que la propriété 1.

Considérations sur les arcs de cercle

Nous avons tout d'abord le lemme suivant :

Début d'un lemme

Lemme 1

Soit un cercle de centre $O$ sur lequel sont choisis deux points $A$ et $B$. Alors la longueur de l'arc ${\overset {\frown }{AB}}$ est supérieure à la longueur de la corde $[AB]$.

Fin du lemme

Nous admettrons ce lemme très intuitif, qui découle du fait bien connu que la ligne droite est le plus court chemin d'un point à un autre.

Nous retiendrons ensuite le lemme suivant :

Début d'un lemme

Lemme 2

Soit un cercle de centre $O$ sur lequel sont choisis deux points $A$ et $B$. Alors la longueur de l'arc ${\overset {\frown }{AB}}$ rentrant est inférieure à la longueur de tout chemin extérieur au cercle reliant les points $A$ et $B$.

Fin du lemme

Nous admettrons aussi ce lemme, difficile à démontrer bien qu'assez intuitif.

Continuité de la fonction sinus

Rappel

Nous rappelons qu'une fonction $f$ est continue en une valeur $a$ de son domaine de définition si :

$\lim _{x\to a}f(x)=f(a)$,

ce qui est équivalent à :

$\lim _{h\to 0}f(a+h)=f(a)$.

Nous montrerons la continuité de la fonction sinus grâce au lemme suivant :

Début d'un lemme

Lemme 3

$|\sin x|<|x|$.

Fin du lemme

Preuve du lemme 3 grâce au lemme 1

Considérons un arc ${\overset {\frown }{AM}}$ du cercle trigonométrique dont la mesure en radians est $x$ avec :

$|x|<{\frac {\pi }{2}}$

et soit $N$, le symétrique de $M$ par rapport à l'axe des abscisses.

Si $x$ est négatif, on visualisera que les points $M$ et $N$ sont inversés sur la figure.

Dans les deux cas de figure nous voyons que la longueur de l'arc ${\overset {\frown }{AM}}$ est $|x|$ et la longueur du segment $[BM]$ est $|\sin x|$.

D'après le lemme 1, la longueur de la corde $[NM]$ est inférieure à la longueur de l'arc ${\overset {\frown }{NM}}$, ce qui nous donne, par symétrie :

$2|\sin x|<2|x|$

soit, en simplifiant :

$|\sin x|<|x|$.

 

Preuve du lemme 3 par les aires

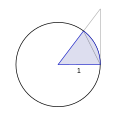
Considérons le cercle unité sur la figure suivante, où l'angle $\theta$ est compris entre $0$ et ${\frac {\pi }{2}}$, et comparons deux aires présentes dans cette figure :

• 
• 
• 

Le triangle rouge est contenu dans le secteur circulaire bleu donc :

${\frac {\sin \theta }{2}}<{\frac {\theta }{2}}$,

ou encore (en multipliant les deux membres par le nombre ${\frac {2}{\theta }}>0$) :

${\frac {\sin \theta }{\theta }}<1$.

 

Montrons que la fonction sinus est continue en une valeur $a$ quelconque de son domaine de définition qui est $\mathbb {R}$.

De l'une des formules de Simpson :

$\sin p-\sin q=2\sin {\frac {p-q}{2}}\cos {\frac {p+q}{2}}$,

on déduit, grâce au lemme 3 :

$|\sin x-\sin a|=2\left|\sin {\frac {x-a}{2}}\right|\left|\cos {\frac {x+a}{2}}\right|\leq 2\times \left|{\frac {x-a}{2}}\right|\times 1=|x-a|$,

d'où il découle, d'après le théorème de l'encadrement (théorème des gendarmes) :

$\lim _{x\to a}|\sin x-\sin a|=0$,

autrement dit :

$\lim _{x\to a}\sin x=\sin a$,

ce qui montre que la fonction sinus est bien continue en $a$.

Continuité de la fonction cosinus

Nous invitons le lecteur, à titre d'entraînement, à faire une démonstration similaire à celle de la fonction sinus en utilisant une autre formule de Simpson :

$\cos p-\cos q=-2\sin {\frac {p-q}{2}}\sin {\frac {p+q}{2}}$.

Quant à nous, nous nous contenterons de remarquer que :

$\cos x=\sin \left(x+{\frac {\pi }{2}}\right)$,

qui nous montre que la continuité de la fonction cosinus découle directement, par composition de fonctions continues, de la continuité de la fonction sinus.

Continuité de la fonction tangente

Comme :

$\tan x={\frac {\sin x}{\cos x}}$,

la fonction tangente est continue comme quotient de deux fonctions continues.

Propriétés sur les limites

La propriété 1 ci-dessous est assez fondamentale et permet d'établir un grand nombre de limites d'expressions contenant des fonctions trigonométriques. Nous verrons en particulier que grâce à celle-ci, nous pourrons calculer la dérivée des fonctions sinus et cosinus.

Propriété 1

$\lim _{x\to 0}{\frac {\sin x}{x}}=1$.

Pour démontrer cette propriété, nous utiliserons le lemme 3 et le lemme suivant :

Début d'un lemme

Lemme 4

Pour tout réel $x\neq 0$ tel que $|x|\leq {\frac {\pi }{2}}$, on a :

$\cos x<{\frac {\sin x}{x}}$.

Fin du lemme

Preuve du lemme 4 grâce au lemme 2

Nous supposons que $x$ est positif et invitons le lecteur à refaire l'étude en supposant $x$ négatif.

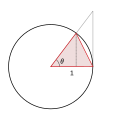
Reprenons la figure de la première preuve du lemme 3 — nous avions entre autres ${\overset {\frown }{NM}}=2x$ — et ajoutons-y la tangente en $M$ au cercle trigonométrique et $T$, son point d'intersection avec l’axe des abscisses. Comme $[OM]$ est un rayon du cercle trigonométrique, on a $OM=1$ et donc :

$TM=\tan x$.

Par symétrie, on a également $NT=\tan x$.

La réunion des segments $[NT]$ et $[TM]$ constitue un chemin extérieur au cercle trigonométrique reliant les points $N$ et $M$. Par conséquent, la longueur de ce chemin est, d'après le lemme 2, supérieure à celle de l'arc ${\overset {\frown }{NM}}$. On a donc :

$2x<2\tan x$,

soit :

$x<\tan x={\frac {\sin x}{\cos x}}$

et nous obtenons :

$\cos x<{\frac {\sin x}{x}}$.

 

Preuve du lemme 4 par les aires

Reprenons la figure de la seconde preuve du lemme 3 et comparons maintenant les deux aires suivantes :

• 
• 

Le secteur circulaire bleu est contenu dans le triangle vert donc :

${\frac {\theta }{2}}<{\frac {\tan \theta }{2}}$,

ou encore (en multipliant les deux membres par le nombre ${\frac {2\cos \theta }{\theta }}>0$) :

$\cos \theta <{\frac {\sin \theta }{\theta }}$.

 

Les lemmes 3 et 4 nous donnent deux inégalités qui peuvent se réunir en un encadrement :

$\cos x<{\frac {\sin x}{x}}<1$.

La fonction cosinus étant continue en $0$, nous avons :

$\lim _{x\to 0}\cos x=\cos 0=1$.

Par conséquent, en faisant tendre $x$ vers $0$ dans les trois membres de $\cos x<{\frac {\sin x}{x}}<1$, nous obtenons en utilisant le théorème de l'encadrement (théorème des gendarmes) :

$\lim _{x\to 0}{\frac {\sin x}{x}}=1$.

La propriété suivante se déduit de la propriété 1 mais est aussi importante pour faciliter l'établissement de limites d'expressions contenant des fonctions trigonométriques.

Propriété 2

$\lim _{x\to 0}{\frac {1-\cos x}{x^{2}}}={\frac {1}{2}}$.

Démonstration

Nous partirons de la formule de duplication :

$\cos 2a=1-2\sin ^{2}a$.

En posant $a={\frac {x}{2}}$, nous obtenons :

$\cos x=1-2\sin ^{2}{\frac {x}{2}}$,

et donc :

${\frac {1-\cos x}{x^{2}}}={\frac {2\sin ^{2}{\frac {x}{2}}}{x^{2}}}={\frac {1}{2}}\left({\frac {\sin {\frac {x}{2}}}{\frac {x}{2}}}\right)^{2}$.

Posons $X={\frac {x}{2}}$.

${\frac {1-\cos x}{x^{2}}}={\frac {1}{2}}\left({\frac {\sin X}{X}}\right)^{2}$.

Si l’on fait tendre $x$ vers $0$, alors $X$ tend aussi vers $0$. Par conséquent, en utilisant la propriété 1, on a :

$\lim _{x\to 0}{\frac {1-\cos x}{x^{2}}}=\lim _{X\to 0}{\frac {1}{2}}\left({\frac {\sin X}{X}}\right)^{2}={\frac {1}{2}}\times 1^{2}={\frac {1}{2}}$.