Fonctions trigonométriques/Étude de la fonction sinus

Début de la boite de navigation du chapitre

fin de la boite de navigation du chapitre

Dans ce chapitre, nous allons étudier la fonction sinus en détail de façon à pouvoir préciser son tracé. Le point important de ce chapitre est l'établissement de la dérivée de la fonction sinus dont il conviendra de bien retenir le résultat.

Établissement du domaine d'étude

Les chapitres précédents nous ont déjà appris que la fonction sinus est définie sur $\mathbb {R}$ et qu'elle est continue.

Nous rappelons qu'une fonction $f$ est périodique et de période $T$ si :

$\forall x\in \mathbb {R} \qquad f(x+T)=f(x)$.

Or nous savons que :

$\sin(x+2\pi )=\sin x$.

Nous en déduisons, de façon immédiate, que la fonction sinus est périodique de période $2\pi$.

Nous pouvons donc étudier la fonction sinus sur un intervalle de largeur $2\pi$.

Nous pouvons, par exemple, prendre l'intervalle $[0,2\pi ]$.

Mais ce choix n'est pas très astucieux, pourquoi ?

Tout simplement parce la fonction sinus vérifie la relation :

$\sin(-x)=-\sin x$,

qui nous montre que la fonction sinus est impaire, c'est-à-dire que sa courbe admet l'origine du repère comme centre de symétrie.

Par conséquent, au lieu de choisir l'intervalle $[0,2\pi ]$, nous choisirons plutôt l'intervalle $[-\pi ,\pi ]$, que nous couperons ensuite en deux pour exploiter l'imparité de la fonction sinus.

Il nous restera donc, comme intervalle d'étude, seulement l'intervalle $[0,\pi ]$.

En considérant d'autres symétries, on pourrait aller plus loin dans la découpe de l'intervalle d'étude, mais nous en resterons là pour le moment (nous étudierons cela dans un chapitre ultérieur).

En résumé, nous commencerons par étudier le tracé de la fonction sinus dans l'intervalle $[0,\pi ]$. En considérant la symétrie par rapport à l'origine, nous en déduirons le tracé dans l'intervalle $[-\pi ,\pi ]$. En considérant ensuite la périodicité, nous en déduirons la totalité du tracé sur $\mathbb {R}$.

Dérivée de la fonction sinus

Rappelons que le sens de variation d'une fonction est obtenu simplement par l'étude du signe de sa dérivée : la fonction est croissante si sa dérivée est positive et décroissante si sa dérivée est négative.

Début d’un théorème

Dérivée de la fonction sinus

La fonction $\sin$ est dérivable sur $\mathbb {R}$ et sa dérivée est :

$\sin '=\cos$.

Fin du théorème

Démonstration

La définition générale de la dérivée $f'$ d'une fonction $f$ est :

$f'(x)=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}$.

Appliquons-la à $f=\sin$. Compte tenu de la formule de Simpson :

$\sin p-\sin q=2\sin {\frac {p-q}{2}}\cos {\frac {p+q}{2}}$,

en posant $p=x+h$ et $q=x$, nous obtenons :

$\sin '(x)=\lim _{h\to 0}{\frac {2\sin \left({\frac {h}{2}}\right)\cos \left(x+{\frac {h}{2}}\right)}{h}}=\lim _{h\to 0}{\frac {\sin \left({\frac {h}{2}}\right)}{\frac {h}{2}}}\lim _{h\to 0}\cos \left(x+{\frac {h}{2}}\right)$

donc (d'après la propriété 1 du chapitre précédent)

$\sin 'x=1\times \cos x$.

 

Sens de variation de la fonction sinus

Au paragraphe précédent, nous avons calculé la dérivée de la fonction sinus : $\sin '=\cos$.

Nous pouvons donc connaître le sens de variation de la fonction sinus en étudiant le signe de la fonction cosinus. Nous savons que la fonction cosinus est donnée par l'abscisse du point $M$, se trouvant sur le cercle trigonométrique, dont l'abscisse curviligne est $x$.

Nous remarquons que :

• lorsque $x$ est compris entre $0$ et ${\frac {\pi }{2}}$, l'abscisse $\cos x$ du point $M$ est positive, ce qui prouve que la fonction sinus est croissante sur $\left[0,{\frac {\pi }{2}}\right]$ ;
• lorsque $x$ est compris entre ${\frac {\pi }{2}}$ et $\pi$, l'abscisse $\cos x$ du point $M$ est négative, ce qui prouve que la fonction sinus est décroissante sur $\left[{\frac {\pi }{2}},\pi \right]$.

Nous pouvons résumer cela dans le tableau de variations :

${\begin{array}{c|ccccc|}x&0&&{\frac {\pi }{2}}&&\pi \\\hline \sin 'x&&+&0&-&\\\hline &&&1&&\\\sin x&&\nearrow &&\searrow &\\&0&&&&0\\\hline \end{array}}$

Compte tenu de la symétrie par rapport à l'origine et de la périodicité, nous en déduisons la courbe représentative de la fonction sinus que l'on peut représenter ainsi :

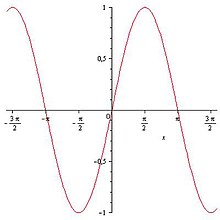
le tracé se prolongeant indéfiniment sur $\mathbb {R}$.