Discussion:Produit scalaire dans le plan

Une page de Wikiversité.

Bonjour, J'ai une question à propos d une démonstration qui concerne les produit scalaire. Si (V1•X)=p V1 et X étant des vecteurs et p un scalaire que vaut X Merci — Le message qui précède, non signé?, a été déposé par 78.29.199.246 (d · c · b).

Bonjour,
ProdScal1.png
Ce type de problème n'a pas de solution unique : il existe une infinité de vecteurs X vérifiant cette équation.
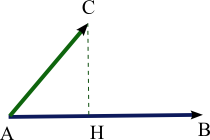
Prenons l'exemple de la figure ci-contre, où \vec v_1=\overrightarrow{\rm AB} serait le vecteur bleu et \vec x un vecteur ici tracé en vert qui vérifie la condition \vec v_1\cdot\vec x=p. Le produit scalaire est avant tout un outil de projection : on montre que, dans le cas de la figure ci-contre, \vec v_1\cdot \vec x={\rm AB}\times{\rm AH}, donc en fait n'importe quel vecteur \vec x partant de A dont l'extrémité se projetterait orthogonalement sur (AB) au point H vérifiera cette égalité.
L'ensemble des vecteurs \vec x vérifiant cette condition est alors tous les vecteurs allant du point A à un point de la perpendiculaire à (AB) passant par H. Xzapro4 discuter 3 novembre 2009 à 16:22 (UTC)
Merci beaucoup vous m avez bien aidé! — Le message qui précède, non signé?, a été déposé par Arnaud1988 (d · c · b).
Récupérée de « http://fr.wikiversity.org/wiki/Discussion:Produit_scalaire_dans_le_plan »