Équation du troisième degré/Fonctions polynômes du troisième degré

Début de la boite de navigation du chapitre

fin de la boite de navigation du chapitre

Dans ce chapitre, nous étudierons les courbes du troisième degré. Nous verrons que l'allure générale du tracé d'une courbe du troisième degré dépend principalement de deux éléments. Le premier élément est le signe du coefficient du terme de plus haut degré. Le deuxième élément est le discriminant du second degré de la dérivée de la fonction à étudier. Le discriminant du troisième degré de la fonction n'intervient, quant à lui, seulement pour préciser le nombre de points d'intersection entre la courbe et l'axe des abscisses.

Définition des éléments nécessaires à l'étude des fonctions polynômes du troisième degré

Définition

Une fonction polynomiale du troisième degré est une fonction qui peut s'exprimer sous la forme :

$f:x\mapsto ax^{3}+bx^{2}+cx+d$

avec

• a, b, c et d quatre coefficients réels
• a non nul.

On parle de troisième degré car la puissance de x la plus élevée est 3.

Pour l'étude générale des fonctions polynomiales du troisième degré, il est très important de prendre a non nul, sinon on n'aurait plus une fonction du troisième, mais du second degré maximum.

De la définition précédente, on déduit qu'une fonction polynôme du troisième degré est définie sur $\mathbb {R}$ tout entier.

Propriété

La dérivée de la fonction définie précédemment est donnée par :

$f':x\mapsto 3ax^{2}+2bx+c~$

Démonstration

Démonstration immédiate. Si vous n'y arrivez pas, ne vous découragez pas et revoyez votre cours sur les calculs de dérivées.

 

Propriété

Soit Δ est le discriminant de l'équation à résoudre et Δ' le discriminant de la dérivée de la fonction à résoudre alors, nous avons :

$\Delta =b^{2}c^{2}+18abcd-27a^{2}d^{2}-4ac^{3}-4b^{3}d~$

$\Delta '=4(b^{2}-3ac)~$

Démonstration

Pour le calcul de Δ, voir le cinquième paragraphe du chapitre précédent et éventuellement l'exercice 2-2.

Pour le calcul de Δ', on sait (revoir éventuellement le cours sur les équations du second degré) que l'équation :

$AX^{2}+BX+C=0~$

a pour discriminant :

$B^{2}-4AC~$

En posant :

$\left\{{\begin{matrix}A=3a\\B=2b\\C=c\end{matrix}}\right.$

On obtient :

$\Delta '=(2b)^{2}-4\times 3aC=4b^{2}-12ac=4(b^{2}-3ac)~$

 

Notations Par commodité, nous poserons : $\delta '=b^{2}-3ac~$ δ' est le discriminant réduit de la dérivée de la fonction à résoudre. Il a, bien sûr, le même signe que Δ' et nous dispense du facteur 4. $\Delta '=4\delta '~$ Nous poserons aussi : $\Psi =2b^{3}+27a^{2}d-9abc~$ Cette expression revient assez souvent dans l'étude des équations du troisième degré.

Le tableau de variation de la fonction du troisième degré à étudier dépend uniquement du signe du terme de plus haut degré et de Δ'. Dans la suite de ce chapitre, nous distinguerons donc quatre cas selon le signe du coefficient du terme de plus haut degré et selon le signe de Δ'. Pour chacun des quatre cas, nous tracerons les différentes courbes possibles associées au tableau de variation établi pour le cas considéré.

Premier cas : le coefficient du terme de plus haut degré est positif et Δ' est strictement positif

Début d’un théorème

Théorème

Les variations de la fonction du troisième degré :

$f(x)=ax^{3}+bx^{2}+cx+d~$

définie sur $\mathbb {R}$, avec a positif et Δ' positif, sont données par le tableau suivant :

${\begin{array}{c|ccccccc}x&-\infty &&\alpha &&\beta &&+\infty \\&&&&&&&\\\hline &&&M&&&&+\infty \\{\textrm {Variations~de}}~f&&\nearrow &&\searrow &&\nearrow &\\&-\infty &&&&m&&\\\end{array}}$

Avec :

$\alpha ={\frac {-b-{\sqrt {\delta '}}}{3a}}~$

$\beta ={\frac {-b+{\sqrt {\delta '}}}{3a}}~$

$m={\frac {\Psi -2\delta '^{\frac {3}{2}}}{27a^{2}}}~$

$M={\frac {\Psi +2\delta '^{\frac {3}{2}}}{27a^{2}}}~$

Fin du théorème

Démonstration

Étudions donc la fonction :

$f(x)=ax^{3}+bx^{2}+cx+d~$

sa dérivée est :

$f'(x)=3ax^{2}+2bx+c~$

Pour trouver les valeurs annulant la dérivée, nous devons résoudre l'équation :

$3ax^{2}+2bx+c=0~$

Cette équation a par hypothèse un discriminant strictement positif. L'équation admet donc deux racines réelles distinctes.

Le calcul des racines α et β nous donne :

$\alpha ={\frac {-b-{\sqrt {\delta '}}}{3a}}~$

$\beta ={\frac {-b+{\sqrt {\delta '}}}{3a}}~$

Comme le coefficient 3a de degré deux est positif (car a est positif par hypothèse), la dérivée est donc positive en dehors des racines et négative à l'intérieur des racines.

La fonction f est donc croissante de moins l'infini à α, décroissante de α à β et à nouveau croissante de β à plus l'infini. La fonction admet donc un maximum relatif M en α et un minimum relatif m en β. Il ne nous reste plus qu’à calculer M et m. On obtient ainsi :

$m=f(\beta )={\frac {\Psi -2\delta '^{\frac {3}{2}}}{27a^{2}}}~$

$M=f(\alpha )={\frac {\Psi +2\delta '^{\frac {3}{2}}}{27a^{2}}}~$

 

En posant :

$\Psi =2b^{3}+27a^{2}d-9abc~$

Les coordonnées du centre de symétrie sont (voir exercice 3-6) :

$\left(-{\frac {b}{3a}};{\frac {\Psi }{27a^{2}}}\right)~$

Nous voyons alors que le signe de Ψ nous renseigne sur la position du centre de symétrie par rapport à l'axe des abscisses.

Dans le tableau suivant, nous avons représenté quelques tracés de courbes qui tiennent compte du discriminant et de la position du centre de symétrie par rapport à l'axe des abscisses. Nous avons vu dans le chapitre précédent que le signe du discriminant permet de prévoir le nombre de racines réelles et par conséquent le nombre de points d'interception de la courbe avec l'axe des abscisses. La position du centre de symétrie donnée par le signe de Ψ, quant à elle, nous permet une localisation grossière des racines dans l’ensemble des nombres réels.

Les 6 cas qui peuvent se présenter

a > 0	Δ < 0	Δ > 0	Δ = 0
Ψ > 0	Une racine < -b/3a	Une racine < -b/3a < deux racines	Une racine simple < -b/3a < une racine double
Ψ < 0	Une racine > -b/3a	Deux racines < -b/3a <une racine	Une racine double < -b/3a < une racine simple

Deuxième cas : le coefficient du terme de plus haut degré est positif et Δ' est négatif ou nul

Début d’un théorème

Théorème

Les variations de la fonction du troisième degré :

$f(x)=ax^{3}+bx^{2}+cx+d~$

définie sur $\mathbb {R}$, avec a positif et Δ' négatif, sont données par le tableau suivant :

${\begin{array}{c|cccc}x&-\infty &&+\infty \\&&&\\\hline &&&+\infty \\{\textrm {Variations~de}}~f&&\nearrow &&\\&-\infty &&\\\end{array}}$

Fin du théorème

Démonstration

Étudions donc la fonction :

$f(x)=ax^{3}+bx^{2}+cx+d~$

sa dérivée est :

$f'(x)=3ax^{2}+2bx+c~$

Pour trouver les valeurs annulant la dérivée, nous devons résoudre l'équation :

$3ax^{2}+2bx+c=0~$

Cette équation a par hypothèse un discriminant strictement négatif. L'équation n'admet donc pas de racines réelles.

Comme le coefficient 3a de degré deux est positif (car a est positif par hypothèse), la dérivée est donc positive pour tout x.

La fonction f est donc croissante de moins l'infini à plus l'infini.

 

Les 4 cas qui peuvent se présenter

a > 0	Δ < 0	Δ = 0
Ψ > 0	Une racine < -b/3a	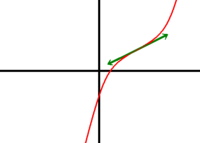Impossible
Ψ = 0	Une racine = -b/3a	Une racine triple
Ψ < 0	Une racine > -b/3a	Impossible

Troisième cas : le coefficient du terme de plus haut degré est négatif et Δ' est strictement positif

Début d’un théorème

Théorème

Les variations de la fonction du troisième degré :

$f(x)=ax^{3}+bx^{2}+cx+d~$

définie sur $\mathbb {R}$, avec a négatif et Δ' positif, sont données par le tableau suivant :

${\begin{array}{c|ccccccc}x&-\infty &&\alpha &&\beta &&+\infty \\&&&&&&&\\\hline &+\infty &&&&M&&\\{\textrm {Variations~de}}~f&&\searrow &&\nearrow &&\searrow &\\&&&m&&&&-\infty \\\end{array}}$

Avec :

$\alpha ={\frac {-b+{\sqrt {\delta '}}}{3a}}~$

$\beta ={\frac {-b-{\sqrt {\delta '}}}{3a}}~$

$m={\frac {\Psi -2\delta '^{\frac {3}{2}}}{27a^{2}}}~$

$M={\frac {\Psi +2\delta '^{\frac {3}{2}}}{27a^{2}}}~$

Fin du théorème

Démonstration

Étudions donc la fonction :

$f(x)=ax^{3}+bx^{2}+cx+d~$

sa dérivée est :

$f'(x)=3ax^{2}+2bx+c~$

Pour trouver les valeurs annulant la dérivée, nous devons résoudre l'équation :

$3ax^{2}+2bx+c=0~$

Cette équation a par hypothèse un discriminant strictement positif. L'équation admet donc deux racines réelles distinctes.

Le calcul des racines α et β nous donne :

$\alpha ={\frac {-b-{\sqrt {\delta '}}}{3a}}~$

$\beta ={\frac {-b+{\sqrt {\delta '}}}{3a}}~$

Comme le coefficient 3a de degré deux est négatif (car a est négatif par hypothèse), la dérivée est donc négative en dehors des racines et positive à l'intérieur des racines.

La fonction f est donc décroissante de moins l'infini à α, croissante de α à β et à nouveau décroissante de β à plus l'infini. La fonction admet donc un minimum relatif m en α et un maximum relatif M en β. Il ne nous reste plus qu’à calculer m et M. On obtient :

$m=f(\alpha )={\frac {\Psi -2\delta '^{\frac {3}{2}}}{27a^{2}}}~$

$M=f(\beta )={\frac {\Psi +2\delta '^{\frac {3}{2}}}{27a^{2}}}~$

 

Les 6 cas qui peuvent se présenter

a < 0	Δ < 0	Δ > 0	Δ = 0
Ψ > 0	Une racine > -b/3a	Deux racines < -b/3a < une racine	Une racine double < -b/3a < une racine simple
Ψ < 0	Une racine < -b/3a	Une racine < -b/3a < deux racines	Une racine simple < -b/3a < une racine double

Quatrième cas : le coefficient du terme de plus haut degré est négatif et Δ' est négatif ou nul

Début d’un théorème

Théorème

Les variations de la fonction du troisième degré :

$f(x)=ax^{3}+bx^{2}+cx+d~$

définie sur $\mathbb {R}$, avec a négatif et Δ' négatif, sont données par le tableau suivant :

${\begin{array}{c|cccc}x&-\infty &&+\infty \\&&&\\\hline &+\infty &&\\{\textrm {Variations~de}}~f&&\searrow &&\\&&&-\infty \\\end{array}}$

Fin du théorème

Démonstration

Étudions donc la fonction :

$f(x)=ax^{3}+bx^{2}+cx+d~$

sa dérivée est :

$f'(x)=3ax^{2}+2bx+c~$

Pour trouver les valeurs annulant la dérivée, nous devons résoudre l'équation :

$3ax^{2}+2bx+c=0~$

Cette équation a par hypothèse un discriminant strictement négatif. L'équation n'admet donc pas de racines réelles.

Comme le coefficient 3a de degré deux est négatif (car a est négatif par hypothèse), la dérivée est donc négative pour tout x.

La fonction f est donc décroissante de moins l'infini à plus l'infini.

 

Les 4 cas qui peuvent se présenter

a < 0	Δ < 0	Δ = 0
Ψ > 0	Une racine > -b/3a	Impossible
Ψ = 0	Une racine = -b/3a	Une racine triple
Ψ < 0	Une racine < -b/3a	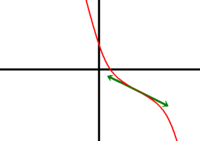Impossible