Systèmes et représentations/Fonctions d'entrée courantes
Fonctions causales[modifier | modifier le wikicode]
On appelle fonction causale une fonction f de la variable réelle t définie sur et supposée nulle pour .
- Fonction normale :
- Fonction causale :
- est définie
![{\displaystyle \forall t\in \left]-\infty ;0\right],\;f(t)=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aacdb643c7b3ca3daf5f0a1be6c55117f33699d3)
![{\displaystyle \forall t\in \left]0;+\infty \right[,\;f(t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0fdb5cac850a2d9c5fa23508a5244604251322cc)
À noter que dans toute la suite, on ne considérera que des fonctions d'entrée causales.
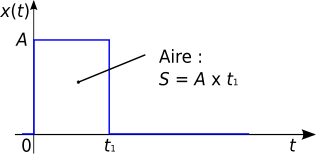
Fonctions impulsions[modifier | modifier le wikicode]
Impulsion physique (créneau)[modifier | modifier le wikicode]
Il est défini par :
![{\displaystyle \forall t\in \left]-\infty ;0\right]\bigcup \left[t_{1};+\infty \right],\quad x(t)=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e5ebd3059906f5b8c8aa740809a00cba2568e4a2)
![{\displaystyle \forall t\in \left]0;t_{1}\right[,\quad x(t)=A}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6690019c63beb5172a19b5453fd7a7d6956feb25)
Impulsion de Dirac[modifier | modifier le wikicode]
On définit une impulsion comme un créneau de surface unité (A = 1/).
L'impulsion de Dirac s'obtient en faisant tendre vers 0. Cela revient à générer un signal d'amplitude infinie pendant un temps nul.
Un tel signal ne correspond à aucun signal physique réel, mais il permet de définir ultérieurement des caractéristiques temporelles importantes d'un système dynamique. Il modélise par exemple les chocs que peut recevoir un système.
On représente une impulsion de Dirac avec une flèche :
Échelon unité (fonction existence)[modifier | modifier le wikicode]
Cette fonction est définie par :
![{\displaystyle \forall t\in \left]-\infty ;0\right],\quad x(t)=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1ec45a111161e948a993bbc6881ff94a1381124e)
![{\displaystyle \forall t\in \left]0;+\infty \right[,\quad x(t)=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f1296008884085ecf1d419d3d1d429d92fed4100)
Fonction rampe[modifier | modifier le wikicode]
Cette fonction est définie par :
![{\displaystyle \forall t\in \left]0;+\infty \right[,\quad x(t)=a\times t}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd5407b6e19b697c3290f99d24a224ccd7ec9718)
.png)
Fonction sinusoïdale[modifier | modifier le wikicode]
Cette fonction est définie par :
![{\displaystyle \forall t\in \left]0;+\infty \right[,\quad x(t)=\sin \left(\omega \,t\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/60849eff9449f5f3a550e0397f4a1668bc2ded9a)
avec ω la pulsation (en rad/s).
