Systèmes et représentations/Linéarité, principe de superposition, invariance

Début de la boite de navigation du chapitre

fin de la boite de navigation du chapitre

Un système linéaire est un système pour lequel les relations entre les grandeurs d'entrée et les grandeurs de sortie peuvent se mettre sous la forme d'un ensemble d'équations différentielles linéaires à coefficients constants.

Linéarité

Un système est dit linéaire si et seulement si : si $e(t)\Longrightarrow s(t)$ alors $a\times e(t)\Longrightarrow a\times s(t)$

Additivité (principe de superposition)

On suppose que pour une entrée e1(t), on obtient une sortie s1(t) et pour une entrée e2(t), on obtient une sortie s2(t). Alors, le principe de superposition indique :

$\forall (a,b)\in \mathbb {R} ^{2},\;\forall t,\;a\times e_{1}(t)+b\times e_{2}(t)=a\times s_{1}(t)+b\times s_{2}(t)$

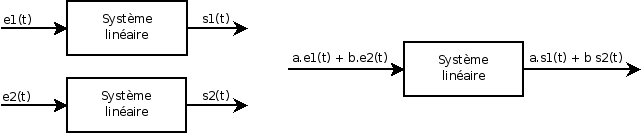
Invariance

Un système invariant est un système dont les caractéristiques de comportement ne se modifient pas dans le temps. On dit que "le système ne vieillit pas".

Ainsi, si $e(t)\Longrightarrow s(t)$, alors pour un décalage temporel $\tau >0$, on : $e(t-\tau )\Longrightarrow s(t-\tau )$.