Recherche:Décomposition en poids × niveau + saut
Attention : le titre d’affichage « Recherche:Décomposition en poids × niveau + saut » écrase l’ancien titre d’affichage « Décomposition en poids × niveau + saut ».
- arXiv:0711.0865 [math.NT]: Decomposition into weight * level + jump and application to a new classification of primes, 2007 - 2010, Rémi Eismann.
Principes
[modifier | modifier le wikicode]Principe de décomposition : on choisit le plus petit poids tel que dans la division euclidienne d'un nombre par son poids, le reste est le saut (première différence, écart). Le quotient sera le niveau.
Principes de classification: si le nombre n'est pas décomposable, il n'est pas classé. Si le poids est plus grand que le niveau alors le nombre est classé par niveau, sinon il est classé par poids.
Définitions
[modifier | modifier le wikicode]Soit , une suite strictement croissante d'entiers positifs.
Saut
[modifier | modifier le wikicode]Le saut (première différence, écart) de est défini par
l(n)
[modifier | modifier le wikicode]l(n) est défini par
Définition alternative avec la fonction mod
[modifier | modifier le wikicode]Poids
[modifier | modifier le wikicode]Le poids de est défini par
Définition alternative avec la fonction mod
[modifier | modifier le wikicode]Niveau
[modifier | modifier le wikicode]Le niveau de est défini par
Critère de décomposition
[modifier | modifier le wikicode]Un nombre d'une suite strictement croissante d'entiers positifs, peut être décomposé en poids × niveau + saut quand est différent de 0 ce qui peut être réécrit en :
ou
ou
Une décomposition unique
[modifier | modifier le wikicode]Le poids est le plus petit tel que dans la division euclidienne de par son poids , le quotient est le niveau , et le reste est le saut . Nous avons donc la décomposition unique
Principes de classification
[modifier | modifier le wikicode]- Si pour ,
alors n'est pas classé.
- Si pour ,
alors est classé par niveau, sinon il est classé par poids.
Algorithmes
[modifier | modifier le wikicode]Algorithme naïf (PARI/GP):
decompnaive(n,n1)={
/*strictly increasing*/
if(n>=n1,print("n1 must be greater than n");return);
/*jump*/
d=n1-n;
/*l=n-d if n>2*d else the number is not decomposable*/
if(n>2*d,l=n-d,print(d, ", 0, 0");return);
/*we look for the weight to jump+1 until l*/
for(k=d+1,l,if(n%k==d,print(n," = ",k," * ",l/k," + ",d);return));
}
Algorithme "newSieve":
decompsieve(n,n1)={
/*strictly increasing*/
if(n>=n1,print("n1 must be greater than n");return);
/*jump*/
d=n1-n;
/*l=n-d if n>2*d else the number is not decomposable*/
if(n>2*d,l=n-d,print(d, ", 0, 0");return);
/*we look for the weight to jump+1 until sqrt(l)*/
for(k=d+1,sqrt(l),if(n%k==d,print(n," = ",k," * ",l/k," + ",d);return));
/*we look for the level to jump until 1 (--)*/
forstep(le=d,1,-1,if(n%floor(l/le)==d,print(n," = ",l/le," * ",le," + ",d);return));
}
L'algorithmes "newSieve" est le plus rapide pour les nombres classés par niveaux.
Remarques générales
[modifier | modifier le wikicode]La suite avec la plus grande croissance qui peut être décomposée est A003312.
A travers cette page, le saut est la première différence mais on peut prendre la seconde, la troisième... Voir A133346 et A133347 pour les nombres premiers.
Décomposition des entiers naturel et le théorème fondamental de l'arithmétique
[modifier | modifier le wikicode]Si la décomposition est possible (si ), on a :
Le poids est le plus petit facteur premier de et le niveau est le plus grand diviseur propre de . Les entiers naturel classé par poids sont les composés + 1 et les entiers naturels classés par niveau sont les premiers +1. Comme le saut est constant la décomposition des entiers naturels peut se résumer à la décomposition de en poids × niveau. Et en décomposant successivement les niveaux on retombe sur la décomposition unique en facteurs premiers du théorème fondamental de l'arithmétique.
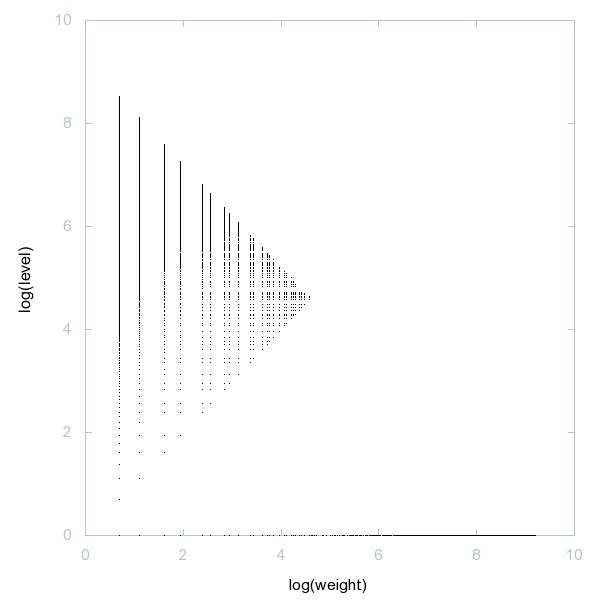
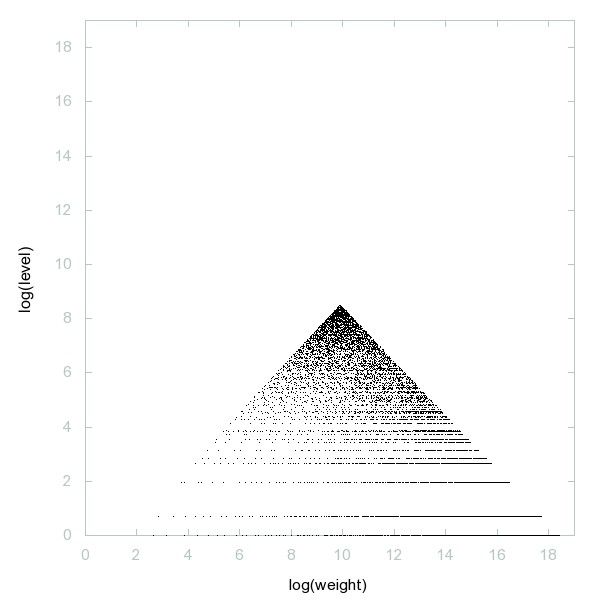
Graphe de log(A020639) vs log(A032742) pour n ≤ 10^4, (graphe sur OEIS):
Décomposition des nombres premiers
[modifier | modifier le wikicode], et sont les seuls nombres premiers non décomposables[1]. Execpté pour , et , la décomposition en poids × niveau + saut des nombres premiers est :
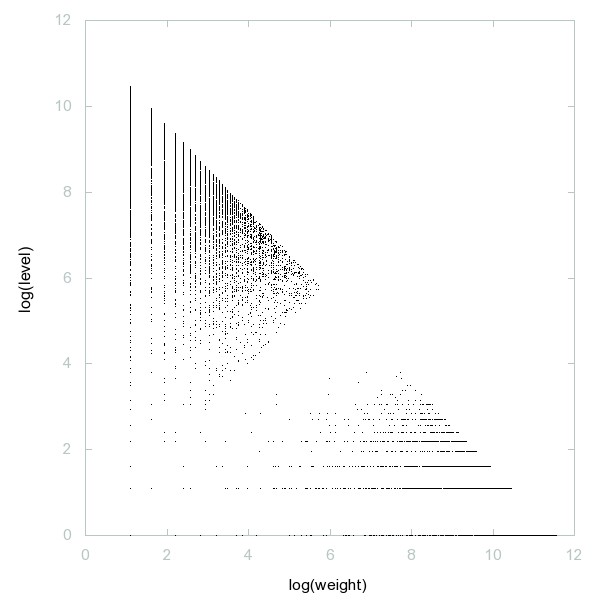
Graphe de log(A117078) vs log(A117563) pour n ≤ 10^4 (graphe sur OEIS):
Une classification des nombres premiers connectée à l'OEIS
[modifier | modifier le wikicode]Nombres premiers de niveau (1;i)
[modifier | modifier le wikicode]Principe de classification pour les nombres premiers de niveau 1:
- Si pour , est un premier dit alors est de niveau (1;i).
- Les nombres premiers de niveau (1;1) sont les balanced primes: (A006562);
- Les nombres premiers de niveau (1;2): A117876;
- Les nombres premiers de niveau (1;3): A118467;
- ...
Relations directes
[modifier | modifier le wikicode]Pour différent de 2, 3 and 7, on a:
Nombres premiers classés par poids
[modifier | modifier le wikicode]Pour les nombres premiers classés par poids (Cf. A162175) (premiers pour lesquels ), on a:
82,89 % des nombres premiers sont classés par poids pour .
On peut voir que par définition les nombres premiers classés par poids suivent la conjecture de Legendre et la conjecture d'Andrica.
Nombres premiers classés par niveau
[modifier | modifier le wikicode]Pour les nombres premiers classés par niveau (Cf. A162174) (premiers pour lesquels ), on a:
17,11 % des nombres premiers sont classés par niveau pour .
Sachant que les nombres premiers se raréfient parmi les entiers naturels et d'après les données numériques, nous faisons la conjecture suivante:
- Conjecture 9: Les premiers classés par niveau se raréfient parmi les nombres premiers.
Plus petit des nombres premiers jumeaux
[modifier | modifier le wikicode]Si est un plus petit nombre premier jumeau plus grand que alors a un poids de . Si a un poids de alors est un plus petit nombre premier jumeau [1]. (voir A001359)
Conjectures
[modifier | modifier le wikicode]La célèbre conjecture sur l’existence d'une infinité de nombres premiers jumeaux peut être reformulée en :
- Conjecture 1: Le nombre de premiers avec un poids de 3 est infini.
Pour étendre cette conjecture, nous faisons les deux conjectures suivantes :
- Conjecture 2: Le nombre de premiers avec un poids de est infini pour tout impair;
- Conjecture 3: Le nombre de premiers avec un niveau de est infini pour tout impair.
- Conjecture 4: Excepté pour p(6) = 13, p(11) = 31, p(30) = 113, p(32) = 131 et p(154) = 887, les premiers classés par niveau on un poids qui est lui-même premier.
La conjecture sur l’existence d'une infinité de "balanced primes" peut être reformulée en :
- Conjecture 5: Le nombres de premiers de niveau(1,1) est infini.
Qui peut être facilement généralisée en :
- Conjecture 6: Le nombres de premiers de niveau(1,i) est infini pour tout .
Sachant que les nombres premiers se raréfient parmi les entiers naturels et suivant les données numériques, nous faisons la conjecture suivante:
- Conjecture 9: Les premiers classés par niveau se raréfient parmi les nombres premiers.
Décomposition des nombres impairs
[modifier | modifier le wikicode]Si la décomposition est possible, on a :
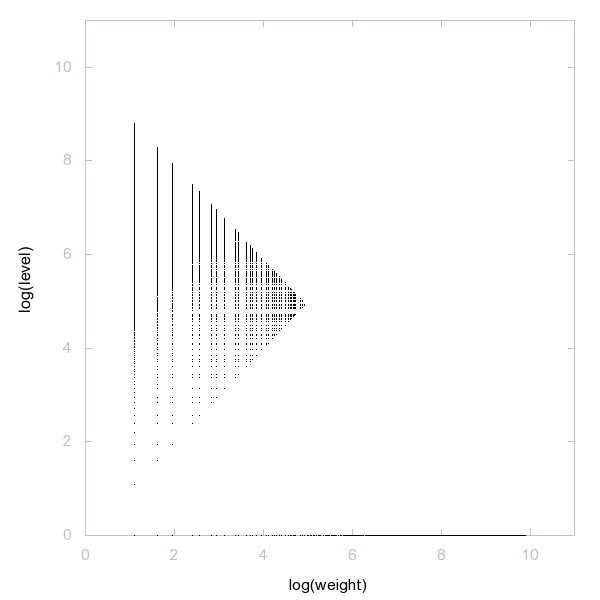
Graphes de log(A090368) vs log(A184726) for n ≤ 10^4 (graphe sur l'OEIS):
Décomposition des nombres pairs
[modifier | modifier le wikicode]Si la décomposition est possible, on a :
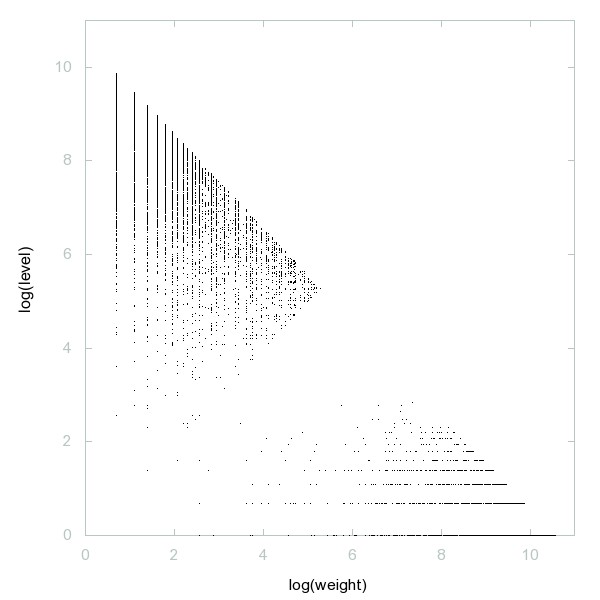
Graphes de log(A090369) vs log(A184727) for n ≤ 10^4 (graphe sur l'OEIS):
Décomposition des nombres composés
[modifier | modifier le wikicode]Si la décomposition est possible, on a :
Graphes de log(A130882) vs log(A179621) for n ≤ 10^4 (graphe sur l'OEIS):
Décomposition des semi-premiers
[modifier | modifier le wikicode]Si la décomposition est possible, on a :
Graphes de log(A130533) vs log(A184729) for n ≤ 10^4 (graphe sur l'OEIS):
Décomposition des 3-presque premiers
[modifier | modifier le wikicode]Si la décomposition est possible, on a :
Graphes de log(A130650) vs log(A184753) for n ≤ 10^4 (graphe sur l'OEIS):
Décomposition des nombres chanceux
[modifier | modifier le wikicode]Si la décomposition est possible, on a :
Graphes de log(A130889) vs log(A184828) for n ≤ 10^4 (graphe sur l'OEIS):
Décomposition des nombres primaires
[modifier | modifier le wikicode]Si la décomposition est possible, on a :
Graphes de log(A184829) vs log(A184831) for n ≤ 10^4 (graphe sur l'OEIS):
Décomposition des nombres sans facteur carré
[modifier | modifier le wikicode]Si la décomposition est possible, on a :
Graphes de log(A184832) vs log(A184834) for n ≤ 10^4 (graphe sur l'OEIS):
Décomposition des nombres triangulaires
[modifier | modifier le wikicode]Si la décomposition est possible, on a :
Graphes de log(A130703) vs log(A184219) for n ≤ 10^4 (graphe sur l'OEIS):
Décomposition des nombres carrés
[modifier | modifier le wikicode]Si la décomposition est possible, on a :
Graphes de log(A133150) vs log(A184221) for n ≤ 10^4 (graphe sur l'OEIS):
Notes
[modifier | modifier le wikicode]- ↑ 1,0 et 1,1 Rémi Eismann, arXiv:0711.0865 [math.NT]: Decomposition into weight * level + jump and application to a new classification of primes (pdf) arXiv:0711.0865(pdf)
Liens externes
[modifier | modifier le wikicode]- arXiv:0711.0865 [math.NT]: Decomposition into weight * level + jump and application to a new classification of primes, 2007 - 2010, Rémi Eismann.
- decompwlj.com : 1000 suites décomposées avec les graphes en 3D (three.js WebGL), 2D, les 500 premiers termes et des exports csv.