Ondes électromagnétiques/Interface diélectrique-métal, ondes stationnaires

Début de la boite de navigation du chapitre

fin de la boite de navigation du chapitre

On se placera dans la jauge de Lorenz. L'origine du repère utilisé est un point O situé à la surface de séparation entre les deux milieux considérés. Le point courant est noté M et repéré par le vecteur ${\overrightarrow {\rm {OM}}}={\vec {r}}$.

Réflexion sur un métal parfait

Lois de Snell-Descartes

Modèle de la surface métallique

On étudie le comportement d'une onde électromagnétique :

• plane
• progressive, se propageant dans la direction ${\vec {u}}_{i}$
• monochromatique, de pulsation ω
• polarisée rectilignement

à l'interface entre :

• un milieu diélectrique LHI d'indice optique n
• un métal parfait

le tout dans les hypothèses suivantes :

• sans charges ni courants volumiques
• milieux non absorbants
• milieux non magnétiques

On note :

• $k_{0}={\frac {\omega }{c}}$ le nombre d'onde dans le vide de cette onde
• $k=n\,k_{0}$ le nombre d'onde de cette même onde dans le délectrique
• ${\vec {n}}$ la normale au dioptre au lieu d'incidence

L'onde incidente a pour vecteur d'onde ${\vec {k}}_{i}=k{\vec {u}}_{i}$. L'angle d'incidence que ${\vec {k}}_{i}$ forme avec la normale au dioptre est noté i.

L'expérience montre qu’il se forme alors une onde réfléchie plane, progressive, monochromatique de même pulsation ω, de vecteur d'onde ${\vec {k}}_{r}=k{\vec {u}}_{r}$. L'angle d'incidence que ${\vec {k}}_{r}$ forme avec la normale au dioptre est noté i'.

Au niveau de la surface de séparation, les champs électrique et magnétique, incident et réfléchi s'écrivent sous la forme générale :

• ${\vec {s}}_{i}({\vec {r}},t)={\vec {s}}_{0i}e^{j(\omega t-{\vec {k}}_{i}\cdot {\vec {r}})}$
• ${\vec {s}}_{r}({\vec {r}},t)={\vec {s}}_{0r}e^{j(\omega t-{\vec {k}}_{r}\cdot {\vec {r}})}e^{j\varphi _{r}}$
• $\varphi _{r}$ ne dépend pas de ${\vec {r}}$

Le déphasage entre l'onde réfléchie et l'onde incidente vaut $({\vec {k}}_{i}-{\vec {k}}_{r})\cdot {\vec {r}}+\varphi _{r}$, qui doit être indépendant de ${\vec {r}}$. Par le même raisonnement que dans le chapitre précédent, on aboutit aux lois suivantes :

Début d’un théorème

Lois de Snell-Descartes

• 1° loi de Descartes : ${\vec {n}},~{\vec {u}}_{i},~{\vec {u}}_{r}$ sont dans un même plan
• 2° loi de Descartes de la réflexion : $i=-i'$

Fin du théorème

Incidence normale et courant surfacique

Dans cette section, on se place dans le cas simplifié où l'onde incidente est normale au dioptre. On a alors :

${\begin{cases}i=0\\i'=0\end{cases}}$

On se place dans la base $({\vec {u}}_{x},{\vec {u}}_{y},{\vec {u}}_{z})$ telle que :

• l'onde incidente soit polarisée rectilignement suivant ${\vec {u}}_{y}$
• le vecteur d'onde de l'onde réfléchie ait même sens et même direction que ${\vec {u}}_{z}$

L'onde incidente a

• pour vecteur d'onde ${\vec {k}}_{i}=-nk_{0}{\vec {u}}_{z}$
• pour champ électrique ${\vec {E}}_{i}=E_{0i}e^{j(\omega t+nk_{0}z)}{\vec {u}}_{y}$
• pour champ magnétique ${\vec {B}}_{i}=B_{0i}e^{j(\omega t+nk_{0}z)}{\vec {u}}_{x}$, où $B_{0i}=n{\frac {E_{0i}}{c}}$

L'onde réfléchie a

• pour vecteur d'onde ${\vec {k}}_{r}=nk_{0}{\vec {u}}_{z}$
• pour champ électrique ${\vec {E}}_{r}={\vec {E}}_{0r}e^{j(\omega t-nk_{0}z)}e^{j\varphi _{r}}$
• pour champ magnétique ${\vec {B}}_{r}={\vec {B}}_{0r}e^{j(\omega t-nk_{0}z)}e^{j\varphi _{r}}$ avec ${\vec {B}}_{0r}={\frac {n}{c}}{\vec {u}}_{z}\wedge {\vec {E}}_{0r}$

Les équations de passage donnent :

• Pour le champ électrique : $E_{0i}{\vec {u}}_{y}e^{j\omega t}+{\vec {E}}_{0r}e^{j\varphi _{r}}e^{j\omega t}={\frac {\sigma }{\epsilon _{0}}}{\vec {u}}_{z}$
• Pour le champ magnétique : $n{\frac {E_{0i}}{c}}e^{j\omega t}{\vec {u}}_{x}+{\frac {n}{c}}{\vec {u}}_{z}\wedge {\vec {E}}_{0r}e^{j\varphi _{r}}e^{j\omega t}=\mu {\vec {j}}_{S}\wedge {\vec {u}}_{z}$

Dans la première équation, on remarque que $E_{0i}{\vec {u}}_{y}e^{j\omega t}+{\vec {E}}_{0r}e^{j\varphi _{r}}e^{j\omega t}\perp {\vec {u}}_{z}$, donc $\sigma =0$.

Cela entraîne $E_{0i}{\vec {u}}_{y}=-{\vec {E}}_{0r}e^{j\varphi _{r}}$, donc :

${\begin{cases}{\vec {E}}_{0i}={\vec {E}}_{0r}\\\varphi _{r}=\pi \end{cases}}$

On réinjecte cette information dans la deuxième équation :

${\begin{aligned}\mu {\vec {j}}_{S}\wedge {\vec {u}}_{z}&={\frac {n}{c}}e^{j\omega t}\left(E_{0i}{\vec {u}}_{x}-{\vec {u}}_{z}\wedge {\vec {u}}_{y}E_{0i}\right)\\&={\frac {2nE_{0i}{\vec {u}}_{x}}{c}}e^{j\omega t}\end{aligned}}$

Faites ces exercices : Propagation dans un métal réel.

Début d’un théorème

Courant surfacique

L'incidence de l'onde électromagnétique sur le métal fait naître un courant surfacique ${\vec {j}}_{S}={\frac {2n}{\mu c}}{\vec {E}}_{0i}e^{j\omega t}$.

Ce courant :

• a même pulsation que l'onde
• est proportionnel au champ électrique incident
• a même direction que ce champ électrique incident

Fin du théorème

Le métal étant supposé parfaitement conducteur, ce courant n'engendre pas de dissipation de puissance dans le métal. De plus, le champ électromagnétique est parfaitement réfléchi. Dans le cas d'un métal réel, les choses sont différentes car une partie du champ est transmise dans le métal et une partie de l'énergie y est perdue. Une étude plus approfondie de ce cas est laissée en exercice.

Ondes stationnaires

Apparition

Toujours dans l'hypothèse de l'incidence normale, exprimons le champ électromagnétique dans le milieu diélectrique :

• ${\underline {\vec {E}}}={\vec {E}}_{i}+{\vec {E}}_{r}=2j\sin(nk_{0}z)E_{0i}e^{j\omega t}{\vec {u}}_{y}$
• ${\underline {\vec {B}}}={\vec {B}}_{i}+{\vec {B}}_{t}=2\cos(nk_{0}z)B_{0i}e^{j\omega t}{\vec {u}}_{x}$

Soit, en prenant la partie réelle :

${\begin{cases}{\vec {E}}=2E_{0i}\sin(nk_{0}z)\cos \left(\omega t+{\frac {\pi }{2}}\right)\\{\vec {B}}=2B_{0i}\cos(nk_{0}z)\cos(\omega t)\\\end{cases}}$

Onde stationnaire

Dans les expressions du champ électromagnétique dans le diélectrique, le temps et les coordonnées d'espace ne sont plus en argument de la même fonction.

L'onde ne se propage plus : on ne parle alors plus d'onde progressive mais d'onde stationnaire.

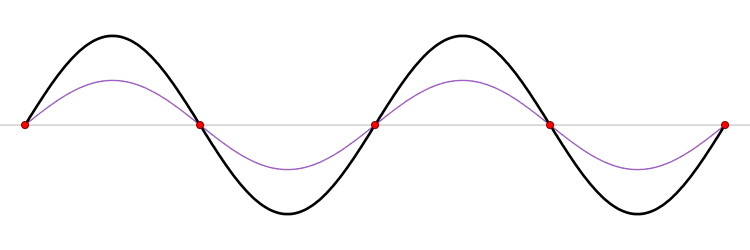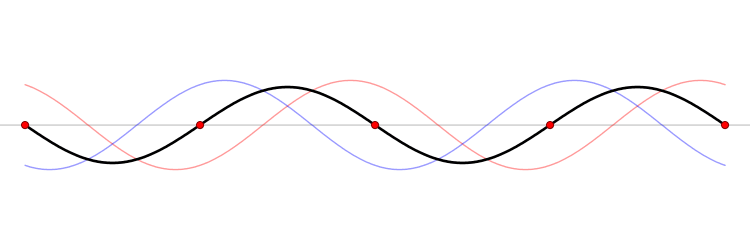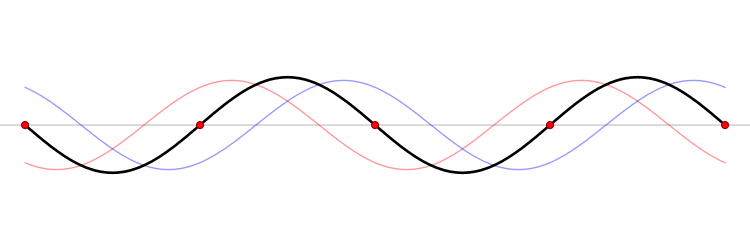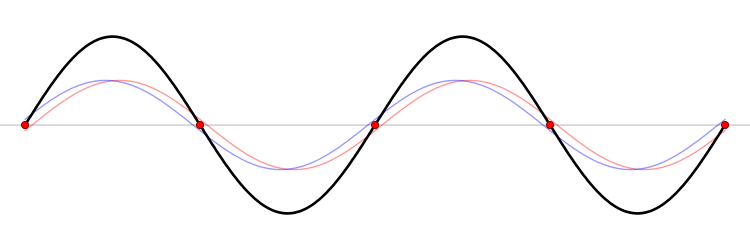
On peut visualiser ce résultat sur l'animation ci-dessous, qui représente la superposition des deux ondes se propageant dans le diélectrique :

• l'onde rouge joue le rôle de l'onde incidente, se propageant vers la gauche,
• l'onde bleue joue le rôle de l'onde réfléchie, se propageant vers la droite,
• la superposition est représentée en noir.

Onde stationnaire entre deux plans parallèles : Quantification du vecteur d'onde

On considère deux plans constitués de métaux parfaits, parallèles, d'équations $z=0$ et $z=L$, séparés par un milieu diélectrique d'indice optique n dans lequel la célérité des ondes électromagnétiques vaut v. On cherche à établir une onde électromagnétique stationnaire entre ces deux plans.

On sait que le potentiel vecteur vérifie l'équation ${\vec {\Delta }}{\vec {A}}={\frac {1}{v^{2}}}{\frac {\partial ^{2}{\vec {A}}}{\partial t^{2}}}$. Au vu de la symétrie du système, on cherche les solutions sous la forme ${\vec {A}}=A(z)e^{j\omega t}{\vec {u}}_{x}$.

L'équation différentielle devient ${\frac {{\rm {d}}^{2}A}{{\rm {d}}z^{2}}}+{\frac {\omega ^{2}}{v^{2}}}A(z)=0$

Les solutions sont donc de la forme $A(z)=A_{0}\sin \left({\frac {\omega }{v}}z+\varphi \right)=A_{0}\sin(kz+\varphi )$

Les conditions aux limites sont dictées par le fait que les métaux sont parfaits :

${\begin{cases}A(0)=0\\A(L)=0\end{cases}}$

Donc

${\begin{cases}A_{0}\sin(\varphi )=0\\A_{0}\sin(kL+\varphi )=0\end{cases}}\Rightarrow {\begin{cases}\varphi =0\\A_{0}\sin(kL)=0\end{cases}}$

On déduit de la deuxième égalité que $\exists m\in \mathbb {N} ^{*},~kL=m\pi$

Faites ces exercices : Ondes stationnaires.

Quantification du vecteur d'onde

Le vecteur d'onde est quantifié : $k={\frac {m\pi }{L}},~m\in \mathbb {N} ^{*}$.

Ainsi, entre deux plans, on ne pourra établir que des ondes de fréquence déterminée.

Modes d'une corde vibrante

En termes de longueur d'onde, la quantification s'écrit $L=m{\frac {\lambda }{2}},~m\in \mathbb {N} ^{*}$. On retrouve ainsi le même résultat que pour les modes d'une corde électrique vibrante entre deux points : les seuls modes pouvant s'établir sont les modes pour lesquels la largeur de la cavité est un multiple de la demi-longueur d'onde.

→ Cette quantification du vecteur d'onde est la base de la théorie des ondes électromagnétiques guidées et des guides d'ondes. C'est également la cause de l’effet Casimir.

→ En mécanique quantique, on retrouve exactement la même problématique pour le cas d'une particule dans un puits de potentiel.

Forme des champs

Du potentiel vecteur, on déduit le champ électromagnétique :

${\begin{cases}{\vec {B}}=A_{0}k\cos(kz)\cos(\omega t){\vec {u}}_{y}\\{\vec {E}}=A_{0}\omega \sin(kz)\sin(\omega t){\vec {u}}_{x}\end{cases}}$

Topologiquement, on constate que les nœuds du champ électrique sont les ventres du champ magnétique et vice-versa.

De plus, au cours du temps, les champs électrique et magnétique s'échangent de l'énergie : lorsque le champ électrique est identiquement nul dans la cavité, le champ magnétique est maximal et vice-versa.