Miroirs en optique géométrique/Miroirs sphériques

Centre et sommet
[modifier | modifier le wikicode]Les miroirs sphériques sont des portions de calottes sphériques. Ils peuvent être concaves ou convexes. On note souvent C le centre de la sphère et R son rayon.
Dans le cas d’un système centré, on peut placer un miroir sphérique dont le centre est sur l’axe optique (on a ainsi la symétrie par révolution). L'intersection S entre le miroir et l’axe optique est appelé sommet du miroir.
La première chose que l’on peut remarquer est que l’image du centre est le centre, et l’image du sommet est le sommet. En effet, un rayon issu de C est réfléchi en direction de C, et tout rayon issu de S passe automatiquement par ce même point. Cela est illustré par les quatre images suivantes :

|
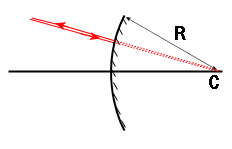
|
| Centre d’un miroir concave. | Centre d’un miroir convexe. |

|

|
| Sommet d’un miroir concave. | Sommet d’un miroir convexe. |
On voit donc que le stigmatisme est rigoureux pour le centre et le sommet, mais ce n’est pas le cas pour les autres points ! On va maintenant utiliser les conditions de Gauss pour avoir un stigmatisme approché.
Stigmatisme approché, relation de conjugaison
[modifier | modifier le wikicode]
On commence par étudier le cas d’un miroir concave. On considère un objet A et son image A' comme le montre l’image ci-contre. On veut alors que le système soit stigmatique, c'est-à-dire que quelle que soit la position du point I, le rayon passe toujours par le même point A' . Comme on va le voir, les conditions de Gauss sont nécessaires.
Dans les triangles AIC et CIA' , les sommes des angles donnent respectivement : α + i + π − β = π et β + i + π − θ = π, ce que l’on peut réécrire par α + i = β et β + i = θ. En soustrayant ces deux relations, on obtient : α − β = β − θ d'où .
D'autre part, on calcule les tangentes de ces trois angles : , et . Or lorsqu'on se place dans les conditions de Gauss les angles sont supposés petits. Ainsi on sait que (même chose pour β et θ). De plus, comme le point I est très proche de l’axe optique, on peut pratiquement assimiler H à S. Les relations précédentes deviennent donc : , et .
Donc en utilisant la relation α + θ = 2 β, puis en divisant le tout par , on obtient :
Ces relations sont très importantes car elles sont aussi valables pour un miroir sphérique convexe.
On a donc effectivement montré que dans les conditions de Gauss, il y a un stigmatisme approché.
La relation de conjugaison donnée ci-dessus est effectuée par rapport au sommet S. Il est possible de transformer cette relation pour utiliser le foyer à la place du sommet (ce sera fait en exercice). Le résultat est le suivant :
Foyers
[modifier | modifier le wikicode]- Foyer objet
Le foyer objet F d’un miroir sphérique est, par définition, le point de l’axe optique dont l’image est à l'infini, c'est-à-dire ou encore . Or le foyer vérifie la relation de conjugaison : donc et finalement
|
Le foyer objet d’un miroir est à équidistance du centre et du sommet. |
Cela est illustré par les images suivantes dans le cas d’un miroir concave puis convexe.

|

|
On remarque effectivement que les rayons issus de F sont toujours renvoyés à l'infini (c'est la définition du foyer objet).
- Foyer image
Le même raisonnement est applicable pour le foyer image F' . On obtient alors ce qui est identique à la relation obtenue pour F.
|
Les foyers objet et image d’un miroir sphérique sont confondus. |

|

|
Distance focale
[modifier | modifier le wikicode]Pour un miroir sphérique, on définit :
- la distance focale objet ,
- la distance focale image .
Les paragraphes précédents nous permettent donc d'écrire :
- pour un miroir concave,
- pour un miroir convexe.
























