Conduction thermique/Équation de la chaleur

Début de la boite de navigation du chapitre

fin de la boite de navigation du chapitre

Équation de la chaleur

L'équation de la chaleur s'écrit en toute généralité :

${\partial T \over \partial t}={\lambda \over c_{v}\rho }{\vec {\nabla }}^{2}T+{p \over c_{v}\rho }$

où

• T est la température ;
• λ est la conductivité thermique ;
• c_v est la capacité thermique massique à volume constant ;
• ρ est la masse volumique ;
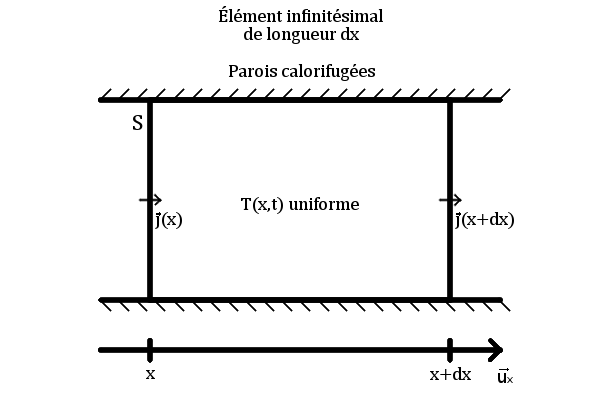
• $\nabla$est nabla et ${\vec {\nabla }}^{2}$est le laplacien ;
• p est la puissance volumique dégagée (par exemple dans le cas d'un résistor, p est la puissance dissipée par effet Joule).

Démonstration à une dimension

Élément infinitésimal à une dimension

On applique le premier principe à un petit élément de longueur $\operatorname {d} \!x$, en considérant que les échanges thermiques :

$\operatorname {d} \!U=\partial Q+p\operatorname {d} \!t$

$p\operatorname {d} \!t$est l'énergie volumique dégagée pendant un temps $\operatorname {d} \!t$

Dans le cas d'une phase condensée (on écrit alors que c_v = c = c_p) ou un gaz parfait :

$\operatorname {d} \!U=m*c_{v}\operatorname {d} \!T$

Donc par définition de j, densité de flux thermique

$m*c_{v}{\partial T \over \partial t}\operatorname {d} \!t=j(x)S\operatorname {d} \!t-j(x+dx)S\operatorname {d} \!t+p\operatorname {d} \!t$

où S est la surface.

Par définition de la différentielle et par simplification par $\operatorname {d} \!t$

${\partial T \over \partial t}=-{S \over m*c_{v}}{\partial j \over \partial x}\operatorname {d} \!x+{p \over m*c_{v}}$

Par définition de la masse volumique $\rho ={m \over \partial V}$et du petit volume considéré $\partial V=S\operatorname {d} \!x$

De plus la loi de Fourier donne ${\vec {j}}=-\lambda {\vec {\nabla }}T$, où ${\vec {\nabla }}T$est le gradient de la température qui sécrit en une dimension :

${\vec {\nabla }}T={\partial T \over \partial x}$

Finalement

${\partial T \over \partial t}={\lambda \over \ \rho c_{v}}{\partial ^{2}T \over \partial x^{2}}+{p \over \rho c_{v}}$

On peut alors généraliser de la même façon à trois dimensions.