Calcul avec les nombres complexes/Représentation géométrique

**Représentation géométrique**
Leçon : Calcul avec les nombres complexes

Chapitre n^o 3
Chap. préc. :	Opérations sous forme algébrique
Chap. suiv. :	Conjugué d'un nombre complexe

En raison de limitations techniques, la typographie souhaitable du titre, « Calcul avec les nombres complexes : Représentation géométrique
Calcul avec les nombres complexes/Représentation géométrique », n'a pu être restituée correctement ci-dessus.

Pour comprendre les nombres complexes, il faut pouvoir les visualiser dans un espace que nous connaissons au préalable. Le problème est que ces nombres complexes n'ont pas de représentation physique, nous ne pouvons par exemple les ordonner sur une règle, chose facile à faire pour les nombres réels.

Néanmoins, le plan complexe (appelé aussi plan d'Argand ou plan d'Argand-Cauchy) permet de résoudre ce problème.

Affixe d’un point du plan[modifier | modifier le wikicode]

Définition

Dans le plan muni d’un repère orthonormé, on associe au point M de coordonnées $(a,b)$

son affixe, le nombre complexe $z=a+\mathrm {i} b$ . M est appelé image de $z$

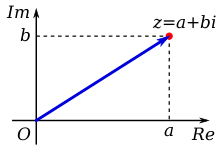
On a ainsi une correspondance entre les nombres complexes et les points du plan, qui permet de représenter géométriquement les nombres complexes :

la partie réelle du nombre complexe est l'abscisse de son image ;
sa partie imaginaire est l'ordonnée de son image.

Graphiquement, on obtient :

Exemple

Dans le graphique ci-contre, on assimile les nombres complexes à leurs images. Par exemple :

le point de coordonnées $(3,-4)$ et son affixe, le nombre complexe $z_{4}=3-4\mathrm {i}$ .

Affixe d’un vecteur[modifier | modifier le wikicode]

Définition

Au vecteur ${\vec {u}}$ de coordonnées ${\begin{array}{|l}x\\y\\\end{array}}$ , on associe son affixe $z=x+\mathrm {i} y$ .

Propriétés de l'affixe[modifier | modifier le wikicode]

Affixe d’un vecteur[modifier | modifier le wikicode]

Propriété

L'affixe d’un vecteur ${\overrightarrow {AB}}$ est : $z_{\overrightarrow {AB}}=z_{B}-z_{A}$ .

Exemple

Dans la figure ci-contre, on a les points $A(1,1)$ et $B(4,3)$ .

L'affixe d’un vecteur ${\overrightarrow {AB}}$ est : $z_{\overrightarrow {AB}}=z_{B}-z_{A}=(4+3\mathrm {i} )-(1+\mathrm {i} )=3+2\mathrm {i}$ .

En effet, les coordonnées de ${\overrightarrow {AB}}$ sont :

${\begin{array}{|l}x_{B}-x_{A}\\y_{B}-y_{A}\end{array}}={\begin{array}{|l}4-1\\3-1\end{array}}={\begin{array}{|l}3\\2\end{array}}$ .

Affixe d’un milieu[modifier | modifier le wikicode]

Propriété

L'affixe du milieu $I$ d’un segment $[AB]$ est $z_{I}=z_{\overrightarrow {OI}}={\frac {z_{B}+z_{A}}{2}}$ .

Exemple

Toujours dans la figure ci-contre dont les points $A$ et $B$ ont pour coordonnées respectives $(1,1)$ et $(4,3)$ .

${\overrightarrow {OI}}$ , l'affixe du milieu du vecteur ${\overrightarrow {AB}}$ est : $z_{\overrightarrow {OI}}={\frac {z_{B}+z_{A}}{2}}={\frac {(4+3\mathrm {i} )+(1+\mathrm {i} )}{2}}={\frac {5+4\mathrm {i} }{2}}={\frac {5}{2}}+2\mathrm {i}$ .

Les coordonnées de ${\overrightarrow {OI}}$ sont :

${\begin{array}{|l}\displaystyle {\frac {x_{B}+x_{A}}{2}}\\\displaystyle {\frac {y_{B}+y_{A}}{2}}\end{array}}={\begin{array}{|l}\displaystyle {\frac {4+1}{2}}\\\displaystyle {\frac {3+1}{2}}\end{array}}={\begin{array}{|l}\displaystyle {\frac {5}{2}}\\2\end{array}}$ .

Parallélisme et alignement[modifier | modifier le wikicode]

Propriété

Deux droites $(AB)$ et $(CD)$ sont parallèles si et seulement si les vecteurs ${\overrightarrow {AB}}$ et ${\overrightarrow {CD}}$ sont colinéaires, c'est-à-dire s'il existe un réel $k$ (non nul) tel que ${\overrightarrow {AB}}=k\;{\overrightarrow {CD}}$ , ce qui équivaut à : $\operatorname {Im} \left({\frac {z_{B}-z_{A}}{z_{D}-z_{C}}}\right)=0$ .