Étude et tracé d'une fonction/Exercices/Problèmes divers (2)

Exercice 9-1

1°  Construire la courbe C d'équation :

$y={\frac {x-1}{x^{2}+1}}$

dans un repère R.

2°  Soit A, le point de coordonnées (0,-1). On coupe C par une droite D contenant A et de coefficient directeur m. Formez l'équation du second degré dont les solutions sont les abscisses des points communs à C et D, autres que A.

3°  Démontrer que, entre les solutions de l'équation obtenue, il y a une relation indépendante de m.

4°  Passe-t-il par A des tangentes à C ? Si oui, lesquelles ?

Solution

1°

Domaine de définition

Le dénominateur :

$x^{2}+1$

ne peut pas être nul. Par conséquent :

$D_{f}=\mathbb {R}$

Limites aux bornes du domaine de définition

$\lim _{x\to +\infty }f(x)=\lim _{x\to +\infty }{\frac {x-1}{x^{2}+1}}=\lim _{x\to +\infty }{\frac {x}{x^{2}}}=\lim _{x\to +\infty }{\frac {1}{x}}=0$

$\lim _{x\to -\infty }f(x)=\lim _{x\to -\infty }{\frac {x-1}{x^{2}+1}}=\lim _{x\to -\infty }{\frac {x}{x^{2}}}=\lim _{x\to -\infty }{\frac {1}{x}}=0$

Calcul de la dérivée

$f'(x)={\frac {1\times (x^{2}+1)-2x(x-1)}{(x^{2}+1)^{2}}}={\frac {x^{2}+1-2x^{2}+2x}{(x^{2}+1)^{2}}}={\frac {-x^{2}+2x+1}{(x^{2}+1)^{2}}}$

Les valeurs qui annulent la dérivée sont donc les racines de l'équation :

$-x^{2}+2x+1=0$

on trouve :

${\begin{cases}x_{1}=1-{\sqrt {2}}\\x_{2}=1+{\sqrt {2}}\end{cases}}$

Le minimum est :

$f(x_{1})=f(1-{\sqrt {2}})={\frac {(1-{\sqrt {2}})-1}{(1-{\sqrt {2}})^{2}+1}}={\frac {-{\sqrt {2}}}{1-2{\sqrt {2}}+2+1}}={\frac {-{\sqrt {2}}}{4-2{\sqrt {2}}}}={\frac {-{\sqrt {2}}(2+{\sqrt {2}})}{2(2-{\sqrt {2}})(2+{\sqrt {2}})}}={\frac {-2{\sqrt {2}}-2}{2(4-2)}}={\frac {-{\sqrt {2}}-1}{2}}$

Par un calcul très similaire, on trouve que le maximum est :

$f(x_{2})={\frac {{\sqrt {2}}-1}{2}}$

Tableau de variations

Études des asymptotes

$\lim _{x\to \pm \infty }f(x)=0$ nous indique que nous avons une asymptote horizontale d'équation $y=0$. L'axe des abscisses est donc une asymptote

Tracé de la courbe

2°

L'ordonnée à l'origine d'une droite dans un repère est donnée par l'interception de la droite avec l'axe des ordonnées qui est ici le point A(0;-1), l'équation de la droite D passant par A et de coefficient directeur m sera :

$y=mx-1$

Pour avoir l'équation du second degré dont les solutions sont les abscisses des points communs à C et D, autres que A, il nous suffit de résoudre :

${\frac {x-1}{x^{2}+1}}=mx-1$

qui s'écrit :

$x-1=(mx-1)(x^{2}+1)$

En développant le second membre et en mettant tous les termes dans un même membre, on obtient :

$mx^{3}-x^{2}+(m-1)x=0$

x = 0 est solution de cette équation et correspond à l'abscisse de A. Comme nous recherchons des points autre que A, nous éliminerons cette possibilité en simplifiant l'équation par x, nous obtenons :

$mx^{2}-x+(m-1)=0$

qui est l'équation du second degré recherchée.

3°

L'équation :

$mx^{2}-x+(m-1)=0$

est du second degré et admettra donc deux solutions x₁ et x₂ (éventuellement confondues) lorsque son discriminant :

$(-1)^{2}-4m(m-1)=-4m^{2}+4m+1$

sera positif ou nul.

Dans ce cas, nous aurons :

${\begin{cases}x_{1}+x_{2}={\frac {1}{m}}\\x_{1}.x_{2}={\frac {m-1}{m}}\end{cases}}$

Où l'on voit que :

$x_{1}.x_{2}={\frac {m-1}{m}}=1-{\frac {1}{m}}=1-(x_{1}+x_{2})$

Et l'on a obtenu la relation indépendante de m suivante :

$x_{1}.x_{2}+x_{1}+x_{2}=1$

4°

Une première méthode intuitive (et pas très rigoureuse d'un point de vue mathématique) consiste, à partir du tracé de la courbe, à imaginer l'ensemble des droites passant par A(0;-1). On voit aisément qu'il y a la plupart du temps, soit deux points d'interception avec C soit aucun point d'interception. Toutefois, à la limite entre ces deux groupes de droites semble se trouver des droites qui visiblement sont tangentes à la courbe et n'ont qu'un seul point d'interception avec celle-ci et, dans le groupe où il y a deux points d'interception, en faisant tendre la droite vers la droite limite, on voit que les deux points d'interception tendent l'un vers l'autre pour se confondre au point de tangence. Ce raisonnement intuitif nous amène à penser que les abscisses des points de tangence sont obtenus à partir de la relation :

$x_{1}.x_{2}+x_{1}+x_{2}=1$

en posant :

$x_{1}=x_{2}=t$

et on obtient :

$t.t+t+t=1$

Soit l'équation :

$t^{2}+2t-1=0$

dont les solutions sont :

${\begin{cases}t_{1}=-1-{\sqrt {2}}\\t_{2}=-1+{\sqrt {2}}\end{cases}}$

abscisses de deux points dont la tangente passe par A.

Si l'on veut traiter la question de façon plus rigoureuse, on peut imaginer un point M d'abscisse t appartenant à la courbe. Calculons l'équation de la tangente en M à la courbe, nous obtenons :

$y=f'(t)(x-t)+f(t)$

qui donne :

$y={\frac {-t^{2}+2t+1}{(t^{2}+1)^{2}}}(x-t)+{\frac {t-1}{t^{2}+1}}$

Parmi toutes ces tangentes, essayons de calculer les valeurs de t telles que la tangente passera par A de coordonnées (0;-1). En remplaçant x par 0 et y par -1, on obtient :

$-1={\frac {-t^{2}+2t+1}{(t^{2}+1)^{2}}}(-t)+{\frac {t-1}{t^{2}+1}}$

après réduction au même dénominateur, on obtient :

$-1={\frac {2t^{3}-3t^{2}-1}{(t^{2}+1)^{2}}}$

Qui s'écrit :

$-(t^{2}+1)^{2}=2t^{3}-3t^{2}-1$

En développant et en mettant tous les termes dans un même membre, nous sommes amenés à résoudre l'équation :

$t^{4}+2t^{3}-t^{2}=0$

qui se factorise sous la forme :

$t^{2}(t^{2}+2t-1)=0$

dont les solutions sont :

${\begin{cases}t_{1}=-1-{\sqrt {2}}\\t_{2}=-1+{\sqrt {2}}\\t_{3}=0\end{cases}}$

abscisses des trois points dont la tangente passe par A.

Si dans la première méthode intuitive, nous n'avions pas obtenu le point A comme solution, c'est parce que nous avions raisonné à partir de la relation :

$x_{1}.x_{2}+x_{1}+x_{2}=1$

qui avait été obtenue en excluant le point A comme interception de D et C.

La première méthode, en plus d'être intuitive, était donc bien mathématiquement incorrecte. Si nous l'avons exposée, c'est parce que les questions précédentes semblaient nous engager à le faire (était-ce un piège ?).

 

Exercice 9-2

1°  Tracez sur un même graphique les courbes C et T données par leur équation :

${\begin{cases}C\,:\;y^{2}=2x\\T\,:\;y^{2}={\frac {8}{27}}(x-1)^{3}\end{cases}}$

2°  Déterminer l'équation de la tangente Δ à T au point d'abscisse 2 et d'ordonnée positive.

3°  Δ rencontre C en deux points P et P'. Calculer l'abscisse du point A, interception des tangentes à C en P et en P'.

Solution

1°

Compte tenu de la présence de y² dans le premier membre des équations, nous devons, pour nous ramener à des fonctions, extraire les racines carrées des seconds membres. Ce qui nous donne :

${\begin{cases}C\,:\;y=\pm {\sqrt {2x}}\\T\,:\;y=\pm {\sqrt {{\frac {8}{27}}(x-1)^{3}}}\end{cases}}$

Et nous voyons que nous avons en réalité quatre fonctions à tracer.

${\begin{cases}f_{1}(x)={\sqrt {2x}}\\f_{2}(x)=-{\sqrt {2x}}\\f_{3}(x)={\sqrt {{\frac {8}{27}}(x-1)^{3}}}\\f_{4}(x)=-{\sqrt {{\frac {8}{27}}(x-1)^{3}}}\end{cases}}$

Le tracé nous donne :

• Le tracé de f₁ correspond à la partie de C qui est au-dessus de l'axe des abscisses.
• Le tracé de f₂ correspond à la partie de C qui est au-dessous de l'axe des abscisses.
• Le tracé de f₃ correspond à la partie de T qui est au-dessus de l'axe des abscisses.
• Le tracé de f₄ correspond à la partie de T qui est au-dessous de l'axe des abscisses.

2°

Compte tenu des spécifications de l'énoncé, nous devons considérer la fonction f₃. Le calcul de la dérivée nous donne :

$f_{3}'(x)={\sqrt {\frac {2(x-1)}{3}}}$

L'équation de la tangente au point d'abscisse 2 s'écrira donc :

$y=f_{3}'(2)(x-2)+f_{3}(2)$

Soit :

$y={\sqrt {\frac {2(2-1)}{3}}}(x-2)+{\sqrt {{\frac {8}{27}}(2-1)^{3}}}$

qui se simplifie en :

$y={\sqrt {\frac {2}{3}}}(x-2)+{\frac {2}{3}}{\sqrt {\frac {2}{3}}}$

et on obtient comme équation de la tangente Δ à T au point d'abscisse 2 et d'ordonnée positive :

$y={\sqrt {\frac {2}{3}}}\left(x-{\frac {4}{3}}\right)$

3°

Pour trouver les abscisses de P et P', nous devons résoudre le système formé par les équations de Δ et C :

${\begin{cases}y={\sqrt {\frac {2}{3}}}\left(x-{\frac {4}{3}}\right)\\y^{2}=2x\end{cases}}$

En tirant y de la première équation et en portant dans la deuxième, on obtient :

$\left[{\sqrt {\frac {2}{3}}}\left(x-{\frac {4}{3}}\right)\right]^{2}=2x$

En développant le premier membre :

${\frac {2}{3}}\left(x^{2}-{\frac {8}{3}}x+{\frac {16}{9}}\right)=2x$

qui donne finalement :

$9x^{2}-51x+16=0$

En résolvant cette équation de second degré, on trouve :

${\begin{cases}x_{1}={\frac {1}{3}}\\x_{2}={\frac {16}{3}}\end{cases}}$

Nous voyons que :

P est sur le tracé de f₂ et a pour abscisse 1/3

P' est sur le tracé de f₁ et a pour abscisse 16/3

(voir éventuellement le schéma ci-dessous avec les tangentes)

Calculons la tangente à C passant par P :

L'équation de cette tangente est :

$y=f_{2}'\left({\frac {1}{3}}\right)\left(x-{\frac {1}{3}}\right)+f_{2}\left({\frac {1}{3}}\right)$

Le calcul de la dérivée de f₂ donne :

$f_{2}'(x)=-{\frac {1}{\sqrt {2x}}}$

L'équation de la tangente s'écrira donc :

$y=-{\sqrt {\frac {3}{2}}}\left(x-{\frac {1}{3}}\right)-{\sqrt {\frac {2}{3}}}$

qui se simplifie sous la forme :

$y=-x{\sqrt {\frac {3}{2}}}+{\frac {1}{\sqrt {6}}}-{\frac {2}{\sqrt {6}}}$

et finalement donne :

$y=-{\frac {3x+1}{\sqrt {6}}}$

Calculons la tangente à C passant par P' :

L'équation de cette tangente est :

$y=f_{1}'\left({\frac {16}{3}}\right)\left(x-{\frac {16}{3}}\right)+f_{1}\left({\frac {16}{3}}\right)$

Le calcul de la dérivée de f₁ donne :

$f_{1}'(x)={\frac {1}{\sqrt {2x}}}$

L'équation de la tangente s'écrira donc :

$y={\frac {1}{4}}{\sqrt {\frac {3}{2}}}\left(x-{\frac {16}{3}}\right)+4{\sqrt {\frac {2}{3}}}$

qui se simplifie sous la forme :

$y={\frac {x}{4}}{\sqrt {\frac {3}{2}}}-{\frac {16}{4{\sqrt {6}}}}+{\frac {8}{\sqrt {6}}}$

et finalement donne :

$y={\frac {3x+16}{4{\sqrt {6}}}}$

Si l'on rajoute, sur le schéma, les trois tangentes dont nous avons calculé les équations précédemment, nous obtenons :

Pour calculer l'abscisse du point d'interception A des tangentes à C en P et en P', il suffit alors de résoudre le système :

${\begin{cases}y=-{\frac {3x+1}{\sqrt {6}}}\\y={\frac {3x+16}{4{\sqrt {6}}}}\end{cases}}$

On en déduit :

$-{\frac {3x+1}{\sqrt {6}}}={\frac {3x+16}{4{\sqrt {6}}}}$

Qui se simplifie en :

$4(3x+1)=-3x-16$

d'où l'on tire l'abscisse de A :

$x=-{\frac {4}{3}}$

On peut calculer l'ordonnée de A en utilisant l'équation de l'une des deux tangentes, on trouve :

$y={\sqrt {\frac {3}{2}}}$

Le point A a donc pour coordonnées : $\left(-{\frac {4}{3}};\;{\sqrt {\frac {3}{2}}}\right)$

 

Exercice 9-3

Soit C_a la courbe représentative de la fonction f_a définie par :

$f_{a}(x)=ax+2+{\frac {4}{x}}$

Indiquer les différentes formes des courbes C_a suivant les valeurs de a. (Représenter soigneusement une courbe de chaque forme.)

Solution

Le domaine de définition de f_a est :

$D_{f_{a}}=\mathbb {R} ^{*}=]-\infty ;\;0[\cup ]0;\;+\infty [$

Pour le calcul des limites aux bornes du domaine de définition, nous voyons que nous avons déjà une première distinction à faire selon que a est positif, négatif ou nul.

Si a est positif, nous avons :

$\lim _{x\to +\infty }f_{a}(x)=\lim _{x\to +\infty }ax+2+{\frac {4}{x}}=\lim _{x\to +\infty }ax=+\infty$

$\lim _{x\to -\infty }f_{a}(x)=\lim _{x\to -\infty }ax+2+{\frac {4}{x}}=\lim _{x\to -\infty }ax=-\infty$

$\lim _{x\to 0^{+}}f_{a}(x)=0+2+{\frac {4}{0^{+}}}=+\infty$

$\lim _{x\to 0^{-}}f_{a}(x)=0+2+{\frac {4}{0^{-}}}=-\infty$

Si a est négatif, nous avons :

$\lim _{x\to +\infty }f_{a}(x)=\lim _{x\to +\infty }ax+2+{\frac {4}{x}}=\lim _{x\to +\infty }ax=-\infty$

$\lim _{x\to -\infty }f_{a}(x)=\lim _{x\to -\infty }ax+2+{\frac {4}{x}}=\lim _{x\to -\infty }ax=+\infty$

$\lim _{x\to 0^{+}}f_{a}(x)=0+2+{\frac {4}{0^{+}}}=+\infty$

$\lim _{x\to 0^{-}}f_{a}(x)=0+2+{\frac {4}{0^{-}}}=-\infty$

Si a est nul, nous avons :

$\lim _{x\to +\infty }f_{a}(x)=\lim _{x\to +\infty }2+{\frac {4}{x}}=2$

$\lim _{x\to -\infty }f_{a}(x)=\lim _{x\to -\infty }2+{\frac {4}{x}}=2$

$\lim _{x\to 0^{+}}f_{a}(x)=2+{\frac {4}{0^{+}}}=+\infty$

$\lim _{x\to 0^{-}}f_{a}(x)=2+{\frac {4}{0^{-}}}=-\infty$

Calculons la dérivée :

$f_{a}'(x)=a-{\frac {4}{x^{2}}}={\frac {ax^{2}-4}{x^{2}}}$

Si a est négatif ou nul, nous voyons que la dérivée est strictement négative et par conséquent la fonction est décroissante.

Si a est positif, la dérivée s'écrit alors :

$f_{a}'(x)={\frac {(x{\sqrt {a}}+2)(x{\sqrt {a}}-2)}{x^{2}}}$

Nous pouvons faire un tableau de signe :

${\begin{array}{c|ccccccc|}x&-\infty &&-{\frac {2}{\sqrt {a}}}&&0&&{\frac {2}{\sqrt {a}}}&&+\infty \\&&&\\\hline x{\sqrt {a}}-2&&-&&-&&-&0&+&\\\hline x{\sqrt {a}}+2&&-&0&+&&+&&+&\\\hline x^{2}&&+&&+&0&+&&+&\\\hline f_{a}'(x)&&+&0&-&\|&-&0&+&\\\hline \end{array}}$

Et nous en déduisons le sens de variation de la fonction f_a.

Un autre élément important est que pour toute valeur de a, nous voyons clairement que la droite d'équation y = ax + 2 est une asymptote car :

$\lim _{x\to \pm \infty }(f_{a}(x)-y)=\lim _{x\to \pm \infty }\left(ax+2+{\frac {4}{x}}-ax-2\right)=\lim _{x\to \pm \infty }{\frac {4}{x}}=0$

En résumé, nous voyons qu'il y a trois catégories de courbes :

La première catégorie de courbes correspond à des valeurs de a négatives donc le tableau de variation est :

Comme représentante de cette catégorie, nous avons choisi la fonction correspondant à a = -1, c'est-à-dire :

$f_{-1}(x)=-x+2+{\frac {4}{x}}$

La deuxième catégorie de courbes correspond à la valeur de a nulle donc le tableau de variation est :

Comme représentante de cette catégorie, nous avons choisi la fonction correspondant à a = 0, c'est-à-dire :

$f_{0}(x)=2+{\frac {4}{x}}$

La troisième catégorie de courbes correspond à des valeurs de a positives donc le tableau de variation est :

Comme représentante de cette catégorie, nous avons choisi la fonction correspondant à a = 1, c'est-à-dire :

$f_{1}(x)=x+2+{\frac {4}{x}}$

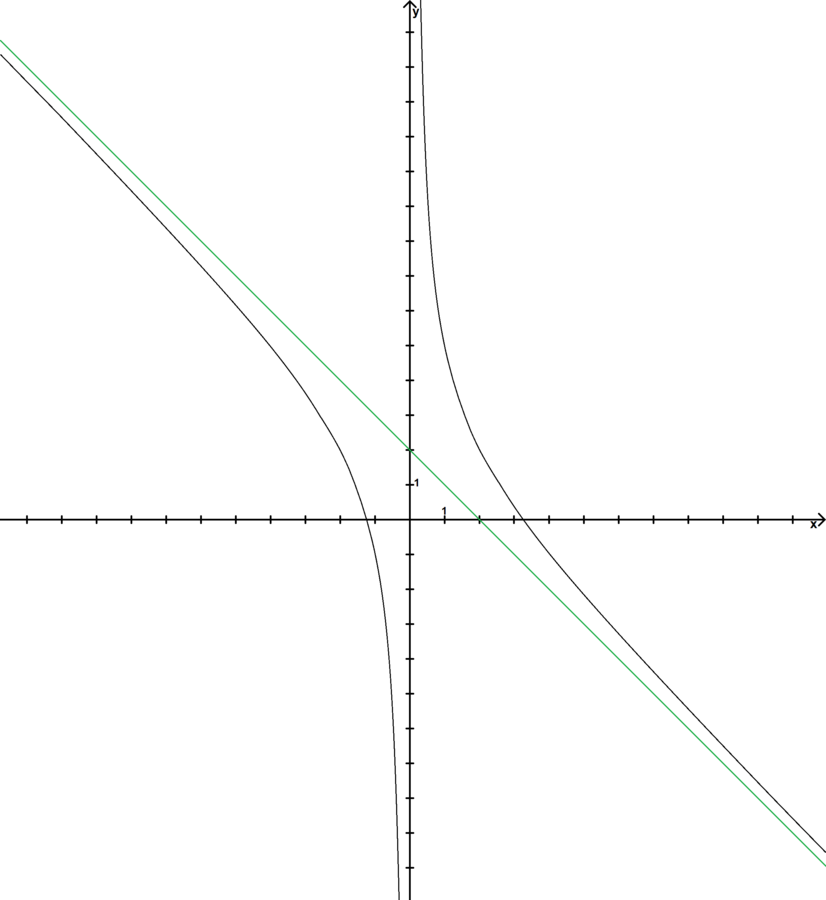
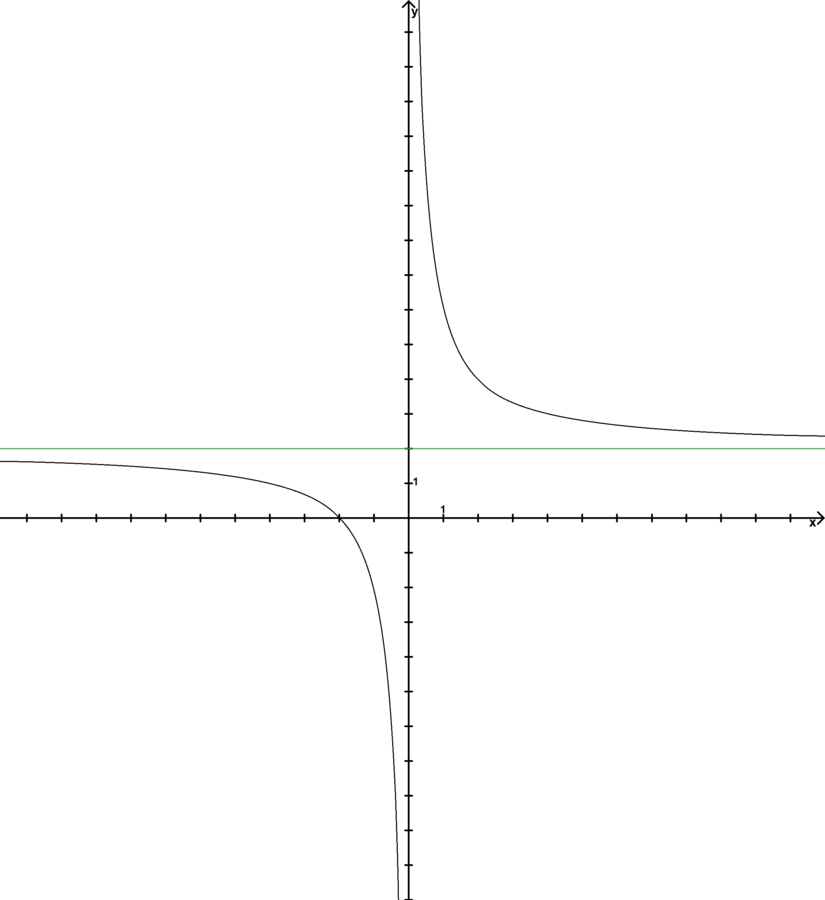
Les tracés des courbes correspondants seront respectivement :

• 
  Pour a négatif.
• 
  Pour a nul.
• 
  Pour a positif.

 

Exercice 9-4

1°  Soit M un point de coordonnées (a; b). Quelles sont les coordonnées d'un point M', image de M par la symétrie axiale par rapport à la droite d'équation y = x.

2°  En déduire, par un changement de repère, une relation que doit vérifier une fonction f pour que son tracé admette un axe de symétrie d'équation y = x + p.

3°  Calculer p de façon à ce que la droite d'équation y = x + p soit un axe de symétrie du tracé de la fonction f définie par :

$f(x)={\frac {5x-13}{x-3}}$

Solution

1°

Un vecteur directeur de la droite d'équation y = x est le vecteur ${\vec {w}}$ de coordonnées (1; 1).

Soit (u; v) les coordonnées de M'. Nous avons deux inconnues u et v, il nous faut donc deux équations contenant u et v.

La première équation sera obtenue en disant que les vecteurs ${\overrightarrow {MM'}}$ et ${\vec {w}}$ sont orthogonaux, c'est-à-dire que leur produit scalaire est nul. Ce qui se traduit par :

$1\times (u-a)+1\times (v-b)=0$

La deuxième équation sera obtenue en disant que le milieu du segment [MM'] est sur la droite d'équation y = x, ce qui s'écrit :

${\frac {b+v}{2}}={\frac {a+u}{2}}$

En simplifiant les équations précédentes, nous obtenons le système :

${\begin{cases}u-a+v-b=0\\b+v=a+u\end{cases}}$

dont la résolution donne :

${\begin{cases}u=b\\v=a\end{cases}}$

Le point symétrique de M de coordonnées (a; b) par rapport à la droite d'équation y = x est le point M' de coordonnées (b; a)

Autrement dit, pour trouver les coordonnées du symétrique d'un point par rapport à la droite d'équation y = x, il suffit d'inverser les coordonnées.

2°

Dans la question précédente, nous avons vu que prendre le symétrique d'un point par rapport à la droite Δ d'équation y = x revient à inverser les coordonnées. Par conséquent, pour étudier la symétrie par rapport à une droite d'équation y = x + p, nous pouvons simplifier le problème en nous ramenant à un repère où cette même droite aura pour équation Y = X. Pour cela, il suffit de poser comme relations de changement de repère :

${\begin{cases}X=x\\Y=x-p\end{cases}}$

Soit M, un point de coordonnées (a; b) dans l'ancien repère. Dans le nouveau repère, ses coordonnées seront (a; b-p). Les coordonnées de M' symétrique de M par rapport à Δ seront donc (b-p; a) dans le nouveau repère. Dans l'ancien repère, les coordonnées de M' seront finalement (b-p; a+p).

Si M appartient au tracé de la courbe f, nous pouvons écrire ses coordonnées sous la forme (x; f(x)). Le symétrique M' aura alors pour coordonnées (f(x)-p; x+p). Si le tracé de f admet Δ comme axe de symétrie, on en déduit que M' est aussi sur le tracé de f et par conséquent, on aura :

$x+p=f(f(x)-p)$

qui est la relation recherchée et que nous écrirons sous la forme :

$f\left(f(x)-p\right)-x-p=0$

Cette relation est suffisamment intéressante pour en faire un théorème que nous pouvons énoncer ainsi :

Début d’un théorème

Théorème

Le tracé d'une fonction f admet un axe de symétrie d'équation sous la forme y = x + p si et seulement si :

$\forall x\in \mathbb {R} \qquad f\left(f(x)-p\right)-x-p=0$

Fin du théorème

3°

Nous allons exposer deux méthodes pour résoudre cette question :

Première méthode

Nous allons écrire la relation obtenue à la question précédente et nous essayerons de déterminer une valeur de p qui rende cette relation vraie pour tout x.

On a :

$f\left(f(x)-p\right)-x-p=0$

en considérant l'expression de f(x), on obtient :

$f\left({\frac {5x-13}{x-3}}-p\right)-x-p=0$

Que l'on écrit :

$f\left({\frac {5x-13-px+3p}{x-3}}\right)-x-p=0$

En faisant de nouveau appel à l'expression de la fonction f, nous obtenons :

${\frac {5{\frac {5x-13-px+3p}{x-3}}-13}{{\frac {5x-13-px+3p}{x-3}}-3}}-x-p=0$

En simplifiant la fraction du premier membre et en faisant passer p et x dans le second membre :

${\frac {25x-65-5px+15p-13x+39}{5x-13-px+3p-3x+9}}=x+p$

En simplifiant et en effectuant le produit en croix :

$12x-26-5px+15p=(x+p)(2x-4-px+3p)$

En développant, en mettant tous les termes dans le premier membre et en réduisant les termes semblables :

$16x-26-10px+19p-2x^{2}+px^{2}+p^{2}x-3p^{2}=0$

Notre but est de trouver une valeur de p qui va rendre l'égalité précédente vraie pour tout x. Nous allons donc factoriser en fonction de x :

$(p-2)x^{2}+(p^{2}-10p+16)x-3p^{2}+19p-26=0$

qui donne en factorisant tous les facteurs du polynôme en x :

$(p-2)x^{2}+(p-2)(p-8)x-(p-2)(3p-13)=0$

qui se factorise finalement ainsi :

$(p-2)[x^{2}+(p-8)x-3p+13]=0$

Et nous voyons clairement que la valeur p = 2 va rendre la relation précédente vraie pour tout x.

On peut donc conclure que la droite d'équation y = x + 2 est axe de symétrie pour le tracé de la fonction f.

Deuxième méthode

Nous allons raisonner par conditions nécessaire et suffisante. C'est-à-dire que nous commencerons par essayer de trouver une condition nécessaire et nous vérifierons ensuite que cette condition est suffisante pour résoudre le problème.

Nous observons que le tracé de la courbe f a deux asymptotes. Une asymptote verticale d'équation x = 3 et une asymptote horizontale d'équation y = 5. Si le tracé de la courbe admet un axe de symétrie, alors nécessairement cet axe va passer par le point d'interception des asymptotes qui aura pour coordonnées (3; 5). Nous écrirons donc que les coordonnées du point d'interception des asymptotes vérifient l'équation y = x + p, soit :

$5=3+p$

et nous trouvons directement :

$p=2$

Ne nous emballons pas, ce n'est pas si simple. Ce que nous avons montré pour le moment, c'est que si nous avons un axe de symétrie d'équation y = x + p alors nécessairement p = 2. Mais nous n'avons pas encore prouvé que cette condition était suffisante. Rien ne dit pour le moment que la droite d'équation y = x + 2 est vraiment un axe de symétrie. Pour le prouver il nous faut vérifier la condition :

$\forall x\in \mathbb {R} \qquad f\left(f(x)-p\right)-x-p=0$

avec p = 2

Faisons donc ce calcul :

${\begin{aligned}\forall x\in \mathbb {R} \qquad f\left(f(x)-2\right)-2&=f\left({\frac {5x-13}{x-3}}-2\right)-x-2\\&=f\left({\frac {5x-13-2x+6}{x-3}}\right)-x-2\\&=f\left({\frac {3x-7}{x-3}}\right)-x-2\\&={\frac {5{\frac {3x-7}{x-3}}-13}{{\frac {3x-7}{x-3}}-3}}-x-2\\&={\frac {5(3x-7)-13(x-3)}{3x-7-3(x-3)}}-x-2\\&={\frac {2x+4}{2}}-x-2\\&=x+2-x-2\\&=0\end{aligned}}$

et là, nous pouvons conclure que la droite d'équation y = x + 2 est axe de symétrie de la courbe représentative de la fonction f.

 

Exercice 9-5

1°  Soit M, un point de coordonnées (a; b). Quelles sont les coordonnées d'un point M', image de M par la symétrie axiale par rapport à la droite d'équation y = -x.

2°  En déduire, par un changement de repère, une relation que doit vérifier une fonction f pour que son tracé admette un axe de symétrie d'équation y = -x + p.

3°  Calculer p de façon à ce que la droite d'équation y = -x + p soit un axe de symétrie du tracé de la fonction f définie par :

$f(x)={\frac {5x-13}{x-3}}$

Solution

1°

Un vecteur directeur de la droite d'équation y = -x est le vecteur ${\vec {w}}$ de coordonnées (1; -1).

Soit (u; v) les coordonnées de M'. Nous avons deux inconnues u et v, il nous faut donc deux équations contenant u et v.

La première équation sera obtenue en disant que les vecteurs ${\overrightarrow {MM'}}$ et ${\vec {w}}$ sont orthogonaux, c'est-à-dire que leur produit scalaire est nul. Ce qui se traduit par :

$1\times (u-a)-1\times (v-b)=0$

La deuxième équation sera obtenue en disant que le milieu du segment [MM'] est sur la droite d'équation y = -x, ce qui s'écrit :

${\frac {b+v}{2}}=-{\frac {a+u}{2}}$

En simplifiant les équations précédentes, nous obtenons le système :

${\begin{cases}u-a-v+b=0\\b+v=-a-u\end{cases}}$

dont la résolution donne :

${\begin{cases}u=-b\\v=-a\end{cases}}$

Le point symétrique de M de coordonnées (a; b) par rapport à la droite d'équation y = -x est le point M' de coordonnées (-b; -a)

Autrement dit, pour trouver les coordonnées du symétrique d'un point par rapport à la droite d'équation y = -x, il suffit d'inverser les coordonnées et de prendre leurs opposées.

2°

Dans la question précédente, nous avons vu que prendre le symétrique d'un point par rapport à la droite Δ d'équation y = -x revient à inverser les coordonnées et prendre leurs opposées. Par conséquent, pour étudier la symétrie par rapport à une droite d'équation y = -x + p, nous pouvons simplifier le problème en nous ramenant à un repère où cette même droite aura pour équation Y = -X. Pour cela, il suffit de poser comme relations de changement de repère :

${\begin{cases}X=x\\Y=x-p\end{cases}}$

Soit M, un point de coordonnées (a; b) dans l'ancien repère. Dans le nouveau repère, ses coordonnées seront (a; b-p). Les coordonnées de M' symétrique de M par rapport à Δ seront donc (-b+p; -a) dans le nouveau repère. Dans l'ancien repère, les coordonnées de M' seront finalement (-b+p; -a+p).

Si M appartient au tracé de la courbe f, nous pouvons écrire ses coordonnées sous la forme (x; f(x)). Le symétrique M' aura alors pour coordonnées (-f(x)+p; -x+p). Si le tracé de f admet Δ comme axe de symétrie, on en déduit que M' est aussi sur le tracé de f et par conséquent, on aura :

$-x+p=f(-f(x)+p)$

qui est la relation recherchée et que nous écrirons sous la forme :

$f\left(-f(x)+p\right)+x-p=0$

Cette relation est suffisamment intéressante pour en faire un théorème que nous pouvons énoncer ainsi :

Début d’un théorème

Théorème

Le tracé d'une fonction f admet un axe de symétrie d'équation sous la forme y = -x + p si et seulement si :

$\forall x\in \mathbb {R} \qquad f\left(-f(x)+p\right)+x-p=0$

Fin du théorème

3°

Nous allons exposer deux méthodes pour résoudre cette question :

Première méthode

Nous allons écrire la relation obtenue à la question précédente et nous essayerons de déterminer une valeur de p qui rende cette relation vraie pour tout x.

On a :

$f\left(-f(x)+p\right)+x-p=0$

en considérant l'expression de f(x), on obtient :

$f\left(-{\frac {5x-13}{x-3}}+p\right)+x-p=0$

Que l'on écrit :

$f\left({\frac {-5x+13+px-3p}{x-3}}\right)+x-p=0$

En faisant de nouveau appel à l'expression de la fonction f, nous obtenons :

${\frac {5{\frac {-5x+13+px-3p}{x-3}}-13}{{\frac {-5x+13+px-3p}{x-3}}-3}}+x-p=0$

En simplifiant la fraction du premier membre et en faisant passer p et x dans le second membre :

${\frac {-25x+65+5px-15p-13x+39}{-5x+13+px-3p-3x+9}}=p-x$

En simplifiant et en effectuant le produit en croix :

$-38x+104+5px-15p=(p-x)(-8x+22+px-3p)$

En développant, en mettant tous les termes dans le premier membre et en réduisant les termes semblables :

$-16x+104+10px-37p-8x^{2}+px^{2}-p^{2}x+3p^{2}=0$

Notre but est de trouver une valeur de p qui va rendre l'égalité précédente vraie pour tout x. Nous allons donc factoriser en fonction de x :

$(p-8)x^{2}-(p^{2}-10p+16)x+3p^{2}-37p+104=0$

qui donne en factorisant tous les facteurs du polynôme en x :

$(p-8)x^{2}-(p-2)(p-8)x+(p-8)(3p-13)=0$

qui se factorise finalement ainsi :

$(p-8)[x^{2}-(p-2)x+3p-13]=0$

Et nous voyons clairement que la valeur p = 8 va rendre la relation précédente vraie pour tout x.

On peut donc conclure que la droite d'équation y = -x + 8 est axe de symétrie pour le tracé de la fonction f.

Deuxième méthode

Nous allons raisonner par conditions nécessaire et suffisante. C'est-à-dire que nous commencerons par essayer de trouver une condition nécessaire et nous vérifierons ensuite que cette condition est suffisante pour résoudre le problème.

Nous observons que le tracé de la courbe f a deux asymptotes. Une asymptote verticale d'équation x = 3 et une asymptote horizontale d'équation y = 5. Si le tracé de la courbe admet un axe de symétrie, alors nécessairement cet axe va passer par le point d'interception des asymptotes qui aura pour coordonnées (3; 5). Nous écrirons donc que les coordonnées du point d'interception des asymptotes vérifient l'équation y = -x + p, soit :

$5=-3+p$

et nous trouvons directement :

$p=8$

Ne nous emballons pas, ce n'est pas si simple. Ce que nous avons montré pour le moment, c'est que si nous avons un axe de symétrie d'équation y = -x + p alors nécessairement p = 8. Mais nous n'avons pas encore prouvé que cette condition était suffisante. Rien ne dit pour le moment que la droite d'équation y = -x + 8 est vraiment un axe de symétrie. Pour le prouver il nous faut vérifier la condition :

$\forall x\in \mathbb {R} \qquad f\left(-f(x)+p\right)+x-p=0$

avec p = 8

Faisons donc ce calcul :

${\begin{aligned}\forall x\in \mathbb {R} \qquad f\left(-f(x)+8\right)+x-8&=f\left(-{\frac {5x-13}{x-3}}+8\right)+x-8\\&=f\left({\frac {-5x+13+8x-24}{x-3}}\right)+x-8\\&=f\left({\frac {3x-11}{x-3}}\right)+x-8\\&={\frac {5{\frac {3x-11}{x-3}}-13}{{\frac {3x-11}{x-3}}-3}}+x-8\\&={\frac {5(3x-11)-13(x-3)}{3x-11-3(x-3)}}+x-8\\&={\frac {2x-16}{-2}}+x-8\\&=-x+8+x-8\\&=0\end{aligned}}$

et là, nous pouvons conclure que la droite d'équation y = -x + 8 est axe de symétrie de la courbe représentative de la fonction f.

 

Exercice 9-6

Soit f une fonction dérivable sur un intervalle [a, b].

Supposons qu'il existe un réel M tel que :

• pour tout x de [a, b], f(x) ⩽ M
• il existe un réel x₀ dans ]a, b[ tel que f(x₀) = M.

Étudier la valeur f'(x₀).

Solution

f'(x₀) = 0 : voir théorème de Fermat sur les points stationnaires.

 

Exercice 9-7

On considère une fonction $f$ dérivable sur un intervalle $[a,b]$. On suppose en outre que $f(a)=f(b)=0$ et que $f_{d}'(a)>0$ et $f_{g}'(b)>0$ ($f_{d}'(a)$ désigne le nombre dérivé de $f$ à droite en $a$ et $f_{g}'(b)$ désigne le nombre dérivé de $f$ à gauche en $b$).

1. Prouver que $f$ prend des valeurs positives et négatives sur $]a,b[$.
2. En déduire que l'ensemble des éléments $x$ de $]a,b[$ tels que $f(x)=0$ est non vide.
3. Montrer que cet ensemble a un plus petit élément $c$.
4. Montrer que $f'(c)\leq 0$.
5. Conclure et interpréter graphiquement.

Solution

1. $\lim _{h\to 0^{+}}{\frac {f(a+h)}{h}}=f_{d}'(a)>0$ donc pour $h>0$ suffisamment petit, $f(a+h)>0$. De même, pour $h>0$ suffisamment petit, $f(b-h)<0$.
2. Théorème des valeurs intermédiaires.
3. D'après le point 1 ci-dessus, cet ensemble $E$ est inclus dans un intervalle $[a',b']$ tel que $a<a'<b'<b$. Sa borne inférieure $c$ appartient alors à $[a',b']$ et par continuité, $f(c)=0$. Donc $c\in E$.
4. $\forall x\in ]a,c[\quad f(x)\neq 0$ donc (d'après le point 1 ci-dessus) $f(x)>0$. Par conséquent, $f'(c)=f'_{g}(c)\leq 0$.
5. Au premier point après $a$ où $f$ s'annule, la tangente est à pente négative.