Théorie des graphes/Parcours
Parcourir un graphe permet de savoir si celui-ci est connexe ou non. Lorsque l’on parcourt un graphe, on part d'un sommet quelconque et on explore tous les autres sommets de proche en proche. Il existe deux types de parcours de graphe : en largeur et en profondeur.
Parcours en largeur
[modifier | modifier le wikicode]Ce type de parcours utilise une file pour déterminer si le graphe est connexe. Il fonctionne de la manière suivante :
- On met le nœud de départ dans la file ;
- On retire le nœud en tête de file afin d'examiner ses sommets adjacents ;
- On note le nœud que l’on examine ;
- On ajoute tous les voisins non examinés dans la file ;
- Si la file n’est pas vide, on reprend l'étape 2.
Si tous les nœuds ont été examinés à l'issu de l'algorithme, le graphe est connexe.
Exemple
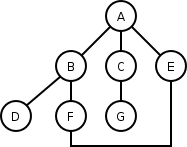
[modifier | modifier le wikicode]Dans ce cas, on parcourt le graphe dans l’ordre suivant : A, B, C, E, D, F, G.
Parcours en profondeur
[modifier | modifier le wikicode]Ce type de parcours utilise plutôt une pile pour déterminer si le graphe est connexe. Lorsque l’on parcourt le graphe, on part d'un sommet quelconque puis l’on explore à fond le premier chemin. Une fois le chemin fini ou lorsque l’on retombe sur un sommet déjà exploré, on recommence en partant du deuxième voisin. L'exemple indique plus en détail son fonctionnement.
Exemple
[modifier | modifier le wikicode]Si l’on reprend l'exemple précédent, on parcourt le graphe dans l’ordre suivant : A, B, D, F, E, C, G.