Introduction à la théorie des graphes/Définitions
Il est nécessaire, pour étudier la théorie des graphes, de se munir d'un crayon et d'un brouillon. En effet, pour comprendre la majorité des concepts, il sera plus qu'utile de faire un dessin.
Graphe[modifier | modifier le wikicode]
Un graphe est un objet mathématique particulier, nous devons donc commencer par le définir avant d’en étudier la théorie :
Un graphe G est un couple (V(G),E(G)) tel que V(G) est un ensemble non vide de sommets et E(G) un ensemble d'arêtes. Une arête de G étant une paire de sommets de G.
Pour simplifier, nous noterons V et E les ensembles V(G) et E(G).
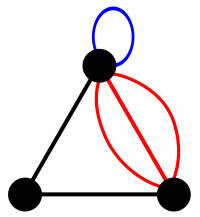
Pour mieux comprendre cette définition, voici un exemple :
Le graphe G peut être représenté par la figure ci-contre.
Notons que, d’après la définition, un graphe n'a pas une unique représentation graphique. La position des sommets et la forme des arêtes (une arête peut être courbe) n'ayant pas d'importance. Le choix de cette représentation s'appuie donc plus sur des critères esthétiques et de lisibilité.
Arêtes adjacentes, sommets voisins, arête incidente à un sommet[modifier | modifier le wikicode]
Voilà trois termes à ne pas confondre, voici leur définition :
Deux arêtes d'un graphe sont adjacentes si elles ont au moins un sommet en commun.
Dans un graphe, une arête est incidente à un sommet si .
Deux sommets d'un graphe sont voisins ou adjacents s'ils ont au moins une arête incidente en commun.
Ainsi, dans le graphe présenté dans l'exemple précédent, les arêtes e1 et e2 sont adjacentes car elles ont le sommet 1 en commun.
De même, nous pouvons dire qu'e1 est incidente au sommet 1, et que 1 et 2 sont voisins car ils sont reliés par l'arête e1.
Graphe simple[modifier | modifier le wikicode]
Lorsque plusieurs arêtes relient deux sommets, on les appelle des arêtes multiples.
Une boucle est une arête dont les deux extrémités sont identiques.
Un graphe est simple s'il ne contient ni boucle ni arêtes multiples.
Le graphe que nous avons étudié dans les exemples précédents était donc un graphe simple, mais ce n'est plus le cas du graphe représenté ci-contre.
En effet, en rouge nous pouvons observer des arêtes multiples, et en bleu une boucle.
Un graphe qui n’est pas simple est aussi appelé multigraphe.
Degré d'un sommet[modifier | modifier le wikicode]
Dans un graphe, le degré d'un sommet v, noté d(v), correspond au nombre d'arêtes incidentes à v.
Par convention, une boucle, touchant deux fois le sommet, sera comptée comme deux arêtes incidentes.
Cette définition nous permet maintenant d'introduire notre premier théorème :
Dans un graphe simple,
Dans un graphe simple, chaque arête relie deux sommets. Donc, quand on fait la somme des degrés, chaque arête est comptée deux fois : une fois dans le degré de sa première extrémité et une fois dans le degré de la seconde.
Il existe d'autres démonstrations pour ce théorème qui sont sans doute plus formelles. Cependant, nous n'avons pas encore les outils pour les étudier.
Dans un graphe simple, le nombre de sommets de degré impair est pair.
D'après le théorème précédent, nous avons :
Notons
Donc est pair.
On en déduit que le nombre de sommets de degré impair () est pair.
Quelques graphes particuliers[modifier | modifier le wikicode]
Graphe régulier[modifier | modifier le wikicode]
Un graphe est dit k-régulier si tous ses sommets sont de degré k.
-
graphe 0-régulier -
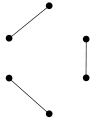
graphe 1-régulier -
graphe 2-régulier -
graphe de Petersen 3-régulier
Graphe complet[modifier | modifier le wikicode]
Un graphe complet à n sommets, noté , est le graphe simple dont tous les sommets sont reliés deux à deux.
- Un graphe complet à n sommets :
- est (n-1)-régulier.
- possède arêtes.
