Introduction à la cristallographie/Empilements compacts

**Empilements compacts**
Leçon : Introduction à la cristallographie

Chapitre n^o 3
Chap. préc. :	Systèmes cristallins
Chap. suiv. :	Types de cristaux

En raison de limitations techniques, la typographie souhaitable du titre, « Introduction à la cristallographie : Empilements compacts
Introduction à la cristallographie/Empilements compacts », n'a pu être restituée correctement ci-dessus.

À partir de ce chapitre, on fait l'hypothèse que les constituants du cristal (ions, atomes, molécules…) se comportent comme des « sphères dures »^[1]. La question qui se pose est : quel est le meilleur moyen d'empiler de telles sphères ?

En d'autres termes, comment les disposer de sorte à en placer un maximum, dans un espace minimum ?

Empilement compact

La solution, conjecturée en 1611 par Johannes Kepler, posée en 1900 comme l'un des « problèmes du Millénium » par David Hilbert, ne fut complètement démontrée qu'en 1999 — c’est dire à quel point le sujet est complexe.

En voici une description simple :

on place trois sphères pour former un triangle équilatéral ;
on pose une quatrième sphère sur le creux formé par les précédentes ;
on recommence ainsi jusqu'à paver l'espace.

Il existe, en fait, deux manières de réaliser un tel empilement. Supposons un plan pavé de sphères, notons le A. On peut, en plaçant des sphères dans les creux, créer une nouvelle couche, notée B. Une troisième couche peut être formée :

soit en posant des sphères au dessus des sphères de A — on parle d'empilement AB ou ABA ;
soit en posant des sphères décalées par rapport à celles de A et B — on parle d'empilement ABC.

Respectivement, on parle :

d'empilement hexagonal compact ;
d'empilement cubique à faces centrées.

En prenant le modèle des « sphères dures », un empilement compact se caractérise par une compacité maximale, égale à :

$c_{\rm {max}}={\frac {\pi }{3{\sqrt {2}}}}\approx 74\%$

La compacité étant le rapport du volume occupé par les sphères d'une maille sur le volume de la maille elle-même.

Étude de l'empilement compact à faces centrées

Maille de l'empilement cubique à faces centrées.

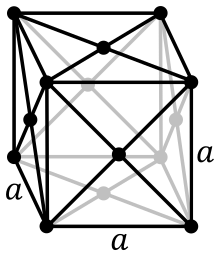
L'empilement cubique à faces centrées (cfc) est caractérisé par les nœuds de son réseau qui sont situés :

aux 8 sommets d'un cube ;
au centre des faces de ce cube.

La maille possède 14 nœuds, mais certains de ces nœuds sont partagés avec les mailles voisines : les huit sommets sont partagés chacun avec huit mailles, les 6 nœuds au centre des faces sont partagés entre deux mailles. Le nombre de nœuds propres à la maille est donc :

$n={\frac {1}{8}}8+{\frac {1}{2}}6=1+3=4$

Plus concrètement, cela veut dire que 4 atomes appartiennent en propre à la maille (si on ne considère que ce qu’il y a à l'intérieur du cube formé par la maille, nous avons 4 atomes).

Notons r le rayon des atomes constituants le cristal étudié. On peut alors chercher la paramètre de maille a, c'est-à-dire le côté du cube. En effet, puisque les sphères ne s'interpénètrent pas, sur une face, trois atomes sont mitoyens : sur une diagonale, on a :

la moitié de l'atome du sommet ;
l'atome au centre ;
la moitié de l'atome à l'autre sommet.

Un cristal cubique à face centrée : la halite (sel de table, NaCl).

Ainsi, la diagonale de la face est de longueur : $r+2r+r=4r$ . D'un autre côté, elle est de longueur $a{\sqrt {2}}$ comme diagonale d'un carré de côté a. Par conséquent, la maille est de côté :

$a=2{\sqrt {2}}\ r,$

Calculons maintenant la compacité de ce cristal :

Volume de la maille : $V_{\rm {maille}}=a^{3}=r^{3}16{\sqrt {2}}$ ;
Volume occupé par les atomes : $V_{\rm {atomes}}=n{\frac {4}{3}}\pi r^{3}=r^{3}{\frac {16}{3}}\pi$
$n$ étant le nombre d'atomes appartenant en propre à la maille et ${\frac {4}{3}}\pi r^{3}$ étant le volume de la sphère de rayon $r$ , autrement dit le volume d'un atome.

La compacité est le rapport de la seconde sur la première, soit :

${\begin{aligned}c_{\rm {cfc}}&={\frac {V_{\rm {atomes}}}{V_{\rm {maille}}}}\\\ &={\frac {r^{3}{\frac {16}{3}}\pi }{r^{3}16{\sqrt {2}}}}\\\ &={\frac {\pi }{3{\sqrt {2}}}}\\\ &=c_{\rm {max}}\end{aligned}}$

C'est donc un empilement compact. Un exemple d'assemblage cubique à faces centrées est le cristal de halite, ou sel de table, où les anions chlorure occupent les nœuds de la maille (et les cations sodium occupent les sites octaédriques).

Notons M la masse molaire moléculaire des atomes constituant le cristal. On note N_A la constante d'Avogadro ( $N_{A}\approx 6,022\times 10^{23}mol^{-1}$ ). Alors la masse d'une maille est :

$m_{\rm {maille}}=n(M/N_{A})=4(M/N_{A})$

La masse volumique du cristal est alors :

$\rho _{\rm {cfc}}={\frac {m_{\rm {maille}}}{V_{\rm {maille}}}}={\frac {4M}{N_{A}r^{3}16{\sqrt {2}}}}={\frac {M}{N_{A}r^{3}4{\sqrt {2}}}}$

En connaissant le rayon d'un atome et sa masse molaire, on peut en déduire la masse volumique du cristal.

Puis en déduire sa densité, en effectuant le quotient de sa masse volumique et de celle de l'eau.

La coordinence de cet assemblage, c'est-à-dire le nombre de ses plus proches voisins, s'élève à 12. En effet, partant d'un nœud au centre d'une face, il y a : 4 atomes voisins dans la maille, 4 atomes voisins dans la face (les sommets) et 4 atomes voisins dans la maille voisine.

Sites interstitiels de l'assemblage cubique à faces centrées

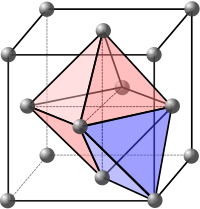
Comme on peut l'observer, il existe des espaces « vides » entre ces sphères, bien que l'empilement soit « compact ». En théorie comme en pratique, on peut y placer des atomes (ions, molécules…) plus petits. On distingue, pour l'essentiel, deux genres de sites intersticiels : les sites tétraédriques et les sites octaédriques. Nous nous attachons ici au cas de l'empilement compact cubique à faces centrées. Nous désignerons le côté de la maille par a.

Sites tétraédriques

Les sites tétraédriques sont définis comme suit : il s'agit du centre d'un octant — un octant étant l'un des huit cubes d'arêtes a/2 partageant un sommet de la maille. On observe que les atomes de l'octant forment un tétraède (d'où le nom « tétraédrique »). On a, ainsi, au maximum, 8 sites tétraédriques — cela est souvent source d'erreurs.

Un point important est que les sites tétraédriques sont dans la maille, c'est-à-dire qu’ils ne sont pas partagés par les mailles voisines.

Sites octaédriques

Les sites octaédriques sont définis comme suit : ils sont au centre des octaèdres formés par les atomes de la mailles (d'où le nom « octaédrique »). Notamment, il y en a un au centre de la maille, et il y en a 12 autres au milieu des arêtes (il ne faut pas oublier que la maille est répétée dans les trois dimensions de l'espace) qui sont partagées avec 4 mailles chacun. Il a donc, pour une maille, au maximum :

$1+12/4=1+3=4$ sites octaédriques.

Étude de l'empilement hexagonal compact

Un cristal à structure hexagonale compacte : le béryl.

L'empilement hexagonal compact (hc) est l'autre assemblage compact. La maille que l’on étudie dans ce cas est un prisme droit à base losange (1/3 de la maille hexagonale) appelé « maille conventionnelle ». On appelle « triangle équilatéral » chaque moitié de la base losange. Cette maille se caractérise par la présence de :

8 nœuds, coïncidant avec les sommets du prisme ;
1 nœud « central » situé à mi-hauteur et sous le centre de gravité d'un des triangles équilatéraux.

La maille conventionnelle possède 9 nœuds, dont les huit premiers sont partagés avec 8 mailles voisines, elle possède donc :

$n={\frac {1}{8}}8+1=2$ nœuds propres.

L'atome central forme avec le triangle équilatéral sous-jacent un tétraèdre régulier (figure 2). Nous allons utiliser les relations de géométrie relativement simple pour en déduire un lien entre le côté de la base losange, noté a, et la hauteur de la maille, notée c. On note r le rayon d'un atome du cristal, alors en particulier a = 2r.

Le centre de gravité du triangle équilatéral est situé aux 2/3 de l'une de ses médianes : $2m/3$ ;
On connait un coté du tétraèdre : il est de longueur a.

Reste à déterminer la longueur d'une médiane :

Par le théorème de Pythagore, $a^{2}=m^{2}+a^{2}/4$ d'où $m^{2}=a^{2}(1-1/4)$ . On a donc : $m=a{\sqrt {\frac {3}{4}}}$

Utilisons maintenant le théorème de Pythagore dans le tétraèdre pour obtenir sa hauteur :

$h^{2}=a^{2}-(2m/3)^{2}=a^{2}-{\frac {4}{9}}a^{2}{\frac {3}{4}}=a^{2}\left(1-{\frac {1}{3}}\right)=a^{2}{\frac {2}{3}}$

On a ainsi la hauteur de la maille, égale à 2h :

$c=2h=2a{\sqrt {\frac {2}{3}}}$

Le volume de la maille est égale à l'aire de la base multipliée par la hauteur de la maille :

$V_{\rm {maille}}=cma=2a{\sqrt {\frac {2}{3}}}a{\sqrt {\frac {3}{4}}}a=a^{3}{\sqrt {2}}=r^{3}8{\sqrt {2}}$

Le volume occupé par un atome est, quant à lui :

$V_{\rm {atome}}={\frac {4}{3}}\pi r^{3}$

La compacité est ainsi :

${\begin{aligned}c_{\rm {hc}}&={\frac {nV_{\rm {atome}}}{V_{\rm {maille}}}}\\\ &={\frac {2{\frac {4}{3}}\pi r^{3}}{r^{3}8{\sqrt {2}}}}\\\ &={\frac {\pi }{3{\sqrt {2}}}}\\\ &=c_{\rm {max}}\end{aligned}}$

Il s'agit bien d'un assemblage compact. Notons M la masse molaire des atomes constituant le cristal, et N_A la constante d'Avogadro. Alors la masse de la maille est :

$m_{\rm {maille}}=nM/N_{A}=2M/N_{A}$

La masse volumique du cristal est alors :

$\rho _{\rm {hc}}={\frac {m_{\rm {maille}}}{V_{\rm {maille}}}}={\frac {2M}{N_{A}}}{\frac {1}{r^{3}8{\sqrt {2}}}}={\frac {M}{4N_{A}r^{3}{\sqrt {2}}}}$

On peut remarquer que cette densité est identique à celle de l'assemblage cubique à faces centrées — cela est lié à leur compacité, maximale.

La coordinence d'un tel assemblage est de 12 : 6 atomes dans le même plan, 3 dans le plan au-dessus, 3 dans le plan au-dessous.

Sites interstitiels de l'empilement hexagonal compact

Pour étudier les sites interstitiels de cet empilement, il faut revenir à la maille hexagonale complète. On retrouve :

12 sites tétraédriques, au centre de chacun des 12 tétraèdres formant la maille (soit 4 par maille conventionnelle) ;
6 sites octaédriques par maille (soit 2 par maille conventionnelle).

En particulier, il existe une symétrie haut-bas dans l'emplacement de ces sites. On pourra les observer ici : « Structure « hexagonal compact » ».

Remarques

↑ Il s'agit de sphères, et pas de boules — cela est lié au fait que les dimensions d'un atome sont gigantesques devant celles de son noyau : une telle sphère est pratiquement vide.

Introduction à la cristallographie

Systèmes cristallins

Types de cristaux

[1] Il s'agit de sphères, et pas de boules — cela est lié au fait que les dimensions d'un atome sont gigantesques devant celles de son noyau : une telle sphère est pratiquement vide.

[1]