Une page de Wikiversité, la communauté pédagogique libre.
En raison de limitations techniques, la typographie souhaitable du titre, «
Annexe : Fonction racine carréeÉtude et tracé d'une fonction/Annexe/Fonction racine carrée », n'a pu être restituée correctement ci-dessus.
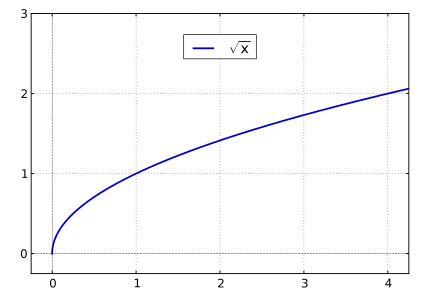
Représentation graphique de la fonction racine carrée.
R
{\displaystyle \mathbb {R} }
[
0
,
+
∞
[
{\displaystyle \left[0,+\infty \right[}
R
{\displaystyle \mathbb {R} }
C
{\displaystyle \mathbb {C} }
Fonction racine carrée réelle
Propriété
La fonction dérivée de la fonction racine carrée est donnée par :
d
d
x
x
:
]
0
,
+
∞
[
→
R
,
x
↦
1
2
x
{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}{\sqrt {x}}:\left]0,+\infty \right[\to \mathbb {R} ,\;x\mapsto {1 \over 2{\sqrt {x}}}}
'Démonstration'
Notons
f
:
R
+
→
R
{\displaystyle f:\mathbb {R} _{+}\to \mathbb {R} }
Si
a
>
0
{\displaystyle a>0}
h
≥
−
a
{\displaystyle h\geq -a}
h
≠
0
{\displaystyle h\neq 0}
f
(
a
+
h
)
−
f
(
a
)
h
=
a
+
h
−
a
h
=
(
a
+
h
−
a
)
(
a
+
h
+
a
)
h
(
a
+
h
+
a
)
=
a
+
h
−
a
h
(
a
+
h
+
a
)
=
h
h
(
a
+
h
+
a
)
=
1
a
+
h
+
a
{\displaystyle {\frac {f(a+h)-f(a)}{h}}={\frac {{\sqrt {a+h}}-{\sqrt {a}}}{h}}={\frac {({\sqrt {a+h}}-{\sqrt {a}})({\sqrt {a+h}}+{\sqrt {a}})}{h({\sqrt {a+h}}+{\sqrt {a}})}}={\frac {a+h-a}{h({\sqrt {a+h}}+{\sqrt {a}})}}={\frac {h}{h({\sqrt {a+h}}+{\sqrt {a}})}}={\frac {1}{{\sqrt {a+h}}+{\sqrt {a}}}}}
.
On obtient alors
lim
h
→
0
f
(
a
+
h
)
−
f
(
a
)
h
=
1
a
+
0
+
a
=
1
2
a
{\displaystyle \lim _{h\to 0}{\frac {f(a+h)-f(a)}{h}}={\frac {1}{{\sqrt {a+0}}+{\sqrt {a}}}}={\frac {1}{2{\sqrt {a}}}}}
a
{\displaystyle a}
Si
a
=
0
{\displaystyle a=0}
alors, pour tout
h
>
0
{\displaystyle h>0}
, on a
f
(
a
+
h
)
−
f
(
a
)
h
=
h
h
=
1
h
{\displaystyle {\frac {f(a+h)-f(a)}{h}}={\frac {\sqrt {h}}{h}}={\frac {1}{\sqrt {h}}}}
et
lim
h
→
0
+
1
h
=
+
∞
{\displaystyle \lim _{h\to 0^{+}}{\frac {1}{\sqrt {h}}}=+\infty }
. Donc
f
{\displaystyle f}
n’est pas dérivable en
0
{\displaystyle 0}
.
Corollaire
La fonction racine carrée est strictement croissante sur son ensemble de définition.
Représentation graphique de la fonction racine carrée (en vert) et de sa dérivée (en rouge).
Propriété
Pour tous réels
y
≥
x
≥
0
{\displaystyle y\geq x\geq 0}
0
≤
y
−
x
≤
y
−
x
{\displaystyle 0\leq {\sqrt {y}}-{\sqrt {x}}\leq {\sqrt {y-x}}}
(Pour cette raison, la fonction racine carrée est dite «
1
2
{\displaystyle {\tfrac {1}{2}}}
'Démonstration'
Pour tous réels
y
≥
x
≥
0
{\displaystyle y\geq x\geq 0}
x
≤
y
≤
x
+
y
−
x
car
x
≤
y
≤
x
+
2
x
(
y
−
x
)
+
y
−
x
{\displaystyle {\sqrt {x}}\leq {\sqrt {y}}\leq {\sqrt {x}}+{\sqrt {y-x}}\quad {\text{car }}x\leq y\leq x+2{\sqrt {x(y-x)}}+y-x}
== Référents [Modifier ==
Ces personnes sont prêtes à vous aider concernant cette leçon :










![{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}{\sqrt {x}}:\left]0,+\infty \right[\to \mathbb {R} ,\;x\mapsto {1 \over 2{\sqrt {x}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6ccb6507af5b885606c530088ecbe7392fadb67c)
















