Cinématique des fluides/Définitions
Variables d'Euler
[modifier | modifier le wikicode]Les variables d'Euler rassemblent toutes les grandeurs de champ susceptibles de décrire le déplacement du fluide ou les modifications de ses propriétés :
- masse volumique ,
- vitesse ,
- quantité de mouvement ,
- température ,
- pression ,
- concentration des différentes espèces chimiques,
- etc.
Quantité de mouvement
[modifier | modifier le wikicode]En mécanique de point, la quantité de mouvement d'un point matériel de masse animé d'une vitesse est définie comme produit de la masse et de la vitesse : . Elle fait partie des grandeurs qui se conservent, comme l’énergie et la masse.
Soit la quantité de mouvement d'une particule de fluide de volume et de masse .
Soit la quantité de mouvement d'un fluide de volume V.
La quantité de mouvement s'exprime aussi en fonction de la masse et de l'accélération :
- .
Ligne et tube de courant
[modifier | modifier le wikicode]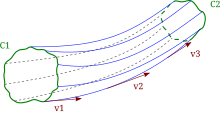
Une ligne de courant est une courbe tangente aux vecteurs vitesse à un instant donné.
Une surface de courant est une surface constituée de lignes de courant adjacentes. Il n'y a donc pas de fluide qui traverse cette surface puisqu'elle est orientée en tout point dans la direction de l'écoulement.
Un tube de courant est une surface de courant qui s'appuie sur une courbe fermée. Le flux est donc le même en n'importe quelle section du tube.
On appelle tube de courant toute surface formée uniquement de lignes de courant, et il n'y a donc pas de flux traversant ce tube puisque ses parois sont orientées dans la direction de l'écoulement.
Débits
[modifier | modifier le wikicode]Débit volumique
[modifier | modifier le wikicode]Le débit volumique, exprimé en m3·s−1 dans le Système international d'unités, est le volume de fluide qui s'écoule à travers une surface par unité de temps. Il permet de quantifier le flux en termes de volume. Par exemple, dans le cas d'un tube, on imagine une surface perpendiculaire à l'axe du tube, appelée section, et on compte, pendant une seconde, combien de mètres cubes sont passés à travers.
- où est le volume de fluide ayant traversée la section durant le temps ; est le débit volumique moyen pendant la durée .
De façon similaire, on définit le débit volumique instantané tel que .
Le débit volumique traversant un élément de surface orienté , de vecteur normal unitaire , a un débit volumique élémentaire qui peut s'écrire :
- .
Le débit volumique instantané traversant une surface :
- .
Le débit volumique peut être négatif puisque le produit scalaire entre le vecteur du déplacement du volume et le vecteur normal à la surface peut être négatif.
Si le vecteur de déplacement du volume est le même sur toute la surface, elle-même perpendiculaire à la direction de l'écoulement, alors le débit volumique est égal au produit de la vitesse et de la section S :
- .
Débit massique
[modifier | modifier le wikicode]Le débit massique, exprimé en kg·s−1 dans le Système international d'unités, quantifie la masse de fluide qui s'écoule à travers une surface fictive par unité de temps. Par exemple, on se place au bout d'un tube et on mesure la masse de fluide qui s'est écoulée en une seconde : c’est le débit massique.
- où est la masse de fluide ayant traversée la section droite durant le temps ; est le débit moyen pendant la durée .
Débit volumique et débit massique sont liés entre eux par l'intermédiaire de la masse volumique du fluide considéré :
- .
De façon similaire, on définit le débit massique instantané . Le flux traversant un élément de surface orienté , de vecteur normal unitaire , a un débit élémentaire qui peut s'écrire :
- .
Le débit massique instantané traversant une surface S :
- .
Enfin, si le vecteur déplacement est le même sur toute la surface, et perpendiculaire à celle-ci, le débit massique s'exprime :
- .






































