En raison de limitations techniques, la typographie souhaitable du titre, «
Exercice : Matrice de passage, vecteur déplacement
Cinématique (Expert)/Exercices/Matrice de passage, vecteur déplacement », n'a pu être restituée correctement ci-dessus.
Soit un repère  à positionner par rapport à un repère
à positionner par rapport à un repère  .
.
Nous définissions le vecteur nodal  perpendiculaire au plan défini par les vecteurs
perpendiculaire au plan défini par les vecteurs  et
et  , d'où
, d'où 
Une première rotation d'angle  (psi) mesuré positivement autour de
(psi) mesuré positivement autour de  , nommé précession, permet de passer du repère
, nommé précession, permet de passer du repère  au repère
au repère  .
.
Une rotation d'angle  (theta) mesuré positivement autour de
(theta) mesuré positivement autour de  , appelée nutation, permet de passer du repère
, appelée nutation, permet de passer du repère  au repère
au repère  .
.
Enfin, une rotation d'angle  (phi) mesuré positivement autour de
(phi) mesuré positivement autour de  , la rotation propre, permet d'atteindre le repère
, la rotation propre, permet d'atteindre le repère 
Déterminer les matrices de passage de chaque rotation élémentaire.
Solution

 →
→  angle de précession
angle de précession
 →
→  angle de nutation
angle de nutation
 →
→  angle de rotation propre
angle de rotation propre
- Solution pour
 angle de précession :
angle de précession : ![{\displaystyle \mathbb {P} _{[R_{0}\rightarrow R_{1}]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ff74ea6f75170908a8728d1a08d7e0a8d05aa23)
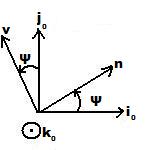
La matrice de passage associé à cette rotation est : 
![{\displaystyle \mathbb {P} _{[R_{0}\rightarrow R_{1}]}={\begin{bmatrix}cos\psi &-sin\psi &0\\sin\psi &cos\psi &0\\0&0&1\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b62ccee84332b5796505f89f1158a6a59f36d09)
 sont les vecteurs unitaires respectif de
sont les vecteurs unitaires respectif de 
- Solution pour
 angle de nutation :
angle de nutation : ![{\displaystyle \mathbb {P} _{[R_{1}\rightarrow R_{2}]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d76503b6c418ed939286ccd67ff2bfddf51fd325)
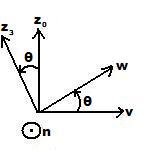
La matrice de passage associé à cette rotation est : ![{\displaystyle \mathbb {P} _{[R_{1}\rightarrow R_{2}]}={\begin{bmatrix}1&0&0\\0&cos\theta &-sin\theta \\0&sin\theta &cos\theta \end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a40041fcd0e9fe3461452ee8aec4d85daa340385)
- Solution pour
 angle de rotation propre :
angle de rotation propre : ![{\displaystyle \mathbb {P} _{[R_{2}\rightarrow R_{3}]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c7140d35d31c16976d263b52901620942d11c4c8)
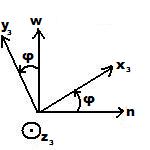
La matrice de passage associé à cette rotation est : ![{\displaystyle \mathbb {P} _{[R_{2}\rightarrow R_{3}]}={\begin{bmatrix}cos\varphi &-sin\varphi &0\\sin\varphi &cos\varphi &0\\0&0&1\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f9f37e65c86289fdcf5ec3231e7ab4854375722)
Déterminer la matrice de passage (générale).
Solution
Cette solution n'a pas été rédigée. Vous pouvez le faire en modifiant le paramètre « contenu » du modèle. Comment faire ?
En utilisant les résultats obtenus au cours de l'activité 2, déterminer la matrice de inverse.  est-elle une matice rotation ?
est-elle une matice rotation ?
Solution
Cette solution n'a pas été rédigée. Vous pouvez le faire en modifiant le paramètre « contenu » du modèle. Comment faire ?
On associe au solide 0 un repère. Le solide 0 est considéré comme solide de référence.
Un solide 3 muni d'un repère  se déplace dans l'espace par rapport au solide de référence.
se déplace dans l'espace par rapport au solide de référence.
À l'instant initial de l'étude  , les deux repères
, les deux repères  et
et  sont coïncidents.
sont coïncidents.
On considère un point A appartenant au solide 3 tel que :

Le solide se déplace d'une translation tel qu’à l'instant  :
: 
Il subit une rotation propre autour de l’axe  caractérisée par
caractérisée par  . À l'instant
. À l'instant  .
.
Déterminer le vecteur déplacement  .
.
Solution
Cette solution n'a pas été rédigée. Vous pouvez le faire en modifiant le paramètre « contenu » du modèle. Comment faire ?
Nous observons un déplacement tel que qu’à l'instant  :
: 
Il subit trois rotations telles qu’à l'instant  :
: 
Déterminer le vecteur déplacement  .
.
Solution
Cette solution n'a pas été rédigée. Vous pouvez le faire en modifiant le paramètre « contenu » du modèle. Comment faire ?















![{\displaystyle \mathbb {P} _{[R_{0}\rightarrow R_{1}]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ff74ea6f75170908a8728d1a08d7e0a8d05aa23)

![{\displaystyle \mathbb {P} _{[R_{0}\rightarrow R_{1}]}={\begin{bmatrix}cos\psi &-sin\psi &0\\sin\psi &cos\psi &0\\0&0&1\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b62ccee84332b5796505f89f1158a6a59f36d09)


![{\displaystyle \mathbb {P} _{[R_{1}\rightarrow R_{2}]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d76503b6c418ed939286ccd67ff2bfddf51fd325)

![{\displaystyle \mathbb {P} _{[R_{1}\rightarrow R_{2}]}={\begin{bmatrix}1&0&0\\0&cos\theta &-sin\theta \\0&sin\theta &cos\theta \end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a40041fcd0e9fe3461452ee8aec4d85daa340385)
![{\displaystyle \mathbb {P} _{[R_{2}\rightarrow R_{3}]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c7140d35d31c16976d263b52901620942d11c4c8)

![{\displaystyle \mathbb {P} _{[R_{2}\rightarrow R_{3}]}={\begin{bmatrix}cos\varphi &-sin\varphi &0\\sin\varphi &cos\varphi &0\\0&0&1\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f9f37e65c86289fdcf5ec3231e7ab4854375722)










