Évolution temporelle des systèmes mécaniques/Mouvement des planètes et des satellites

Début de la boite de navigation du chapitre

fin de la boite de navigation du chapitre

Le système solaire

Planètes et satellites

Ces objets sont en mouvement grâce à la force de gravitation universelle.

Loi d'attraction universelle (rappels)

Corps ponctuels

On considère deux objets :

• un objet de masse m_A placé en A
• un objet de masse m_B placé en B

Comme ces corps ont une masse, ils exercent l'un sur l'autre une force, d'expression :

${\overrightarrow {F}}_{A\rightarrow B}=-G{\frac {m_{A}m_{B}}{AB^{2}}}\times {\overrightarrow {u}}_{AB}$

On peut supposer qu'un corps est ponctuel si on peut identifier le corps à son centre de gravité en lequel est placée toute la masse du corps. On ne prend ainsi en compte que certains phénomènes pour simplifier une étude. Par exemple, supposer la Terre comme un corps ponctuel dans son mouvement autour du Soleil néglige la rotation de la Terre sur elle-même, ainsi que le fait que la force d'attraction exercée par le Soleil n’est pas égale en tout point de la Terre.

Objets à répartition sphérique de masse

Si les deux objets sont deux sphères homogènes, de centres de gravité respectifs A et B, alors la force exercée par le corps en A sur le corps en B s'applique en B et vaut :

${\vec {F}}_{A/B}=-{\vec {F}}_{B/A}=-G{\frac {m_{A}m_{B}}{AB^{2}}}{\vec {u}}_{AB}$

Référentiel héliocentrique

Le repère $(S,{\vec {i}},{\vec {j}},{\vec {k}})$ attaché au référentiel héliocentrique, est défini par le centre S du Soleil, et 3 axes dont les directions données par 3 étoiles lointaines considérées comme fixes E₁, E₂ et E₃.

Référentiel géocentrique

Ne pas confondre avec référentiel terrestre !!

Utilisé pour décrire les mouvements des satellites terrestres,le référentiel géocentrique a pour origine le centre de gravité terrestre, et ses axes sont définis par rapport à des étoiles. Ainsi, il n’est pas solidaire de la Terre dans son mouvement de rotation autour des pôles, et ce référentiel peut être considéré comme galiléen sur des expériences terrestres "peu longues" (une journée maximum), car la rotation de la Terre autour du Soleil n'est alors pas prise en compte. Ce reférentiel est un solide imaginaire constitué de la terre et d'étoiles suffisamment lointaines pour sembler immobiles

Les lois de Kepler

Les deux premières lois de Kepler (1609)

1^e loi : loi des orbites

Dans un référentiel héliocentrique, les planètes décrivent des ellipses dont le centre du Soleil S est l'un des foyers. Les orbites sont planes. Le cercle est une orbite elliptique particulière dont S est le centre.

2^e loi : loi des aires

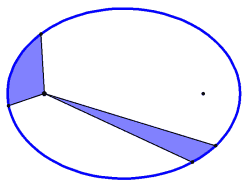
Pendant une durée donnée $\Delta t$, le rayon qui joint le centre S du Soleil au centre d'une planète balaie une aire $\Delta {\mathcal {A}}$ constante, quelle que soit la position de la planète sur son orbite. Le rapport ${\frac {\Delta {\mathcal {A}}}{\Delta t}}$ est constant pour une planète donnée.

3^e loi de Kepler (1619)

3^e loi : loi des périodes

Le carré de la durée d'une révolution $T$ d'une planète est proportionnel au cube de la longueur du demi grand axe de l'ellipse $a$.

Application en formule

${\frac {T^{2}}{a^{3}}}=K_{s}$, avec $K_{s}$ la constante qui dépend du système attracteur.

Satellite d'une planète

Les 3 lois de Kepler s'appliquent également aux satellites d'une planète.