Very High Speed Integrated Circuit Hardware Description Language/Réalisation d'un coprocesseur CORDIC
Nous appellerons un coprocesseur dans la suite de ce cours tout périphérique suffisamment sophistiqué pour :
- faire des calculs arithmétiques au sens large
- nécessiter un processeur pour être testé
- éventuellement être capable d'exécuter un programme
Les GPU (des cartes graphiques) se rangent dans cette catégorie mais aussi les processeurs mathématiques (Unités de calcul en virgule flottante (ou FPU)) capables de calculer des fonctions simples ou compliquées comme les fonctions trigonométriques ou les fonctions hyperboliques.
Introduction à CORDIC
[modifier | modifier le wikicode]L'algorithme CORDIC est un algorithme itératif permettant de faire des calculs de fonctions trigonométriques, de fonctions hyperboliques ou de fonctions linéaires. Cet algorithme est difficile à appréhender lors d'une première approche. Heureusement, utiliser un algorithme ne nécessite pas de comprendre comment il fonctionne dans les détails. Mais sa modification ou son adaptation par contre le nécessite.
L'algorithme CORDIC est un algorithme capable de calculer un sinus et un cosinus sans aucune multiplication ! C'est ce qui lui donne toute son importance. Avant cet algorithme on ne connaissait que les développements limités qui eux nécessitent des multiplications et des divisions.
Il faudra cependant sauvegarder quelques valeurs en mémoire pour réaliser cet algorithme.
Domaines d'utilisation de l'algorithme CORDIC
[modifier | modifier le wikicode]L'algorithme CORDIC peut naturellement être simplement utilisé pour des calculs. Pourtant, dans un livre sur les processeurs enfouis, nous ne resterons pas dans le domaine de l'abstraction. Nous allons donc lui consacrer au moins deux domaines d’applications :
- robotique mobile : calcul des coordonnées x et y d'un robot se déplaçant à l'aide de deux moteurs à courant continu. Lisez AVR et robotique : ASURO dans un autre projet et particulièrement la section "Marier l'électronique et la cinématique" vous y trouverez des formules faisant intervenir des sinus et cosinus.
- commande de moteur synchrone
Propriétés des fonctions trigonométriques
[modifier | modifier le wikicode]Les calculs se font avec des nombres. Puisqu'ici nous désirons étudier des "sinus" et "cosinus" et que ces nombres sont entre 0 et 1 il nous faudra réfléchir sur la façon de représenter ces nombres. C'est l’objet de la prochaine section.
Représentation des nombres à virgule
[modifier | modifier le wikicode]Il existe au moins deux méthodes pour faire cela :
- la représentation virgule flottante
- la représentation virgule fixe
Nous allons présenter les deux méthodes même si nous avons l'intention de nous attarder beaucoup plus sur la virgule fixe.
La représentation virgule flottante
[modifier | modifier le wikicode]L'article Virgule_flottante de wikipédia est suffisamment complet pour ne pas être repris ici. Il peut d'ailleurs être complété par la lecture de l’article détaillé sur la norme IEEE 754 correspondante.
Voici en figure récapitulative le codage des nombres flottants.

Il existe essentiellement deux formats :
| Encodage | Signe | Exposant | Mantisse | Valeur d'un nombre | Précision | Chiffres significatifs | |
| Simple précision | 32 bits | 1 bit | 8 bits | 23 bits | 24 bits | environ 7 | |
| Double précision | 64 bits | 1 bit | 11 bits | 52 bits | 53 bits | environ 16 |
Sur ces deux formats, seul le format simple précision sur 32 bits nous intéresse. Il peut se résumer avec la figure :

Pour un nombre normalisé, le bit de poids fort de la mantisse est toujours à 1 et il n'est alors pas représenté. Il est alors qualifié de bit implicite. La conséquence est que l'expression du tableau pour la représentation 32 bits doit être comprise comme :
- une différence entre le M de la formule et la Mantisse : M = 1,Mantisse
- la valeur du nombre est donnée par
Si le bit de poids fort de la mantisse (ici bit 23 implicite) est nul (en général pour un exposant décalé nul) alors le nombre est dit dénormalisé.
La représentation virgule fixe
[modifier | modifier le wikicode]Le format Virgule fixe n’est pas normalisé contrairement au format virgule flottante. Le seul point commun que l’on retrouve dans tous les formats virgule fixe est qu’il est signé. Il peut donc représenter des nombres positifs ou négatifs en complément à 2. La virgule étant placée par défaut à un endroit fixe on utilise en général une notation du genre Qm.n pour le désigner où m représente le nombre de bits avant la virgule et n le nombre de bit après la virgule et donc m+n est la taille de la représentation.
Par exemple nous allons utiliser un format Q3.13 dans la suite de ce chapitre.
| S |
Il s'agit d'un format 16 bits (3+13) et adapté à la trigonométrie en radian.
La notation Q3.13 utilisée ici n’est pas universelle. Elle utilise donc le nombre de bits avant et après la virgule. On peut trouver dans la littérature spécialisée une notation qui utilise le nombre de bits total et le nombre de bits après la virgule. Ainsi notre notation Q3.13 devrait être remplacé par Q16.13 (nous avons trouvé aussi <16,13> dans Patrick R. Schaumont "A Practical Introduction to Hardware Software Codesign" Springer (2010)). Nous utiliserons systématiquement la première notation dans ce chapitre.
Pour manipuler ce format nous proposons quelques utilitaires en C. Ils sont basés sur le fait que la librairie standard du compilateur C sait manipuler les nombres à virgule à partir du moment où ils sont en virgule flottante. La lecture à partir du clavier ainsi que l’affichage sur un écran de ces nombres est aussi dans la librairie standard.
Une fois le format virgule fixe choisi, il vous faut commencer par mettre au point des routines de conversions. Il vous faudra en effet tester votre travail et elle pourront servir. Le format virgule fixe n'étant pas standard dans le c, nous vous proposons des routines de conversions vers les nombres flottant que le C sait afficher. Si vous changez de format virgule fixe il vous faut commencer par modifier ces routines.
Nous proposons donc deux routines permettant les transformations de notre format virgule fixe Q3.13 vers le format flottant.
Format Q3.13 vers flottant
[modifier | modifier le wikicode]Nous vous proposons deux sous-programmes destinés à une conversion du format Q3.13 vers le format float du C. Nous avons écrit ces sous-programme avec l'intention un jour de les implanter en matériel. C'est pour cela qu'ils peuvent vous paraître obscurs. En effet une simple division flottante peut naturellement faire l'affaire.
Sans entrer dans les détails, nous vous proposons des sous-programmes réservés aux architectures de type PC :
// Serge MOUTOU Avril 2013
// destiné à une architecture 32 bits et non aux AVRs ciblés
// Sur un PC cela fonctionne normalement
float HexQ3_13ToFloat(int val){ //conversion Q3.13 vers float
float temp;
int i_temp;
char i;
if (val < 0) i_temp = -val; else i_temp = val;
temp = ((i_temp & 0x6000)>>13);
for (i=0;i<13;i++)
if (i_temp & (1<<i)) temp += pow(2,(i-13));
if (val < 0) return -temp; else return temp;
}
//******* version sans pow
/**************************************************
/* Ne peut pas fonctionner avec AVR car
/* int et float n'ont pas la même taille !!!!
/**************************************************/
float HexQ3_13ToFloat2(int val){
union {
float temp;
int f_temp;
} u;
int i_temp;
unsigned char exposant=129;//,*p;
signed char i;
if (val < 0) i_temp = -val; else i_temp = val;
for (i=15;i>=0;i--) {
if (i_temp & (1<<i)) {
// on efface le '1' trouvé :
i_temp= i_temp & ~(1<<i);
break;// on sort de la boucle
}
exposant--;
}
u.f_temp = exposant;
u.f_temp <<=23;
u.f_temp = u.f_temp|(i_temp << (23-i));
if (val < 0) return -(u.temp); else return u.temp;
}
//******* version sans pow
/**************************************************
/* Version pour AVR : Arduino OK et SOC OK
/* Serge MOUTOU Fevrier 2019
/**************************************************/
float HexQ3_13ToFloat_AVR(int16_t val){
union {
float f_temp;
int32_t li_temp;
} u;
uint32_t i_temp;
unsigned char exposant=129;//,*p;
signed char i;
u.li_temp = 0;
if (val < 0) i_temp = -val; else i_temp = val;
for (i=15;i>=0;i--) {
if (i_temp & (1<<i)) {
// on efface le '1' trouvé :
i_temp= i_temp & ~(1<<i);
break;// on sort de la boucle
}
exposant--;
}
u.li_temp = exposant;
u.li_temp <<=23;
u.li_temp = u.li_temp|(i_temp << (23-i));
if (val < 0) return -(u.f_temp); else return u.f_temp;
}
- Le type "int" du c n’est pas défini de manière standard. Il peut être sur 16, 32 ou 64 bits. Il est de 16 bits sur AVR et de 32 bits sur un PC.
- Une simple division suffit à faire cette conversion : il suffit de diviser par 1 (soit 0x2000 en Q3.13). Nous avons choisi ces méthodes un peu complexe avec l'idée derrière la tête, de les matérialiser un jour
La deuxième routine n'utilisant pas "pow" n'a pas beaucoup d'intérêt pour un PC. Mais elle a été développée en vue d'un portage sur AVR, ce qui a été fait quelques années après (2019).
Comme nous l'avons énoncé au tout début de cette section, une simple routine universelle pourrait donc être réalisée par :
// Serge MOUTOU Juin 2018
// destiné à une architecture quelconque
float HexQ3_13ToFloat3(int val){ //conversion Q3.13 vers float
return (val * 1.0 / (0x2000)); // 0x2000 = 1 en Q3.13
}
Attachons-nous maintenant à la transformation inverse.
Format flottant vers Q3.13
[modifier | modifier le wikicode]La transformation du format flottant vers le Q3.13 se fait par :
// Serge MOUTOU Avril 2013
// destiné à une architecture 32 bits et non aux AVRs ciblés
// Sur un PC cela fonctionne normalement
int float2HexQ3_13(float val){ //conversion float vers Q3.13
int temp;
char i;
float f_temp;
if (val < 0) f_temp = -val; else f_temp = val;
temp = ((int) floor(f_temp)<<13);
f_temp = f_temp - floor(f_temp);
for (i=0;i<13;i++) {
temp|=((int)floor(2*f_temp)<<(12-i));
f_temp = 2*f_temp - floor(2*f_temp);
}
if (val < 0) return -temp; else return temp;
}
//************************************************************************
// function float2HexQ3_13_2()
// purpose: transformation of a 32-bit float number into 16-bit Q3.13 number
// arguments:
// corresponding float number
// return: 16-bit int
// note: This function works on Linux but not with AVR
//************************************************************************
typedef union {
float f_temp; //taille : {{unité|4|octets}}
int li_temp; //taille : {{unité|4|octets}}
} t_u;
// version sans calcul float
int float2HexQ3_13_2(float val){ //conversion float vers Q3.13
t_u u,v;
unsigned char exposant;
int mantisse;
int result=0;
u.f_temp = val;
if (val < 0) u.f_temp = - u.f_temp;
v = u;
// recupération de l'exposant
v.li_temp >>= 23;
exposant = v.li_temp;
// recuperation mantisse
if (exposant < 129) {
mantisse = (u.li_temp & 0X007FFFFF);
// mise à 1 du bit manquant
result |= (1 << (exposant-114)); // (15-129+exposant)); semble OK
mantisse >>= (137-exposant); //(22-(14-129+exposant));
result |= mantisse;
if (val < 0) return -result;
else return result;
} else {printf("Erreur conversion : nombre trop grand\n");
return 0x7FFF; // le plus qu'on puisse faire pour 16 bits
}
}
//************************************************************************
// function float2HexQ3_13_AVR()
// purpose: transformation of a 32-bit float number into Q3.13 for AVR
// arguments:
// corresponding float number
// return: integer in Q3.13 format
// note: idem to float2HexQ3_13 but without float library
// Juin 2018
//************************************************************************
int float2HexQ3_13_AVR(float val){ //conversion float vers Q3.13
union {
float f_temp; //taille : 4 octets
long int li_temp; //taille : 4 octets
} u,v;
unsigned char exposant;
long int mantisse;
int result=0;
u.f_temp = val;
if (val < 0) u.f_temp = - u.f_temp;
v = u;
// recupération de l'exposant
v.li_temp >>= 23;
exposant = v.li_temp;
// recuperation mantisse
if (exposant < 129) {
mantisse = (u.li_temp & 0X007FFFFF);
// mise à 1 du bit manquant
result |= (1 << (exposant-114)); // (15-129+exposant)); semble OK
mantisse >>= (137-exposant); //(22-(14-129+exposant));
result |= mantisse;
if (val < 0) return -result;
else return result;
} else {
//**** "Erreur conversion"*****
return 0;
}
}
Cette première routine ne contient pas de vérification d'erreur tandis que la deuxième affiche une erreur mais retourne quand même un nombre. Le format "float" du c étant plus précis que notre format Q3.13, cette routine peut échouer. Elle reste cependant utile dans le cadre de CORDIC.
Tests des deux routines précédentes avec un Arduino
[modifier | modifier le wikicode]Pour tester le bon fonctionnement des transformations de formats, rien de tel qu'un programme qui transforme dans les deux sens pour constater si oui ou non on retrouve le même résultat. Voici donc un exemple sous Arduino.
void setup() {
Serial.begin(9600);
}
int nb=0x1000; //0.5 en Q3.13
float fnb;
void loop() {
// put your main code here, to run repeatedly:
nb++;
fnb = HexQ3_13ToFloat_AVR(nb);
nb = float2HexQ3_13_AVR(fnb);
Serial.println(fnb,4);
delay(500);
}
//************************************************************************
// function float2HexQ3_13_AVR()
// purpose: transformation of a 32-bit float number into Q3.13
// arguments:
// corresponding float number
// return: integer in Q3.13 format
// note: idem to float2HexQ3_13 but without float library
// utilise 500 octets de moins que la précédente
//************************************************************************
int float2HexQ3_13_AVR(float val){ //conversion float vers Q3.13
union {
float f_temp; //taille : 4 octets
long int li_temp; //taille : 4 octets
} u,v;
unsigned char exposant;
long int mantisse;
int result=0;
u.f_temp = val;
if (val < 0) u.f_temp = - u.f_temp;
v = u;
// recupération de l'exposant
v.li_temp >>= 23;
exposant = v.li_temp;
// recuperation mantisse
if (exposant < 129) {
mantisse = (u.li_temp & 0X007FFFFF);
// mise à 1 du bit manquant
result |= (1 << (exposant-114)); // (15-129+exposant)); semble OK
mantisse >>= (137-exposant); //(22-(14-129+exposant));
result |= mantisse;
if (val < 0) return -result;
else return result;
} else {
//**** "Erreur conversion"*****
return 0;
}
}
float HexQ3_13ToFloat_AVR(int16_t val){
union {
float f_temp;
int32_t li_temp;
} u;
uint32_t i_temp;
unsigned char exposant=129;//,*p;
signed char i;
u.li_temp = 0;
if (val < 0) i_temp = -val; else i_temp = val;
for (i=15;i>=0;i--) {
if (i_temp & (1<<i)) {
// on efface le '1' trouvé :
i_temp= i_temp & ~(1<<i);
break;// on sort de la boucle
}
exposant--;
}
u.li_temp = exposant;
u.li_temp <<=23;
u.li_temp = u.li_temp|(i_temp << (23-i));
if (val < 0) return -(u.f_temp); else return u.f_temp;
}
Un peu de théorie sur CORDIC
[modifier | modifier le wikicode]
Dans cette section, nous allons détailler l'algorithme CORDIC. Nous présentons un schéma simplifié de principe de calcul où vous voyez apparaître trois entrées et trois sorties . Ce schéma est simplifié dans le sens où l’on a omis l'horloge en entrée (il faut bien une horloge pour faire avancer un calcul).
Les données à gauche représentent l'initialisation de l'algorithme. La donnée essentielle est qui représente un angle qui pour nous sera exprimé en radians. Les autres données seront prises comme et dans un premier temps pour expliquer l'algorithme.
Les sorties à droites représenteront le sinus et le cosinus ainsi que l'erreur réalisée sur l'angle.
Qu'y a-t-il dans le bloc ? Un ensemble de trois équations de récurrences que nous allons examiner maintenant.
Des équations de récurrences simples
[modifier | modifier le wikicode]
Nous avons au départ trois équations de récurrences simples :
avec .
On expliquera plus tard les relations
et (constantes prédéfinies).
Ce que font ces trois équations est représenté sur la figure ci-contre où les variables ont été remplacées par une notation plus conventionnelle pour des angles. Nous allons expliciter cette figure maintenant.
Dans cette figure vous voyez apparaître un ensemble de rotations qui aboutissent à l'angle dont on cherche le sinus et le cosinus (vecteur rouge de la figure). Vous avez certainement remarqué que les rotations ne sont pas des vraies rotations (qui conservent les longueur) puisqu'elles sont systématiquement associées à une dilatation. La dilatation dépend de l'angle mais :
- Pour trouver la longueur de dilatation par un certain angle il suffit de remarquer les angles droits de la figure.
- Si l’on appelle R, K et H (pour hypoténuse) les côtés du triangle, on a les relations :
- donc et ainsi
- (relation importante qui sera retrouvée autrement plus tard).
Ce qui n’apparaît pas sur la figure est que les angles sont déterminés à l'avance (on reviendra sur cette propriété plus tard).
- Quelle que soit la position du vecteur rouge (notre objectif), on peut trouver une séquence de rotations (positives et négatives) pour y parvenir.
- Quelle que soit la séquence de rotations exécutées, si elles sont assez nombreuses la dilatation finale sera toujours la même.
Ces trois propriétés justifient la méthode CORDIC. Mais regardons d'un peu de plus près les équations de récurrence et donnons-en quelques caractéristiques à travers des remarques.
Nous avons commencé ce chapitre en promettant aucune multiplication. Or les équations de récurrences font apparaître les termes . Nous espérons que le lecteur ayant suivi jusqu'à ce point se demande s'il a été dupé ? Examinons cela en détail.
La multiplication par n’est pas une multiplication car cette valeur est soit +1 (rien à faire) soit -1 (un complément à deux à réaliser). Or le complément à deux se réalise avec des inverseurs et une addition de 1 ! donc pas de multiplication.
Il nous reste donc les multiplications par à faire disparaître...
Maintenant que tous les lecteurs ont entraperçu une relation entre CORDIC et les rotations, nous allons examiner cela de manière un peu plus formelle.
Relation avec les rotations
[modifier | modifier le wikicode]Cette partie s'inspire un peu d'un sugjet d'agrégation Génie électrique (2006) : sujets agrégation. Les sujets d'agrégation ne sont pas soumis au copyright. De toute façon ce sujet d'agrégation a été fortement remanié pour le rendre plus accessible. Il en résulte un ensemble de questions avec ses solutions.
Écriture matricielle de CORDIC
[modifier | modifier le wikicode]Écrire les deux premières équations sous la forme matricielle en calculant la matrice Ci :
avec et . (On note donc tout simplement l'entrée et la sortie sous forme de deux composantes vectorielles pour pouvoir introduire cette matrice).
Comment introduire les matrices de rotation
[modifier | modifier le wikicode]La figure montre clairement un ensemble de rotations. Rappelons que les rotations dans un plan sont décrites par des matrices de rotation rappelées ci-après : (rotation d'angle α)
Cette matrice fait tourner le plan d'un angle α.
Elle peut être généralisée sous la forme indicée :
où le paramètre pour décrire le sens de rotation ( rotation dans le sens trigonométrique).
L'idée qui vient à l'esprit est donc de tenter d'écrire la matrice de la section précédente à l'aide d'une matrice de rotation
Écrire la matrice sous la forme en prenant soin d'expliciter et finalement .
qui donne immédiatement et devient :
Prenons du recul par rapport aux équations : en clair les relations de récurrences CORDIC réalisées par la matrice sont équivalentes à une rotation multipliée par qui est plus grand que 1. C'est donc équivalent à une rotation et une dilatation.
Tiens tiens, n'a-t-on pas déjà évoqué cette propriété dans ce chapitre d'une dilatation par ?
Arrivé à ce point, nous espérons que le lecteur a compris (ou au moins entrevu) la relation entre les équations de récurrences CORDIC et les rotations. Rappelons que l’on cherche à calculer un cosinus et un sinus. Il reste cependant des détails à régler pour faire fonctionner CORDIC.
Calculer les équations de récurrences
[modifier | modifier le wikicode]Soit la valeur initiale de , exprimer en fonction de , , , ... puis en fonction de , , , , ...
Il est temps de travailler sur la troisième équation de récurrence que nous avons laissé tombé jusqu'à présent.
Travail sur les angles
[modifier | modifier le wikicode]Premier détail : nous allons prendre à partir de maintenant . C'est cette subtilité qui fait toute la valeur de l'algorithme CORDIC. Pourquoi ? Parce que ce terme apparaît toujours comme terme multiplicatif dans les équations de récurrences :
et qu'une propriété intéressante d'une multiplication par une puissance de 2 est qu'elle peut être remplacée par un simple décalage. Autrement dit choisir va permettre d'économiser des multiplications (qui est un opérateur arithmétique considéré comme complexe, lent et cher).
La relation entre une multiplication par une puissance de deux et un décalage n’est pas universelle. Elle dépend de la représentation du nombre. Par exemple elle n’est pas vraie pour un nombre en virgule flottante... où cette opération doit être remplacée par une addition sur l'exposant.
Ceux qui ont suivi nous rétorquerons que les multiplications ont été remplacées par dans la troisième équation de récurrence. Remplacer des multiplications par des calculs de tangente inverse est-ce un progrès ? Certes non, mais ces valeurs peuvent être pré-calculées et sauvées dans une mémoire.
Calculer pour i=0, 1, 2, ..., 13 si, comme on le rappelle, (question précédente).
Réponse : On donne les valeurs précalculées :
| i | αi = tan−1 (2−i) | |
|---|---|---|
| Degrees | Radians | |
| 0 | 45.00 | 0.7854 |
| 1 | 26.57 | 0.4636 |
| 2 | 14.04 | 0.2450 |
| 3 | 7.13 | 0.1244 |
| 4 | 3.58 | 0.0624 |
| 5 | 1.79 | 0.0312 |
| 6 | 0.90 | 0.0160 |
| 7 | 0.45 | 0.0080 |
| 8 | 0.2238 | 0.0039 |
| 9 | 0.1119 | 0.0019 |
| 10 | 0.05595 | 0.00098 |
| 11 | 0.02798 | 0.00049 |
| 12 | 0.01399 | 0.00024 |
| 13 | 0.00699 | 0.00012 |
Deuxième détail : nous avons laissé de côté qui est un signe + ou -. Il est grand temps de voir comment il est calculé. C'est tout simplement le signe de l'angle calculé : . Ce signe est connu (puisque l'est) lors du calcul. Le calcul précédent peut être réalisé tel quel dans du matériel (qui peut calculer en parallèle).
Les deux premières équations de récurrences dépendent de la troisième qui gère l'angle par le signe. Cependant, la troisième équation de récurrence est complètement indépendante des deux autres. Une des conséquences est que vous n'êtes pas obligé d’utiliser la même représentation virgule fixe (ou autre) pour cette troisième équation. Vous pouvez par exemple la faire fonctionner en degré (avec un format Q10.6 par exemple) alors que vos sinus et cosinus continueront d’être en Q3.13
Le problème du gain
[modifier | modifier le wikicode]Depuis le début de ce chapitre nous savons qu'un problème de gain était à prendre en compte. En effet, nous avons montré très tôt que l'algorithme réalisait en fait une rotation mais multiplié par . Pour avoir un cosinus et un sinus il nous faudra donc calculer et multiplier le résultat final par cette valeur.
On peut éviter cependant cette multiplication si au lieu d'initialiser à 1, on réalise : .
Les valeurs numériques correspondantes sont facilement évaluées avec un tableur ( d'inverse 0,60725).
Voila. Maintenant tous les détails de calculs sont en place. Pour mettre cela en œuvre dans un premier temps, nous allons utiliser un tableur et regarder CORDIC fonctionner puis nous ferons la même chose en langage C pur.
Utiliser un tableur pour faire fonctionner CORDIC
[modifier | modifier le wikicode]Nous nous proposons dans cette section d’utiliser le tableur LibreOffice pour examiner comment fonctionne CORDIC. Nous pensons, même si nous n'avons pas essayé, que EXEL utiliserait les mêmes primitives.
Nous allons décomposer le travail en deux parties.
Faire fonctionner la troisième équation de récurrence
[modifier | modifier le wikicode]La troisième équation de récurrence est un calcul d'angle en fonction de . Comme nous l'avons déjà affirmé, cette équation peut fonctionner seule. Voici comment on peut procéder avec un tableur (pour lequel les colonnes sont des lettres et les lignes des chiffres, format par défaut de LibreOffice):
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| 1 | i | delta_i | alpha_i | K_i | z_i | sigma_i |
| 2 | 0 | =PUISSANCE(2;-A2) | =ATAN(B2) | =1/COS(C2) | =PI()/3 | =SI(E2<0;-1;1) |
| 3 | 1 | =PUISSANCE(2;-A3) | =ATAN(B3) | =1/COS(C3) | =E2-C2*F2 | =SI(E3<0;-1;1) |
que l’on peut étendre vers le bas.
Le point essentiel du tableau est la case E2 (qui contient =PI()/3) qui est l'angle duquel on cherche le sinus et le cosinus. C'est la seule case à changer pour faire le calcul sur un autre angle.
L'intérêt d’utiliser un tableur est de voir comment varie cette variable z_i avec les itérations : elle converge toujours vers 0 !
Voici le résultat complet :
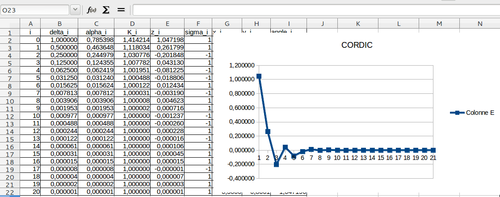
Ce graphe montre une convergence vers 0 qu’il n’est pas inutile de retenir pour comprendre les différentes utilisations de CORDIC évoquées plus loin.
Faire fonctionner l'ensemble
[modifier | modifier le wikicode]On complète le tableau par les deux colonnes représentant les deux équations manquantes (colonnes G et H) :
| A | B | C | D | E | F | G | H | I | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | i | delta_i | alpha_i | K_i | z_i | sigma_i | x_i | y_i | angle_i |
| 2 | 0 | =PUISSANCE(2;-A2) | =ATAN(B2) | =1/COS(C2) | =PI()/3 | =SI(E2<0;-1;1) | 0,6073 | 0 | 0 |
| 3 | 1 | =PUISSANCE(2;-A3) | =ATAN(B3) | =1/COS(C3) | =E2-C2*F2 | =SI(E3<0;-1;1) | =G2-F2*H2*B2 | = H2+G2*F2*B2 | =I2+F2*C2 |
On a ajouté pour information une colonne à droite qui calcule la somme des rotations pour montrer qu'elle converge bien vers l'angle souhaité.
Voici le résultat complet :

Encore une fois, seule la case E2 est à changer pour réaliser un autre calcul.
- Pour vos essais rappelez-vous que l'angle demandé en case E2 sur lequel vous calculez doit être en radian et entre et
- La troisième équation de récurrence peut être indistinctement celle sur ou celle sur . Mais alors le calcul du signe se fait différemment. Les dessins d'introduction montraient plutôt un angle qui convergeait vers l'angle final alors que notre premier algorithme CORDIC dans le tableur utilise .
Utiliser et adapter l'algorithme de Wikipédia
[modifier | modifier le wikicode]L'article CORDIC dans wikipédia propose un algorithme en C (enfin proposait : voir remarque ci-dessous). Prenez-le avec un copier coller et à l'aide d'un éditeur faites-en un fichier que l’on peut appeler "cordicWiki.c" par exemple. Sa compilation sous Linux ainsi que son exécution peut se faire par :
gcc -o cordic cordicWiki.c -lm ./cordic Veuillez entrer beta 0.785 Veuillez entrer le nombre d'iterations voulues 16 cos(beta) = 0.707431 , sin(beta) = 0.706892
Pour vos essais rappelez-vous que l'angle demandé sur lequel vous calculez doit être en radian et entre et . Nous savons très bien que nous nous répétons, mais c’est pour la bonne cause.
L'utilisation en cours de wikipédia nous amène à faire la remarque suivante :
Le programme en C qui était donné dans Wikipédia a disparu pour une raison qui nous échappe ! C'est dommage pour les enseignants qui l'utilisent dans leur cours !!! (Juin 2015)
Pour pallier à cet inconvénient, nous le remettons ici :
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
int main()
{
int nb_iter; // Nombre d'itérations
double K = 0.6073; // Valeur de K
double x = K, y = 0; // Valeur approchante de cos(beta) et sin(beta)
double x_Nouveau; // Variable temporaire
double z_i = 0; // Angle à chercher
double Pow2; // Valeur de la puissance de deux
printf("Calcul par la methode CORDIC de sinus : \n\n\n Veuillez entrer beta\n");
scanf("%lf",&z_i); // entrer la valeur de beta
printf("Veuillez entrer le nombre d'iterations voulues\n");
scanf("%d",&nb_iter); // Entrer le nombre d'itération
int i = 0; // declaration de l'indice d'iteration
for(i = 0; i < nb_iter; i++) {
Pow2 = pow(2,-i);
// Si beta<0 rotation dans le sens trigo
if(z_i < 0) {
x_Nouveau = x + y*Pow2;
y -= x*Pow2;
z_i += atan(Pow2);
}
// sinon dans l'autre sens
else {
x_Nouveau = x - y*Pow2;
y += x*Pow2;
z_i -= atan(Pow2);
}
x = x_Nouveau;
}
printf("cos(beta) = %lf , sin(beta) = %lf \n", x,y); // Affichage du résultat
return 0;
}
Le fonctionnement de cet algorithme semble parfait. Pourtant, nous allons essayer de l'améliorer pour un fonctionnement dans une architecture bien plus petite qu'un PC. En effet, compilé tel quel avec le compilateur avr-gcc, il faut plus de 8 ko de mémoire, ce qui n’est pas toujours possible pour certains processeurs (ATMega8 et ATTiny861) que nous utilisons dans ce cours.
Analyse des ressources calculs nécessaires
[modifier | modifier le wikicode]Une lecture de ce programme montre qu’il utilise le type "double" qui est le type flottant sur 64 bits. C'est un type peu adapté aux architectures 8 bits que nous désirons cibler.
Ce programme fonctionne avec les librairies de calcul en double (librairie mathématique qu'utilisent pow(2,-i) et atan(Pow2)) et nous désirons à tout prix l'éviter.
Simplifier le programme
[modifier | modifier le wikicode]La technique habituelle pour faire cette simplification est de choisir un format virgule fixe en lieu et place des variables de type "double". Nous allons utiliser le format Q3.13 qui veut dire que trois bits de poids forts sont la partie entière et les treize bits restants sont la partie fractionnaire.
D'autre part les multiplications par pow(2,-i) (soit avec des notations plus habituelles ) sont remplacées par de simples décalages comme cela a déjà été évoqué.
Enfin le calcul atan(Pow2) (soit avec des notations plus habituelles ) sera remplacé par un tableau de valeurs pré-calculées.
Ce travail a déjà été fait dans ICI (dans un autre livre) où vous avez un programme complet sans aucune multiplication.
Problème d'arrondi
[modifier | modifier le wikicode]Sans entrer dans les détails, notons que cet algorithme peut être amélioré. Toute représentation des nombres présente des imperfections. Ici, supposons que l’on ait 0xFFFF en format Q3.13. Un décalage vers la droite le transformerait en 0xFFFF alors qu’il faudrait le transformer en 0x0000 !
Voir aussi
[modifier | modifier le wikicode]
Après avoir examiné CORDIC d'une manière logicielle, nous allons nous intéresser maintenant à sa réalisation matérielle. Autre manière de dire les choses, le calcul devra donc être réalisé par une partie matérielle adaptée.
Implantation matérielle de l'algorithme CORDIC
[modifier | modifier le wikicode]Il y a typiquement deux façons de réaliser un coprocesseur CORDIC :
- utilisation d'un pipeline
- utilisation d'un séquenceur
En effet, un algorithme récursif représente une boucle et il y a deux moyens pour la réaliser : la séquencer (avec un compteur) comme on le ferait en programmation, ou la développer.
Nous allons présenter les deux façons maintenant.
Réalisation avec pipeline
[modifier | modifier le wikicode]La réalisation avec pipeline se fait de la manière suivante :

| Dans cette figure le signe se propage sur les trois additionneur soustracteur de l'étage ! |
Nous avons réalisé ce cœur sans utiliser les boucles du VHDL ce qui allonge un peu le code de ce coprocesseur CORDIC, c’est pourquoi nous le mettons dans une boite déroulante.
-- Serge Moutou avril 2013
-- CORDIC en format virgule fixe Q3.13 et 13 étages pipelinés
library ieee;
use ieee.std_logic_1164.all;
use ieee.std_logic_arith.all;
use IEEE.STD_LOGIC_UNSIGNED.ALL;
--USE ieee.numeric_std.all;
entity sc_corproc is
port(
clk : in std_logic;
ena : in std_logic;
Ain : in std_logic_vector(15 downto 0);
sin : out std_logic_vector(15 downto 0);
cos : out std_logic_vector(15 downto 0));
end entity sc_corproc;
--ARCHITECTURE rtl OF sc_corproc IS
--BEGIN
-- PROCESS(clk) BEGIN
-- IF rising_edge(clk) THEN
-- cos <= Ain;
-- sin <= Ain+1;
-- END IF;
-- END PROCESS;
--END rtl;
ARCHITECTURE rtl OF sc_corproc IS
-- TYPE signed_array IS signed(15 DOWNTO 0);
SIGNAL x_array : std_logic_vector(15 DOWNTO 0);--signed_array;-- := (OTHERS =>'0');
SIGNAL y_array : std_logic_vector(15 DOWNTO 0);--signed_array;-- := (OTHERS =>'0');
SIGNAL z_array : std_logic_vector(15 DOWNTO 0);--signed_array;-- := (OTHERS =>'0');
SIGNAL x_array_1 : std_logic_vector(15 DOWNTO 0);--signed_array;-- := (OTHERS =>'0');
SIGNAL y_array_1 : std_logic_vector(15 DOWNTO 0);--signed_array;-- := (OTHERS =>'0');
SIGNAL z_array_1 : std_logic_vector(15 DOWNTO 0);
SIGNAL x_array_2 : std_logic_vector(15 DOWNTO 0);--signed_array;-- := (OTHERS =>'0');
SIGNAL y_array_2 : std_logic_vector(15 DOWNTO 0);--signed_array;-- := (OTHERS =>'0');
SIGNAL z_array_2 : std_logic_vector(15 DOWNTO 0);
SIGNAL x_array_3 : std_logic_vector(15 DOWNTO 0);--signed_array;-- := (OTHERS =>'0');
SIGNAL y_array_3 : std_logic_vector(15 DOWNTO 0);--signed_array;-- := (OTHERS =>'0');
SIGNAL z_array_3 : std_logic_vector(15 DOWNTO 0);
SIGNAL x_array_4 : std_logic_vector(15 DOWNTO 0);--signed_array;-- := (OTHERS =>'0');
SIGNAL y_array_4 : std_logic_vector(15 DOWNTO 0);--signed_array;-- := (OTHERS =>'0');
SIGNAL z_array_4 : std_logic_vector(15 DOWNTO 0);
SIGNAL x_array_5 : std_logic_vector(15 DOWNTO 0);--signed_array;-- := (OTHERS =>'0');
SIGNAL y_array_5 : std_logic_vector(15 DOWNTO 0);--signed_array;-- := (OTHERS =>'0');
SIGNAL z_array_5 : std_logic_vector(15 DOWNTO 0);
SIGNAL x_array_6 : std_logic_vector(15 DOWNTO 0);--signed_array;-- := (OTHERS =>'0');
SIGNAL y_array_6 : std_logic_vector(15 DOWNTO 0);--signed_array;-- := (OTHERS =>'0');
SIGNAL z_array_6 : std_logic_vector(15 DOWNTO 0);
SIGNAL x_array_7 : std_logic_vector(15 DOWNTO 0);--signed_array;-- := (OTHERS =>'0');
SIGNAL y_array_7 : std_logic_vector(15 DOWNTO 0);--signed_array;-- := (OTHERS =>'0');
SIGNAL z_array_7 : std_logic_vector(15 DOWNTO 0);
SIGNAL x_array_8 : std_logic_vector(15 DOWNTO 0);--signed_array;-- := (OTHERS =>'0');
SIGNAL y_array_8 : std_logic_vector(15 DOWNTO 0);--signed_array;-- := (OTHERS =>'0');
SIGNAL z_array_8 : std_logic_vector(15 DOWNTO 0);
SIGNAL x_array_9 : std_logic_vector(15 DOWNTO 0);--signed_array;-- := (OTHERS =>'0');
SIGNAL y_array_9 : std_logic_vector(15 DOWNTO 0);--signed_array;-- := (OTHERS =>'0');
SIGNAL z_array_9 : std_logic_vector(15 DOWNTO 0);
SIGNAL x_array_10 : std_logic_vector(15 DOWNTO 0);--signed_array;-- := (OTHERS =>'0');
SIGNAL y_array_10 : std_logic_vector(15 DOWNTO 0);--signed_array;-- := (OTHERS =>'0');
SIGNAL z_array_10 : std_logic_vector(15 DOWNTO 0);
SIGNAL x_array_11 : std_logic_vector(15 DOWNTO 0);--signed_array;-- := (OTHERS =>'0');
SIGNAL y_array_11 : std_logic_vector(15 DOWNTO 0);--signed_array;-- := (OTHERS =>'0');
SIGNAL z_array_11 : std_logic_vector(15 DOWNTO 0);
SIGNAL x_array_12 : std_logic_vector(15 DOWNTO 0);--signed_array;-- := (OTHERS =>'0');
SIGNAL y_array_12 : std_logic_vector(15 DOWNTO 0);--signed_array;-- := (OTHERS =>'0');
SIGNAL z_array_12 : std_logic_vector(15 DOWNTO 0);
SIGNAL x_array_13 : std_logic_vector(15 DOWNTO 0);--signed_array;-- := (OTHERS =>'0');
SIGNAL y_array_13 : std_logic_vector(15 DOWNTO 0);--signed_array;-- := (OTHERS =>'0');
-- SIGNAL z_array_13 : std_logic_vector(15 DOWNTO 0);
-- SIGNAL x_ip : std_logic_vector(15 DOWNTO 0);
-- SIGNAL y_ip : std_logic_vector(15 DOWNTO 0);
BEGIN
--convert inputs into signed format
PROCESS(clk)
BEGIN
-- IF ena = '0' THEN
-- x_ip <= x"136F"; -- = 0.6073 en format Q3.13 ;
-- z_ip <= (OTHERS => '0');
-- y_ip <= (OTHERS => '0');
IF rising_edge(clk) THEN
IF Ain(15) = '1' THEN
-- x_array <= (x_ip) + (y_ip);
-- y_array <= (y_ip) - (x_ip);
x_array <= x"136F";
y_array <= 0 - x"136F";
z_array <= (Ain) + x"1921";--tan_array(0);
ELSE
x_array <= x"136F";
y_array <= x"136F";
z_array <= (Ain) - x"1921";--tan_array(0);
-- z_array <= x"2181"- x"1921";--tan_array(0);
END IF;
IF z_array(15) = '1' THEN
x_array_1 <= x_array + (y_array(15) & y_array(15 downto 1));
y_array_1 <= y_array - (x_array(15) & x_array(15 downto 1));
z_array_1 <= z_array + x"0ED6";
ELSE
x_array_1 <= x_array - (y_array(15) & y_array(15 downto 1));
y_array_1 <= y_array + (x_array(15) & x_array(15 downto 1));
z_array_1 <= z_array - x"0ED6";
END IF;
IF z_array_1(15) = '1' THEN
x_array_2 <= x_array_1 + (y_array_1(15) & y_array_1(15) & y_array_1(15 downto 2));
y_array_2 <= y_array_1 - (x_array_1(15) & x_array_1(15) & x_array_1(15 downto 2));
z_array_2 <= z_array_1 + x"07D6";
ELSE
x_array_2 <= x_array_1 - (y_array_1(15) & y_array_1(15) & y_array_1(15 downto 2));
y_array_2 <= y_array_1 + (x_array_1(15) & x_array_1(15) & x_array_1(15 downto 2));
z_array_2 <= z_array_1 - x"07D6";
END IF;
IF z_array_2(15) = '1' THEN
x_array_3 <= x_array_2 + (y_array_2(15) & y_array_2(15) & y_array_2(15) & y_array_2(15 downto 3));
y_array_3 <= y_array_2 - (x_array_2(15) & x_array_2(15) & x_array_2(15) & x_array_2(15 downto 3));
z_array_3 <= z_array_2 + x"03FA";
ELSE
x_array_3 <= x_array_2 - (y_array_2(15) & y_array_2(15) & y_array_2(15) & y_array_2(15 downto 3));
y_array_3 <= y_array_2 + (x_array_2(15) & x_array_2(15) & x_array_2(15) & x_array_2(15 downto 3));
z_array_3 <= z_array_2 - x"03FA";
END IF;
IF z_array_3(15) = '1' THEN
x_array_4 <= x_array_3 + (y_array_3(15) & y_array_3(15) & y_array_3(15) &
y_array_3(15) & y_array_3(15 downto 4));
y_array_4 <= y_array_3 - (x_array_3(15) & x_array_3(15) & x_array_3(15) &
x_array_3(15) & x_array_3(15 downto 4));
z_array_4 <= z_array_3 + x"01FF";
ELSE
x_array_4 <= x_array_3 - (y_array_3(15) & y_array_3(15) & y_array_3(15) &
y_array_3(15) & y_array_3(15 downto 4));
y_array_4 <= y_array_3 + (x_array_3(15) & x_array_3(15) & x_array_3(15) &
x_array_3(15) & x_array_3(15 downto 4));
z_array_4 <= z_array_3 - x"01FF";
END IF;
IF z_array_4(15) = '1' THEN
x_array_5 <= x_array_4 + (y_array_4(15) & y_array_4(15) & y_array_4(15) &
y_array_4(15) & y_array_4(15) & y_array_4(15 downto 5));
y_array_5 <= y_array_4 - (x_array_4(15) & x_array_4(15) & x_array_4(15) &
x_array_4(15) & x_array_4(15) & x_array_4(15 downto 5));
z_array_5 <= z_array_4 + x"00FF";
ELSE
x_array_5 <= x_array_4 - (y_array_4(15) & y_array_4(15) & y_array_4(15) &
y_array_4(15) & y_array_4(15) & y_array_4(15 downto 5));
y_array_5 <= y_array_4 + (x_array_4(15) & x_array_4(15) & x_array_4(15) &
x_array_4(15) & x_array_4(15) & x_array_4(15 downto 5));
z_array_5 <= z_array_4 - x"00FF";
END IF;
IF z_array_5(15) = '1' THEN
x_array_6 <= x_array_5 + (y_array_5(15) & y_array_5(15) & y_array_5(15) &
--y_array_5(15) & y_array_5(15) & y_array_5(15) & y_array_5(15) & y_array_5(15 downto 6));
y_array_5(15) & y_array_5(15) & y_array_5(15) & y_array_5(15 downto 6));
y_array_6 <= y_array_5 - (x_array_5(15) & x_array_5(15) & x_array_5(15) &
--x_array_5(15) & x_array_5(15) & x_array_5(15) & x_array_5(15) & x_array_5(15 downto 6));
x_array_5(15) & x_array_5(15) & x_array_5(15) & x_array_5(15 downto 6));
z_array_6 <= z_array_5 + x"007F";
ELSE
x_array_6 <= x_array_5 - (y_array_5(15) & y_array_5(15) & y_array_5(15) &
y_array_5(15) & y_array_5(15) & y_array_5(15) & y_array_5(15 downto 6));
y_array_6 <= y_array_5 + (x_array_5(15) & x_array_5(15) & x_array_5(15) &
x_array_5(15) & x_array_5(15) & x_array_5(15) & x_array_5(15 downto 6));
z_array_6 <= z_array_5 - x"007F";
END IF;
IF z_array_6(15) = '1' THEN
x_array_7 <= x_array_6 + (y_array_6(15) & y_array_6(15) & y_array_6(15) &
y_array_6(15) & y_array_6(15) & y_array_6(15) & y_array_6(15) &
y_array_6(15 downto 7));
y_array_7 <= y_array_6 - (x_array_6(15) & x_array_6(15) & x_array_6(15) &
x_array_6(15) & x_array_6(15) & x_array_6(15) & x_array_6(15) &
x_array_6(15 downto 7));
z_array_7 <= z_array_6 + x"003F";
ELSE
x_array_7 <= x_array_6 - (y_array_6(15) & y_array_6(15) & y_array_6(15) &
y_array_6(15) & y_array_6(15) & y_array_6(15) & y_array_6(15) &
y_array_6(15 downto 7));
y_array_7 <= y_array_6 + (x_array_6(15) & x_array_6(15) & x_array_6(15) &
x_array_6(15) & x_array_6(15) & x_array_6(15) & x_array_6(15) &
x_array_6(15 downto 7));
z_array_7 <= z_array_6 - x"003F";
END IF;
IF z_array_7(15) = '1' THEN
x_array_8 <= x_array_7 + (y_array_7(15) & y_array_7(15) & y_array_7(15) &
y_array_7(15) & y_array_7(15) & y_array_7(15) & y_array_7(15) & y_array_7(15) &
y_array_7(15 downto 8));
y_array_8 <= y_array_7 - (x_array_7(15) & x_array_7(15) & x_array_7(15) &
x_array_7(15) & x_array_7(15) & x_array_7(15) & x_array_7(15) & x_array_7(15) &
x_array_7(15 downto 8));
z_array_8 <= z_array_7 + x"001F";
ELSE
x_array_8 <= x_array_7 - (y_array_7(15) & y_array_7(15) & y_array_7(15) &
y_array_7(15) & y_array_7(15) & y_array_7(15) & y_array_7(15) & y_array_7(15) &
y_array_7(15 downto 8));
y_array_8 <= y_array_7 + (x_array_7(15) & x_array_7(15) & x_array_7(15) &
x_array_7(15) & x_array_7(15) & x_array_7(15) & x_array_7(15) & x_array_7(15) &
x_array_7(15 downto 8));
z_array_8 <= z_array_7 - x"001F";
END IF;
IF z_array_8(15) = '1' THEN
x_array_9 <= x_array_8 + (y_array_8(15) & y_array_8(15) & y_array_8(15) &
y_array_8(15) & y_array_8(15) & y_array_8(15) & y_array_8(15) & y_array_8(15) &
y_array_8(15) & y_array_8(15 downto 9));
y_array_9 <= y_array_8 - (x_array_8(15) & x_array_8(15) & x_array_8(15) &
x_array_8(15) & x_array_8(15) & x_array_8(15) & x_array_8(15) & x_array_8(15) &
x_array_8(15) & x_array_8(15 downto 9));
z_array_9 <= z_array_8 + x"000F";
ELSE
x_array_9 <= x_array_8 - (y_array_8(15) & y_array_8(15) & y_array_8(15) &
y_array_8(15) & y_array_8(15) & y_array_8(15) & y_array_8(15) & y_array_8(15) &
y_array_8(15) & y_array_8(15 downto 9));
y_array_9 <= y_array_8 + (x_array_8(15) & x_array_8(15) & x_array_8(15) &
x_array_8(15) & x_array_8(15) & x_array_8(15) & x_array_8(15) & x_array_8(15) &
x_array_8(15) & x_array_8(15 downto 9));
z_array_9 <= z_array_8 - x"000F";
END IF;
IF z_array_9(15) = '1' THEN
x_array_10 <= x_array_9 + (y_array_9(15) & y_array_9(15) & y_array_9(15) &
y_array_9(15) & y_array_9(15) & y_array_9(15) & y_array_9(15) & y_array_9(15) &
y_array_9(15) & y_array_9(15) & y_array_9(15 downto 10));
y_array_10 <= y_array_9 - (x_array_9(15) & x_array_9(15) & x_array_9(15) &
x_array_9(15) & x_array_9(15) & x_array_9(15) & x_array_9(15) & x_array_9(15) &
x_array_9(15) & x_array_9(15) & x_array_9(15 downto 10));
z_array_10 <= z_array_9 + x"0007";
ELSE
x_array_10 <= x_array_9 - (y_array_9(15) & y_array_9(15) & y_array_9(15) &
y_array_9(15) & y_array_9(15) & y_array_9(15) & y_array_9(15) & y_array_9(15) &
y_array_9(15) & y_array_9(15) & y_array_9(15 downto 10));
y_array_10 <= y_array_9 + (x_array_9(15) & x_array_9(15) & x_array_9(15) &
x_array_9(15) & x_array_9(15) & x_array_9(15) & x_array_9(15) & x_array_9(15) &
x_array_9(15) & x_array_9(15) & x_array_9(15 downto 10));
z_array_10 <= z_array_9 - x"0007";
END IF;
IF z_array_10(15) = '1' THEN
x_array_11 <= x_array_10 + (y_array_10(15) & y_array_10(15) & y_array_10(15) &
y_array_10(15) & y_array_10(15) & y_array_10(15) & y_array_10(15) & y_array_10(15) &
y_array_10(15) & y_array_10(15) & y_array_10(15) & y_array_10(15 downto 11));
y_array_11 <= y_array_10 - (x_array_10(15) & x_array_10(15) & x_array_10(15) &
x_array_10(15) & x_array_10(15) & x_array_10(15) & x_array_10(15) & x_array_10(15) &
x_array_10(15) & x_array_10(15) & x_array_10(15) & x_array_10(15 downto 11));
z_array_11 <= z_array_10 + x"0003";
ELSE
x_array_11 <= x_array_10 - (y_array_10(15) & y_array_10(15) & y_array_10(15) &
y_array_10(15) & y_array_10(15) & y_array_10(15) & y_array_10(15) & y_array_10(15) &
y_array_10(15) & y_array_10(15) & y_array_10(15) & y_array_10(15 downto 11));
y_array_11 <= y_array_10 + (x_array_10(15) & x_array_10(15) & x_array_10(15) &
x_array_10(15) & x_array_10(15) & x_array_10(15) & x_array_10(15) & x_array_10(15) &
x_array_10(15) & x_array_10(15) & x_array_10(15) & x_array_10(15 downto 11));
z_array_11 <= z_array_10 - x"0003";
END IF;
IF z_array_11(15) = '1' THEN
x_array_12 <= x_array_11 + (y_array_11(15) & y_array_11(15) & y_array_11(15) & y_array_11(15) &
y_array_11(15) & y_array_11(15) & y_array_11(15) & y_array_11(15) & y_array_11(15) & y_array_11(15) &
y_array_11(15) & y_array_11(15) & y_array_11(15 downto 12));
y_array_12 <= y_array_11 - (x_array_11(15) & x_array_11(15) & x_array_11(15) &
x_array_11(15) & x_array_11(15) & x_array_11(15) & x_array_11(15) & x_array_11(15) & x_array_11(15) &
x_array_11(15) & x_array_11(15) & x_array_11(15 downto 12));
z_array_12 <= z_array_11 + x"0002";
ELSE
x_array_12 <= x_array_11 - (y_array_11(15) & y_array_11(15) & y_array_11(15) & y_array_11(15) &
y_array_11(15) & y_array_11(15) & y_array_11(15) & y_array_11(15) & y_array_11(15) & y_array_11(15) &
y_array_11(15) & y_array_11(15) & y_array_11(15 downto 12));
y_array_12 <= y_array_11 + (x_array_11(15) & x_array_11(15) & x_array_11(15) & x_array_11(15) &
x_array_11(15) & x_array_11(15) & x_array_11(15) & x_array_11(15) & x_array_11(15) & x_array_11(15) &
x_array_11(15) & x_array_11(15) & x_array_11(15 downto 12));
z_array_12 <= z_array_11 - x"0002";
END IF;
IF z_array_12(15) = '1' THEN
x_array_13 <= x_array_12 + (y_array_12(15) & y_array_12(15) & y_array_12(15) & y_array_12(15) &
y_array_12(15) & y_array_12(15) & y_array_12(15) & y_array_12(15) & y_array_12(15) & y_array_12(15) &
y_array_12(15) & y_array_12(15) & y_array_12(15) & y_array_12(15 downto 13));
y_array_13 <= y_array_12 - (x_array_12(15) & x_array_12(15) & x_array_12(15) & x_array_12(15) &
x_array_12(15) & x_array_12(15) & x_array_12(15) & x_array_12(15) & x_array_12(15) &
x_array_12(15) & x_array_12(15) & x_array_12(15) & x_array_12(15) & x_array_12(15 downto 13));
-- z_array_13 <= z_array_12 + x"0001";
ELSE
x_array_13 <= x_array_12 - (y_array_12(15) & y_array_12(15) & y_array_12(15) & y_array_12(15) &
y_array_12(15) & y_array_12(15) & y_array_12(15) & y_array_12(15) & y_array_12(15) & y_array_12(15) &
y_array_12(15) & y_array_12(15) & y_array_12(15) & y_array_12(15 downto 13));
y_array_13 <= y_array_12 + (x_array_12(15) & x_array_12(15) & x_array_12(15) & x_array_12(15) &
x_array_12(15) & x_array_12(15) & x_array_12(15) & x_array_12(15) & x_array_12(15) & x_array_12(15) &
x_array_12(15) & x_array_12(15) & x_array_12(15) & x_array_12(15 downto 13));
-- z_array_13 <= z_array_12 - x"0001";
END IF;
END IF;
END PROCESS;
cos <= x_array_13;
sin <= y_array_13;
END rtl;
Ce code n'a pas été développé avec une boucle VHDL pour des raisons d'optimisation.
Passons maintenant à la version séquentielle de ce même coprocesseur.
Réalisation séquentielle
[modifier | modifier le wikicode]Gilles Millon, Maître de conférences à l’IUT de Troyes, a fait une modification du cœur précédent pour qu’il fasse le même calcul mais de manière séquentielle. Nous allons en présenter son schéma de principe (et non son code complet) car il est encore utilisé en enseignement. Son principe est décrit dans la figure ci-contre.

Augmenter l'intervalle de calcul des angles
[modifier | modifier le wikicode]Gilles Millon a profité du passage du mode pipeline au mode séquentiel pour réaliser un coprocesseur CORDIC capable de traiter des angles de à au lieu de à . Ceci peut être fait avec le code VHDL suivant :
-- pretraitement angle
process(angle) begin
if ( angle>=zero and angle< ppi_2) then -- 0<angle<pi/2
s_angle <= angle;
coeffx <= '1'; -- +1
coeffy <= '1'; -- +1
elsif ( angle>ppi_2 and angle<ppi) then -- pi/2<angle<pi
s_angle <= ppi - angle ;
coeffx <= '0'; -- -1
coeffy <= '1'; -- +1
elsif ( angle>=mpi_2 and angle<=x"FFFF") then -- -pi/2<angle<0
s_angle <= angle;
coeffx <= '1'; -- +1
coeffy <= '0'; -- -1
elsif ( angle>=mpi and angle<=mpi_2) then -- -pi<angle<-pi/2
s_angle <= ppi - ( not(angle) +1 ) ;
coeffx <= '0'; -- -1
coeffy <= '0'; -- -1
else
s_angle <= angle;
coeffx <= '1';
coeffy <= '1';
end if;
end process;
où vous voyez une mémorisation dans coeffx et coeffy du quadrant concerné.
Version presque complète du coprocesseur CORDIC séquentiel
[modifier | modifier le wikicode]
Nous présentons maintenant la version presque complète du processeur CORDIC séquentiel. Ce qui manque a été demandé plusieurs fois à des étudiants :
et sera certainement demandé encore (d'où sa suppression). Il s'agit du séquenceur de trois états que nous allons décrire maintenant et que vous pouvez trouver après les commentaire "--TODO" dans le code un peu plus loin.
Voici de manière schématique ci-contre,l'ensemble à réaliser. Portez votre attention surtout sur le séquenceur, c’est lui qu’il faudra ajouter au code VHDL.
Et voici le code correspondant sans le séquenceur :
library ieee;
use ieee.std_logic_1164.all;
use ieee.std_logic_arith.all;
use IEEE.STD_LOGIC_UNSIGNED.ALL;
use ieee.numeric_std.all;
entity cordic_fsm_style is
port(
clk : in std_logic;
cordicstart : in std_logic;
fsminit : in std_logic; -- initialisation de la fsm en cas de probleme
angle : in std_logic_vector(15 downto 0);
sin : out std_logic_vector(15 downto 0);
cos : out std_logic_vector(15 downto 0);
cordicdone : out std_logic);
end entity;
architecture behavior of cordic_fsm_style is
constant k : std_logic_vector(15 downto 0) := x"136e"; -- constante k
constant maxit : std_logic_vector(3 downto 0) := x"d"; -- nombre d'iterations
constant ppi : std_logic_vector(15 downto 0) := x"6488"; -- +pi
constant ppi_2 : std_logic_vector(15 downto 0) := x"3245"; -- +pi/2
constant mpi : std_logic_vector(15 downto 0) := x"9B79"; -- -pi
constant mpi_2 : std_logic_vector(15 downto 0) := x"CDBD"; -- -pi/2
constant zero : std_logic_vector(15 downto 0) := x"0000"; -- angle 0
signal xi,xi1: std_logic_vector(15 downto 0);
signal yi,yi1: std_logic_vector(15 downto 0);
signal mui,mui1 : std_logic;
signal alphai,alphai1 : std_logic_vector(15 downto 0);
signal zi,zi1 : std_logic_vector(15 downto 0);
signal s_angle : std_logic_vector(15 downto 0);
signal coeffx,coeffy : std_logic;
signal i :std_logic_vector(3 downto 0);
signal y_divided,x_divided:std_logic_vector(15 downto 0);
signal encordic,initcordic : std_logic;
type etat is (e0,e1,e2);
signal state : etat;
component div2_i is port (
i : in std_logic_vector(3 downto 0);
ni : in std_logic_vector(15 downto 0);
n_divided : out std_logic_vector(15 downto 0)
);
end component;
begin
-- pretraitement angle
process(angle) begin
if ( angle>=zero and angle< ppi_2) then -- 0<angle<pi/2
s_angle <= angle;
coeffx <= '1'; -- +1
coeffy <= '1'; -- +1
elsif ( angle>ppi_2 and angle<ppi) then -- pi/2<angle<pi
s_angle <= ppi - angle ;
coeffx <= '0'; -- -1
coeffy <= '1'; -- +1
elsif ( angle>=mpi_2 and angle<=x"FFFF") then -- -pi/2<angle<0
s_angle <= angle;
coeffx <= '1'; -- +1
coeffy <= '0'; -- -1
elsif ( angle>=mpi and angle<=mpi_2) then -- -pi<angle<-pi/2
s_angle <= ppi - ( not(angle) +1 ) ;
coeffx <= '0'; -- -1
coeffy <= '0'; -- -1
else
s_angle <= angle;
coeffx <= '1';
coeffy <= '1';
end if;
end process;
-- description memoire des atan sous forme combinatoire
with i select
alphai <= x"1921" when x"0",
x"0ed6" when x"1",
x"07d6" when x"2",
x"03fa" when x"3",
x"01ff" when x"4",
x"00ff" when x"5",
x"007f" when x"6",
x"003f" when x"7",
x"001f" when x"8",
x"000f" when x"9",
x"0007" when x"a",
x"0003" when x"b",
x"0002" when x"c",
x"0001" when x"d",
x"0000" when x"e",
x"0000" when others;
-- calcul de mui1
mui <=zi(15);
-- calcul de zi
zi1_process: process(zi,mui,alphai) begin
if mui='1' then
zi1 <= zi + alphai;
else
zi1 <= zi - alphai;
end if;
end process;
-- multiplication par 2 puissance -i : x
-- <=> division par 2 puissance i
div_x_2_i : div2_i port map (i=> i, ni=> xi, n_divided => x_divided);
-- multiplication par 2 puissance -i : y
-- <=> division par 2 puissance i
div_y_2_i : div2_i port map (i=> i, ni=> yi, n_divided => y_divided);
-- calcul de xi1
xi1_process : process(mui,y_divided,xi) begin
if mui='1' then
xi1 <= xi + y_divided;
else
xi1 <= xi - y_divided;
end if;
end process;
-- calcul de yi1
yi1_process : process(mui,yi,x_divided) begin
if mui='1' then
yi1 <= yi - x_divided;
else
yi1 <= yi + x_divided;
end if;
end process;
-- mise à jour
-- cas particulier d'initialisation de x=k et y=0
-- pour calcul de sinus et cosinus
-- 13 itérations
iteration:process(clk,initcordic) begin
if initcordic='1' then
xi <=k;
yi <= (others => '0');
i <= (others=> '0');
zi <= s_angle;
elsif rising_edge(clk) then
if encordic = '1' then
if i<maxit then
xi <= xi1;
yi <= yi1;
zi <= zi1;
i <= i + 1;
end if;
end if;
end if;
end process;
--TODO : sequenceur A COMPLETER
cordic_seq: process(clk,fsminit) begin
if fsminit='1' then
state <= e0;
elsif rising_edge(clk) then
case state is
when e0 => if cordicstart='1' then
state <= e1;
else
state <= e0;
end if;
when e1 =>
when e2 =>
when others => state <= e0;
end case;
end if;
end process;
--TODO : actions du sequenceur ( A COMPLETER )
initcordic <= '1' when state=e0 else '0';
-- memorisation des valeurs du sinus et du cosinus en registre
-- a la fin des calculs ( sinon on voit l'évolution en temps réel
-- du calcul pendant les 13 itérations )
-- et ajustement du cos et du sin dans le cadre du traitement d'angle -pi à +pi
process(clk) begin
if rising_edge(clk) then
if state=e2 then
if coeffx='0' then
cos <= not (xi) +1;
else
cos <= xi;
end if;
if coeffy='0' then
sin <= not(yi) +1;
else
sin<=yi;
end if;
end if;
end if;
end process;
end behavior;
--------------------------------------------------------------------------
-- division par 2 puissance i
library ieee;
use ieee.std_logic_1164.all;
use ieee.std_logic_arith.all;
use IEEE.STD_LOGIC_UNSIGNED.ALL;
entity div2_i is port (
i : in std_logic_vector(3 downto 0);
ni : in std_logic_vector(15 downto 0);
n_divided : out std_logic_vector(15 downto 0)
);
end entity;
architecture behavior of div2_i is
signal oth0,oth1 : std_logic_vector(15 downto 0);
begin
oth0<=x"0000";
oth1<=x"ffff";
process(i,ni(15))begin
case i is
when x"0" => n_divided <= ni;
when x"1" => if ni(15) ='1' then
n_divided <= oth1(0) & ni(15 downto 1);
else
n_divided <= oth0(0) & ni(15 downto 1);
end if;
when x"2" => if ni(15) ='1' then
n_divided <= oth1(1 downto 0) & ni(15 downto 2);
else
n_divided <= oth0(1 downto 0) & ni(15 downto 2);
end if;
when x"3" => if ni(15) ='1' then
n_divided <= oth1(2 downto 0) & ni(15 downto 3);
else
n_divided <= oth0(2 downto 0) & ni(15 downto 3);
end if;
when x"4" => if ni(15) ='1' then
n_divided <= oth1(3 downto 0) & ni(15 downto 4);
else
n_divided <= oth0(3 downto 0) & ni(15 downto 4);
end if;
when x"5" => if ni(15) ='1' then
n_divided <= oth1(4 downto 0) & ni(15 downto 5);
else
n_divided <= oth0(4 downto 0) & ni(15 downto 5);
end if;
when x"6" => if ni(15) ='1' then
n_divided <= oth1(5 downto 0) & ni(15 downto 6);
else
n_divided <= oth0(5 downto 0) & ni(15 downto 6);
end if;
when x"7" => if ni(15) ='1' then
n_divided <= oth1(6 downto 0) & ni(15 downto 7);
else
n_divided <= oth0(6 downto 0) & ni(15 downto 7);
end if;
when x"8" => if ni(15) ='1' then
n_divided <= oth1(7 downto 0) & ni(15 downto 8);
else
n_divided <= oth0(7 downto 0) & ni(15 downto 8);
end if;
when x"9" => if ni(15) ='1' then
n_divided <= oth1(8 downto 0) & ni(15 downto 9);
else
n_divided <= oth0(8 downto 0) & ni(15 downto 9);
end if;
when x"a" => if ni(15) ='1' then
n_divided <= oth1(9 downto 0) & ni(15 downto 10);
else
n_divided <= oth0(9 downto 0) & ni(15 downto 10);
end if;
when x"b" => if ni(15) ='1' then
n_divided <= oth1(10 downto 0) & ni(15 downto 11);
else
n_divided <= oth0(10 downto 0) & ni(15 downto 11);
end if;
when x"c" => if ni(15) ='1' then
n_divided <= oth1(11 downto 0) & ni(15 downto 12);
else
n_divided <= oth0(11 downto 0) & ni(15 downto 12);
end if;
when x"d" => if ni(15) ='1' then
n_divided <= oth1(12 downto 0) & ni(15 downto 13);
else
n_divided <= oth0(12 downto 0) & ni(15 downto 13);
end if;
when x"e" => if ni(15) ='1' then
n_divided <= oth1(13 downto 0) & ni(15 downto 14);
else
n_divided <= oth0(13 downto 0) & ni(15 downto 14);
end if;
when x"f" => if ni(15) ='1' then
n_divided <= oth1(14 downto 0) & ni(15 downto 15);
else
n_divided <= oth0(14 downto 0) & ni(15 downto 15);
end if;
when others => n_divided <= ni;
end case;
end process;
end behavior;
Toutes les précédentes présentations de CORDIC ne sont pas faciles à tester sans processeur. Nous allons nous intéresser maintenant à la réalisation d'une interface avec un processeur. Bien sûr les processeurs déjà utilisés dans ce cours auront notre préférence.
Transformer notre coprocesseur CORDIC en périphérique
[modifier | modifier le wikicode]Nous allons nous intéresser maintenant à l’utilisation du coprocesseur CORDIC par un processeur. Cela consiste donc à le transformer en périphérique.
Un périphérique pour l'ATMega
[modifier | modifier le wikicode]
Le processeur que nous avons utilisé le plus dans ce livre étant l'ATMega, nous allons nous intéresser à réaliser ce périphérique pour ce processeur. Comme nous l'avons déjà présenté dans Embarquer un Atmel ATMega8 et plus en détail dans Améliorer l'ATMega8 avec l'ATMega16 et l'ATMega32 nous allons reprendre la terminologie graphique correspondante. Rappelons donc que tout se passe dans un fichier appelé "io.vhd" dans lequel deux process sont présents :
- un pour l'écriture dans les PORTs/Registres : IOwr
- un pour la lecture des PORTs/registres : Iord
Si vous partez du coprocesseur CORDIC, vous voyez que son entrée "Ain(15:0)" est réalisée à l'aide de deux PORTs (PORTB et PORTA), que son entrée "Ena" est réalisée à l'aide d'un bit du PORTD.
Les sorties de ce coprocesseur deviennent PINA et PINB pour le sinus et PINC et PIND pour le cosinus.
Voici comment tout ceci est réalisé :
library IEEE;
use IEEE.STD_LOGIC_1164.ALL;
use IEEE.STD_LOGIC_ARITH.ALL;
use IEEE.STD_LOGIC_UNSIGNED.ALL;
--USE ieee.numeric_std.all;
entity io is
port ( I_CLK : in std_logic; --25MHz
I_CLR : in std_logic;
I_ADR_IO : in std_logic_vector( 7 downto 0);
I_DIN : in std_logic_vector( 7 downto 0);
I_RD_IO : in std_logic;
I_RX : in std_logic;
I_WE_IO : in std_logic;
Q_DOUT : out std_logic_vector( 7 downto 0);
Q_INTVEC : out std_logic_vector( 5 downto 0);
Q_TX : out std_logic);
end io;
architecture Behavioral of io is
component uart
generic(CLOCK_FREQ : std_logic_vector(31 downto 0);
BAUD_RATE : std_logic_vector(27 downto 0));
port( I_CLK : in std_logic;
I_CLR : in std_logic;
I_RD : in std_logic;
I_WE : in std_logic;
I_RX : in std_logic;
I_TX_DATA : in std_logic_vector(7 downto 0);
Q_RX_DATA : out std_logic_vector(7 downto 0);
Q_RX_READY : out std_logic;
Q_TX : out std_logic;
Q_TX_BUSY : out std_logic);
end component;
component sc_corproc is
port(
clk : in std_logic;
ena : in std_logic;
Ain : in std_logic_vector(15 downto 0);
sin : out std_logic_vector(15 downto 0);
cos : out std_logic_vector(15 downto 0));
end component sc_corproc;
signal U_RX_READY : std_logic;
signal U_TX_BUSY : std_logic;
signal U_RX_DATA : std_logic_vector( 7 downto 0);
signal Angle_LSB, Angle_MSB : std_logic_vector( 7 downto 0); --CORDIC inputs
--signal s_Ain,s_sin,s_cos : signed(15 downto 0);
signal sinLSB, sinMSB : std_logic_vector( 7 downto 0); --CORDIC outputs
signal cosLSB, cosMSB : std_logic_vector( 7 downto 0); --CORDIC outputs
signal L_INTVEC : std_logic_vector( 5 downto 0);
signal L_LEDS : std_logic;
signal L_RD_UART : std_logic;
signal L_RX_INT_ENABLED : std_logic;
signal L_TX_INT_ENABLED : std_logic;
signal L_WE_UART : std_logic;
signal Ena : std_logic; -- CORDIC start
--> added 2011/10/19
signal baud_clk : std_logic;
--<
begin
urt: uart
generic map(CLOCK_FREQ => std_logic_vector(conv_unsigned(25000000, 32)),
BAUD_RATE => std_logic_vector(conv_unsigned( 38400, 28)))
port map( I_CLK => I_CLK, --baud_clk,--
I_CLR => I_CLR,
I_RD => L_RD_UART,
I_WE => L_WE_UART,
I_TX_DATA => I_DIN(7 downto 0),
I_RX => I_RX,
Q_TX => Q_TX,
Q_RX_DATA => U_RX_DATA,
Q_RX_READY => U_RX_READY,
Q_TX_BUSY => U_TX_BUSY);
--> added 2011/10/19
baud_process: process(I_CLK) begin
if rising_edge(I_CLK) then
baud_clk <= not baud_clk;
end if;
end process;
--<
cordic: sc_corproc port map (
clk => I_CLK, --25MHz !!!!
ena => Ena,
Ain(15 downto 8)=> Angle_MSB,
Ain(7 downto 0) => Angle_LSB,
-- Ain => s_Ain,
sin(15 downto 8) => sinMSB,
sin(7 downto 0) => sinLSB,
-- sin => s_sin,
cos(15 downto 8) => cosMSB,
cos(7 downto 0) => cosLSB
-- cos => s_cos
);
-- IO read process
--
iord: process(I_ADR_IO, U_RX_DATA, U_RX_READY, L_RX_INT_ENABLED,
U_TX_BUSY, L_TX_INT_ENABLED,
sinMSB,sinLSB,cosMSB,cosLSB)
begin
-- addresses for mega8 device (use iom8.h or #define __AVR_ATmega8__).
--
case I_ADR_IO is
when X"2A" => Q_DOUT <= -- UCSRB:
L_RX_INT_ENABLED -- Rx complete int enabled.
& L_TX_INT_ENABLED -- Tx complete int enabled.
& L_TX_INT_ENABLED -- Tx empty int enabled.
& '1' -- Rx enabled
& '1' -- Tx enabled
& '0' -- 8 bits/char
& '0' -- Rx bit 8
& '0'; -- Tx bit 8
when X"2B" => Q_DOUT <= -- UCSRA:
U_RX_READY -- Rx complete
& not U_TX_BUSY -- Tx complete
& not U_TX_BUSY -- Tx ready
& '0' -- frame error
& '0' -- data overrun
& '0' -- parity error
& '0' -- double dpeed
& '0'; -- multiproc mode
when X"2C" => Q_DOUT <= U_RX_DATA; -- UDR
when X"40" => Q_DOUT <= -- UCSRC
'1' -- URSEL
& '0' -- asynchronous
& "00" -- no parity
& '1' -- two stop bits
& "11" -- 8 bits/char
& '0'; -- rising clock edge
-- CORDIC outputs as processor inputs:
when X"36" => Q_DOUT <= sinMSB; -- PINB
when X"39" => Q_DOUT <= sinLSB; -- PINA
when X"30" => Q_DOUT <= cosMSB; -- PIND
when X"33" => Q_DOUT <= cosLSB; -- PINC
when others => Q_DOUT <= X"AA";
end case;
end process;
-- IO write process
--
iowr: process(I_CLK)
begin
if (rising_edge(I_CLK)) then
if (I_CLR = '1') then
L_RX_INT_ENABLED <= '0';
L_TX_INT_ENABLED <= '0';
elsif (I_WE_IO = '1') then
case I_ADR_IO is
when X"38" => -- PORTB
Angle_LSB <= I_DIN;
when X"35" => -- PORTC
Angle_MSB <= I_DIN;
when X"32" => -- PORTD
Ena <= I_DIN(0); --Ena en poids faible
when X"2A" => -- UCSRB
L_RX_INT_ENABLED <= I_DIN(7);
L_TX_INT_ENABLED <= I_DIN(6);
when X"2B" => -- UCSRA: handled by uart
when X"2C" => -- UDR: handled by uart
when X"40" => -- UCSRC/UBRRH: (ignored)
when others =>
end case;
end if;
end if;
end process;
-- interrupt process
--
ioint: process(I_CLK)
begin
if (rising_edge(I_CLK)) then
if (I_CLR = '1') then
L_INTVEC <= "000000";
else
case L_INTVEC is
-- vector 12 ??
when "101011" => -- vector 11 interrupt pending.
if (L_RX_INT_ENABLED and U_RX_READY) = '0' then
L_INTVEC <= "000000";
end if;
-- vector 14 ??
when "101100" => -- vector 12 interrupt pending.
if (L_TX_INT_ENABLED and not U_TX_BUSY) = '0' then
L_INTVEC <= "000000";
end if;
when others =>
-- no interrupt is pending.
-- We accept a new interrupt.
--
if (L_RX_INT_ENABLED and U_RX_READY) = '1' then
L_INTVEC <= "101011"; -- _VECTOR(11)
elsif (L_TX_INT_ENABLED and not U_TX_BUSY) = '1' then
L_INTVEC <= "101100"; -- _VECTOR(12)
else
L_INTVEC <= "000000"; -- no interrupt
end if;
end case;
end if;
end if;
end process;
L_WE_UART <= I_WE_IO when (I_ADR_IO = X"2C") else '0'; -- write UART UDR
L_RD_UART <= I_RD_IO when (I_ADR_IO = X"2C") else '0'; -- read UART UDR
Q_INTVEC <= L_INTVEC;
end Behavioral;
Une remarque pour terminer.
Le coprocesseur utilisé dans cette section est le coprocesseur pipeline. Ce genre de coprocesseur est peu adapté à ce que nous venons de faire. En effet il calcule sans arrêt à partir d'un signal de validation "Ena" mais ne donne jamais l'information "calcul réalisé" puisque le calcul ne s'arrête pas. Donc son principe d'utilisation est :
- positionnement du poids faible de l'angle
- positionnement du poids fort de l'angle
- positionnement du "Ena"
- attente 14 fronts d'horloge
- lecture du sinus
- lecture du cosinus
- positionnement de "Ena" à 0
Le contenu de cette remarque sera pris en compte lors des exercices complémentaires.
Quelques utilitaires pour tester
[modifier | modifier le wikicode]Le coprocesseur CORDIC fournit un calcul à l'ATMega et c’est ce dernier qui est chargé de le donner à l'extérieur pour tester. Le meilleurs moyen de réaliser tout cela est d’utiliser la liaison série. On entre l'angle sur lequel on veut faire le calcul dans un hyperterminal, le calcul se fait et le résultat s'affiche sur l'écran de l'hyperterminal. Mais pour faire cela il faut transformer la chaîne fournie par l'hyperterminal en format Q3.13 et inversement, le résultat Q3.13 devra être converti en chaîne de caractères avant d’être envoyé. Pour faciliter ces conversions, nous proposons quelques utilitaires regroupés ci-dessous :
//************************************************************************
// function HexQ3_13ToFloat_AVR()
// purpose: transformation of a 16-bit Q3.13 number into 32-bit float number
// arguments:
// corresponding Q3.13 number
// return: 32-bit float
// note: This function works on Arduino Mega 2560 but only with hardcoded
// parameters in my core at the moment
// use the code below for a check
//************************************************************************
float HexQ3_13ToFloat_AVR(int val){
union {
float f_temp; //taille : {{unité|4|octets}}
long int li_temp; //taille : {{unité|4|octets}}
} u;
long int i_temp;
unsigned char exposant=129;//,*p;
signed char i;
if (val < 0) i_temp = -val; else i_temp = val;
for (i=15;i>=0;i--) {
if (i_temp & (1<<i)) {
// on efface le '1' trouvé :
i_temp= i_temp & ~(1<<i);
break;// on sort de la boucle
}
exposant--;
}
u.li_temp = exposant;
u.li_temp <<=23;
u.li_temp = u.li_temp|(i_temp << (23-i));
if (val < 0)
u.f_temp = -u.f_temp;//-u.f_temp;
return u.f_temp;
}
//************************************************************************
// function float2HexQ3_13()
// purpose: transformation of a 32-bit float number into Q3.13
// arguments:
// corresponding float number and the returned string
// return: integer in Q3.13 format
// note:
//************************************************************************
int float2HexQ3_13(float val){ //conversion float vers Q3.13
int temp;
char i;
float f_temp;
if (val < 0) f_temp = -val; else f_temp = val;
temp = ((int) floor(f_temp)<<13);
f_temp = f_temp - floor(f_temp);
for (i=0;i<13;i++) {
temp|=((int)floor(2*f_temp)<<(12-i));
f_temp = 2*f_temp - floor(2*f_temp);
}
if (val < 0) return -temp; else return temp;
}
//************************************************************************
// function float2HexQ3_13_AVR()
// purpose: transformation of a 32-bit float number into Q3.13
// arguments:
// corresponding float number and the returned string
// return: integer in Q3.13 format
// note: idem to float2HexQ3_13 but without float library
// utilise {{unité|500|octets}} de moins que la précédente
// Fonctionne pour paramètre en dur sur notre cœur
// Fonctionne parfaitement sur un Arduino
//************************************************************************
int float2HexQ3_13_AVR(float val){ //conversion float vers Q3.13
union {
float f_temp; //taille : {{unité|4|octets}}
long int li_temp; //taille : {{unité|4|octets}}
} u,v;
unsigned char exposant;
unsigned long int mantisse;
int result=0;
u.f_temp = val;
if (val < 0) u.f_temp = - u.f_temp;
v = u;
// recupération de l'exposant
v.li_temp >>= 23;
exposant = v.li_temp;
// recuperation mantisse
if (exposant < 129) {
mantisse = (u.li_temp & 0X007FFFFF);
// mise à 1 du bit manquant
result |= (1 << (exposant-114)); // (15-129+exposant)); semble OK
mantisse >>= (137-exposant); //(22-(14-129+exposant));
result |= mantisse;
if (val < 0) return -result;
else return result;
} else {
//**** "Erreur conversion"*****
usart_puts("Erreur conversion : nombre trop grand\n");
return 0x7FFF; // le plus grand que l’on puisse faire en Q3.13
}
}
//************************************************************************
// function HexQ3_13ToString()
// purpose: transformation of a Q3.13 number into string
// arguments:
// corresponding Q3.13 number and the returned string
// return:
// note: only four decimal digit of too lengthy numbers are calculated !!
//************************************************************************
void HexQ3_13ToString(int valQ3_13,char str[]){
unsigned int valQ3_13b;
char digit;
if (valQ3_13 < 0) { // eviter problèmes de signe !!!
str[0] = '-';
valQ3_13 = -valQ3_13;
} else
str[0] = '+';
digit = valQ3_13 >> 13;
str[1]= digit + '0';
str[2]= '.';
valQ3_13 &= 0x1FFF; // on retire les 3 bits de poids fort
valQ3_13 = valQ3_13 * 5; // *5 pour tenir dans 16 bits
valQ3_13b = valQ3_13;
valQ3_13b >>= 12; // on ne garde que les 4 bits de poids fort
str[3] = valQ3_13b +'0';
valQ3_13 &= 0x0FFF; // on retire les 4 bits de poids fort
valQ3_13 = valQ3_13 * 10; //enfin le *10
valQ3_13b = valQ3_13;
valQ3_13b >>= 12; // on ne garde que les 4 bits de poids fort
str[4] = valQ3_13b +'0';
valQ3_13 &= 0x0FFF; // on retire les 4 bits de poids fort
valQ3_13 = valQ3_13 * 10;
valQ3_13b = valQ3_13;
valQ3_13b >>= 12; // on ne garde que les 4 bits de poids fort
str[5] = valQ3_13b +'0';
valQ3_13 &= 0x0FFF; // on retire les 4 bits de poids fort
valQ3_13 = valQ3_13 * 10;
valQ3_13b = valQ3_13;
valQ3_13b >>= 12; // on ne garde que les 4 bits de poids fort
str[6] = valQ3_13b +'0';
str[7]=0;
}
//************************************************************************
// function StringToQ3_13()
// purpose: transformation of string in a number in a Q3.13 format
// only +x.xxxx and -x.xxxx are correct
// arguments:
// corresponding string
// return: number in a fixed-point Q3.13 format
// note: only four decimal digit of too lengthy numbers are used !!
//************************************************************************
int StringToQ3_13(char str[]){
uint8_t i=0;
int var=0;
int valq3_13=0;
valq3_13=(str[1]-'0')<<13; // partie entiere dans le 2ieme bit
// partie decimale sous forme d'un entier ( 0,5312 => 5312)
var=(str[3]-'0')*1000 +(str[4]-'0')*100 +(str[5]-'0')*10 +(str[6]-'0');
// comparaison avec les puissances de -i (0,5 0,25 0,125 0,0625 ...) soit en entier 5000 2500 1250 625 ...
for(i=0;i<13;i++) {
// remplissage des bit correspondants a 0 ou 1 selon comparaison et soustraction le cas échéant du poids rencontré
if (var>=(5000>>i)) {
valq3_13 = valq3_13 | (1<<(12-i));
var=var-(5000>>i);
}
}
// test le signe pour envoi du nombre ou de son opposé
if (str[0]=='+')
return valq3_13;
else
return -valq3_13;
}
//************************************************************************
// function check_syntaxe()
// purpose: check syntaxe of numbers :
// only +x.xxxx and -x.xxxx are correct
// arguments:
// corresponding string where characters lie
// return: true or false
// note: numbers too lengthy are considered as good numbers !!!
//************************************************************************
uint8_t check_syntaxe(char str[]) {
uint8_t i=3, result=0;
if ((str[0]=='+')||(str[0]=='-')) result++;
if ((str[1]=='0')||(str[1]=='1')) result++;
if (str[2]=='.') result++;
do {
if ((str[i]<='9') && (str[i]>='0')) result++;
i++;
} while(str[i]!=0);
if (result>=7) return 1; else return 0;
}
//************************************************************************
// function usart_gets()
// purpose: gets characters in first rs232 PORT
// arguments:
// corresponding string where characters are put
// return: corresponding string where characters are put
// note: 38400,8,n,2 hard coded : transmission
// initialisation uart prealable requise
//************************************************************************
void usart_gets(char str[]) {
uint8_t i=0;
do {
str[i]=usart_receive();
i++;
} while(str[i-1]!=0x0D); // carriage return ?
str[i-1]=0;//end of string
}
//************************************************************************
// function usart_puts()
// purpose: puts characters in first rs232 PORT
// arguments:
// corresponding string
// return:
// note: 38400,8,n,2 hard coded : transmission
// initialisation uart prealable requise
//************************************************************************
void usart_puts(char str[]){
uint8_t i=0;
do {
usart_send(str[i]);
i++;
} while(str[i]!=0);
}
//************************************************************************
// function usart_puts_hexa()
// purpose: puts number in hexadecimel in first rs232 PORT
// arguments:
// corresponding number
// return:
// note: 38400,8,n,2 hard coded : transmission
// initialisation uart prealable requise
// only for 16-bit numbers and then Q3.13 numbers
//************************************************************************
void usart_puts_hexa(int nbQ3_13){
int8_t i=0,digit=0;
char char_digit;
usart_send('0');usart_send('X');
for (i=12;i>-1;i-=4) {// only four digits
digit = (nbQ3_13 >> i) & 0x0F;
char_digit=digit+0x30;
if (char_digit>0x39) char_digit += 7;
usart_send(char_digit);
}
}
//************************************************************************
// function usart_init()
// purpose: init first rs232 PORT
// arguments:
// no argument
// return:
// note: 38400,8,n,2 hard coded : transmission and reception
//************************************************************************
void usart_init(void) {
UCSRB = (1<<TXEN)|((1<<RXEN)); // transmission et reception
}
//************************************************************************
// function uart_send()
// purpose: put character in first rs232 PORT
// arguments:
// corresponding character
// return:
// note: 38400,8,n,2 hard coded
// initialisation uart prealable requise
//************************************************************************
void usart_send(unsigned char ch){
while(!(UCSRA & (1<<UDRE)));
UDR = ch;
}
//************************************************************************
// function uart_receive()
// purpose: read character in second rs232 PORT
// arguments:
// corresponding character
// return: blocking sub return char
// note: 38400,8,n,2 hard coded, non-blocking sub return 0 if no data present
// initialisation uart prealable requise
//************************************************************************
char usart_receive(void){
while (!(UCSRA & (1<<RXC))); //attente tant que Data Present en réception
return UDR;
}
Si ces utilitaires ne fonctionnent pas cela peut être dû à un problème dans la vitesse de transmission. Toutes ces routines sont commentées pour 38400 bauds mais peuvent fonctionner à des vitesses doubles ou moitié selon votre horloge système !
Un programme principal pour tester
[modifier | modifier le wikicode]On donne un exemple partiel de programme principal pour tester :
do {
nbOK=0;
// on boucle tant que la syntaxe n’est pas bonne
do {
usart_puts("Entrez un nombre au format +x.xxxx ou -x.xxxx");
usart_send(0X0D);usart_send(0X0A);
usart_gets(chaine);
nbOK=check_syntaxe(chaine);
if (!nbOK) {
usart_puts("!!!! Mauvais nombre !!!!");
usart_send(0X0D);usart_send(0X0A);
}
} while(!nbOK);
// verification visuelle de saisie correcte :
beta = StringToQ3_13(chaine);
usart_puts("beta=");
HexQ3_13ToString(beta,chaine);
usart_puts(chaine);
usart_send(0X0D);usart_send(0X0A);
// fin verification visuelle
// saisie de l'angle dans les deux PORTs
PORTB = beta; //
PORTC = beta>>8;
PORTD = 1; // start
// attente obligatoire du calcul :
_delay_ms(50);
x = PINB;
x <<=8; // poussé dans poids forts
x += PINA;
y = PIND;
y <<= 8; // poussé dans poids forts
y += PINC;
// Affichage du résultat
HexQ3_13ToString(x,chaine);
usart_puts(chaine);
usart_send('=');usart_puts_hexa(x);
usart_send(' ');usart_send(' ');usart_send(' ');
HexQ3_13ToString(y,chaine);
usart_puts(chaine);usart_send('=');usart_puts_hexa(y);
usart_send(0x0D);usart_send(0x0A);
_delay_ms(500);
} while(1);
Nous allons proposer quelques exercices matériels pour ceux qui veulent aller plus loin.
Quelques idées pour des exercices complémentaires
[modifier | modifier le wikicode]Nous allons présenter dans cette section un ensemble d'exercices pour aller plus loin avec CORDIC sur une petite architecture 8 bits. Certains de ces exercices ont été réalisés mais pas d'autres. Nous les laissons pour les étudiants ou enseignants qui désirent aller plus loin.
Transformer le cœur pipeline en périphérique
[modifier | modifier le wikicode]Le cœur pipeline du CORDIC que nous avons donné plus haut est assez mal adapté à la notion de périphérique. Il est en effet trop indépendant du processeur. Traditionnellement les périphériques sont configurables par des registres, et un drapeau indique la fin du travail. Ce bit peut d'ailleurs, en général, être utilisé pour déclencher une interruption...
Un pipeline est, quant à lui, destiné à traiter des informations au fur et à mesure. D'une certaine manière, il ne termine jamais son travail. Notre problème va donc consister à le transformer en un périphérique digne de ce nom.
Ajouter un fonctionnement correct de l'entrée "ena"
[modifier | modifier le wikicode]L'entrée "ena" présente dans l'entité du cœur CORDIC ne sert absolument à rien. Vous allez transformer le fichier "cordic2.vhd" pour la rendre utile : s'il elle n’est pas à '1' le cœur ne calcule pas. Fonctionnement assez traditionnelle pour ce type d'entrée.
L'utilisation d'un tel cœur consistera alors à :
- positionner l'angle en écrivant dans deux PORTs
- positionner "ena" à 1 pour lancer le calcul.
- perdre un peu de temps et repositionner "ena" à 0
- lire les sinus et cosinus
Ce qui nous déplait dans cette façon de faire est l'attente par perte de temps. À ce stade, il n'y a pas grand chose d'amélioré par rapport au cœur d'origine, sauf la possibilité de l'arrêter. Nous allons améliorer cela mais nous vous conseillons de réaliser cette étape et de la tester.
Ajouter une détection de la fin de calcul
[modifier | modifier le wikicode]Un bit de sortie sera prévu pour détecter la terminaison du calcul. Ce travail n’est pas difficile à faire. Il s'agit d'ajouter un compteur dans CORDIC sur 4 bits qui s'incrémente aussi avec "ena" (et l'horloge bien sûr). Quand le compteur est à une certaine valeur (14 pour nous) et bien on positionne un bit (appelé "done") à 1 (et l’on pourrait automatiquement positionner "ena" à 0 mais cette option ne sera pas choisie).
L'utilisation d'un tel cœur consistera alors à :
- positionner l'angle en écrivant dans deux PORTs
- positionner "ena" à 1 pour lancer le calcul.
- Attendre le positionnement du bit "done" (de fin de calcul) et repositionner "ena" à 0 (avec le processeur)
- lire les sinus et cosinus
La façon d'organiser tout cela peut se faire avec quelques petites variations :
- le repositionnement de "ena" à 0 peut se faire de manière automatique quand on lit un des registres de résultat
- le repositionnement de "ena" à 0 peut se faire automatiquement par la détection de la fin des calculs (ce n’est pas le processeur qui le fait)
- le deuxième choix peut même amener à retirer le bit fin de calcul : c’est "ena" qui sert à tout : on le positionne à '1' et on attend qu’il repasse à 0
Et voici donc une correction partielle correspondant aux deux versions améliorées proposées ci-dessus :
- Ajouter un fonctionnement correct de l'entrée "ena"
- Ajouter une détection de la fin de calcul
D'abord la connexion du registre PORTD responsable du positionnement de "ena" (en poids faible) :
-- IO write process
--
iowr: process(I_CLK)
begin
if (rising_edge(I_CLK)) then
if (I_CLR = '1') then
L_RX_INT_ENABLED <= '0';
L_TX_INT_ENABLED <= '0';
elsif (I_WE_IO = '1') then
case I_ADR_IO is
when X"38" => -- PORTB
Angle_LSB <= I_DIN;
when X"35" => -- PORTC
Angle_MSB <= I_DIN;
when X"32" => -- PORTD
Ena <= I_DIN(0); --Ena en poids faible du PORTD
when X"2A" => -- UCSRB
L_RX_INT_ENABLED <= I_DIN(7);
L_TX_INT_ENABLED <= I_DIN(6);
when X"2B" => -- UCSRA: handled by uart
when X"2C" => -- UDR: handled by uart
when X"40" => -- UCSRC/UBRRH: (ignored)
when others =>
end case;
end if;
end if;
end process;
Ensuite la lecture de l'état du calcul avec encore le PORTD :
iord: process(I_ADR_IO, U_RX_DATA, U_RX_READY, L_RX_INT_ENABLED,
U_TX_BUSY, L_TX_INT_ENABLED,sinMSB,sinLSB,cosMSB,cosLSB)
begin
-- addresses for mega8 device (use iom8.h or #define __AVR_ATmega8__).
--
case I_ADR_IO is
when X"2A" => Q_DOUT <= -- UCSRB:
L_RX_INT_ENABLED -- Rx complete int enabled.
& L_TX_INT_ENABLED -- Tx complete int enabled.
& L_TX_INT_ENABLED -- Tx empty int enabled.
& '1' -- Rx enabled
& '1' -- Tx enabled
& '0' -- 8 bits/char
& '0' -- Rx bit 8
& '0'; -- Tx bit 8
when X"2B" => Q_DOUT <= -- UCSRA:
U_RX_READY -- Rx complete
& not U_TX_BUSY -- Tx complete
& not U_TX_BUSY -- Tx ready
& '0' -- frame error
& '0' -- data overrun
& '0' -- parity error
& '0' -- double dpeed
& '0'; -- multiproc mode
when X"2C" => Q_DOUT <= U_RX_DATA; -- UDR
when X"40" => Q_DOUT <= -- UCSRC
'1' -- URSEL
& '0' -- asynchronous
& "00" -- no parity
& '1' -- two stop bits
& "11" -- 8 bits/char
& '0'; -- rising clock edge
-- CORDIC outputs as processor inputs:
when X"36" => Q_DOUT <= sinMSB; -- PINB
when X"39" => Q_DOUT <= sinLSB; -- PINA
when X"30" => Q_DOUT <= cosMSB; -- PIND
when X"33" => Q_DOUT <= cosLSB; -- PINC
-- exo 4-2
when X"32" => Q_DOUT(1) <= s_done; -- PORTD
Q_DOUT(0) <= Ena;
when others => Q_DOUT <= X"AA";
end case;
end process;
Ensuite le cœur CORDIC modifié
library ieee;
use ieee.std_logic_1164.all;
use ieee.std_logic_arith.all;
use IEEE.STD_LOGIC_UNSIGNED.ALL;
--USE ieee.numeric_std.all;
entity sc_corproc is
port(
clk : in std_logic;
ena : in std_logic;
Ain : in std_logic_vector(15 downto 0);
done : out std_logic;
sin : out std_logic_vector(15 downto 0);
cos : out std_logic_vector(15 downto 0));
end entity sc_corproc;
--ARCHITECTURE rtl OF sc_corproc IS
--BEGIN
-- PROCESS(clk) BEGIN
-- IF rising_edge(clk) THEN
-- cos <= Ain;
-- sin <= Ain+1;
-- END IF;
-- END PROCESS;
--END rtl;
ARCHITECTURE rtl OF sc_corproc IS
-- TYPE signed_array IS signed(15 DOWNTO 0);
SIGNAL x_array : std_logic_vector(15 DOWNTO 0);--signed_array;-- := (OTHERS =>'0');
SIGNAL y_array : std_logic_vector(15 DOWNTO 0);--signed_array;-- := (OTHERS =>'0');
SIGNAL z_array : std_logic_vector(15 DOWNTO 0);--signed_array;-- := (OTHERS =>'0');
SIGNAL x_array_1 : std_logic_vector(15 DOWNTO 0);--signed_array;-- := (OTHERS =>'0');
SIGNAL y_array_1 : std_logic_vector(15 DOWNTO 0);--signed_array;-- := (OTHERS =>'0');
SIGNAL z_array_1 : std_logic_vector(15 DOWNTO 0);
SIGNAL x_array_2 : std_logic_vector(15 DOWNTO 0);--signed_array;-- := (OTHERS =>'0');
SIGNAL y_array_2 : std_logic_vector(15 DOWNTO 0);--signed_array;-- := (OTHERS =>'0');
SIGNAL z_array_2 : std_logic_vector(15 DOWNTO 0);
SIGNAL x_array_3 : std_logic_vector(15 DOWNTO 0);--signed_array;-- := (OTHERS =>'0');
SIGNAL y_array_3 : std_logic_vector(15 DOWNTO 0);--signed_array;-- := (OTHERS =>'0');
SIGNAL z_array_3 : std_logic_vector(15 DOWNTO 0);
SIGNAL x_array_4 : std_logic_vector(15 DOWNTO 0);--signed_array;-- := (OTHERS =>'0');
SIGNAL y_array_4 : std_logic_vector(15 DOWNTO 0);--signed_array;-- := (OTHERS =>'0');
SIGNAL z_array_4 : std_logic_vector(15 DOWNTO 0);
SIGNAL x_array_5 : std_logic_vector(15 DOWNTO 0);--signed_array;-- := (OTHERS =>'0');
SIGNAL y_array_5 : std_logic_vector(15 DOWNTO 0);--signed_array;-- := (OTHERS =>'0');
SIGNAL z_array_5 : std_logic_vector(15 DOWNTO 0);
SIGNAL x_array_6 : std_logic_vector(15 DOWNTO 0);--signed_array;-- := (OTHERS =>'0');
SIGNAL y_array_6 : std_logic_vector(15 DOWNTO 0);--signed_array;-- := (OTHERS =>'0');
SIGNAL z_array_6 : std_logic_vector(15 DOWNTO 0);
SIGNAL x_array_7 : std_logic_vector(15 DOWNTO 0);--signed_array;-- := (OTHERS =>'0');
SIGNAL y_array_7 : std_logic_vector(15 DOWNTO 0);--signed_array;-- := (OTHERS =>'0');
SIGNAL z_array_7 : std_logic_vector(15 DOWNTO 0);
SIGNAL x_array_8 : std_logic_vector(15 DOWNTO 0);--signed_array;-- := (OTHERS =>'0');
SIGNAL y_array_8 : std_logic_vector(15 DOWNTO 0);--signed_array;-- := (OTHERS =>'0');
SIGNAL z_array_8 : std_logic_vector(15 DOWNTO 0);
SIGNAL x_array_9 : std_logic_vector(15 DOWNTO 0);--signed_array;-- := (OTHERS =>'0');
SIGNAL y_array_9 : std_logic_vector(15 DOWNTO 0);--signed_array;-- := (OTHERS =>'0');
SIGNAL z_array_9 : std_logic_vector(15 DOWNTO 0);
SIGNAL x_array_10 : std_logic_vector(15 DOWNTO 0);--signed_array;-- := (OTHERS =>'0');
SIGNAL y_array_10 : std_logic_vector(15 DOWNTO 0);--signed_array;-- := (OTHERS =>'0');
SIGNAL z_array_10 : std_logic_vector(15 DOWNTO 0);
SIGNAL x_array_11 : std_logic_vector(15 DOWNTO 0);--signed_array;-- := (OTHERS =>'0');
SIGNAL y_array_11 : std_logic_vector(15 DOWNTO 0);--signed_array;-- := (OTHERS =>'0');
SIGNAL z_array_11 : std_logic_vector(15 DOWNTO 0);
SIGNAL x_array_12 : std_logic_vector(15 DOWNTO 0);--signed_array;-- := (OTHERS =>'0');
SIGNAL y_array_12 : std_logic_vector(15 DOWNTO 0);--signed_array;-- := (OTHERS =>'0');
SIGNAL z_array_12 : std_logic_vector(15 DOWNTO 0);
SIGNAL x_array_13 : std_logic_vector(15 DOWNTO 0);--signed_array;-- := (OTHERS =>'0');
SIGNAL y_array_13 : std_logic_vector(15 DOWNTO 0);--signed_array;-- := (OTHERS =>'0');
SIGNAL z_ip : std_logic_vector(15 DOWNTO 0);
SIGNAL x_ip : std_logic_vector(15 DOWNTO 0);
SIGNAL y_ip : std_logic_vector(15 DOWNTO 0);
-- compteur pour signal done
SIGNAL cmpt :std_logic_vector(3 DOWNTO 0);
BEGIN
-- compteur de gestion du signal done
process(clk) begin
if rising_edge(clk) then
if ena ='1' then
if cmpt < 14 then
cmpt <= cmpt + 1;
else
cmpt <= x"E";
end if;
else
cmpt <=x"0";
end if;
end if;
end process;
-- gestion done CORDIC
process(cmpt) begin
if cmpt = x"E" then
done <= '1';
else
done <= '0';
end if;
end process;
--CORDIC proprement dit
PROCESS(clk)
BEGIN
IF rising_edge(clk) THEN
IF ena = '0' THEN
x_ip <= x"136F"; -- = 0.6073 en format Q3.13 ;
z_ip <= (OTHERS => '0');
y_ip <= (OTHERS => '0');
ELSE
IF Ain(15) = '1' THEN
x_array <= (x_ip) + (y_ip);
y_array <= (y_ip) - (x_ip);
-- x_array <= x"136F";
-- y_array <= 0 - x"136F";
z_array <= (Ain) + x"1921";--tan_array(0);
ELSE
x_array <= x"136F";
y_array <= x"136F";
z_array <= (Ain) - x"1921";--tan_array(0);
-- z_array <= x"2181"- x"1921";--tan_array(0);
END IF;
IF z_array(15) = '1' THEN
x_array_1 <= x_array + (y_array(15) & y_array(15 downto 1));
y_array_1 <= y_array - (x_array(15) & x_array(15 downto 1));
z_array_1 <= z_array + x"0ED6";
ELSE
x_array_1 <= x_array - (y_array(15) & y_array(15 downto 1));
y_array_1 <= y_array + (x_array(15) & x_array(15 downto 1));
z_array_1 <= z_array - x"0ED6";
END IF;
IF z_array_1(15) = '1' THEN
x_array_2 <= x_array_1 + (y_array_1(15) & y_array_1(15) & y_array_1(15 downto 2));
y_array_2 <= y_array_1 - (x_array_1(15) & x_array_1(15) & x_array_1(15 downto 2));
z_array_2 <= z_array_1 + x"07D6";
ELSE
x_array_2 <= x_array_1 - (y_array_1(15) & y_array_1(15) & y_array_1(15 downto 2));
y_array_2 <= y_array_1 + (x_array_1(15) & x_array_1(15) & x_array_1(15 downto 2));
z_array_2 <= z_array_1 - x"07D6";
END IF;
IF z_array_2(15) = '1' THEN
x_array_3 <= x_array_2 + (y_array_2(15) & y_array_2(15) & y_array_2(15) & y_array_2(15 downto 3));
y_array_3 <= y_array_2 - (x_array_2(15) & x_array_2(15) & x_array_2(15) & x_array_2(15 downto 3));
z_array_3 <= z_array_2 + x"03FA";
ELSE
x_array_3 <= x_array_2 - (y_array_2(15) & y_array_2(15) & y_array_2(15) & y_array_2(15 downto 3));
y_array_3 <= y_array_2 + (x_array_2(15) & x_array_2(15) & x_array_2(15) & x_array_2(15 downto 3));
z_array_3 <= z_array_2 - x"03FA";
END IF;
IF z_array_3(15) = '1' THEN
x_array_4 <= x_array_3 + (y_array_3(15) & y_array_3(15) & y_array_3(15) &
y_array_3(15) & y_array_3(15 downto 4));
y_array_4 <= y_array_3 - (x_array_3(15) & x_array_3(15) & x_array_3(15) &
x_array_3(15) & x_array_3(15 downto 4));
z_array_4 <= z_array_3 + x"01FF";
ELSE
x_array_4 <= x_array_3 - (y_array_3(15) & y_array_3(15) & y_array_3(15) &
y_array_3(15) & y_array_3(15 downto 4));
y_array_4 <= y_array_3 + (x_array_3(15) & x_array_3(15) & x_array_3(15) &
x_array_3(15) & x_array_3(15 downto 4));
z_array_4 <= z_array_3 - x"01FF";
END IF;
IF z_array_4(15) = '1' THEN
x_array_5 <= x_array_4 + (y_array_4(15) & y_array_4(15) & y_array_4(15) &
y_array_4(15) & y_array_4(15) & y_array_4(15 downto 5));
y_array_5 <= y_array_4 - (x_array_4(15) & x_array_4(15) & x_array_4(15) &
x_array_4(15) & x_array_4(15) & x_array_4(15 downto 5));
z_array_5 <= z_array_4 + x"00FF";
ELSE
x_array_5 <= x_array_4 - (y_array_4(15) & y_array_4(15) & y_array_4(15) &
y_array_4(15) & y_array_4(15) & y_array_4(15 downto 5));
y_array_5 <= y_array_4 + (x_array_4(15) & x_array_4(15) & x_array_4(15) &
x_array_4(15) & x_array_4(15) & x_array_4(15 downto 5));
z_array_5 <= z_array_4 - x"00FF";
END IF;
IF z_array_5(15) = '1' THEN
x_array_6 <= x_array_5 + (y_array_5(15) & y_array_5(15) & y_array_5(15) &
--y_array_5(15) & y_array_5(15) & y_array_5(15) & y_array_5(15) & y_array_5(15 downto 6));
y_array_5(15) & y_array_5(15) & y_array_5(15) & y_array_5(15 downto 6));
y_array_6 <= y_array_5 - (x_array_5(15) & x_array_5(15) & x_array_5(15) &
--x_array_5(15) & x_array_5(15) & x_array_5(15) & x_array_5(15) & x_array_5(15 downto 6));
x_array_5(15) & x_array_5(15) & x_array_5(15) & x_array_5(15 downto 6));
z_array_6 <= z_array_5 + x"007F";
ELSE
x_array_6 <= x_array_5 - (y_array_5(15) & y_array_5(15) & y_array_5(15) &
y_array_5(15) & y_array_5(15) & y_array_5(15) & y_array_5(15 downto 6));
y_array_6 <= y_array_5 + (x_array_5(15) & x_array_5(15) & x_array_5(15) &
x_array_5(15) & x_array_5(15) & x_array_5(15) & x_array_5(15 downto 6));
z_array_6 <= z_array_5 - x"007F";
END IF;
IF z_array_6(15) = '1' THEN
x_array_7 <= x_array_6 + (y_array_6(15) & y_array_6(15) & y_array_6(15) &
y_array_6(15) & y_array_6(15) & y_array_6(15) & y_array_6(15) &
y_array_6(15 downto 7));
y_array_7 <= y_array_6 - (x_array_6(15) & x_array_6(15) & x_array_6(15) &
x_array_6(15) & x_array_6(15) & x_array_6(15) & x_array_6(15) &
x_array_6(15 downto 7));
z_array_7 <= z_array_6 + x"003F";
ELSE
x_array_7 <= x_array_6 - (y_array_6(15) & y_array_6(15) & y_array_6(15) &
y_array_6(15) & y_array_6(15) & y_array_6(15) & y_array_6(15) &
y_array_6(15 downto 7));
y_array_7 <= y_array_6 + (x_array_6(15) & x_array_6(15) & x_array_6(15) &
x_array_6(15) & x_array_6(15) & x_array_6(15) & x_array_6(15) &
x_array_6(15 downto 7));
z_array_7 <= z_array_6 - x"003F";
END IF;
IF z_array_7(15) = '1' THEN
x_array_8 <= x_array_7 + (y_array_7(15) & y_array_7(15) & y_array_7(15) &
y_array_7(15) & y_array_7(15) & y_array_7(15) & y_array_7(15) & y_array_7(15) &
y_array_7(15 downto 8));
y_array_8 <= y_array_7 - (x_array_7(15) & x_array_7(15) & x_array_7(15) &
x_array_7(15) & x_array_7(15) & x_array_7(15) & x_array_7(15) & x_array_7(15) &
x_array_7(15 downto 8));
z_array_8 <= z_array_7 + x"001F";
ELSE
x_array_8 <= x_array_7 - (y_array_7(15) & y_array_7(15) & y_array_7(15) &
y_array_7(15) & y_array_7(15) & y_array_7(15) & y_array_7(15) & y_array_7(15) &
y_array_7(15 downto 8));
y_array_8 <= y_array_7 + (x_array_7(15) & x_array_7(15) & x_array_7(15) &
x_array_7(15) & x_array_7(15) & x_array_7(15) & x_array_7(15) & x_array_7(15) &
x_array_7(15 downto 8));
z_array_8 <= z_array_7 - x"001F";
END IF;
IF z_array_8(15) = '1' THEN
x_array_9 <= x_array_8 + (y_array_8(15) & y_array_8(15) & y_array_8(15) &
y_array_8(15) & y_array_8(15) & y_array_8(15) & y_array_8(15) & y_array_8(15) &
y_array_8(15) & y_array_8(15 downto 9));
y_array_9 <= y_array_8 - (x_array_8(15) & x_array_8(15) & x_array_8(15) &
x_array_8(15) & x_array_8(15) & x_array_8(15) & x_array_8(15) & x_array_8(15) &
x_array_8(15) & x_array_8(15 downto 9));
z_array_9 <= z_array_8 + x"000F";
ELSE
x_array_9 <= x_array_8 - (y_array_8(15) & y_array_8(15) & y_array_8(15) &
y_array_8(15) & y_array_8(15) & y_array_8(15) & y_array_8(15) & y_array_8(15) &
y_array_8(15) & y_array_8(15 downto 9));
y_array_9 <= y_array_8 + (x_array_8(15) & x_array_8(15) & x_array_8(15) &
x_array_8(15) & x_array_8(15) & x_array_8(15) & x_array_8(15) & x_array_8(15) &
x_array_8(15) & x_array_8(15 downto 9));
z_array_9 <= z_array_8 - x"000F";
END IF;
IF z_array_9(15) = '1' THEN
x_array_10 <= x_array_9 + (y_array_9(15) & y_array_9(15) & y_array_9(15) &
y_array_9(15) & y_array_9(15) & y_array_9(15) & y_array_9(15) & y_array_9(15) &
y_array_9(15) & y_array_9(15) & y_array_9(15 downto 10));
y_array_10 <= y_array_9 - (x_array_9(15) & x_array_9(15) & x_array_9(15) &
x_array_9(15) & x_array_9(15) & x_array_9(15) & x_array_9(15) & x_array_9(15) &
x_array_9(15) & x_array_9(15) & x_array_9(15 downto 10));
z_array_10 <= z_array_9 + x"0007";
ELSE
x_array_10 <= x_array_9 - (y_array_9(15) & y_array_9(15) & y_array_9(15) &
y_array_9(15) & y_array_9(15) & y_array_9(15) & y_array_9(15) & y_array_9(15) &
y_array_9(15) & y_array_9(15) & y_array_9(15 downto 10));
y_array_10 <= y_array_9 + (x_array_9(15) & x_array_9(15) & x_array_9(15) &
x_array_9(15) & x_array_9(15) & x_array_9(15) & x_array_9(15) & x_array_9(15) &
x_array_9(15) & x_array_9(15) & x_array_9(15 downto 10));
z_array_10 <= z_array_9 - x"0007";
END IF;
IF z_array_10(15) = '1' THEN
x_array_11 <= x_array_10 + (y_array_10(15) & y_array_10(15) & y_array_10(15) &
y_array_10(15) & y_array_10(15) & y_array_10(15) & y_array_10(15) & y_array_10(15) &
y_array_10(15) & y_array_10(15) & y_array_10(15) & y_array_10(15 downto 11));
y_array_11 <= y_array_10 - (x_array_10(15) & x_array_10(15) & x_array_10(15) &
x_array_10(15) & x_array_10(15) & x_array_10(15) & x_array_10(15) & x_array_10(15) &
x_array_10(15) & x_array_10(15) & x_array_10(15) & x_array_10(15 downto 11));
z_array_11 <= z_array_10 + x"0003";
ELSE
x_array_11 <= x_array_10 - (y_array_10(15) & y_array_10(15) & y_array_10(15) &
y_array_10(15) & y_array_10(15) & y_array_10(15) & y_array_10(15) & y_array_10(15) &
y_array_10(15) & y_array_10(15) & y_array_10(15) & y_array_10(15 downto 11));
y_array_11 <= y_array_10 + (x_array_10(15) & x_array_10(15) & x_array_10(15) &
x_array_10(15) & x_array_10(15) & x_array_10(15) & x_array_10(15) & x_array_10(15) &
x_array_10(15) & x_array_10(15) & x_array_10(15) & x_array_10(15 downto 11));
z_array_11 <= z_array_10 - x"0003";
END IF;
IF z_array_11(15) = '1' THEN
x_array_12 <= x_array_11 + (y_array_11(15) & y_array_11(15) & y_array_11(15) & y_array_11(15) &
y_array_11(15) & y_array_11(15) & y_array_11(15) & y_array_11(15) & y_array_11(15) & y_array_11(15) &
y_array_11(15) & y_array_11(15) & y_array_11(15 downto 12));
y_array_12 <= y_array_11 - (x_array_11(15) & x_array_11(15) & x_array_11(15) &
x_array_11(15) & x_array_11(15) & x_array_11(15) & x_array_11(15) & x_array_11(15) & x_array_11(15) &
x_array_11(15) & x_array_11(15) & x_array_11(15 downto 12));
z_array_12 <= z_array_11 + x"0001";
ELSE
x_array_12 <= x_array_11 - (y_array_11(15) & y_array_11(15) & y_array_11(15) & y_array_11(15) &
y_array_11(15) & y_array_11(15) & y_array_11(15) & y_array_11(15) & y_array_11(15) & y_array_11(15) &
y_array_11(15) & y_array_11(15) & y_array_11(15 downto 12));
y_array_12 <= y_array_11 + (x_array_11(15) & x_array_11(15) & x_array_11(15) & x_array_11(15) &
x_array_11(15) & x_array_11(15) & x_array_11(15) & x_array_11(15) & x_array_11(15) & x_array_11(15) &
x_array_11(15) & x_array_11(15) & x_array_11(15 downto 12));
z_array_12 <= z_array_11 - x"0001";
END IF;
IF z_array_12(15) = '1' THEN
x_array_13 <= x_array_12 + (y_array_12(15) & y_array_12(15) & y_array_12(15) & y_array_12(15) &
y_array_12(15) & y_array_12(15) & y_array_12(15) & y_array_12(15) & y_array_12(15) & y_array_12(15) &
y_array_12(15) & y_array_12(15) & y_array_12(15) & y_array_12(15 downto 13));
y_array_13 <= y_array_12 - (x_array_12(15) & x_array_12(15) & x_array_12(15) & x_array_12(15) &
x_array_12(15) & x_array_12(15) & x_array_12(15) & x_array_12(15) & x_array_12(15) &
x_array_12(15) & x_array_12(15) & x_array_12(15) & x_array_12(15) & x_array_12(15 downto 13));
-- z_array_13 <= z_array_12 + x"0000";
ELSE
x_array_13 <= x_array_12 - (y_array_12(15) & y_array_12(15) & y_array_12(15) & y_array_12(15) &
y_array_12(15) & y_array_12(15) & y_array_12(15) & y_array_12(15) & y_array_12(15) & y_array_12(15) &
y_array_12(15) & y_array_12(15) & y_array_12(15) & y_array_12(15 downto 13));
y_array_13 <= y_array_12 + (x_array_12(15) & x_array_12(15) & x_array_12(15) & x_array_12(15) &
x_array_12(15) & x_array_12(15) & x_array_12(15) & x_array_12(15) & x_array_12(15) & x_array_12(15) &
x_array_12(15) & x_array_12(15) & x_array_12(15) & x_array_12(15 downto 13));
-- z_array_13 <= z_array_12 - x"0000";
END IF;
END IF;
END IF;
END PROCESS;
cos <= x_array_13;
sin <= y_array_13;
END rtl;
Et enfin les extraits du programme C utilisant ce cour CORDIC modifié
do {
nbOK=0;
// on boucle tant que la syntaxe n'est pas bonne
do {
usart_puts("Entrez un nombre au format +x.xxxx ou -x.xxxx");
usart_send(0X0D);usart_send(0X0A);
usart_gets(chaine);
nbOK=check_syntaxe(chaine);
if (!nbOK) {
usart_puts("!!!! Mauvais nombre !!!!");
usart_send(0X0D);usart_send(0X0A);
}
} while(!nbOK);
beta = StringToQ3_13(chaine);
usart_puts("beta=");
HexQ3_13ToString(beta,chaine);
usart_puts(chaine);
usart_send(0X0D);usart_send(0X0A);
// saisie de l'angle dans les deux PORTs
PORTB = beta; //
PORTC = beta>>8;
PORTD = 1; // core start
while((PORTD&0x02)==0);
PORTD = 0x00; // core stop et RAZ done
x = PINB;
x <<=8; // poussé dans poids forts
x += PINA;
y = PIND;
y <<= 8; // poussé dans poids forts
y += PINC;
// Affichage du résultat
HexQ3_13ToString(x,chaine);
usart_puts(chaine);
usart_send('=');usart_puts_hexa(x);
usart_send(' ');usart_send(' ');usart_send(' ');
HexQ3_13ToString(y,chaine);
usart_puts(chaine);usart_send('=');usart_puts_hexa(y);
usart_send(0x0D);usart_send(0x0A);
_delay_ms(500);
} while(1);
Remarquez que le matériel nécessite le passage du bit de poids faible à 0 avant un nouveau départ. Cette façon de faire pourrait être améliorée en utilisant un seul bit pour le départ et pour le done mais sa gestion se complique un peu.
Réalisation matérielle de la conversion virgule fixe vers virgule flottante
[modifier | modifier le wikicode]Cette conversion était l'objectif de la fonction donnée et déjà utilisée dans un exercice précédent :
float HexQ3_13ToFloat(int val)
Un coup d'œil sur le code source de cette fonction montre des calculs de puissance de deux en flottant et notre objectif ici est de les éliminer en laissant le matériel les réaliser. Pour ce faire, il est possible d’utiliser un cœur de calcul flottant, il en existe chez Opencores.org. Mais on va être plus subtil car notre conversion se fait dans un cas suffisamment simple et nous allons tenter une réalisation sans multiplication.
1°) Tester en C une conversion du type : Exposant = 129
Recherche du premier 1 dans le nombre Q3.13 en partant des poids forts et en décrémentant l'exposant.
Une fois trouvé supprimer ce 1, puis mettre l'exposant à sa place (E dans la figure ci-dessous) et mettre la mantisse (dans M) aussi à sa place.
On rappelle la documentation des nombres flottants :

| Encodage | Signe | Exposant | Mantisse | Valeur d'un nombre | Précision | Chiffres significatifs | |
| Simple précision | 32 bits | 1 bit | 8 bits | 23 bits | 24 bits | environ 7 | |
| Double précision | 64 bits | 1 bit | 11 bits | 52 bits | 53 bits | environ 16 |
Voici comment les choses se font sous Linux/Windows (en format simple précision) : on remarquera l'absence de multiplication et de calcul flottant :
// Serge Moutou avril 2013 version 0.9
// ************ Mai 2014 version 1.0 : remplacement pointeur par union
//** Ne peut pas fonctionner avec avr-gcc pour lequel les tailles
//** float (32 bits) et int (16 bits) ne correspondent pas !
//** Sous Linux/Windows les tailles sont toutes les deux 32 bits
float HexQ3_13ToFloat2(int val){
union {
float temp;
int f_temp;
} u;
int i_temp;
unsigned char exposant=129;//,*p;
signed char i;
if (val < 0) i_temp = -val; else i_temp = val;
for (i=15;i>=0;i--) {
if (i_temp & (1<<i)) {
// on efface le '1' trouvé :
i_temp= i_temp & ~(1<<i);
break;// on sort de la boucle
}
exposant--;
}
u.f_temp = exposant;
u.f_temp <<=23;
u.f_temp = u.f_temp|(i_temp << (23-i));
if (val < 0) return -(u.temp); else return u.temp;
}
2°) On va réaliser la conversion ci-dessus dans le matériel (en VHDL donc). En clair, notre cœur CORDIC va continuer à travailler en virgule fixe, mais le résultat sera converti en flottant par le matériel puis retourné au processeur.
Pour éviter de multiplier les PORTs de l'AVR, on va utiliser un FIFO dans lequel on viendra ranger les 8 octets correspondants aux deux nombres flottant du résultat.
Trouver une machine d'états qui fait le calcul de conversion de la question 1 et remplit un FIFO avec les 8 octets des deux résultats de CORDIC.
Conversion du résultat en chaîne de caractères de manière matérielle
[modifier | modifier le wikicode]Nous nous proposons maintenant de réaliser une conversion en chaîne de caractères des résultats en vue d'un affichage dans l'hyperterminal comme dans l'exercice qui utilisait "HexQ3_13ToString". Notre résultat devra avoir le format :
signe digit1 '.' digit2 digit3 digit4
c'est-à-dire 6 caractères (7 en ajoutant le zéro de fin de chaîne) et ceci pour le sinus et le cosinus. Pour éviter d’avoir un nombre de PORTs trop important, vous allez utiliser un FIFO comme dans l'exercice précédent.
Remplacer CORDIC par des valeurs pré-calculées en mémoire
[modifier | modifier le wikicode]Avant toute discussion, rappelons que le calcul CORDIC nécessite des valeurs pré-calculées donc de la mémoire. Calculons la taille mémoire que l’on a utilisé dans notre implantation.
Les mémoires peuvent mémoriser des valeurs prédéterminées.
Mémoire pour notre cœur CORDIC
[modifier | modifier le wikicode]Le cœur CORDIC déjà présenté nécessitait de la mémoire : il devait mémoriser les valeurs de . Mais cela représente une très petite taille car i varie de 0 à 13 (ce n’est pas la peine d'aller au-delà pour le format Q3.13). Cela fait donc 14 valeurs en format Q3.13 soit 14x16 bits = 28 octets. Trouver cela dans un FPGA ne pose aucune difficulté !
Bien sûr si l’on augmente la précision il faudra plus de mémoire mais la croissance est linéaire en i.
Mémoire pour éviter les calculs
[modifier | modifier le wikicode]Si l’on désire concurrencer CORDIC par une mémoire vous avez deux solutions :
- on mémorise toutes les possibilités sur les angles en format Q3.13
- on mémorise quelques valeurs et si l’on tombe en dehors on fait une interpolation linéaire.
Calculons la taille de la mémoire pour le premier cas qui est le plus défavorable. Il est facile de voir que l'angle varie entre les valeurs hexadécimales . Cela fait 12868 cases mémoires pour la partie positive si l’on s'en tient à mémoriser cette seule partie. Chacune des cases étant de deux octets on voit qu’il faut 25 736 octets soit environ 32 ko.
Généralisation de CORDIC
[modifier | modifier le wikicode]En introduisant un facteur μ, on peut généraliser au cas linéaire et aux fonctions hyperboliques:
Résumé pour CORDIC universel
[modifier | modifier le wikicode]Exercice
[modifier | modifier le wikicode]Pour comprendre les dessins ci-dessus et négliger les détails de l'implémentation (matérielle ou logicielle), on vous demande de prendre le mode circulaire, d'initialiser x à 1/K et y à 0 (les entrées sont à gauche) et de dire ce qui sortira du coprocesseur CORDIC.
Étude d'un cœur CORDIC généralisé
[modifier | modifier le wikicode]Nous avons trouvé chez Opengores.org cœur CORDIC de Richard Herveille fonctionnant en mode rotation et en mode vectorisé. Nous allons l'étudier brièvement maintenant.
Un coprocesseur qui réalise un programme
[modifier | modifier le wikicode]Dans cette section nous allons nous intéresser au cœur CORDIC généralisé de la section précédente et le transformer en une entité possédant suffisamment d'instructions pour pouvoir réaliser l'un des calculs CORDIC généralisé. D'une certaine manière notre coprocesseur deviendra donc un processeur avec une UAL un peu spéciale, un compteur programme, une mémoire programme et données.
Généralité sur l'interfaçage d'un coprocesseur
[modifier | modifier le wikicode]Interfaçage avec des PORTs
[modifier | modifier le wikicode]Interfaçage avec des mémoires
[modifier | modifier le wikicode]Voir aussi
[modifier | modifier le wikicode]Liens internes
[modifier | modifier le wikicode]- CORDIC qui est l’article de référence dans wikipédia
- (en) CORDIC wikibook en anglais beaucoup plus technique que le précédent article
- (en) CORDIC wikiversity
- CORDIC sur Arduino dans le livre sur les AVRs
- CORDIC et MSP430 dans le chapitre 18 de ce livre
Challenges
[modifier | modifier le wikicode]- ECE 4530 Codesign Challenge:Assignments and Results Le dernier Challenge est sur CORDIC
Articles
[modifier | modifier le wikicode]- (en) Speeding up the CORDIC algorithm with a DSP
- cours en anglais sur la représentation des nombres flottants
- Slides en anglais sur les nombres flottants
- DESIGN OF SINGLE PRECISION FLOAT ADDER (32-BIT NUMBERS) ACCORDING TO IEEE 754 STANDARD USING VHDL
Code C pour démarrer l'arithmétique virgule flottante
[modifier | modifier le wikicode]| Le premier lien (Mike Field) ci-dessous n'est plus disponible et c'est bien dommage ! |
Custom flotaing point (Mike Field) nous a servi de point de départ dans un autre chapitre. Nous y présentons un code fonctionnel pour l'addition en nombre flottant en C (sans la librairie standard de calcul flottant).
Livres
[modifier | modifier le wikicode]- Patrick R. Schaumont "A Practical Introduction to Hardware Software Codesign" Springer (2010). Le chapitre 12 est consacré à CORDIC
- Reconfigurable Computing: The Theory and Practice of FPGA-Based Computation édité par Hauck, Scott et DeHon, Andre (2010). Le chapitre 25 aborde les architectures CORDIC

























































![{\displaystyle C_{i}={\begin{pmatrix}1&-\sigma _{i}\delta _{i}\\[3pt]\sigma _{i}\delta _{i}&1\\\end{pmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dff1e17ee3ec4f8c44e878bdf89bdb67e203b0f1)
![{\displaystyle R(\alpha )={\begin{pmatrix}\cos \alpha &-\sin \alpha \\[3pt]\sin \alpha &\cos \alpha \\\end{pmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6caf3887e29dff35f5ef15dd5dd8a143f7beba1)
![{\displaystyle R(\alpha _{i})={\begin{pmatrix}\cos \alpha _{i}&-\sigma _{i}\sin \alpha _{i}\\[3pt]\sigma _{i}\sin \alpha _{i}&\cos \alpha _{i}\\\end{pmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6ea84ae4cbce7631149893f860ae53b047d7ab21)




![{\displaystyle C_{i}={\begin{pmatrix}1&-\sigma _{i}\delta _{i}\\[3pt]\sigma _{i}\delta _{i}&1\\\end{pmatrix}}={1 \over cos(\alpha _{i})}\cdot {\begin{pmatrix}\cos \alpha _{i}&-\sigma _{i}\sin \alpha _{i}\\[3pt]\sigma _{i}\sin \alpha _{i}&\cos \alpha _{i}\\\end{pmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f282189cdbf6137c727093ab44b0db0862e4df0)









































