Utilisateur:Xzapro4/Optique ondulatoire

Interférences de deux ondes obtenues par division du front d'onde

$\tau _{1}\approx \tau _{2}$

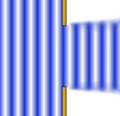
S émet une onde sphérique d'amplitude ${\mathcal {A}}={\mathcal {A}}_{0}e^{j\omega t}$

Par un dispositif approprié, on récupère deux ondes ${\mathcal {A}}_{1}(S)={\mathcal {A}}_{0}e^{j\omega t}$ ${\mathcal {A}}_{2}(S)={\mathcal {A}}_{0}e^{j\omega t}$

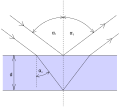
On veut déterminer ${\mathcal {A}}(M)$

${\mathcal {A}}_{1}(M,t)={\mathcal {A}}_{0}(S,t-\tau _{1})={\mathcal {A}}_{0}e^{j\omega (t-\tau _{1})}$
${\mathcal {A}}_{2}(M,t)={\mathcal {A}}_{0}(S,t-\tau _{2})={\mathcal {A}}_{0}e^{j\omega (t-\tau _{2})}$
$\tau _{1}={\frac {(SM)_{1}}{c}}$
$\tau _{2}={\frac {(SM)_{2}}{c}}$

${\mathcal {A}}(M,t)={\mathcal {A}}_{0}e^{j\omega t}\left(e^{-j\omega {\frac {(SM)_{1}}{c}}}+e^{-j\omega {\frac {(SM)_{2}}{c}}}\right)$

$\delta =(SM)_{2}-(SM)_{1}$ est la différence de chemin optique, ou différence de marche

$I(M)=\langle {\mathcal {A}}(M,t)\cdot {\mathcal {A}}(M,t)^{*}\rangle$

${\begin{aligned}I(M)&=\langle {\mathcal {A}}(M,t)\cdot {\mathcal {A}}(M,t)^{*}\rangle \\&={\mathcal {A}}_{0}^{2}\langle \left(e^{-j\omega {\frac {(SM)_{1}}{c}}}+e^{-j\omega {\frac {(SM)_{2}}{c}}}\right)\left(e^{-j\omega {\frac {(SM)_{1}}{c}}}+e^{-j\omega {\frac {(SM)_{2}}{c}}}\right)^{*}\rangle \\&={\mathcal {A}}_{0}^{2}\langle \left(e^{-j\omega {\frac {(SM)_{1}}{c}}}+e^{-j\omega {\frac {(SM)_{2}}{c}}}\right)\left(e^{j\omega {\frac {(SM)_{1}}{c}}}+e^{j\omega {\frac {(SM)_{2}}{c}}}\right)\rangle \\&={\mathcal {A}}_{0}^{2}\langle 2+2\cos \left({\frac {\omega }{c}}(SM)_{2}-(SM)_{1}\right)\rangle \\&=2{\mathcal {A}}_{0}^{2}\langle 1+\cos \left({\frac {\omega \delta }{c}}\right)\rangle \\&=2{\mathcal {A}}_{0}^{2}\langle 1+\cos \left(2\pi \delta {\frac {nu}{c}}\right)\rangle \\&=2{\mathcal {A}}_{0}^{2}\langle 1+\cos \left(2\pi \delta {\frac {1}{\lambda _{0}}}\right)\rangle \\&=4{\mathcal {A}}_{0}^{2}\cos \left({\frac {\pi \delta }{\lambda _{0}}}\right)^{2}\\\end{aligned}}$

$I_{0}={\mathcal {A}}_{0}^{2}$

$\sigma _{0}={\frac {1}{\lambda _{0}}}$ nombre d'onde

$I(M)=4I_{0}\cos(\pi \sigma _{0}\delta )^{2}$

Sans interférences, on aurait $I(M)=2I_{0}$ . Avec interférences, on obtient un terme modulant.

On appelle frange d'interférence l’ensemble des points M de l'écran tels que $\delta (M)$ est constant.

Trous d'Young

$S_{2}M-S_{1}M={\rm {cste}}$

Les lignes de niveau de δ sont des hyperboloïdes de révolution autour de $(S_{1}S_{2})$

Anneaux de Newton

Franges brillantes $\rho _{B}={\sqrt {R\lambda _{0}\left(l-{\frac {1}{2}}\right)}}$

Franges sombres $\rho _{S}={\sqrt {R\lambda _{0}l}}$

Lumière polychromatique

$I=4I_{0}\left(1+\cos \left(\pi \delta \left({\frac {1}{\lambda _{1}}}+{\frac {1}{\lambda _{2}}}\right)\right)\cos \left(\pi \delta \left({\frac {1}{\lambda _{1}}}-{\frac {1}{\lambda _{2}}}\right)\right)\right)\approx 4I_{0}\left(1+\cos \left({\frac {2\pi \delta }{\lambda }}\right)\cos \left(\pi \delta {\frac {\Delta \lambda }{\lambda ^{2}}}\right)\right)$

Diffraction trou rectangulaire

${\begin{aligned}{\mathcal {A}}(M)&=\iint _{S}k{\mathcal {A}}_{0}e^{j2\pi n\sigma _{0}{\frac {xX+yY}{f'}}}{\rm {d}}^{2}S\\&=\int _{x=-a}^{x=a}\int _{y=-b}^{y=b}k{\mathcal {A}}_{0}e^{j2\pi n\sigma _{0}{\frac {xX}{f'}}}e^{j2\pi n\sigma _{0}{\frac {yY}{f'}}}{\rm {d}}x{\rm {d}}y\\&=k{\mathcal {A}}_{0}\left(\int _{x=-a}^{x=a}e^{j2\pi n\sigma _{0}{\frac {xX}{f'}}}{\rm {d}}x\right)\left(\int _{y=-b}^{y=b}e^{j2\pi n\sigma _{0}{\frac {yY}{f'}}}{\rm {d}}y\right)\\&=k{\mathcal {A}}_{0}\left({\frac {e^{j2\pi n\sigma _{0}{\frac {aX}{f'}}}-e^{-j2\pi n\sigma _{0}{\frac {aX}{f'}}}}{2j\pi n\sigma _{0}{\frac {X}{f'}}}}\right)\left({\frac {e^{j2\pi n\sigma _{0}{\frac {bY}{f'}}}-e^{-j2\pi n\sigma _{0}{\frac {bY}{f'}}}}{2j\pi n\sigma _{0}{\frac {Y}{f'}}}}\right)\\&=k{\mathcal {A}}_{0}{\frac {\sin \left(2\pi n\sigma _{0}{\frac {aX}{f'}}\right)}{\pi n\sigma _{0}{\frac {X}{f'}}}}{\frac {\sin \left(2\pi n\sigma _{0}{\frac {bY}{f'}}\right)}{\pi n\sigma _{0}{\frac {X}{f'}}}}\\&=4abk{\mathcal {A}}_{0}{\frac {\sin \left(2\pi n\sigma _{0}{\frac {aX}{f'}}\right)}{2a\pi n\sigma _{0}{\frac {X}{f'}}}}{\frac {\sin \left(2\pi n\sigma _{0}{\frac {bY}{f'}}\right)}{2b\pi n\sigma _{0}{\frac {X}{f'}}}}\\&=4abk{\mathcal {A}}_{0}\,{\rm {sinc}}\left(2\pi n\sigma _{0}{\frac {aX}{f'}}\right){\rm {sinc}}\left(2\pi n\sigma _{0}{\frac {bY}{f'}}\right)\\\end{aligned}}$

$I(M)=(4abk{\mathcal {A}}_{0})^{2}{\rm {sinc}}\left(2\pi n\sigma _{0}{\frac {aX}{f'}}\right)^{2}{\rm {sinc}}\left(2\pi n\sigma _{0}{\frac {bY}{f'}}\right)^{2}$

$I_{0}=(4abk{\mathcal {A}}_{0})^{2}$

Maximum absolu en (X,Y)=(0,0)

Minimums nuls : $X={\frac {kf'}{2na\sigma _{0}}}$ et $Y={\frac {lf'}{2na\sigma _{0}}}$ , $(k,l)\in (\mathbb {Z} ^{*})^{2}$

Trou circulaire

Tache d'airy : $\rho =0,61{\frac {\lambda _{0}f'}{a}}$

Fente

${\mathcal {A}}(M)=k{\mathcal {A}}_{0}2b2a{\rm {sinc}}(2\pi a\sigma _{0}\sin(\theta ))$

$u=2\pi a\sigma _{0}\sin(\theta )$ , $I_{0}=4abk{\mathcal {A}}_{0}$

$I(M)=I_{0}{\rm {sinc}}(u)^{2}$

Deux fentes

$I(M)=4(4abk{\mathcal {A}}_{0})^{2}{\rm {sinc}}(2\pi \sigma _{0}au)^{2}\cos(\pi \sigma _{0}hu)$

${\mathcal {D}}$ : max en u=0, nul pour $u={\frac {l\lambda _{0}}{2a}},l\in \mathbb {Z}$

${\mathcal {I}}$ : max en $u={\frac {m\lambda _{0}}{h}},m\in \mathbb {Z}$ , nul pour $u={\frac {\left(m+{\frac {1}{2}}\right)\lambda _{0}}{2a}},l\in \mathbb {Z}$

Réseau

$I(M)=N^{2}I_{0}{\rm {sinc}}(\pi \sigma _{0}au)^{2}{\frac {\sin(\pi \sigma _{0}Nhu)^{2}}{N^{2}\sin(\pi \sigma _{0}hu)^{2}}}$

Pouvoir de résolution ${\mathcal {R}}={\frac {\lambda }{\Delta \lambda }}$

Finesse $F={\frac {1}{2l}}$

Diffraction

Principe d'Huygens Fresnel

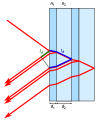
La source située en P_S génère l'onde $\psi ={\frac {A}{r_{s}}}e^{j(\omega t-kr_{s})}$

La surface S entoure P_S (peuplée de monopôles)

Le champ en P₀ est la somme des contributions des monopôles

Hypothèses Le champ en P₀ est proportionnel à

la valeur du champ incident reçu en dS à t' ${\frac {A}{r_{s}}}e^{j(\omega t'-kr_{s})}$
la surface dS
facteur de propagation sphérique ${\frac {1}{r_{0}}}e^{j(\omega (t-t')-kr_{0})}$
fonction d'obliquité $f(\theta _{0},\theta _{s})$

dS va créer une contribution dψ au point P₀ $d\psi =k{\frac {a}{r_{s}}}e^{j(\omega t'-kr_{s})}{\frac {1}{r_{0}}}e^{j(\omega (t-t')-kr_{0})}dSf(\theta _{0},\theta _{s})$ Différents problèmes :

$k\in \mathbb {R}$ : faux
$f(\theta _{0},\theta _{s})=?$

Théorème de Green $\oint _{S}\left(\psi _{1}{\vec {\nabla }}\psi _{2}-\psi _{2}{\vec {\nabla }}\psi _{1}\right){\vec {n}}dS=\int _{V}\left(\psi _{1}\Delta \psi _{2}-\psi _{2}\delta \psi _{1}\right)dV$

On essaie de réduire l'intégrale de volume à la contribution d'un point P₀

Calcul du champ en P₀ connaissant ψ et ${\frac {\partial \psi }{\partial n}}$ sur S

On choisit $\psi _{1}=\psi (x,y,z,t)$ l'onde recherchée et $\psi _{2}={\frac {1}{r_{0}}}e^{j(\omega t-kr_{0})}$ onde sphérique qui aurait P₀ comme source Pas le droit aux discontinuités : on introduit une sphère de rayon ε autour de P₀ de surface S'

Green sur SUS' $\int _{V}\psi (-k^{2}\psi _{2})\psi _{2}(-k^{2}\psi )dV=0$ $\oint _{s\cup S'}=0$

dS=\epsilon ^{2}d\Omega

$\oint _{S'}\left[\psi {\vec {\nabla }}\left({\frac {1}{r_{0}}}e^{j(\omega t-kr_{0})}\right)-{\frac {1}{r_{0}}}e^{j(\omega t-kr_{0})}{\vec {\nabla }}\psi \right]{\vec {n}}dS=\int _{\Omega }\left[\psi \left(-{\frac {1}{\epsilon ^{2}}}-{\frac {jk}{\epsilon }}\right)e^{j(\omega t-k\epsilon )}{\vec {u}}_{r}-{\frac {1}{\epsilon }}e^{j(\omega t-k\epsilon )}{\vec {\nabla }}\psi \right]{\vec {n}}\epsilon ^{2}d\Omega$

${\vec {n}}=-{\vec {u}}_{r}$

${\vec {\nabla }}\psi ={\frac {\partial \psi }{\partial r}}{\vec {u}}_{r}+{\frac {1}{r}}{\frac {\partial \psi }{\partial \theta }}{\vec {u}}_{\theta }+{\frac {1}{r\sin \theta }}{\frac {\partial \psi }{\partial \phi }}{\vec {u}}_{\phi }$

$=\int _{\Omega }\left[\psi \left({\frac {1}{\epsilon ^{2}}}{\frac {jk}{\epsilon }}\right)e^{j(\omega t-k\epsilon )}+{\frac {1}{\epsilon }}e^{j(\omega t-k\epsilon )}{\vec {\nabla }}\psi \right]\epsilon ^{2}d\Omega$

$\epsilon \to 0$

$=\int _{V}\psi e^{j\omega t}d\Omega =\psi (P_{0})e^{j\omega t}4\pi$

Intégrale d'Helmoltz Kirchhoff

$\psi (P_{0})=-{\frac {1}{4\pi }}\oint _{S}\left[\psi {\vec {\nabla }}\left({\frac {1}{r_{0}}}e^{j(\omega t-kr_{0})}\right)-{\frac {1}{r_{0}}}e^{j(\omega t-kr_{0})}{\vec {\nabla }}\psi \right]{\vec {n}}dS$

Médias

Category:Polarization