Aller au contenu

Utilisateur:Shouissa98/Modélisation des Réseaux (M1 SIREN, 2022)/Activité B

Une page de Wikiversité, la communauté pédagogique libre.

Réseau

[modifier | modifier le wikicode]
  1. Cas concret de mon réseau : Skander -> couscous, chakchouka, pâte bolognaise, la house, la Zumba, footbal, tennis, guitare, batterie
  2. Deux camarades avec des noeuds similaires: Sarah-> les sushis, la bière belge, HipHop, la Zumba, le Charleston, équitation, tennis, Piano Oscar --> poulet, bavette, fernet, claquettes, piano, batterie, rugby, pelote basque, surf
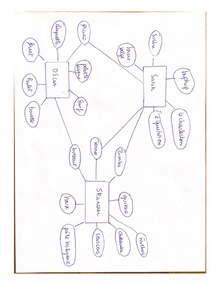
  3. Vous trouverez à droite mon réseau unique avec les noeuds et liens de ces trois réseaux. 3

Questions

[modifier | modifier le wikicode]
  1. En ignorant l'orientation des liens, la photo ci-dessus est un graphe connexe avec une composante connexe. Il existe un chemin entre chaque paire de sommets.
  2. 1. Ce réseau contient un triangle : Skander->Batterie->Oscar->Piano->Sarah->Tennis,Zumba->Skander 3. Si on prenait en compte l'orientation, il n'y aurait pas de cycles puisque ce graphe est composé d'une multitude de graphes (sommets) fortement connexe sans cycle. Il n'y a donc pas de plus petit cycle. Il n'y a aucun degré entrant pour les personnes donc pas de cycle.
  3. 1.
Noeud Cible des liens
[Skander] couscous, chakchouka, pâte bolognaise, la house, la Zumba, footbal, tennis, guitare, batterie
[Sarah] les sushis, la bière belge, HipHop, la Zumba, le Charleston, équitation, tennis, Piano
[Oscar] poulet, bavette, fernet, claquettes, piano, batterie, rugby, pelote basque, surf

Le degré entrant des personnes est zéro, ainsi que le degré sortant de n'importe que élément. On note dans la liste et par le graphe dessiné que la plupart des éléments ont un degré entrant de 1, car apparaît une seule fois dans la liste d'une seule personne, tandis que quatre éléments ont un degré égal a 2, car partagé par deux personnes également une fois dans la liste de chacune. Un élément figure dans les trois listes. D'une telle façon qu'on peut écrire le tableau de degrés :

Noeud Entrée Sortie
Skander 0 9
Sarah 0 8
Oscar 0 9
Zumba 2 0
Tennis 2 0
Batterie 2 0
Piano 2 0

3.2. Distribution du nombre de degrés graphe non orienté sous forme de tableau:

Dans le cas d'un graphe non orienté, il suffit de reprendre le tableau ci-dessus, et d'additionner entrant et sortant puisqu'il n'y a pas de flèche allant dans les deux sens (uniquement de la personne vers ses éléments). Pour tous les éléments absents, ils ont un degré de 1.

Noeud Degré
Skander 9
Sarah 8
Oscar 9
Zumba 2
Tennis 2
Batterie 2
Piano 2

4. La matrice d'adjacence :

Noeud/Noeud Skander Sarah Oscar Zumba Tennis Batterie Piano
Skander 0 0 0 1 1 1 0
Sarah 0 0 0 1 1 0 1
Oscar 0 0 0 0 0 1 1
Zumba 1 1 0 0 0 0 0
Tennis 1 1 0 0 0 0 0
Batterie 1 0 1 0 0 0 0
Piano 0 1 1 0 0 0 0
Récupérée de « https://fr.wikiversity.org/w/index.php?title=Utilisateur:Shouissa98/Modélisation_des_Réseaux_(M1_SIREN,_2022)/Activité_B&oldid=944802 »