Utilisateur:Mathildecomte603/Modélisation des Réseaux (M1 SIREN, 2022)/Activité B
Le niveau le plus granulaire de mon réseau était tel que :
Mathilde -> Musculation, RPM, Guitare, Piano, Vin, Ramens, Salsa, Bachata.
J'ai remarqué que Alice et Nina-Lou avait des composantes similaires aux-miennes, caractérisées en gras :
Alice -> Clarinette, Guitare, Piano, Vin, Cheesecakes, Omelettes, Handball, Basketball, Valse, Danse contemporaine
Nina-Lou -> Pilates, Kite-surf, Fromage Truffe, Caipirinha, Fajitas, Volley-ball, Piano, Salsa
Voici le nouveau réseau formalisé en schéma :

Question 1
[modifier | modifier le wikicode]On a ici une unique composante connexe qui est le graphe, en effet toutes les personnes sont liées à [Mathilde] et tous les autres noeuds sont liés à au moins [Alice] et/ou [Nina-Lou].
Concernant les composantes fortement connexes, chaque noeud en est une car en prenant en compte l'orientation du graphe il n'existe pas de noeuds entre lesquels on puisse aller et revenir.
Les composantes fortement connexes sont donc : Mathilde, Alice, Nina-Lou, Musculation, RPM, Guitare, Piano, Vin, Ramens, Salsa, Bachata, Pilates, Site-Surf, Fromage Truffe, Caipirinha, Fajitas, Volley-ball, Cheesecakes, Omelettes, Handball, Basketball, Valse, Danse contemporaine, Clarinette.
Question 2
[modifier | modifier le wikicode]- Il n'y a pas de triangle dans ce réseau. On ne peut partir que d'un élément A vers un autre élément B, c'est tout.
- Les plus petits cycles existants sont à 4 pas, comme par ex :
Mathilde - Guitare - Alice - Piano - Mathilde
Mathilde - Salsa - Nina-Lou - Piano - Mathilde
3. Si on prenait en compte l'orientation du graphe il n'y aurait pas de cycle dans ce réseau (les composantes Mathilde, Alice et Nina-Lou ne possèdent que des liens sortant).
Question 3
[modifier | modifier le wikicode]| Noeuds | Degré non-orienté | Degré sortant | Degré entrant |
|---|---|---|---|
| Mathilde | 8 | 8 | 0 |
| Alice | 10 | 10 | 0 |
| Nina-Lou | 8 | 8 | 0 |
| Piano | 3 | 0 | 3 |
| Guitare | 2 | 0 | 2 |
| Vin | 2 | 0 | 2 |
| Salsa | 2 | 0 | 2 |
| 17 autres noeuds | 1 | 0 | 1 |
Distribution des degrés :
| Degrés | #Non-orientés | #Sortant | #Entrant |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 17 | 0 | 17 |
| 2 | 3 | 0 | 3 |
| 3 | 1 | 0 | 1 |
| 8 | 2 | 2 | 0 |
| 10 | 1 | 1 | 0 |
Question 4
[modifier | modifier le wikicode]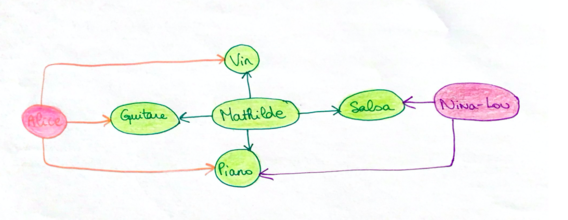
Voici mon réseau simplifié :
Matrice d'adjacence :
| Mathilde | Alice | Nina-Lou | Guitare | Piano | Vin | Salsa | |
|---|---|---|---|---|---|---|---|
| Mathilde | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| Alice | 0 | 0 | 0 | 1 | 1 | 1 | 0 |
| Nina-Lou | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| Guitare | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Piano | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Vin | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Salsa | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Projections non-orientées sur les personnes :
| Mathilde | Alice | Nina-Lou | Guitare | Piano | Vin | Salsa | |
|---|---|---|---|---|---|---|---|
| Mathilde | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| Alice | 0 | 0 | 0 | 1 | 1 | 1 | 0 |
| Nina-Lou | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| Guitare | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| Piano | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| Vin | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| Salsa | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
- Il n'y a qu'une seule composante connexe et la plus grande distance est 3 et on la trouve pour aller de [ Vin ] à [ Nina-Lou ] ou de [ Salsa ] à [ Alice ].
Pour ce qui est du graphe qui établit la synthèse de ce réseau simplifié, le diamètre est de 5. En effet, on peut utiliser le chemin suivant :
Δ {Mathilde, vin, Alice, salsa, Nina-Lou, piano} = 5.
3. Pour transformer ce réseau simplifié en un réseau fortement connexe, il faudrait que les noeuds communs entre deux personnes le soient avec les trois. Il faudrait que les centres d'intérêts évoqués dans le réseau soient partagés par les 3 individus Mathilde, Alice et Nina-Lou. Ainsi, il faudrait rajouter les 3 liens en marrons qui relient donc :
Alice - Salsa
Nina-Lou - Guitare
Nina-Lou - Vin
Ainsi, Alice devrait commencer la Salsa, et Nina-Lou devrait commencer la guitare et aimer le vin.

