Utilisateur:Asma Zaafrane/Modélisation des Réseaux (M1 SIREN, 2022)/Activité B
Réseau:
[modifier | modifier le wikicode]1- Mon réseau:
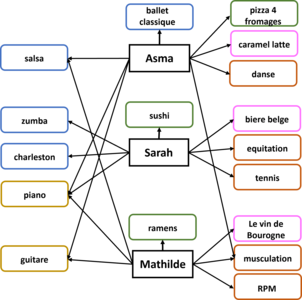
Asma -> (pizza 4 fromages, caramel latte, ballet classique, salsa, piano, guitare, danse, musculation)2- Deux collègues dont les réseaux de l'activité A ont des nœuds en commun avec le miens: Sarah et Mathilde jouent du piano comme moi et Mathilde joue de la guitare aussi et fait de la musculation et danse de la salsa.
Sarah-> (sushis, biere belge, Hip Hop, Zumba, Charleston, piano, equitation, tennis)
Mathilde -> (ramens, le vin de Bourgogne, la bachata, salsa, piano, guitare, musculation, RPM)3- Un réseau unique :
Asma -> (pizza 4 fromages, caramel latte, ballet classique, salsa, piano, guitare, danse, musculation)
Sarah-> (sushis, biere belge, Hip Hop, Zumba, Charleston, piano, equitation, tennis)
Mathilde -> (ramens, le vin de Bourgogne, la bachata, salsa, piano, guitare, musculation, RPM)
pizza 4 fromage -> (cas de pizza)
pizza -> (type de plat)
caramel latte -> (cas de café)
café -> (type de boisson)
ballet classique -> (cas de ballet)
ballet -> (cas de danse)
sushis -> (type de plat)
biere belge -> (cas de biere)
biere -> (type de boisson)
Hip Hop -> (cas de danse)
Zumba -> (cas de danse)
Charleston -> (cas de danse)
piano -> (type d'instrument de musique)
equitation -> (cas de sport)
tennis -> (cas de sport)
danse -> (type de Activité physique)
sport -> (type de Activité physique)
ramens -> (type de plat)
le vin de Bourgogne -> (cas de vin)
vin -> (type de boisson)
Hip Hop -> (cas de danse)
la bachata -> (cas de danse)
salsa -> (cas de danse)
guitare -> (type d'instrument de musique)
musculation -> (cas de sport)
RPM -> (cas de sport)
Questions
[modifier | modifier le wikicode]1. Une seule composante est connexe, c'est tout le graphe, car par construction toutes les personnes sont liées à [ Asma ], et tous les autres nœuds sont liés à au moins une personne.
Tous les nœuds du graph sont fortement connexes puisqu'elles prennent en compte l'orientation des liens.
2.
En ignorant l'orientation des liens :
- Si on ne prend pas en compte l'orientation des liens, ce réseau ne contient pas de triangles. Le graphe est biparti les personnes ne se connectent pas entre elles, et les nœuds objet ne se connectent pas entre eux. Un triangle exigerait donc une séquence du type
[ personne A ] – [ objet X ] – [ personne B ] – [ personne A ], ou l'équivalant en partant d'un objet, ce qui n'est pas possible. - Le plus petit cycle que mon réseau contient est de taille 4 (A-B-C-D-A). Par exemple: [ Sarah ] - [ piano ] - [ Mathilde ] - [ piano ] - [ Sarah ]
En prenant en compte l'orientation des liens :
- Si on prenait en compte l'orientation des liens, il n'y aura ni triangles ni cycles
3. Graphique de distribution de degrés:
Les degrés du graphe:
| Nœud(s) | Degré non-orienté | Degré sortant | Degré entrant |
| Asma | 8 | 8 | 0 |
| Sarah | 7 | 7 | 0 |
| Mathilde | 7 | 7 | 0 |
| Piano | 3 | 0 | 3 |
| Guitare | 2 | 0 | 2 |
| Salsa | 2 | 0 | 2 |
| Musculation | 2 | 0 | 2 |
| 13 autres nœuds | 1 | 0 | 1 |
Non-orienté:
| Degrès | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Nombre | 0 | 13 | 3 | 1 | 0 | 0 | 0 | 2 | 1 |
Graphique:

Graphique de distribution de degrés sortant et entrant du graphe orienté
Degrés entrants:
| Degrés entrants | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| # | 3 | 13 | 3 | 1 | 0 | 0 | 0 | 0 | 0 |

Degrés sortants:
| Degrés sortants | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| # | 17 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 1 |

4. La matrice d'adjacence
Mon réseau simplifié:

Matrice adjacente:
| Asma | Sarah | Mathilde | Piano | Guitare | Salsa | Musculation | |
| Asma | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| Sarah | 0 | 0 | 0 | 1 | 0 | 1 | 0 |
| Mathilde | 0 | 0 | 0 | 1 | 1 | 0 | 1 |
| Piano | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Guitare | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Salsa | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Musculation | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Projection non-orientée:
- Sur les personnes:
[ Asma ] - piano - [Mathilde]
[ Asma ] - piano - [Sarah]
[Asma ] - guitare - [ Mathilde]
[ Asma ] - Salsa - [Sarah]
[ Asma ] - musculation - [Mathilde]
- sur les objets:
[ piano ] - Asma - [ guitare ]
[ piano ] - Asma - [ salsa ]
[ piano ] - Asma - [ musculation ]
[ guitare ] - Asma - [ musculation ]
[ guitare ] - Asma - [ salsa ]
[ guitare ] - Mathilde - [ piano ]
[ guitare ] - Mathilde - [ musculation ]
[ salsa ] - Sarah - [ piano ]
- Diamètre non-orienté : Il n'y a qu'une seule composante connexe et la plus grande distance est 4 et on la trouve pour aller de [musculation] à [Sarah]
3. Réseau fortement connexe :
Dans un réseau fortement connexe on peut partir et arriver entre n'importe quels deux nœuds. Cela implique que chaque nœud doit avoir au moins un lien entrant et un lien sortant.
Dans mon réseau, les personnes n'ont pas de lien entrant, il faudrait donc ajouter au moins 3 liens pour qu'on puise arriver à chacune des 3 personnes. A son tour, les objets aussi n'ont pas de lien sortant, même problématique. Voyons donc si on peut ajouter 3 liens partant des objets vers les personnes, d'une telle sorte qu'on puisse circuler dans le graphe. Si on rajoute au graphe les liens :
[guitare] -> [Asma]
[musculation] -> [Mathilde]
[salsa] -> [Sarah]

