Utilisateur:Alina Viatkina/Modélisation des Réseaux (M1 SIREN, 2022)/Activité B

Réseau

Mon réseau : Alina -> le bortch, les pirojki, le bœuf bourguignon, la valse, la polka, le football, le patinage, la guitare, la flute.
J’ai trouvé les réseaux de Alice et Scander qui ont des nœuds en commun avec le mien :

Alice -> omelettes, cheesecakes; vin blanc, danse contemporaine, valse, clarinette, guitare, piano, basketball, handball
Skander -> couscous, chakchouka, pâte bolognaise, la house, la Zumba, football, tennis, guitare, batterie

3. Voici ci-contre le réseau composé des cas concrets de nos trois réseaux :

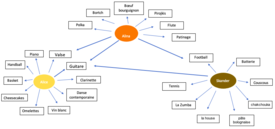
Questions

Question 1

En ignorant l'orientation des liens, l'image ci-dessus est un graphe connexe avec une composante connexe. Il existe un chemin entre chaque paire de sommets. Si on se place dans le cas d'un graphe orienté. Les composantes fortement connexes sont : Alina, Alice, Skander, le bortch, les pirojki, le bœuf bourguignon, la valse, la polka, le football, le patinage, la guitare, la flute, omelettes, cheesecakes; vin blanc, danse contemporaine, clarinette, piano, basketball, handball, couscous, chakchouka, pâte bolognaise, la house, la Zumba, tennis, batterie.

Question 2

2. 1. Il n'y a pas de triangle

2. 2. Le plus petit cycle de ce réseau, en ne considérant pas l'orientation, possède une distance de 4 : (Alina - Valse - Alice - Guitare - Alina) ou (Alina - Football - Skander - Guitare - Alina).

2. 3. Si on prenait l'orientation des liens, il n'y aurait pas de cycles dans ce réseau. En effet, les personnes n'ont que des liens sortants et non entrants.

Question 3

3. Distribution des degrés du graphe non-orientés :

Non-orientés
Noeud	Degrés
Alice	10
Alina	9
Skander	9
Guitare	3
Valse	2
Football	2

Distribution du nombre de degrés graphe orienté sous forme de tableau :

Orienté
Noeud	Entrée	Sortie
Alice	0	10
Alina	0	9
Skander	0	9
Guitare	3	0
Valse	2	0
Football	2	0

Degrés sortant et entrant :

d(football) = 2

d(valse) = 2

d(guitare) = 3

d(Skander) = 9

d(Alina) = 9

d(Alice) = 10

Degrés sortants

0

1

2

3

4

5

6

7

8

9

10

25

0

2

1

d ⁺(Alice) = 10

d ⁺(Alina) = 9

d ⁺(Skander) = 9

Degrés entrants
0	1	2	3
3	21	2	1

d−(football) = 2

d−(valse) = 2

d−(guitare) = 3

Question 4

Voici les matrices adjacentes pour le cas du réseau orienté et non-orienté.

Matrice adjacente pour le réseau orienté
	Guitare	Valse	Football
Alice	1	1	0
Alina	1	1	1
Skander	1	0	1
Guitare	0	0	0
Valse	0	0	0
Football	0	0	0

Matrice adjacente pour le réseau non-orienté
	Alice	Alina	Skander	Guitare	Valse	Football
Alice	0	0	0	1	1	0
Alina	0	0	0	1	1	1
Skander	0	0	0	1	0	1
Guitare	1	1	1	0	0	0
Valse	1	1	0	0	0	0
Football	0	1	1	0	0	0

4.1 Vous trouverez ci-contre l'ensemble des sous-ensemble du réseau centré sur les personnes puis sur les autres noeuds - réseau simplifié

4.2 Le diamètre représente la plus grande distance possible sur chaque composante. Pour les projections isolées des noeuds "personnes" et des autres, ces composantes connexes ont toutes un diamètre de 2.

Pour ce qui est du graphe qui établit la synthèse de ce réseau simplifié, le diamètre est de 6. En effet, on peut utiliser le chemin suivant :

(Alina, football, Skander, guitare, Alice, valse, Alina) = 6.

Correction :

4.2.1. Projections non-orientés :

Sur les personnes :

[ Alina ] - Guitare - [ Alice ]
[ Alina ] - Valse - [ Alice ]
[ Alina ] - Football - [ Skander ]
[ Skander ] - Guitare - [ Alice ]

Sur les objets :

[ Valse ] - Alice - [ Guitare ]
[ Guitare ] - Alina - [ Football ]
[ Guitare ] - Skander - [ Football ]
[ Valse ] - Alina - [ Guitare ]
[ Valse ] - Alina - [ Football ]

4.2.2 Diamètre non-orienté :

Il n'y a qu'une seule composante connexe et la plus grande distance est 3 et on la trouve pour aller de [ Alice ] à [ Football ] ou de [ Skander ] à [ Valse ].

4.3. Réseau fortement connexe :

[ Valse ] - Alina

[ Guitare ] - Alina

[ Football ] - Alina

[ Football ] - Skander

[ Guitare ] - Skander