Utilisateur:Alexercices/Modélisation des Réseaux (M1 SIREN, 2022)/Activité B
Réseau
[modifier | modifier le wikicode]1) Gardez uniquement les cas concrets de votre réseau, c'est-à-dire, le niveau le plus granulaire de réponse aux questions
Alex => Piano, Pilates, Valse, Yoga, Ukulele, Vodka, Redbull, Steak/Frites, Nouilles, Claquettes.
2) Trouvez deux collègues dont les réseaux de l'activité A ont des nœuds en commun avec le votre.
J'ai identifié que les profils d'Alice Joie et Nina-Lou Fresnil ont des points communs avec le miens.
Alex => Piano, Pilates, Valse Alice => Piano, Valse, omelettes, cheesecakes, vin blanc, danse contemporaine, clarinette, guitare, Basket, handball Nina-Lou => Piano, Pilates, fromage de truffe, fajitas, caïpirinha, salsa, kite-surf, volley-ball
3) Construisez un réseau unique avec les nœuds et liens de ces trois réseaux, toujours gardant seulement les cas concrets, dont les personnes.
Questions
[modifier | modifier le wikicode]1. Composantes connexes : les personnes (Alex, Alice, Nina-Lou)
Composantes fortement connexes (dans le cadre d'un graphe orienté) : Piano, Pilates, Valse, Yoga, Ukulele, Vodka, Redbull, Steak/Frites, Nouilles, Claquettes, omelettes, cheesecakes, vin blanc, danse contemporaine, clarinette, guitare, Basket, handball, fromage de truffe, fajitas, caïpirinha, salsa, kite-surf, volley-ball.
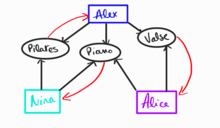
2. Voici le graphique sans prendre en compte l'orientation des liens.

1) Ce réseau ne contient pas de triangle. 2) Le plus petit cycle qu'il contient est de 4 : Nina - Piano - Alex - Pilates - Nina 3) En prenant en compte l'orientation des liens, nous n'aurions pas de cycle. En effet, il s'agit d'un réseau partant des individus vers des éléments fortement connexes et ainsi pas de degré entrant pour les individus au centre de leurs réseaux.
3. Distribution des degrés.
| Noeud | Liens |
|---|---|
| Alex | Piano, Pilates, Valse, Yoga, Ukulele, Vodka, Redbull, Steak/Frites, Nouilles, Claquettes |
| Nina-Lou | Piano, Pilates, fromage de truffe, fajitas, caïpirinha, salsa, kite-surf, volley-ball |
| Alice | Piano, Valse, omelettes, cheesecakes, vin blanc, danse contemporaine, clarinette, guitare, Basket, handball |
| Noeud | Degrés |
|---|---|
| Alex | 10 |
| Nina-Lou | 8 |
| Alice | 10 |
| Pilates, Valse | 2 |
| Piano | 3 |
| Yoga, Ukulele, Vodka, Redbull, Steak/Frites, Nouilles, Claquettes, fromage de truffe, fajitas, caïpirinha, salsa, kite-surf, volley-ball, omelettes, cheesecakes, vin blanc, danse contemporaine, clarinette, guitare, Basket, handball | 1 |
Graphe Orienté Nous nous rendons compte ici que les Noeuds (ou individus) n'ont pas de degrés entrant mais que des sortants. Ensuite, dans les liens il en existe une multitude présents une seule et unique fois dans le réseau qui auront un degré entrant de 1 (c'est le cas pour le steak/frite, le basket, le surf... non inscrit dans le tableau) . Puis, 2 liens avec 2 degrés entrants (Valse et Pilates présents au sein de 2 réseaux individuels) et finalement 1 lien (Piano) avec 3 degrés entrants ! Ce qui nous donne le tableau suivant :
| Noeuds | Entrants | Sortants |
|---|---|---|
| Alex | 0 | 10 |
| Nina-Lou | 0 | 8 |
| Alice | 0 | 10 |
| Pilates | 2 | 0 |
| Valse | 2 | 0 |
| Piano | 3 | 0 |
4. Réseau simplifié (= degré total > 1) 1)
| Noeuds/Noeuds | Alex | Nina-Lou | Alice | Pilates | Valse | Piano |
|---|---|---|---|---|---|---|
| Alex | 0 | 0 | 0 | 1 | 1 | 1 |
| Nina-Lou | 0 | 0 | 0 | 1 | 0 | 1 |
| Alice | 0 | 0 | 0 | 0 | 1 | 1 |
| Pilates | 1 | 1 | 0 | 0 | 0 | 0 |
| Valse | 1 | 0 | 1 | 0 | 0 | 0 |
| Piano | 1 | 1 | 1 | 0 | 0 | 0 |


2) Liens non orientés :
1. Projection noeuds = individus et Projection noeuds = pas des individus
2. Mes deux graphes sont connexes, il existe un chemin entre n'importe quelle paire de noeud (logique, puisque non-orienté). Les deux graphes connexes sont de la même forme et auront ainsi potentiellement le même diamètre. Pour le calculer nous pouvons faire un tableau des diamètres mais il est plus simple pour des graphes connexes de compter le nombre de liens. Ici on a diamètre = 5
3) Nous reprenons notre réseau simplifié, cette fois-ci orienté. Afin de transformer ce réseau en un réseau fortement connexe, il nous faut relier aux noeuds individus les éléments non individus. Voici ma proposition (les flèches rouges) :