Tableur EXCEL/Exercices/Exercice EXCEL Solveur
Exercices sur valeur cible
[modifier | modifier le wikicode]- Utiliser la valeur cible pour un calcul de somme
- Utiliser la valeur cible pour un calcul de log
- Utiliser la valeur cible pour un calcul de somme
- Enregistrer des nombres sur une colonne par exemple de A2 à A10
- En faire la somme en dernière ligne par exemple en A11
- Démarrer l'assistant valeur cible
- Dans Cellule à définir entrer A11 (la formule)
- Dans Valeur à atteindre la valeur que vous voulez obtenir
- Dans Cellule à modifier entrer A2 (la variable)
- Cliquer sur OK, le résultat est obtenu et la variable a été modifiée
- Utiliser la valeur cible pour un calcul de log
- Enregistrer des nombres sur une colonne par exemple de A2 à A3
- En faire le log de leur multiplication en dernière ligne par exemple en A4
- Démarrer l'assistant valeur cible
- Dans Cellule à définir entrer A4 (la formule)
- Dans Valeur à atteindre la valeur que vous voulez obtenir
- Dans Cellule à modifier entrer A2 (la variable)
- Cliquer sur OK, le résultat est obtenu et la variable a été modifiée
- Utiliser la valeur cible pour un calcul de somme
Exercice sur le solveur
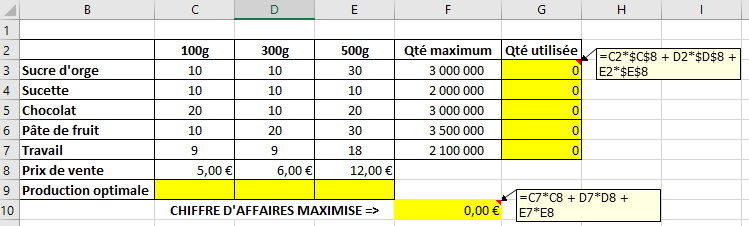
[modifier | modifier le wikicode]Une confiserie produit 4 sortes de sucrerie(sucre d'orge, sucette, chocolat, pâte de fruit) qu'elle vend sous 3 conditionnements différents (100g, 300g et 500g). Le contenu des boîtes peut être résumé dans un tableau :
La production de ces boîtes est limitée par certaines contraintes :
- on peut fabriquer au maximum 3 000 000 sucre d’orges, 2 000 000 sucettes, 3 000 000 chocolats et 3 500 000 pâtes de fruits.
- la mise en boîte des confiseries se fait en 9 minutes pour 100g, 9 minutes pour 300g et 18 minutes pour 500g.
- 15 ouvriers travaillent en moyenne 194 heures par mois.
Les boîtes sont vendues 5 € (100g), 6 € (300g) et 12 € (500g).
Soient x la quantité de 100g, y la quantité de 300g et z la quantité de 500g.
Contraintes liées à la composition des boîtes :
- Sucre d’orge : 10x + 10y + 30z <= 3 000 000
- Sucette : 10x + 10y + 10Z <= 2 000 000
- Chocolat : 20x + 10y + 20z <= 3 000 000
- Pâte de fruit : 10x + 20y + 30z <= 3 500 000
Contrainte liée au nombre de minutes de travail disponibles :
- Travail : 9x + 9y + 18z <= 2 100 000
(194*60*15*12) arrondi au nombre de minutes.
Autres contraintes : On ne produit pas des quantités négatives donc :
- x => 0
- y => 0
- z => 0
On cherche à maximiser le profit soit à maximiser : 5x + 6y + 12z
Résolution du problème à l'aide du solveur
- Représenter sous forme de tableau les contraintes exprimées plus haut.
- Lancer le solveur
- Cliquer dans la zone CELLULE CIBLE A DEFINIR et entrer la référence ou le nom de la cellule cible. Attention, celle-ci doit contenir une formule.
Pour que la valeur de la cellule cible soit aussi élevée que possible, cocher MAX Pour que la valeur de la cellule cible soit aussi petite que possible, cocher MIN Pour que la cellule de la cible contienne une valeur donnée, cocher VALEUR, puis taper la valeur dans la zone voisine.
- Cliquer dans la zone CELLULES VARIABLES et entrer le nom ou la référence de chaque cellule variable. Les cellules variables doivent être associées directement ou indirectement à la cellule cible.
- Cliquer dans la zone CONTRAINTES et entrer les contraintes que vous souhaitez appliquer en utilisant le bouton AJOUTER
- Entrer les informations suivantes dans les différentes zones :
- Cliquer sur le bouton RESOUDRE
- Cocher l'option GARDER LA SOLUTION DU SOLVEUR et valider.
- Vous devez trouver comme solution :
NB : le résultat donne un nombre réel pour les boîtes 500g, ce type d'erreur (il n'est pas possible de produire des parties de boîtes) peut être résolu en ajoutant les contraintes suivantes dans le solveur:
- $C$8=Entier
- $D$8=Entier
- $E$8=Entier
Pour atteindre le chiffre d'affaires maximal de 1 350 000 €, il faudrait produire 50 000 boites de 100g, 50 000 boîtes de 300g et 66 667 boîtes de 500g.