Statistique et économétrie/La Variable aléatoire - Définition
La notion de variable aléatoire formalise l’association d’une valeur du résultat d’une expérience aléatoire.
Exemple : on considère une expérience aléatoire consistant à lancer deux pièces de monnaie. Alors Ω {(P ; P), (P ; F), (F ; F), (F ; P)}. La probabilité de chacun est de 1/4 et ainsi, la somme de toutes les probabilités est égale à 1 => ∑▒〖Px=1〗
Une variable aléatoire va associer une valeur à chacun des éléments de Ω. Considérant la variable aléatoire représentant le nombre de faces obtenu.
Exemple : lancé de deux pièces de monnaie, quel est le nombre de face qu’on peut obtenir ?
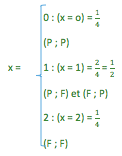
C’est une variable quantitative discrète donc la représentation graphique est en bâton.
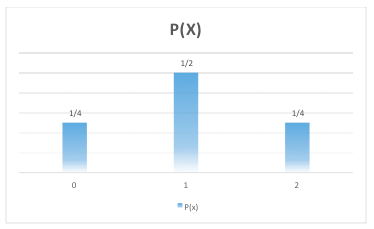
Une variable aléatoire discrète prend uniquement une valeur entière.
Une distribution de probabilité, noté Px(x), est une fraction qui associe à chaque valeur entière une probabilité. Distribution de probabilité d’une variable discrète est :
Px(x) = Pr (X = x)
Pr = probabilité
x = o => Px(x) = 1/4 = Px(0)
Px(1) = 1/2
Px(2) = 1/4
La fonction de répartition est définie par Fx(x) = ∑〖Px(x)〗 = Pr(X ≤ x)
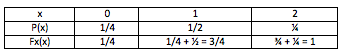
L’espérance mathématique d’une variable aléatoire discrète est définie de la manière suivante :
E(x) = ∑〖Px(x)〗.x
Soit = (0. ¼) + (1. ½) + (2. ¼)
La variance : V(x) = ∑〖Px(x) xi^2-E(x)²〗
Calcul de la Variance :

V(x) = (1/4 * 0) + (1/2 * 1) + (1/4 * 4) - 1² = 0.5


