Statistique et économétrie/Distributions à un caractère – Caractéristiques de distribution à un caractère
Le mode[modifier | modifier le wikicode]
Variable quantitative discrète[modifier | modifier le wikicode]
Le mode correspond à la valeur de la variable pour laquelle l’effectif (ou la fréquence) est le plus grand.
Exemple : Le recensement des familles dans une population régionale dont le nombre d’enfants de moins de 14 ans est le suivant :
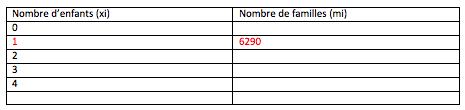
Ici, le mode correspond à la valeur 1. La majorité des familles possédant un nombre d’enfants de moins de 14 ans égale à 1.
Variable quantitative continue[modifier | modifier le wikicode]
La classe modale est la classe dont la fréquence par unité d’amplitude est la plus élevée ; cette classe correspond donc au rectangle le plus haut de l’histogramme des fréquences.
Exemple : La classe modale est égale à [6 ; 10[
Détermination du mode dans le cas d’une variable quantitative continue :
ei-1 = c’est la valeur de l’extrémité de la classe modale = 6
am = Amplitude de la classe modale = 10 – 6 = 4
d1 = différence entre l’effectif de la classe modale et de la classe précédente = 3 220 753 – 2 538 643 = 682 110
d2 = différence entre l’effectif de la classe modale et de la classe suivante = 3 220 753 – 3 174 548 = 46 205
6 + 4 * 682 110 / (682 110 + 45 205) = 9,75 le résultat est cohérent car il appartient bien à la classe [6 ; 10[
Cela signifie que la majorité des enfants sont scolarisés à 9,75 ans
La médiane[modifier | modifier le wikicode]
La médiane est la valeur de la variable qui partage la série étudiée en deux sous-ensembles d’effectifs égaux.
La moyenne arithmétique[modifier | modifier le wikicode]
La moyenne arithmétique d'une variable quantitative notée xi est égale à la somme des valeurs, x1, x2,……………….. ,XN, prises par cette variable divisée par le nombre d'observations N, soit:
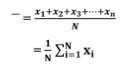
Dans le cas d'une variable continue, les observations étant groupées en classes, il convient de déterminer préalablement le centre de classe Xi et d'appliquer ensuite la formule donnée par l'équation.
Caractéristiques de dispersion
Étudier la dispersion - ou la variabilité - d'une série consiste à analyser ses fluctuations autour d'une valeur centrale.
L’Étendue[modifier | modifier le wikicode]
L'étendue est définie comme la différence entre la plus grande et la plus petite valeur de la série.
L'étendue est ainsi très simple à calculer, mais présente l'inconvénient majeur de ne dépendre que des valeurs extrêmes de la série. Ces dernières étant souvent exceptionnelles, voire aberrantes, l'étendue ne constitue qu'une mesure très imparfaite de la dispersion d'une série.
La Variance et l’écart-type[modifier | modifier le wikicode]
La variance, notée V(x), d'une variable statistique x est donnée par la moyenne arithmétique des carrés des écarts des observations xi, i = l, ..., k, à la moyenne.

L'écart-type, noté ∂x, est la racine carrée de la variance et s'exprime ainsi dans la même unité que la variable étudiée :

Plus l'écart-type est faible, plus les valeurs sont regroupées autour de la moyenne.
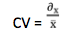
Le Coefficient de variation[modifier | modifier le wikicode]
Lorsque l'on souhaite comparer la dispersion de séries dont les unités sont différentes, par exemple la dispersion de salaires en euros et la dispersion de salaires en livres, il convient d'utiliser une mesure de dispersion relative. Le coefficient de variation, noté CV, fournit une telle mesure. Il s'agit d'un nombre sans dimension, indépendant des unités considérées, défini comme le rapport entre l'écart-type et la moyenne:
IMPORTER FORMULE



