Étude et tracé d'une fonction/Domaine de définition, limites et asymptotes

Début de la boite de navigation du chapitre

fin de la boite de navigation du chapitre

L'objet de ce premier chapitre n'est pas de définir ce que l'on entend par la notion de limite. Le lecteur est censé avoir assimilé cette notion. Si besoin, nous vous conseillons d'étudier au préalable la leçon : Limites d'une fonction. Dans ce chapitre, nous allons étudier à quoi peut nous servir la notion de limite si l'on souhaite étudier en détail une fonction. Nous allons voir que les limites nous permettent de mieux préciser le tracé de la courbe représentative d'une fonction dans un repère orthonormé.

Nous allons voir que les notions de domaine de définition, limite et asymptote sont des notions interdépendantes. C'est pour cela que nous les avons réunies dans un même chapitre.

Le domaine de définition nous indique quelles limites doivent être calculées puisque l'on calcule généralement les limites aux bornes du domaine de définition. Selon la valeur de ces limites, nous essayerons d'en déduire quel type d'asymptote doit être envisagé.

Nous allons reprendre toutes ces notions de façon détaillées ci-dessous.

Domaine de définition

Définition

Soit une fonction f à valeurs réelles. Le domaine de définition d'une fonction est le sous-ensemble des éléments de l'ensemble des nombres réels qui ont une image par f.

Pour ceux qui n'ont pas compris la définition précédente, nous pouvons aussi dire que le domaine de définition d'un fonction f est constitué de l'ensemble des nombres pour lesquels, on ne se plante pas en faisant le calcul en utilisant l'expression de f. On peut aussi dire que c'est l'ensemble des valeurs pour lesquelles notre calculatrice ne nous sort pas un message d'erreur.

Exemple 1 Soit la fonction f défini par : $f(x)={\frac {1}{1-{\frac {1}{x}}}}$ Rentrez cette fonction dans votre calculatrice et essayez de calculer f(0), f(1), f(2). qu'obtient-on ? Essayez de comprendre ce qu'il s'est passé en refaisant les calculs à la main. Corrigé Nous obtenons : ${\begin{cases}f(0)=\textstyle {message\,d'erreur}\\f(1)=\textstyle {message\,d'erreur}\\f(2)=2\end{cases}}$ Le problème vient du fait que la division par 0 n'est pas définie. Par conséquent les dénominateurs des fractions ne doivent pas être nuls. Or, si l'on regarde bien, il y a ici deux dénominateurs qui sont $x$ et $1-{\frac {1}{x}}$. Le premier dénominateur s'annule pour x = 0 et le deuxième s'annule pour x = 1. C'est pour cela que les calculs de f(0) et f(1) ont donné un message d'erreur. Le domaine de définition de la fonction f est donc : $D_{f}=\mathbb {R} -\{0,1\}$

Exemple 2 Soit la fonction g défini par : $g(x)={\sqrt {x-3}}$ Déterminez le domaine de définition de la fonction g Corrigé Nous devons simplement déterminer l'ensemble des nombres réels x pour lesquels le calcul de l'expression ${\sqrt {x-3}}$ est possible. Or, nous savons que dans l'ensemble des nombres réels, les nombres négatifs n'ont pas de racine carrée, on doit donc avoir : $x-3\geqslant 0$ C'est-à-dire : $x\geqslant 3$ Le domaine de définition de la fonction g est donc : $D_{g}=[3;+\infty [$

Dans les deux exemples qui précèdent, nous avons vu qu'il faut veiller à ce que les dénominateurs ne soient pas nuls et que les expressions sous les racines ne soit pas négatives. Dans le cadre de cette leçon, il s'agit des deux seuls cas que nous devons surveiller. Vous verrez par la suite, que la Fonction logarithme n'est définie que pour des valeurs strictement positives, mais comme l'étude de cette fonction est généralement faite après cette leçon, nous n'en parlerons pas ici.

Limites aux bornes du domaine de définition (complément hors programme)

Après avoir déterminé soigneusement de domaine de définition, nous sommes confronté au problème suivant  : Comment va se comporter la fonction si l'on s'approche des bornes du domaine de définition ? Cette question joue un rôle important pour déterminer le tracé de sa courbe représentative. C'est ici qu'intervient le calcul des limites.

Lorsque nous étudions une fonction dans le but de tracer sa courbe représentative, nous devrons systématiquement calculer les limites aux bornes du domaine de définition.

Par exemple, pour le domaine de définition de la fonction f ayant fait l'objet de l'exemple 1 ci-dessus nous avions trouvé :

$D_{f}=\mathbb {R} -\{0,1\}$

Combien de limites devons-nous calculez ?

Tenez-vous bien ! il y a 6 limites à calculer. Pour mieux le voir, nous pouvons réécrire le domaine de définition ainsi :

$D_{f}=]-\infty ;0[\cup ]0;1[\cup ]1;+\infty [$

Nous devons calculer la limite de la fonction f lorsque :

• x tend vers $-\infty$ ;
• x tend vers 0 par valeurs inférieures (à gauche) ;
• x tend vers 0 par valeurs supérieures (à droite) ;.
• x tend vers 1 par valeurs inférieures (à gauche) ;
• x tend vers 1 par valeurs supérieures (à droite) ;
• x tend vers $+\infty$.

(Pour le calcul effectif des limites, se référer à la leçon Limites d'une fonction que nous ne développerons pas ici)

Restriction du domaine d'étude (complément hors programme)

Il se peut que le tracé de la courbe présente certaines symétries. Détecter ces symétries peut nous permettre de simplifier l'étude de la fonction. Si, par exemple, nous déterminons, avant l'étude proprement dite, que le tracé de la courbe est symétrique par rapport à l'axe des ordonnées, il serait superflu d'étudier la fonction pour toutes les valeurs de son domaine de définition alors qu'il suffirait de l'étudier seulement pour les valeurs positives et d'en déduire le reste de l'étude et le tracé de la courbe par symétrie par rapport à l'axe des ordonnées.

Nous allons envisager deux types de symétrie :

• La courbe admet l'axe des ordonnées comme axe de symétrie ;
• La courbe admet l'origine du repère comme centre de symétrie.

Fonction paire

Dans cette leçon, nous adopterons la définition suivante :

Définition

Une fonction sera dite paire si le tracé de sa courbe représentative admet l'axe des ordonnées comme axe de symétrie.

Cette définition étant posée, nous allons essayer de trouver une relation caractérisant les fonctions paires.

Soit une fonction dont le tracé est symétrique par rapport à l'axe des ordonnées (voir le schéma à droite). Choisissons sur l'axe des abscisses deux réels opposés x et -x. Si le tracé de la courbe est symétrique par rapport à l'axe des ordonnées, nous voyons que l'image de x et de -x tombe exactement au même endroit sur l'axe des ordonnées. Nous voyons que nous avons par conséquent f(-x) = f(x). Nous retiendrons :

Propriété

Une fonction f est une fonction paire si et seulement si nous avons la relation suivante :

$\forall x\in D_{f}\qquad f(-x)=f(x)$

(certains cours adoptent comme définition d'une fonction paire la relation énoncée dans la propriété ci-dessus, ce qui rend la compréhension moins immédiate pour beaucoup)

Fonction impaire

Dans cette leçon, nous adopterons la définition suivante :

Définition

Une fonction sera dite impaire si le tracé de sa courbe représentative admet l'origine du repère comme centre de symétrie.

Cette définition étant posée, nous allons essayer de trouver une relation caractérisant les fonctions impaires.

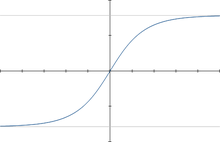
Soit une fonction dont le tracé admet l'origine du repère comme centre de symétrie (voir le schéma à droite). Choisissons sur l'axe des abscisses deux réels opposés x et -x. Si le tracé de la courbe est symétrique par rapport à l'origine du repère, nous voyons que l'image de x et de -x tombe sur deux valeurs opposées sur l'axe des ordonnées. Nous voyons que nous avons par conséquent f(-x) = -f(x). Nous retiendrons :

Propriété

Une fonction f est une fonction impaire si et seulement si nous avons la relation suivante :

$\forall x\in D_{f}\qquad f(-x)=-f(x)$

(certains cours adoptent comme définition d'une fonction impaire la relation énoncée dans la propriété ci-dessus, ce qui rend la compréhension moins immédiate pour beaucoup)

Quelques propriétés des fonctions paires et impaires

Nous avons les propriétés suivantes :

• Une fonction polynôme n'ayant que des monômes de puissance paire est une fonction paire.
• Une fonction polynôme n'ayant que des monômes de puissance impaire est une fonction impaire.
• Le produit ou le quotient de deux fonctions paires est une fonction paire.
• Le produit ou le quotient de deux fonctions impaires est une fonction paire.
• Le produit ou le quotient d'une fonction paire par une fonction impaire est une fonction impaire.
• La racine carrée d'une fonction paire positive est une fonction paire.

Les propriétés précédentes sont facile à démontrer. Nous invitons le lecteur à le faire à titre d'exercices.

Les propriétés précédentes permettent de voir rapidement si une fonction est paire ou impaire mais ne sont généralement pas au programme. On ne peut donc pas s'en contenter pour étudier la parité d'une fonction. voir la façon correcte de procéder dans l'exemple ci-dessous.

Exemple Soit la fonction f définie par : $f(x)={\frac {x^{3}-x}{\sqrt {x^{2}+3}}}$ Étudiez la parité de la fonction f Corrigé Le numérateur est un polynôme impair car n'ayant que des monômes de puissance impaire. Sous la racine du dénominateur, il y a un polynôme pair car formé de monômes de puissance paire (La constante 3 est considéré comme monôme de puissance paire car pouvant s'écrire 3x0). La racine carrée d'une fonction paire est une fonction paire donc le dénominateur est une fonction paire. On effectue donc le quotient d'une fonction impaire par une fonction paire. Ce qui donne finalement une fonction impaire. Nous savons donc que f est une fonction impaire. Si cette façon de procéder n'est pas au programme, cela nous permet tout de même de savoir que nous devons démontrer que $f(-x)=-f(x)$ Nous écrirons donc sur notre copie : ${\begin{aligned}\forall x\in \mathbb {R} \qquad f(-x)\,&=\,{\frac {(-x)^{3}-(-x)}{\sqrt {(-x)^{2}+3}}}\\&=\,{\frac {-x^{3}+x}{\sqrt {x^{2}+3}}}\\&=\,-{\frac {x^{3}-x}{\sqrt {x^{2}+3}}}\\&=\,-f(x)\end{aligned}}$ donc f est une fonction impaire.

Asymptotes (complément hors programme)

Nous adopterons la définition suivante qui n'est pas la plus générale mais qui est suffisante dans le cadre de cette leçon.

Définition

Soit une courbe C représentative d'une fonction f. On dira qu'une droite D est une asymptote à la courbe C si la distance d'un point A de la courbe C à la droite D tends vers 0 lorsque l'on fait tendre l'abscisse de M vers une borne du domaine de définition

Nous pouvons, par exemple, imager la visualisation d'une asymptote lorsque x tends vers $+\infty$

(Sur l'animation, le point A se projette verticalement en B sur l'asymptote et nous voyons que la distance ${\overline {AB}}$ tend vers 0 lorsque l'abscisse du point A tend vers $+\infty$)

Bien que la distinction soit théoriquement superflue, nous distinguerons, dans le cadre de cette leçon, trois types d'asymptotes. Nous avons :

• Les asymptotes horizontales qui sont des droites parallèles à l'axe des abscisses.
• Les asymptotes verticales qui sont des droites parallèles à l'axe des ordonnées.
• Les asymptotes obliques qui ne sont parallèles ni à l'axe des abscisses, ni à l'axe des ordonnées.

• 
  Asymptote horizontale en $+\infty$
• 
  Asymptote verticale en x = -2 et asymptote horizontale en y = 1 commune en $+\infty$ et $-\infty$
• 
  Asymptote oblique
• 
  Asymptote oblique coté $+\infty$ et axe des abscisses comme asymptote horizontale coté $-\infty$ et aussi axe des ordonnées comme asymptote verticale en x = 0
• 
  Asymptote oblique commune au branche en $+\infty$ et $-\infty$ et aussi axe des ordonnées comme asymptote verticale en x = 0
• 
  Deux asymptotes horizontales en $+\infty$ et $-\infty$

nous allons détailler ci-dessous comment déterminer les trois types d'asymptotes.

Asymptotes horizontales

Supposons que lorsque l'on fait tendre x vers $+\infty$ (ou vers $-\infty$), on obtienne une limite fini l, nous voyons alors que le tracé de la courbe a tendance à prendre des valeurs de plus en plus proche de l. Ce qui signifie que le tracé de la courbe a tendance à être de plus en plus horizontal et par conséquent à s'approcher d'une droite horizontale d'équation y = l.

Nous retiendrons donc la propriété suivante :

Propriété

Soit f une fonction vérifiant l'une des deux propriétés suivantes :

$\lim _{x\to \infty }f(x)=l$

ou

$\lim _{x\to -\infty }f(x)=l$

alors la droite d'équation y = l est une asymptote horizontale à la courbe.

Démonstration

Supposons :

$\lim _{x\to \infty }f(x)=l$

et considérons la droite d'équation y = l. On a alors :

$\lim _{x\to \infty }(f(x)-y)=lim_{x\to \infty }(f(x)-l)=l-l=0$

Nous voyons que la distance verticale $|f(x)-l|$ entre la courbe et la droite d'équation y = l tend vers 0 lorsque x tend vers l'infini, ce qui montre que la droite d'équation y = l est bien une asymptote horizontale.

Démonstration identique en faisant tendre x vers $-\infty$

 

Asymptotes verticales

Supposons que lorsque l'on fait tendre x vers une valeur particulière a (par valeur supérieure ou inférieure), la fonction tende vers $+\infty$ ou vers $-\infty$. Si, par exemple, elle tend vers $+\infty$, nous voyons que le tracé de la courbe va monter en tendant de plus en plus vers une droite verticale. Nous arrivons ainsi facilement à imaginer que la courbe représentative va avoir une asymptote verticale d'équation x = a.

Nous retiendrons donc la propriété suivante :

Propriété

Soit f une fonction vérifiant l'une des quatre propriétés suivantes :

$\lim _{x\to a^{+}}f(x)=+\infty$

ou

$\lim _{x\to a^{-}}f(x)=+\infty$

ou

$\lim _{x\to a^{+}}f(x)=-\infty$

ou

$\lim _{x\to a^{-}}f(x)=-\infty$

alors la droite d'équation x = a est une asymptote verticale à la courbe.

Démonstration

Démonstration évidente car la distance horizontale d'un point M d'abscisse x à la droite verticale dont tous les points ont pour abscisse a, est la valeur $|x-a|$ qui, par hypothèse, tend vers 0.

 

Asymptotes obliques

Si la courbe représentative de la fonction admet une asymptote oblique cela signifie que son tracé se rapproche d'un droite d'équation y = ax + b. cela signifie aussi que la différence entre la courbe et l'asymptote oblique tend vers 0 lorsque l'on fait tendre x, soit vers $+\infty$, soit vers $-\infty$. Nous auront donc :

$\lim _{x\to \infty }\left[f(x)-(ax+b)\right]=0$

C'est cette limite que nous devrons calculer si l'on nous demande de démontrer que la droite d'équation y = ax + b est une asymptote.

Propriété

La droite d'équation $y=ax+b$ est une asymptote oblique à la courbe représentative d'une fonction f si et seulement si :

$\lim _{x\to +\infty }\left[f(x)-(ax+b)\right]=0$

ou

$\lim _{x\to -\infty }\left[f(x)-(ax+b)\right]=0$

Il peut arriver (cela dépend des programmes) que l'on ne nous donne pas l'équation de l'asymptote. C'est donc à nous de déterminer la valeur de a et b.

Pour calculer la valeur de a nous avons la propriété suivante :

Propriété

Si la droite d'équation $y=ax+b$ est une asymptote oblique à la courbe représentative d'une fonction f alors la valeur de a est donnée par :

$a=\lim _{x\to +\infty }{\frac {f(x)}{x}}$

ou

$a=\lim _{x\to -\infty }{\frac {f(x)}{x}}$

selon que l'on cherche une asymptote oblique coté $+\infty$ ou coté $-\infty$.

Démonstration

Si y = ax + b est une asymptote oblique coté $+\infty$, nous avons :

$\lim _{x\to +\infty }\left[f(x)-(ax+b)\right]=0$

qui s'écrit :

$\lim _{x\to +\infty }\left(f(x)-ax-b\right)=0$

et si l'on divise tous les termes par x, on obtient :

$\lim _{x\to +\infty }\left({\frac {f(x)}{x}}-a-{\frac {b}{x}}\right)=0$

Comme :

$\lim _{x\to +\infty }{\frac {b}{x}}=0$

il nous reste :

$\lim _{x\to +\infty }\left({\frac {f(x)}{x}}-a\right)=0$

d'où l'on déduit:

$a=\lim _{x\to +\infty }{\frac {f(x)}{x}}$

Démonstration similaire coté $-\infty$.

 

Une fois que nous avons calculé la valeur de a et seulement après avoir calculé la valeur de a, nous avons la propriété suivante pour calculer la valeur de b :

Propriété

Si la droite d'équation y = ax + b est une asymptote oblique à la courbe représentative d'une fonction f alors la valeur de b est donnée par :

$b=\lim _{x\to +\infty }\left(f(x)-ax\right)$

ou

$b=\lim _{x\to -\infty }\left(f(x)-ax\right)$

selon que l'on cherche une asymptote oblique coté $+\infty$ ou coté $-\infty$.

Démonstration

Si y = ax + b est une asymptote oblique coté $+\infty$, nous avons :

$\lim _{x\to +\infty }\left[f(x)-(ax+b)\right]=0$

qui s'écrit :

$\lim _{x\to +\infty }\left(f(x)-ax\right)=b$

Démonstration similaire coté $-\infty$.

 

Parfois, il se peut que l'on arrive à calculer a mais que l'on n'arrive pas ensuite à calculer b car la limite concernée diverge vers $+\infty$ ou $-\infty$. Dans ce cas, nous dirons que la courbe admet une direction asymptotique.

Position relative de deux courbes

Supposons que nous ayons deux courbes à tracer dans un même repère correspondant respectivement à deux fonctions f et g. Nous pouvons alors souhaiter savoir laquelle des deux courbes est en dessus de l'autre. Et si les deux courbes s'interceptent, nous souhaiterons peut-être connaître les abscisses des points d'interception des deux courbes ou pour quelles valeurs de x l'une des deux est en dessus de l'autre et pour quelle valeurs de x, elle est en dessous. Comment procéder ?

En fait, ce n'est pas très compliqué, il suffit d'étudier la différence :

$f(x)-g(x)$

pour toutes valeurs de x.

Nous voyons que si, pour une valeur de x, cette différence est positive, cela signifie que f(x) est plus grand que g(x) (le tracé de f est dessus le tracé de g) et si pour une valeur de x cette différence est négative, alors f(x) sera plus petit que g(x) (le tracé de f est dessous le tracé de g). Nous voyons aussi que si pour une valeur de x, la différence est nulle, cela signifie que f(x) = g(x) et pour cette valeur de x, les courbes se coupent.

Pour étudier la position relative de deux courbes, nous ferons donc une étude de signe de la différence f(x) - g(x).

Un cas particulier intéressant survient lorsque le tracé de la courbe admet une asymptote. Nous avons vu plus haut que, dans ce cas, le tracé de la courbe se rapproche de l'asymptote quand x tend vers $+\infty$ ou quand x tend vers $-\infty$. Ce que nous n'avons pas encore précisé, c'est de savoir si le tracé de la courbe tend vers l'asymptote par en dessus ou par en dessous. Sur le schéma de droite, nous avons représenté deux situations possibles (parmi d'autres). Nous avons une asymptote oblique croissante (en vert sur le dessin). Nous voyons que la courbe A commence par couper l'asymptote en W et tend ensuite vers l'asymptote par en dessus alors que la courbe B tend vers l'asymptote par en dessous. Comment différencier ces deux situations. La dérivée ne nous permettra pas de différencier ces deux situations car dans les deux cas, les courbes sont croissantes, ce qui entraîne que la dérivée est positive.

Pour différencier ces deux cas, nous allons appliquer ce que nous avons dit ci-dessus en considérant l'asymptote comme étant le tracé de la courbe correspondant à la fonction g. Plus précisément, si y = ax + b est l'équation de l'asymptote, nous allons étudier le signe de la différence :

$f(x)-y=f(x)-(ax+b)$

• Pour les valeurs de x qui rendront cette différence positive, la courbe sera en dessus de l'asymptote.
• Pour les valeurs de x qui rendront cette différence négative, la courbe sera en dessous de l'asymptote.
• Pour les valeurs de x qui rendront cette différence nulle, la courbe coupera l'asymptote.