Recherche:Le temps dans la relativité restreinte ou la célérité du temps/Relativité restreinte et dualité
La légitimité de ce chapitre est basée sur la notion logique suivante : un évènement a lieu relativement au même 'endroit' et au même temps quel que soit l'espace considéré.
LIEN MATHEMATIQUE
Considérons classiquement deux observateurs (O) et (O') en mouvement rectiligne uniforme l'un par rapport à l'autre et initialement confondus. Un même évènement peut être décrit spatialement et temporellement par les équations de Lorentz dans leurs référentiels galiléens respectifs :
On a :
1) x' = ɣ ( x - V.t ) 2) x = ɣ ( x' + V.t' )
y' = y y = y'
z' = z z = z'
3) t' = ɣ ( t - V.x/c² ) 4) t = ɣ ( t' + V.x'/c² )
Maintenant, considérons l'expérience de simultanéité de ce chapitre. Les conditions de départ nous permettent de relier le temps d'un observateur du laboratoire (O) au temps d'un observateur du vaisseau (O') par l'équation simple t = ɣ t'. En effet, empiriquement et théoriquement, des 'objets' en mouvement dans notre espace-temps sont sont soumis à la dilatation temporelle. De plus, relativement au concept de déplacement du temps ou de l'espace, l'univers étant contracté pour le vaisseau sans l'être pour le laboratoire, le temps met moins de 'temps' pour parvenir à l'observateur du vaisseau qu'à celui du laboratoire. Théoriquement, il est impossible de déterminer quel objet est en déplacement, il faut donc l'établir (le fixer).
L'autre distinction de la théorie à l'égard de l'expérience est que les objets théoriques sont ponctuels. Si l'on considère que l'objet est fini, la dualité apparait théoriquement.
- Si on impose t = ɣ t' dans 4), on obtient Vx'/c² = 0, soit V = 0: Résultat à priori surprenant mais identique à celui nécessaire pour obtenir une cohérence spatiale (Voir plus loin).
- En imposant V = 0 dans 2), on obtient x = ɣ x'. L'espace est contracté suivant l'axe de déplacement à l'extérieur du vaisseau (Rien de nouveau, si ce n'est que l'on obtient une contraction des longueurs pour une vitesse nulle)
- Si on impose t = ɣ t' dans 3) :
t' = ɣ² t'² - ɣ V x / c²
t' (1 - ɣ²) = - ɣ V x / c²
t' (1 - c² / (c² - V²)) = - V x ( c² / ( c² - V²))/ c²
Après simplification : t' = x / ɣ V
x = ɣ.V.t' soit x = V.t, le vaisseau continue de se déplacer dans l'espace-temps du laboratoire.
Considérons l'invariant relativiste classique x² + y² + z² - c².t² = x'² + y'² + z'² - c².t'²; comme t = ɣ.t', on a (x² + y² + z²) = ɣ².(x'² + y'² + z'²). Cette relation doit être vraie pour l'observateur du laboratoire comme pour celui du vaisseau. L'expérience du chapitre 3 (géométrie) est démonstrative pour l'observateur du vaisseau. En revanche, l'expérience symétrique pour l'observateur du vaisseau conduit à un paradoxe (jumeaux).
Comme x = ɣ.x’, on a (y² + z²) = ɣ². (y'² + z'²)
Par symétrie, pour l'observateur du vaisseau, nous déduisons que y = ɣ . y’ et z = ɣ . z’. Or, pour rappel, y = y' et z = z' pour l'observateur du laboratoire. Pour le vaisseau l'espace extérieur est réduit d'un facteur ɣ dans toutes les directions.
Le vaisseau doit être plus gros et immobile pour que l'invariant relativiste soit réciproquement égal. C'est l'essence de la dualité. C'est l'origine des ondes.
Mais, comment un évènement peut être a un endroit pour un observateur et décalé pour l'autre ? C'est ce que propose d'expliquer le 'lien physique' à venir
LIEN PHYSIQUE, LOGIQUE ET GEOMETRIQUE
Expérience de pensée fondamentale
Le but des deux expériences de pensée suivantes, consiste à démontrer l'existence de 2 réalités différentes pour deux observateurs différents. Le premier, à l'extérieur voit l'autre comme une 'particule'. L'autre à l'intérieur se perçoit comme une 'onde'
Observateur extérieur :
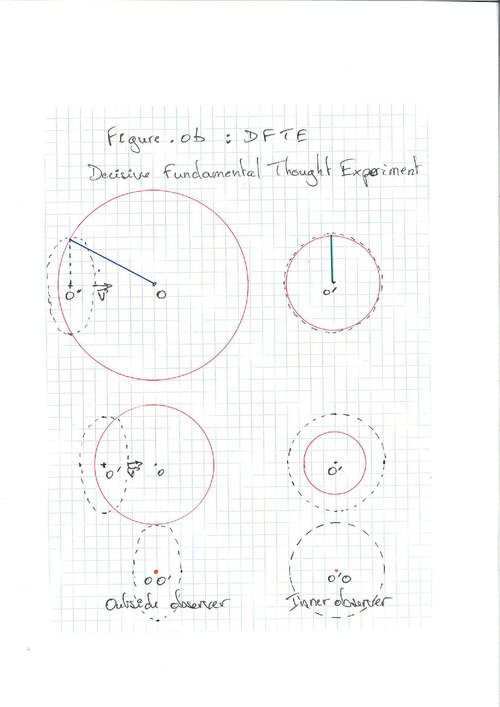
Considérons un vaisseau sphérique se déplaçant à une vitesse V = Ѵ3/2c, de sorte que ɣ = 2. (fig. 0a).



Plusieurs lasers sont disposés dans la structure. À des fins de simulation, il y en a 12.
Pour l’observateur intérieur, situé au centre du navire, les lasers se déclenchent «simultanément». Les points de départ des lasers forment une figure sphérique comme la coque dans l’espace de l’observateur intérieur . Nous l’appellerons «onde».
Pour l’observateur extérieur, c’est moins simple. Le navire est plus petit, non sphérique et mobile. Nous l’appellerons «particule». Les départs des lasers sont classiquement dictés par la règle d’invariance de la vitesse de la lumière. Ils définissent une sphère aplatie composée de croix rouges et décentrée (O'''). Le phénomène observé est soigneusement décrit dans la littérature classique. Notre interprétation singulière est développé dans les chapitres précédents.
Observateur intérieur : expérience de pensée fondamentale et décisive (EPFD).
Dans cet article, nous focalisons notre étude sur l'onde. C’est là que réside la différence la plus notable avec l’interprétation physique classique. Une expérience de pensée judicieuse et simple permet d'appréhender la notion d'onde.
Considérons une sphère de photons convergents vers un observateur O fixe de notre espace-temps (fig.0b). Considérons un observateur ponctuel O' se déplaçant à une vitesse V = Ѵ3/2c de sorte que O et O' coïncident lorsque les photons se croisent. L'expérience n'est rien d'autre qu'une application dynamique de l'invariant relativiste (x² + y² + z² - c².t² = x'² + y'² + z'² - c².t'²). Pour l'observateur extérieur (O), x²+y²+z²=c²t². Pour l'observateur intérieur (O'), x'²+y'²+z'²=c²t'². O' se déplaçant dans l'espace-temps de O, leurs temps sont reliés par la dilatation temporelle, on a t(O) = ɣ t'(O'). Ainsi, mathématiquement, la sphère des évènements ou photonique est ɣ fois plus grande pour l'observateur extérieur (O) que pour l'observateur intérieur (O').
Maintenant, considérons que O' est le centre du vaisseau sphérique de rayon Ro soumis à l'expérience de pensée initiale. Dans le référentiel de O', les lasers parcourent Ro avant de se croiser. Par contre, en application de EPFD, ces mêmes lasers proviennent tous de ɣRo dans le référentiel de O. Or, O et O' étant confondus, l'espace de O est contracté d'un facteur ɣ dans toutes les directions à l'intérieur du vaisseau pour O', c'est l'onde.
Par abus de langage et pour comprendre : Tous les photons parvenant en O et O' simultanément ont parcouru Ro à l'intérieur du vaisseau ou ɣRo dans notre espace. En effet, tous les photons se croisant simultanément formaient obligatoirement une sphère au préalable. Ainsi, il suffit de connaître un unique rayon pour définir toute la sphère. Or nous en connaissons un: celui du photon émanant du sommet du vaisseau (pythagore). En conséquence, notre espace est obligatoirement contracté dans toutes les directions à l'intérieur du vaisseau pour un de ses observateurs: c'est l'onde.
Par contre, pour l'observateur extérieur, le vaisseau est plus petit, se déplace et les évènements ne sont plus simultanés. Si l'on reprend l'expérience de pensée de la fig.0b. Si l'on considère que O' est le centre d'un objet fini, la sphère commence par pénétrer par la gauche, puis par les sommets, puis par la droite
D'où viennent les photons ?
Concept:
Avant d’aller plus loin, il y a un concept simple qu’il est fondamental de comprendre. L’origine relative d’un photon dans un espace pour un observateur par rapport à un autre espace permet de caractériser dans cette direction cet espace par rapport à l’autre. Par exemple, si un photon vient de plus loin dans un espace que dans un autre, cela signifie que cet espace est dilaté par rapport à l’autre dans la direction spécifique. A l’inverse, un observateur de l’autre espace percevra le premier contracté. Appliquons cette idée à la figure.
Application du concept à la figure:
Considérons l’axe des abscisses. Pour l’observateur O''' de la particlonde, dans notre espace, le laser de l’arrière provient d’un facteur a = (c + V) / c plus loin que pour l’observateur O'' de l’onde. Ainsi, pour l’observateur du vaisseau spatial, l’espace est contracté dans la direction opposée au déplacement. Par conséquent, tout est plus proche. A l’inverse, le laser à l’avant provient d’un facteur b = (c – V) / c plus proche. Ainsi, dans le sens du déplacement, l’espace est dilaté. Tout est plus loin pour l’observateur du vaisseau. Ces facteurs sont mathématiquement cohérents. Ainsi:
a x b = (c – V) x (c + V) / c² = (c² - V²) / c² = 1 / (1 – V² / c²) = ɣ²
Le long de l’axe des abscisses, l’espace est globalement contracté d'un facteur gamma comme dans la théorie classique. Cependant, cette contraction est asymétrique. Nous savons que x' = ɣ ( x - V.t ). Ɣ et V étant constants, t est asymétrique. Comme le vaisseau est symétrique (sphère) dans son espace-temps, l’asymétrie du temps compense exactement l’asymétrie induite par l’invariance de la lumière pour la particlonde. En raison de cette asymétrie, la position de l’observateur dans son espace change la nature de l'expérience de pensée. Ce concept est largement discuté dans la partie à venir et celle sur le modèle novateur.
Maintenant, considérons le laser émanant du haut du navire (ligne verte) comme dans l’expérience de pensée la plus courante (pythagore). Sa trajectoire est droite et verticale pour l’observateur du navire alors qu’elle est inclinée pour l’observateur extérieur. Pour le navire, la trajectoire coïncide avec l’axe des ordonnées alors que ce même axe est incliné pour l’observateur extérieur. On commence à appréhender pourquoi y = ɣ. y' pour l’onde et y' = y pour la 'particule'. Appliquons le même concept que pour l’axe des abscisses. Comme O''y'' est vertical et par application du concept, le laser vient verticalement de ɣ fois plus loin (Pythagore). En conséquence, l’espace est contracté le long de l’axe des ordonnées pour O''.
La particlonde, immobile comme l'onde, est la projection du vaisseau de son espace-temps dans le nôtre. Pour revenir à l’onde, il suffit de faire la transformation inverse de la particlonde grâce au concept du photon. Ainsi fait, dans son espace-temps, le vaisseau est sphérique, notre espace-temps est contracté par un facteur gamma à l’intérieur dans toutes les directions. Le navire est une onde et Ɣ fois plus grande.
Comment progresse l'onde?
Reste une question importante : comment le vaisseau avance dans son espace-temps puisqu’il est stationnaire? L’explication nécessite un nouvel article. En bref, les événements qui se produisent au même « moment » pour un observateur sont un État. Pour se déplacer, l’observateur change d’état. La particule est la superposition de ces états. La notion de fréquence apparaît en filigrane.
Les 2 expériences de pensée à venir servent à identifier l'incohérence spatiale de l'interprétation physique classique:
Première expérience de pensée classique cohérente
Considérons l'expérience de simultanéité du chapitre 3 d'un vaisseau se déplaçant à V = Ѵ3/2c. Intéressons nous à la localisation des points de départ des lasers du vaisseau.
Dans l'espace-temps du vaisseau, les départs sont simultanés, la figure est circulaire comme la coque (fig10a), on parlera de grand vaisseau. L'espace-temps du vaisseau étant contracté, le cercle devient une ellipse dilatée dans l'espace-temps du laboratoire.
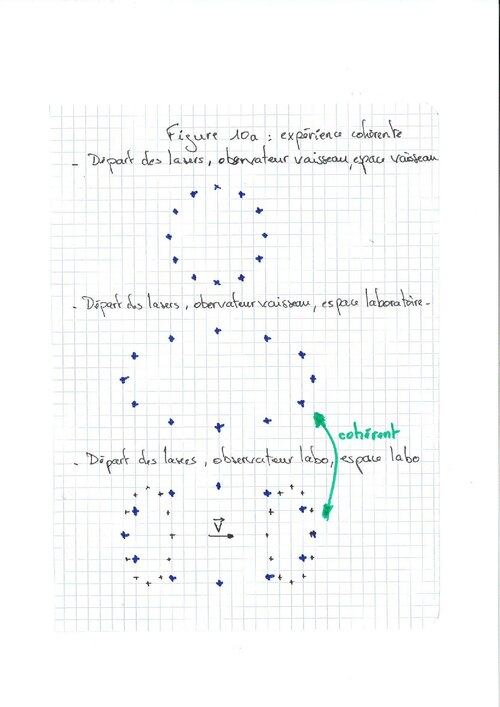
Dans l'espace-temps de l'observateur extérieur, le vaisseau est une ellipse contractée, on parlera de petit vaisseau. Toutefois, en raison de la vitesse et de la non-simultanéité, les départs de laser représentent une ellipse dilatée, identique à celle de l'expérience de pensée précédente. Le résultat est cohérent, l'origine des lasers est au même endroit quel que soit l'espace-temps considéré.
Deuxième expérience de pensée classique incohérente
Maintenant, considérons une expérience de simultanéité inverse. Un laboratoire sur terre de forme circulaire est équipé du même protocole expérimental. L'observateur extérieur est dans le vaisseau.
Dans l'espace-temps du laboratoire, les départs sont simultanés, la figure est circulaire (fig10b).
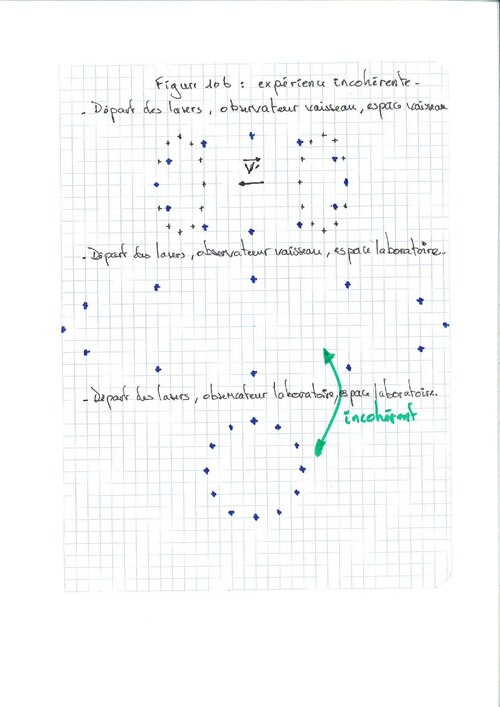
Dans l'espace-temps de l'observateur extérieur (vaisseau), le laboratoire est une ellipse contractée. En raison de la vitesse et du principe classique de non-simultanéité, les lasers représentent une ellipse dilatée. Or, cet espace-temps étant contracté, la figure, après transformation dans l'espace du laboratoire est une ellipse doublement dilatée. Ainsi, il y a un facteur ɣ² spatial entre les deux représentations. Le résultat est incohérent, la position de l'origine des lasers n'est pas identique dans les deux espace-temps. Derrière cette impossibilité physique, se cache le principe même de la dualité onde-corpuscule.
Postulat de réciprocité des vitesses
Le formalisme de la relativité restreinte est mathématique. Si une incohérence physique ou géométrique existe, elle est obligatoirement inhérente au postulat de réciprocité des vitesses.
Explication : Si, estimer qu'un objet qui se déplace par rapport à un autre à une vitesse V dans un espace mathématique revient au même que considérer le mouvement inverse à une vitesse -V. Il en va tout autrement dans un espace physique ou la notion de position prend tout son sens. Ainsi, une fois que les équations sont établies mathématiquement par symétrie, il est nécessaire d'imposer à tout le système une translation de +V pour que tous les objets se retrouvent physiquement au même endroit.
Cohérence spatiale
La première expérience conduit à une situation cohérente. Aussi, nous validons et conservons le concept classique. Ainsi, par hypothèse, le vaisseau est correctement défini dans le repère de l'observateur extérieur (laboratoire). Trivialement, le vaisseau et le laboratoire sont correctement définis dans leurs repères propres, ceux sont des sphères. Pour rendre l'expérience de pensée 2 cohérente, il faudrait que le départ des lasers soit relativement une sphère dans le référentiel du vaisseau comme dans son référentiel propre (fig 11).
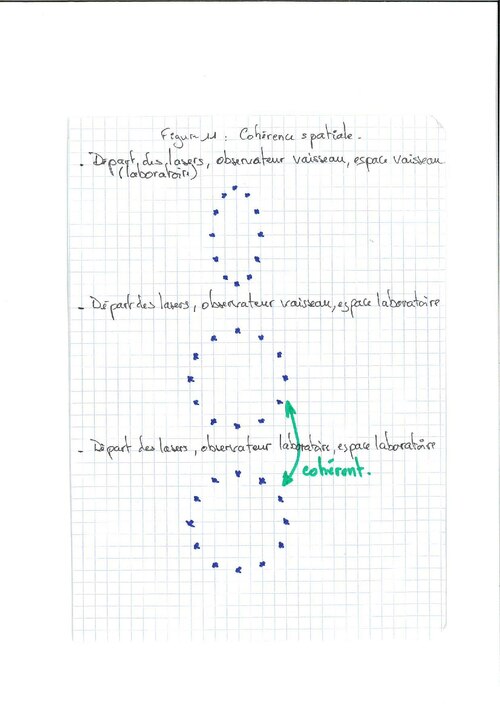
Pour ce faire, la seule solution physiquement congrue est que la vitesse du laboratoire soit nulle dans le repère du vaisseau (V'=0). Son application simple engendre deux difficultés et deux facilités. La première facilité est la cohérence spatiale. La deuxième facilité est d'éluder la problématique de la courbure de l'espace-temps : le petit vaisseau parcourt la distance du grand vaisseau qui est immobile. Pour les difficultés, il n'y a plus de cohérence temporelle et le vaisseau n'avance plus.
Cohérence temporelle
En vertu de la célérité du temps, pour qu'une même durée soit relativement augmentée dans l'espace du vaisseau en comparaison de celle du laboratoire, il est nécessaire que le vaisseau soit relativement plus grand que le laboratoire dans l'espace du laboratoire. Inversement, pour qu'une même durée soit relativement plus petite dans l'espace du laboratoire en comparaison de celle du vaisseau, il est nécessaire que le laboratoire soit relativement plus petit que le vaisseau dans l'espace du vaisseau. Or, dans la première expérience, les ellipses représentatives des départs de laser sont identiques. (fig12, Explication : si le laboratoire est plus petit que le vaisseau et qu'il ne bouge pas, la lumière met moins de temps pour traverser le plus petit.)