Recherche:Flou stroboscopique

Flou stroboscopique

Travaux de recherche en sciences de l'ingénieur

---

Toute réaction ou commentaire par rapport à ce travail de recherche sont les bienvenus sur cette page de discussion.

---

Cette page fait partie de l’espace recherche de Wikiversité et dépend de la faculté sciences de l'ingénieur. Pour plus d'informations, consultez le portail de l'espace recherche ou rendez-vous sur l'index des travaux de recherche par faculté.

Synthèse additive flou cinétique linéaire ou flou stroboscopique 3D Blanc Magenta Jaune Cyan

Le flou stroboscopique 3D ou flou cinétique linéaire ou rectiligne

Animation flou stroboscopique 3D rectiligne, photos en 256 couleurs prises à 1/40s pour un angle par dichotomie de pi/3

Modèle statuette d'argile pour flou stroboscopique 3D rectiligne

Modele Synthese additive 3D aux couleurs RVB

Flou stroboscopique formule originale

Le flou stroboscopique

Kinematic de typographie stroboscopique

Le flou stroboscopique est un flou reproduit à partir d'un mouvement circulaire uniforme d'après la relation entre vitesse angulaire et linéaire.

Temps angulaire

https://upload.wikimedia.org/wikipedia/commons/e/e9/Flou_stroboscopique_typographie_kinematic.mpg

• Fonction angulaire calculée d'après la formule tempsdepause(pi/4;45tr/mn)=1/6s

t(θ) = exp[(4θ-$\pi$)/24)]/6

t(0)= exp[(-$\pi$)/24)]/6

• Dérivée

t'(θ) = exp[1$*$4/24]/6 = exp[1/6]/6

• Linéarisation du temps de pause t$_{\theta }$par rapport à l'angle θ

t$_{0}$=exp[(-$\pi$)/24)]/6

t$_{\theta }$ = t$_{0}$$\exp(it)$$^{2}$$^{\pi }$= t$_{0}$$*$(cos(t)̹̹$+$isin(t))$^{2}$$^{\pi }$= $\exp$[(-$\pi$)/24]/6 $*$(cos(t)̹̹$+$isin(t))$^{2}$$^{\pi }$

• Primitive

T(θ) = (1/12)$*$exp(1/6)$*$θ² + (1/6)$*$exp(-$\pi$/24)$*$θ + ($\pi$/3)$*$(exp(-$\pi$/24)+$\pi$$*$exp(1/6))

• Fonction inverse

t-¹(θ) = t($\pi$-3)

Exemple de ce qu'on peut faire avec la vitesse angulaire d'après le théorème de l'addition des vitesses de la mécanique relativiste d'Albert Einstein, la sonde pitot numérique:

$Vitesse={\sqrt {\mid vitesseangulairedelarotationdelaterre*{\frac {radians(longitudeB-LongitudeA)}{secondes(TempsB-tempsA)}}\mid +({\frac {radians(latitudeB-latitudeA)}{secondes(tempsB-tempsA)}})^{2}}}*(rayonmoyendelaterre+altitudeB)$

« Ce n'est pas le Soleil qui tourne autour de la Terre,

c'est la Terre qui tourne autour du Soleil,

Et pourtant la Terre elle tourne sur elle-même,

c'est pour cela qu'elle est ronde… »

Par cette formule pour un vol New York - Paris à 4000 m au-dessus de la mer et à 630,6 hectoPascal pour -8,5°°, un avion A320 de 76,4928 tonnes avec un angle d'horizon artificiel de -1,566923607° qui mettra 7h15 aura une vitesse moyenne de 807,244837279434 km/h comme les distances en avion rallongent et consommera une valeur énergétique de 1,92307451971865 Gigajoules contre 1,63767263702058 Gigajoules pour le vol retour Paris New York d'une durée de 8h30 à une vitesse de 744,9390928139391 km/h et avec un angle d'horizon artificiel de -1,567222514° comme les distances raccourcissent avec la terre qui tourne sur elle-même selon la relativité d'Albert Einstein

Si la Terre était complètement sphérique et bien lisse il faudrait 3,651898169 jours pour qu'un ballon de basket roulant à 314662.519 km/h fasse le tour de la Terre en passant par les pôles.

Masse d'un avion en vol=(Masse volumique de l'atmosphere)*Altitude*Surface ventrale*Cx du fabricant

$Masseavion=\left({\frac {Massemolairedel'air*PressionatmospheriqueB}{CstUnivGpR*TemperatureB}}\right)*AltitudeA*Surfaceprojetee*CoefCx$

$Horizonartificiel=\arctan \left({\frac {\left({\frac {Massemolairedel'air*PressionatmospheriqueB}{CstUnivGpR*TemperatureB}}\right)*AltitudeA*Surfaceprojetee*CoefCx*g}{{\sqrt {\mid vitesseangulairedelarotationdelaterre*{\frac {radians(longitudeB-LongitudeA)}{secondes(TempsB-tempsA)}}\mid +({\frac {radians(latitudeB-latitudeA)}{secondes(tempsB-tempsA)}})^{2}}}*(rayonmoyendelaterre+altitudeB)}}\right)$

Masse de la lune=384399000*PI*1737400^2*0,5=1,822643624*10^21 kg

Masse volumique du vide sidéral aux alentours de la Lune=40,38090554 kg/m^3 nettement inférieur à la masse volumique de l'eau(997kg/m^3) et légèrement supérieur à la masse volumique de l'air (1,2kg/m^3)

$Massed'unphoton={\frac {ConstantedePlanck*frequenceduphoton}{vitessedelalumieredanslevide^{2}}}$

masse d'un photon orange déplaçant une minuscule masse d'air à la vitesse de la lumière=1,491520911*10^-36 kg

$$Frequenced'unphoton=\left({\frac {vitessedelalumieredanslevide}{(ConstantedeGladstonedale*massevolumiquedel'air+1)*longueurdondeduphoton}}\right)$$

fréquence d'un photon orange= 202,30876655 THertz

$Intensited'unphotonderriereuneepaisseur=Intensitedevant*\exp \left({\frac {-4\pi *CstedeGladstoneDale*epaisseurencm}{longueurdondeduphoton}}\right)$

Soit pour un photon orange d'intensité 1KiloWatt devant aura derrière une épaisseur de 1 nanomètre d'air une intensité lumineuse de 76,9026362586509 Watts

ex vitesse orbitale de la lune par rapport à la vitesse de rotation de la terre =(RACINE(ABS(0,00007292115×RADIANS(185−187)÷(420))+PUISSANCE(RADIANS(22−22)÷(420);2)))×(383623000)*3,6=107513,482389629 km/h

En python pour déterminer instantanément la vitesse d'un point par rapport à la terre on fait le programme suivant en faisant l'analyse du champ lexical séparé par une virgule de deux trames GNGGA précédente et suivante et où on fait comme sur une feuille de calcul la formule dans une boucle tant que en accédant aux valeurs du dictionnaire pour les longitudes, latitudes, altitudes et le temps:

""" GNGGA

Compteur de vitesse par rapport au mouvement de rotation de la terre

"""

import serial

import math

# Set up serial:

ser = serial.Serial(

    port='/dev/ttyACMx',\

    baudrate=9600,\

        timeout=1)

# Helper function to take HHMM.SS, Hemisphere and make it decimal:

def degrees_to_decimal(data, hemisphere):

    try:

        decimalPointPosition = data.index('.')

        degrees = float(data[:decimalPointPosition-2])

        minutes = float(data[decimalPointPosition-2:])/60

        output = degrees + minutes

        if hemisphere == 'N' or hemisphere == 'E':

            return output

        if hemisphere == 'S' or hemisphere == 'W':

            return -output

    except:

        return ""

   

def parse_GNGGA(data):

    data = data.split(',')

    dict = {

            'fix_time': data[1],

            'latitude': data[2],

            'latitude_hemisphere' : data[3],

            'longitude' : data[4],

            'longitude_hemisphere' : data[5],

            'fix' : data[6],

            'sat' : data[7],

            'dop' : data[8],

            'altitude' : data[9],

            'unit_alt' : data[10],

            'WGS84' : data[11],

            'unit_wgs84' : data[12],

            'vide' : data[13],

            'checksum' : data[14]

   

            }

   

    dict['decimal_latitude'] = degrees_to_decimal(dict['latitude'], dict['latitude_hemisphere'])

    dict['decimal_longitude'] = degrees_to_decimal(dict['longitude'], dict['longitude_hemisphere'])

    return dict

   

# Main program loop:

gpsDataB = None

speedA= 0.0 

masse= 90.0

while True:

 

   

    line = str(ser.readline())

   

    if "b'$GNGGA" in line :

        gpsDataA = parse_GNGGA(line)

       

        if gpsDataB is not None:

           

            AltA= float(gpsDataA.get('altitude'))

            AltB= float(gpsDataB.get('altitude'))

            LonA=float(gpsDataA.get('decimal_longitude'))

            LonB=float(gpsDataB.get('decimal_longitude'))

            LatA=float(gpsDataA.get('decimal_latitude'))

            LatB=float(gpsDataB.get('decimal_latitude'))

            tempsA=float(gpsDataA.get('fix_time'))

            tempsB=float(gpsDataB.get('fix_time'))

            speed =3.6*(3781009 + AltB+ abs(AltA - AltB) * (math.sqrt((abs(0.00007292115 * (math.radians(LonA- LonB)/(tempsA-tempsB)))) +(math.radians(LatA - LatB)/(tempsA-tempsB)) ** 2))

energie=0.5*masse/(3.6**2)*(speed ** 2 - speedA ** 2)

            print("vitesse = {}".format(speed))

print("Joules = {}".format(energie))

        speedA = speed

        gpsDataB=gpsDataA

Par produit en croix de Masse de la Terre => Rayon moyen de la Terre * vitesse angulaire de la rotation de la Terre

Masse de la Lune => Rayon moyen de la Lune * vitesse angulaire de la rotation de la Lune

On peut déterminer la masse de la Lune*(6371,009*7,292115*0,00001*3600)= 5,973 6 × 10²⁴ kg*1 737,4 km*2*PI/27,321 582/24

Masse de la Lune= 5,943117086*10^21Kg

Démonstration

Abeille butinant sur un brin de lavande

Abeille butinant sur un brin de lavande

synthèse additive sur un cylindre qui tourne avec blender

Cylindre déformé RVB

Produit matriciel	(1/2^n;1/2^n) où n est le degré d’optimisation
(Vitesse d’ouverture pour une synthèse additive d’un groupe de couleurs RVB; angle n*alpha avec n>0)	(Vitesse d’ouverture de l’appareil photo; angle alpha)

Soient θ = ωt et ω = 2$\pi$f, où θ est un angle en radians, f la fréquence de la platine en tours par minutes et t le temps en secondes.

• On fait correspondre ω = 2$\pi$f et ω = θ/t, d'où 2$\pi$f = θ/t.
• On simplifie : t = θ/(2$\pi$f).
• On convertit f en tours par seconde et on obtient t = θ/(2$\pi$f)/60), d'où : t = (60 $*$ θ)/(2$\pi$f).

pour n=0

Sur un disque tournant sur une platine, on obtient une vitesse d'ouverture de l'appareil photo de :

$Vitesse\ d'ouverture\ de\ l'appareil\ photo=(60\ *\ angle\ en\ radians)/(nombre\ de\ tours\ platine\ par\ minute\ *\ 2\pi )$

• 
  Rose en flou stroboscopique à l'arrêt
• 
  Rose en flou stroboscopique en rotation

• 
  Galaxie en flou stroboscopique disque à l'arrêt
• 
  Galaxie en flou stroboscopique disque en rotation

• 
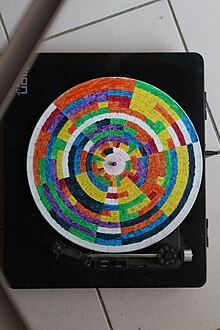
  Platine à l'arrêt
• 
  Platine en mouvement :
  78 tours/mn,
  vitesse d'ouverture 1/15 s,
  angle $\pi$/6

• 
  Sextuple spirale, réédition à l'arrêt
• 
  Sextuple spirale, réédition en mouvement

Table stroboscopique

angle	$\pi$/6	$\pi$/4	$\pi$/3	$\pi$/2	$\pi$	2$\pi$
33 tr/mn	0,1515151515	0,2272727273	0,303030303	0,4545454545	0,9090909091	1,8181818182
vitesse	1/6 s	1/5 s	0,3 s	0,5 s	1 s	2 s
45 tr/mn	0,1111111111	0,1666666667	0,2222222222	0,3333333333	0,6666666667	1,3333333333
vitesse	1/10 s	1/6 s	1/5s	0,3s	0,6s	1,3s
78 tr/mn	0,0641025641	0,0961538462	0,1282051282	0,1923076923	0,3846153846	0,7692307692
vitesse	1/15s	1/10s	1/8s	1/5s	0,4s	0,8s

Expériences

Disque de Newton à l'arrêt

Prisme à 2$\pi$

• 
  Modèle de disque de newton permuté
• 
  Disque de Newton permuté à $\pi$/7 pour chaque flou visible sur chaque flou visible Rouge Orange Jaune Vert Bleu Indigo Violet
• 
  Angle des couleurs flou visibles sur autre couleurs de flou visible

Et on obtient par un système de 6 équations à 7 inconnues pour chaque angle par rapport à une couleur :

Vert jaune orange rouge violet indigo bleu blanc 25 80 35 50 60 35 75 360 50 65 70 60 30 20 65 360 35 75 80 45 50 20 55 360 45 80 70 60 45 20 40 360 60 60 40 50 20 40 90 360 40 60 50 40 60 30 80 360 360 360 360 360 360 360 360 360

+ Vert = 4,200764818 + Jaune = 5,990439771 + Orange = –1,833652008 + Rouge = –2,728489484 + Violet = 0,575525813 + Indigo = –8,304015296 + Bleu = 3,099426386 Dégradé de flou de couleurs de base

Schémas optique d'une vue dans un champ visuel de PI/2 élargi 3 fois avec des miroirs

Dégradé linéaire d'après dégradé circulaire photographique

Disque de Newton en RVB

• 
  Disque aux couleurs de Newton
  en vue d'obtenir du blanc
• 
  Blanc du disque de Newton
  en spirale avec une lumière blanche
• 
  Violet du disque de Newton
  en spirale avec une lumière ultraviolette

• 
  Disque de Newton en RVB à l'arrêt
• 
  Angle de $\pi$/2, 33 tr/mn, flashé à 0,5 s
• 
  Angle de 2$\pi$, 33 tr/mn, flashé à 2 s

Synthèse additive

• 
  Table des couleurs
  en peinture acrylique
• Blanc UV synthèse additive RVB
• 
  Synthèse additive aux couleurs RVB
  sur un disque circulaire
• 
  Résultat de la synthèse additive
  45 tr/mn
  Angle de $\pi$/2
  flashé 0.3s

Produit Matriciel	(R/B)*Alpha* V/(R+V+B)	Alpha* V/(R+V+B)	(B/V)*Alpha* V/(R+V+B)
(Rouge; Vert; Bleu; angle Alpha)	Angle pour chaque valeur RVB différentes par dichotomie
ex Bleu roi (49;140;231; 45°)	5,25° de rouge	15° de vert	24,75° de bleu

méthode de coloriage par dichotomie

synthèse additive du coloriage par dichotomie 1/6s 45t pi/2

• 
  Synthèse additive
  flou stroboscopique 0
• 
  Synthèse additive
  flou stroboscopique $\pi$
• 
  Synthèse additive
  flou stroboscopique 2$\pi$
• Disque couleurs additives

En flou stroboscopique

En flou stroboscopique, on peut reproduire la synthèse additive avec un appareil photographique : c'est le phénomène de la lumière réfléchie comme de la lumière projetée sur un écran et surtout moins nocive pour la santé. On peut vérifier aussi la synthèse additive des couleurs sur le disque en le fixant sur un ventilateur, par exemple, où elle sera visible à vision humaine mais ne le sera pas sur une caméra.

Synthèse additive par lumière réfléchie sur un disque à 45 tr/mn	Couleurs sur un disque à l'arrêt pour une synthèse additive par lumière réfléchie

Diagramme de Venn des couleurs synthèse additive étendues

Gamme de gris

Disque synthèse additive étendue pour marron rose rouge vert

Disque synthèse additive étendue pour orange violet gris bleu

Disque synthèse additive étendue (cuivre, lavande, saumon et or)

• Diagramme de Venn des couleurs étendues de la synthèse additive par lumière réfléchie (survolez l'image)
• 
  Pour faire du gris anthracite, blanc crème et bleu maya
• 
  Gris anthracite, blanc crème et bleu maya

• Production du orange cassis et jaune par synthèse additive de lumière réfléchie
• 
  Partie 1
• 
  Partie 2

• Gamme de gris(gris anthracite,gris, gris souris, argent)
• 
  À l'arrêt
• 
  En mouvement

Théorie de l'absorption et de la réflexion de la lumière par les surfaces colorées

Vitraux	Fond gris	Nuancier stroboscopique sur fond chromatique	Stroboscopie de disque aux couleurs chromatiques

Flou stroboscopique sculpté

Modèle de flou stroboscopique sculpté	Flou stroboscopique sculpté

Flou cinétique radial

Stroboscopie à $\pi$/6	Retouche d'image faite à la main

Effet bras de levier

Dans le flou stroboscopique, l'effet bras de levier consiste, en diminuant l'angle de rotation avec une vitesse stroboscopique plus élevée, à éloigner du centre le flou vers l’extérieur et avoir un centre plus net.

• 
  Stroboscopie circulaire à 0,05 s
• 
  Stroboscopie circulaire à 0,033 s
• 
  Stroboscopie circulaire à 0,016 s
• 
  Stroboscopie circulaire à 0,00625 s
• 
  Stroboscopie circulaire à 0,0025 s

Le flou stroboscopique rectiligne

À plus grande échelle, le mouvement circulaire devient rectiligne et on obtient du flou stroboscopique rectiligne.

Ceci est la preuve que quel que soit la masse de la goutte d'eau en chute libre, un corps tombe à la même vitesse.

Stroboscopie rectiligne photographique à 0,005s

Retranscription du son par la couleur

When The Saints Go Marching In
Partition en spirale pour Flou Stroboscopique Chaque couleur représente une note selon sa longueur d'onde	Joué en Flou Stroboscopique en $\pi$/2 pour faire une mesure à 4 temps

• Le flou stroboscopique est un flou visible produit par l'effet d'un mouvement périodique d'un ou plusieurs points sur un disque capté lors de la prise de vue :

$Vitesse\ d'ouverture\ de\ l'appareil\ photo=(60\ *\ angle\ en\ radians)/(nombre\ de\ tours\ platine\ *\ 2\pi )$

Spirales sextuples, intervalle de 30° 6 couleurs peintes sur vinyle Platine à l'arrêt	78 tours pour obtenir un flou visible Vitesse d'ouverture photo : 1/15s	78 tours 30° 1/15s	78 tours 30° 1/15s

Vitraux sur fong gris pour flou stroboscopique	78tours 1/15s 30°	Stroboscopie à 1.3 et 45 tr/mn pour faire un tour complet soit 2$\pi$

• 
  Cascade
• 
  Flou stroboscopique fait main
  Made in France
• 
  Decopatch stroboscopique
• 
  Flou stroboscopique de poster

Photographie de Lewis W. Hine stroboscopiée à l'artisanale

Flou stroboscopique dans le sens horaire

Flou stroboscopique dans le sens horaire

Sonisphere

Disque original entre les mains du parquet de Paris Disque de Newston à l'arrêt

Stroboscopie du Disque de Newton à vitesse proche du 0 $\pi$

À vitesse proche du 2 $\pi$

Effet stroboscopique de My Way
Partition lumineuse Formatage en $\pi$/3 avec 8 octets sur 5 pistes	Jouée en 33 tr/mn Rotation de $\pi$/3 en 0,3 s

Effet stroboscopique du Boléro de Ravel Partition 10 secteurs de 12 octets sur 8 pistes Jouée en 78 tr/mn Prise à 1/13 s pour $\pi$/10

Effet stroboscopique du Smile (temps modernes) Partition de 72 secteurs de 4 noires sur 12 pistes Jouée en 33 tr/mn Angle $\pi$/3, 0,3 s

Bolerovideo

Effet stroboscopique de Swanee de Gershwin | Partition de 96 secteurs de 4 octets sur 6 pistes Jouée à $\pi$/4 Jouée à $\pi$/8

Effet stroboscopique de The entertainer de Scott Joplin 72 secteurs de 8 doubles croches sur 6 pistes Jouée en 33 tr/mn, $\pi$/6 et 1/6 s

Effet stroboscopique du French Cancan d'Offenbach 144 secteurs de 4 croches sur 12 pistes Jouée à 78 tr/mn, $\pi$/6 et 1/15 s

Effet stroboscopique de Lettre à Élise de Beethoven
90 secteurs de 6 doubles croches sur 15 pistes	78 tr/mn, $\pi$/3 et 1/8 s

Effet stroboscopique de la Marche de Radetzky de Johann Strauss 104 secteurs de 8 doubles croches,13 pistes Jouée à 78 tr/mn, $\pi$/4 et 1/10 s

Effet stroboscopique de Habanera de Carmen de Georges Bizet 88 secteurs sur 11 pistes 8 doubles croches Jouée à 45 tr/mn, $\pi$/4 et 1/6 s

Effet stroboscopique de Nocturne Op. n°2 de F. Chopin 36 sect., 12 pistes, 48 triples croches 78 tr/mn, 2$\pi$/3 et 1/4 s

Effet stroboscopique de La Marseillaise de Rouget de Lisle 40 secteurs 10 pistes 1/16 45 tr/mn, $\pi$/2 et 0.3 s

Effet stroboscopique de Pump and circumstance de Edward Elgar 80 secteurs 10 pistes 1/4 45 tr/mn, $\pi$/4 et 1.6 s

Lascia Ch'io Pianga de l'opéra Rinaldo de G. F. Händel
42 secteurs, 7 pistes, 1 croche	Joué en 45 tr/mn, $\pi$/3 et 1/5 s

El condor pasa 48 sect., 12 pistes, 16 dbles croches 78 tr/mn, $\pi$/2 et 1,5 s

Chicken Reel de Joseph M. Daly 52 secteurs 13 pistes 1 croche 78 tr/mn, $\pi$/2 et 1/5 s

L'apprenti sorcier de Paul Dukas 28 secteurs 7 pistes 3 croches 78 tr/mn, $\pi$/2 et 1/5 s

Valse n°2 de Dmitri Chostakovitch) 39 secteurs 13 pistes 12 dbles croches 78 tr/mn, 2$\pi$/3 et 1/4 s

Le beau Danube bleu de J. Strauss 345 secteurs 23 pistes 6 croches 33 tr/mn, 2$\pi$/15 et 1/8 s

Le Lac des Cygnes de P. I. Tchaikovsky 26 secteurs 13 pistes 8 croches 78 tr/mn, $\pi$ et 4 s

Camarada Hans Beimler de Ernst Busch 36 secteurs 12 pistes 8 croches 78 tr/mn, 2$\pi$/3 et 1/4 s

La truite de Franz Schubert 65 secteurs 13 pistes 1 dble croche 78 tr/mn, 2$\pi$/5 et 1/6 s

Toccata & Fugue en Ré mineur (Yasuo Sugiyama)
60 secteurs 12 pistes 16 dbles croches	45 tr/mn, 2$\pi$/5 et 1/4 s

La Marche turque de W. A. Mozart
1re partie		2ème partie
112 secteurs 14 pistes 8 dbles croches	78 tr/mn, $\pi$/8 et 1/20 s	112 secteurs 14 pistes 8 dbles croches	78 tr/mn, $\pi$/8 et 1/20 s

Hilarity Rag de James Scott
256 secteurs 32 pistes 1 double croche	45 tr/mn, $\pi$/4 et 1/6 s