Mesure en géométrie/Aire

Début de la boite de navigation du chapitre

fin de la boite de navigation du chapitre

Aire

Approche de la notion d'aire

Considérons une portion du plan délimitée par une figure fermée. L'aire est une valeur numérique habituellement notée A (plus souvent S en physique), et qui correspond à l'étendue de cette portion de plan. On parle également de surface ou de superficie.

On peut en donner une valeur approchée en découpant le plan en carrés de côté unité. Si l’on appelle n_i le nombre de carrés entièrement contenus dans la figure, et n_e le nombre minimum de carrés contenant entièrement la figure, alors son aire A est comprise entre n_i et n_e :

n_i ≤ A ≤ n_e.

Ou encore, si l’on doit carreler la portion de plan par des carreaux unité, l'aire est le nombre de carreaux qu’il faut utiliser. On voit ici que l'aire n’est pas nécessairement un nombre entier de carreaux unité (il faut faire des découpes) ; cela peut être un nombre rationnel, voire un nombre réel irrationnel.

Intuitivement, l'aire est souvent vue comme une sorte de nappe. Elle peut aussi être exprimée par des intervalles dans un espace vectoriel de dimension 2.

Aire de polygones courants

Carré d’un nombre et aire d’un carré

Définition

Si a est un nombre, le produit de a par lui-même s’appelle « carré de a » et se note :

a² = a × a

Propriété

Un carré de côté a a pour aire

A = a².

Exemple

L'aire d’un carré de côté 3 est 9 car 3² = 3 × 3 = 9.

L'aire d’un carré de côté 8 est 64 car 8² = 8 × 8 = 64

Aire d’un rectangle

L'aire d’un rectangle de longueur L et de largeur l vaut :

$A=L\times l$

On notera qu'un carré est un rectangle particulier, tel que L = l = a.

$L=l=a$

donc

$A=L\times l$

est

$A=a\times a$

ou

$A=a^{2}$

Aire d’un triangle

Triangle rectangle

Un triangle rectangle est la moitié d’un rectangle

Considérons un triangle rectangle dont les côtés de l'angle droit valent a et b. Alors, son aire A vaut :

$\mathrm {A} ={\frac {a\times b}{2}}$.

En effet, c’est la moitié d’un rectangle de dimensions a et b.

Triangle quelconque

Calcul de l'aire d’un triangle

L'aire A d’un triangle est égale à la moitié du produit de sa hauteur h et de sa base b :

$\mathrm {A} ={\frac {h\times b}{2}}$.

On peut le démontrer facilement à partir des aires des triangles rectangles mis en évidence sur la figure.

Aire d’un losange

Calcul de l'aire d’un losange

Soit un losange dont les diagonales ont pour longueur a et b. Son aire A est égale à la moitié du produit des longueurs des diagonales :

$\mathrm {A} ={\frac {a\times b}{2}}$.

En effet, on peut découper le losange et le réarranger pour en faire un rectangle de dimensions b et a/2.

Aire d’un trapèze

Découpage d’un trapèze pour le calcul de son aire

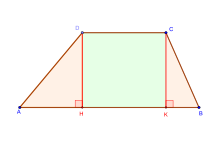
Soit un trapèze de petite base a, de grande base b et de hauteur h. Son aire A est égale au produit de la moyenne des bases et de la hauteur :

$\mathrm {A} ={\frac {a+b}{2}}\times h$.

On peut le démontrer en découpant le trapèze en un rectangle et deux triangles rectangles.

Aire d’un disque

L'aire A du disque de rayon a est π × a²

Un disque de rayon r a pour aire

$A=\pi r^{2}$.

Rappel

Le nombre π (pi) est une constante valant à peu près

π ≃ 3,141592654.