Début de la boite de navigation du chapitre
fin de la boite de navigation du chapitre
En raison de limitations techniques, la typographie souhaitable du titre, «
Mécanique du point : Oscillateurs Mécanique du point/Oscillateurs », n'a pu être restituée correctement ci-dessus.
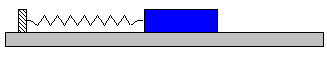
Mouvement horizontal On considère un mobile auto porteur relié à un mur par un ressort de raideur k.
Bilan des forces :
Une force de rappel
F
→
R
{\displaystyle {\vec {F}}_{R}}
Le poids
P
→
{\displaystyle {\vec {P}}}
La réaction du support
R
→
{\displaystyle {\vec {R}}}
On applique le principe fondamental de la dynamique au mobile :
m
a
→
=
F
→
R
+
P
→
+
R
→
{\displaystyle m\,{\vec {a}}={\vec {F}}_{R}+{\vec {P}}+{\vec {R}}}
On projette sur l'axe (Ox) :
m
x
¨
(
t
)
=
−
k
x
(
t
)
{\displaystyle m{\ddot {x}}(t)=-kx(t)}
On définie la pulsation propre de l'oscillateur :
ω
0
2
=
k
m
{\displaystyle \omega _{0}^{2}={\frac {k}{m}}}
On obtient une équation différentielle du second degré :
x
¨
+
ω
0
2
x
=
0
{\displaystyle {\ddot {x}}+\omega _{0}^{2}x=0}
Bilan des forces :
Poids
P
→
=
m
g
→
{\displaystyle {\vec {P}}=m{\vec {g}}}
Force de rappel du ressort :
F
→
R
=
−
k
(
l
−
l
0
)
u
→
x
{\displaystyle {\vec {F}}_{R}=-k(l-l_{0}){\vec {u}}_{x}}
Principe fondamental de la dynamique :
m
a
→
=
m
g
→
−
k
(
l
−
l
0
)
u
→
x
{\displaystyle m{\vec {a}}=m{\vec {g}}-k(l-l_{0}){\vec {u}}_{x}}
On projette sur l'axe à l'équilibre :
0
=
m
g
−
k
(
l
e
−
l
0
)
{\displaystyle 0=mg-k(l_{e}-l_{0})}
k
l
e
=
m
g
+
k
l
0
{\displaystyle kl_{e}=mg+kl_{0}}
l
e
=
l
0
+
m
g
k
{\displaystyle l_{e}=l_{0}+{mg \over k}}
On introduit x l'écart par rapport à la position d'équilibre :
l
=
l
e
+
x
{\displaystyle l=l_{e}+x}
m
x
¨
=
m
g
−
k
(
l
−
l
0
)
{\displaystyle m{\ddot {x}}=mg-k(l-l_{0})}
m
x
¨
=
m
g
−
k
(
l
e
+
x
−
l
0
)
{\displaystyle m{\ddot {x}}=mg-k(l_{e}+x-l_{0})}
m
x
¨
=
m
g
−
k
(
l
0
+
m
g
k
+
x
−
l
0
)
{\displaystyle m{\ddot {x}}=mg-k(l_{0}+{mg \over k}+x-l_{0})}
m
x
¨
=
m
g
−
k
l
0
−
m
g
−
k
x
+
k
l
0
{\displaystyle m{\ddot {x}}=mg-kl_{0}-mg-kx+kl_{0}}
m
x
¨
=
−
k
x
{\displaystyle m{\ddot {x}}=-kx}
x
¨
+
k
m
x
=
0
{\displaystyle {\ddot {x}}+{k \over m}x=0}
On cherche si une solution de la forme
x
(
t
)
=
A
sin
(
ω
0
t
+
ϕ
)
{\displaystyle x(t)=A\sin(\omega _{0}t+\phi )}
x
˙
(
t
)
=
d
x
(
t
)
d
t
=
A
ω
0
c
o
s
(
ω
0
t
+
ϕ
)
{\displaystyle {\dot {x}}(t)={\frac {dx(t)}{dt}}=A\omega _{0}cos(\omega _{0}t+\phi )}
x
¨
(
t
)
=
d
2
x
(
t
)
d
t
2
=
−
A
ω
0
2
sin
(
ω
0
t
+
ϕ
)
=
−
ω
0
2
x
(
t
)
{\displaystyle {\ddot {x}}(t)={\frac {d^{2}x(t)}{dt^{2}}}=-A\omega _{0}^{2}\sin(\omega _{0}t+\phi )=-\omega _{0}^{2}x(t)}
Introduisons ces expressions dans la partie gauche de l'équation caractéristique :
x
¨
(
t
)
+
ω
0
2
x
(
t
)
=
−
ω
0
2
x
(
t
)
+
ω
0
2
x
(
t
)
=
0
{\displaystyle {\begin{aligned}{\ddot {x}}(t)+\omega _{0}^{2}x(t)&=-\omega _{0}^{2}x(t)+\omega _{0}^{2}x(t)\\&=0\end{aligned}}}
A est l'amplitude (en mètre) et
ϕ
{\displaystyle \phi }
La période propre
T
0
{\displaystyle T_{0}}
2
π
{\displaystyle 2\pi }
ω
0
T
0
=
2
π
{\displaystyle \omega _{0}T_{0}=2\pi }
Ainsi :
T
0
=
2
π
ω
0
=
2
π
m
k
{\displaystyle T_{0}={2\pi \over \omega _{0}}=2\pi {\sqrt {m \over k}}}
La période est indépendante de l'amplitude du mouvement. Un tel système est dit isochrone .
La vitesse est :
v
=
x
˙
(
t
)
=
A
ω
c
o
s
(
ω
0
t
+
ϕ
)
{\displaystyle v={\dot {x}}(t)=A\omega cos(\omega _{0}t+\phi )}
L'énergie cinétique est :
E
c
=
1
2
m
v
2
=
1
2
m
A
2
ω
0
2
c
o
s
2
(
ω
0
t
+
ϕ
)
=
1
2
k
A
2
c
o
s
2
(
ω
0
t
+
ϕ
)
{\displaystyle E_{c}={1 \over 2}mv^{2}={1 \over 2}mA^{2}\omega _{0}^{2}cos^{2}(\omega _{0}t+\phi )={1 \over 2}kA^{2}cos^{2}(\omega _{0}t+\phi )}
L'énergie potentielle est :
E
p
=
1
2
k
x
2
=
1
2
k
A
2
s
i
n
2
(
ω
0
t
+
ϕ
)
{\displaystyle E_{p}={1 \over 2}kx^{2}={1 \over 2}kA^{2}sin^{2}(\omega _{0}t+\phi )}
L'énergie mécanique est :
E
m
=
E
c
+
E
p
=
1
2
k
A
2
(
c
o
s
2
(
ω
0
t
+
ϕ
)
+
s
i
n
2
(
ω
0
t
+
ϕ
)
)
=
1
2
k
A
2
{\displaystyle E_{m}=E_{c}+E_{p}={1 \over 2}kA^{2}(cos^{2}(\omega _{0}t+\phi )+sin^{2}(\omega _{0}t+\phi ))={1 \over 2}kA^{2}}
L'énergie mécanique est constante au cours du temps et proportionnelle au carré de l'amplitude.
θ
¨
+
ω
0
2
θ
=
0
{\displaystyle {\ddot {\theta }}+\omega _{0}^{2}\theta =0}
ω
0
2
=
g
l
{\displaystyle \omega _{0}^{2}={\frac {g}{l}}}
En plus de la force de rappel, la particule est soumise à une force de frottement F=-bv. On applique le principe fondamental de la dynamique :
m
x
¨
=
−
b
x
˙
−
k
x
{\displaystyle m{\ddot {x}}=-b{\dot {x}}-kx}
m
x
¨
+
b
x
˙
+
k
x
=
0
{\displaystyle m{\ddot {x}}+b{\dot {x}}+kx=0}
x
¨
+
2
β
x
˙
+
ω
0
2
x
=
0
{\displaystyle {\ddot {x}}+2\beta {\dot {x}}+\omega _{0}^{2}x=0}
ω
0
2
=
k
m
{\displaystyle \omega _{0}^{2}={k \over m}}
2
β
=
b
m
{\displaystyle 2\beta ={b \over m}}
Le discriminant est :
δ
=
4
β
2
−
4
ω
0
2
=
4
(
β
2
−
ω
0
2
)
{\displaystyle \delta =4\beta ^{2}-4\omega _{0}^{2}=4(\beta ^{2}-\omega _{0}^{2})}
δ
=
2
β
2
−
ω
0
2
{\displaystyle {\sqrt {\delta }}=2{\sqrt {\beta ^{2}-\omega _{0}^{2}}}}
Les solutions sont :
x
1
=
−
2
β
−
2
δ
2
=
−
β
−
β
2
−
ω
0
2
{\displaystyle x_{1}={-2\beta -2{\sqrt {\delta }} \over 2}=-\beta -{\sqrt {\beta ^{2}-\omega _{0}^{2}}}}
x
2
=
−
2
β
+
2
δ
2
=
−
β
+
β
2
−
ω
0
2
{\displaystyle x_{2}={-2\beta +2{\sqrt {\delta }} \over 2}=-\beta +{\sqrt {\beta ^{2}-\omega _{0}^{2}}}}
M
x
¨
+
B
x
˙
+
K
x
=
F
cos
ω
t
{\displaystyle M{\ddot {x}}+B{\dot {x}}+Kx=F\cos \omega t}