Limites d'une fonction/Annexe/Limite en zéro : approche expérimentale
Une page de Wikiversité.
 |
|||
| Annexe | |||
| Leçon : Limites d'une fonction |
|---|
En raison de limitations techniques, la typographie souhaitable du titre, « Limites d'une fonction — Annexe : Limite en zéro : approche expérimentale
Limites d'une fonction/Annexe/Limite en zéro : approche expérimentale », n'a pu être restituée correctement ci-dessus.
[modifier] Limite d'une fonction naturellement définie en zéro
Soit la fonction ƒ définie sur 
par pour tout 
1. Remplir le tableau suivant :
2. Si ƒ(x) s'approche de plus en plus près d'une valeur L quand x s'approche de zéro, on dit que ƒ tend vers L quand x tend vers zéro, ou que ƒ a pour limite L en zéro. Cela se note 
Quel est un bon candidat pour 
dans notre exemple ?
1. Remplir le tableau suivant :
2. On peut conjecturer que, dans notre cas, 
On pourrait croire que calculer la limite en zéro revient à remplacer x par 0 dans la formule qui donne f(x), c'est-à-dire calculer f(0).
Mais le problème de la limite d'une fonction en zéro se pose surtout lorsque cette fonction est bien définie « autour » de zéro par une formule algébrique, mais que cette formule n'est pas valable pour x = 0.
[modifier] Limite d'une fonction non définie en zéro
Soit la fonction ƒ définie par, pour 
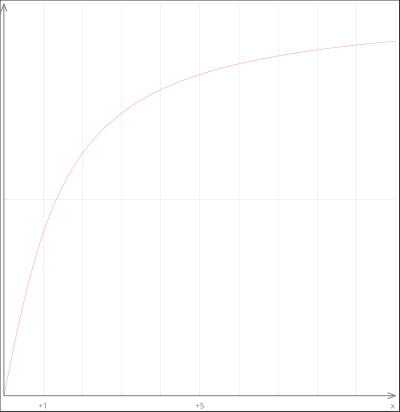
1. Expliquer pourquoi ƒ n'est pas définie en 0.
2. Tracer la courbe de ƒ.
3. Remplir le tableau suivant :
Quel est un bon candidat pour dans notre exemple ?
1. On ne peut pas diviser par 0 car x est au dénominateur.
2. 
3. 
[modifier] Exercice
Trouver dans les 3 cas suivants par expérimentation sur la calculatrice.
1. 
2. 
3. 
1. 
2. 
3. 
